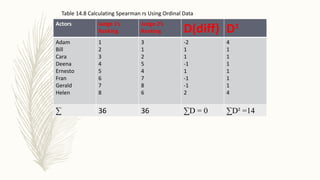
This document discusses the Spearman rank order correlation coefficient, which is used to examine the association between two ordinally scaled variables when the relationship is not linear. It provides an example of calculating Spearman's rs using rankings of actors by two judges. The rs value of 0.83 is greater than the critical value of 0.738 for the sample size, so the null hypothesis of no difference is rejected.

1. The Spearman
Rank Order
Correlation
Coefficient
Desmond Ayim-Aboagye,
PhD
Association between two ordinally
scaled variables

2. The Spearman is also Pearson r
formula to rank-ordered data
– The Spearman rank order correlation coefficient, is used to examine the nature
of association found between two ordinally scaled variables.
– It is symbolized rs (occasionally p, or “rho”).

3. Difference
– The Pearson r is ideal for
measuring associations that are
linear (e.g., as X increases in value,
a corresponding increase in Y
occurs)
– The Spearman rs, when the
relationship is not linear.

4. Actors Judge 1’s
Ranking
Judge 2’s
Ranking D(diff) D²
Adam
Bill
Cara
Deena
Ernesto
Fran
Gerald
Helen
1
2
3
4
5
6
7
8
3
1
2
5
4
7
8
6
-2
1
1
-1
1
-1
-1
2
4
1
1
1
1
1
1
4
∑ 36 36 ∑D = 0 ∑D² =14
Table 14.8 Calculating Spearman rs Using Ordinal Data

5. Formula for Spearman rs:
Rs = 1-
6∑𝐷²
𝑁(𝑁2−1)

6. Calculating
– Rs = 1-
6∑𝐷²
𝑁(𝑁2−1)
– Rs = 1-
6(14)
8[ 82−1 ]
– Rs = 1-
84
8(64−1)
– Rs = 1-
84
8(63)
– Rs = 1-
84
504
– Rs = 1- .1667
– Rs = .83.

7. Rejecting or accepting
Hypothesis
– Table B. 10 in Appendix B
– As usual we perform a two-tailed test at the 0.05 level
– So we read the row for N = 8 [sample size] and locate the critical value of .738
– Is the observed rs of .83 greater than or equal to the rs critical value of .738.
Yes we can reject the null hypothesis of no difference, or:
– rs (8) = .83 ≥ rs critical (8) = .738; Reject H0.