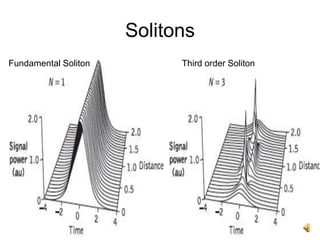
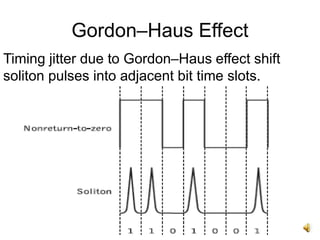
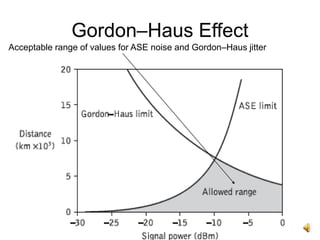
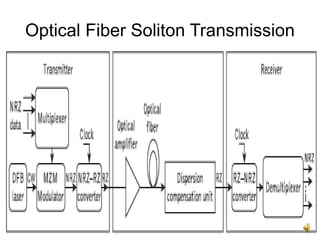
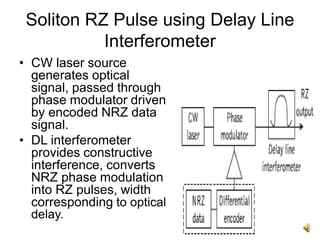
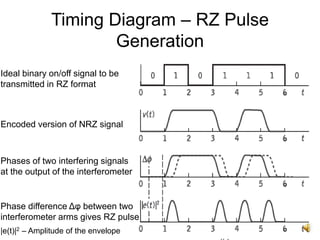
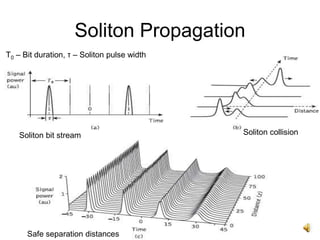
The document discusses soliton systems in optical fiber transmission, highlighting the properties of solitons, such as self-maintaining shape and collision invariance. It details the Gordon-Haus effect, which introduces timing jitter that impacts soliton transmission efficiency, requiring careful noise management for long distances. The document also covers the technical aspects of generating and propagating soliton pulses, including modulation techniques and the implications of dispersion and attenuation in high-speed fiber systems.