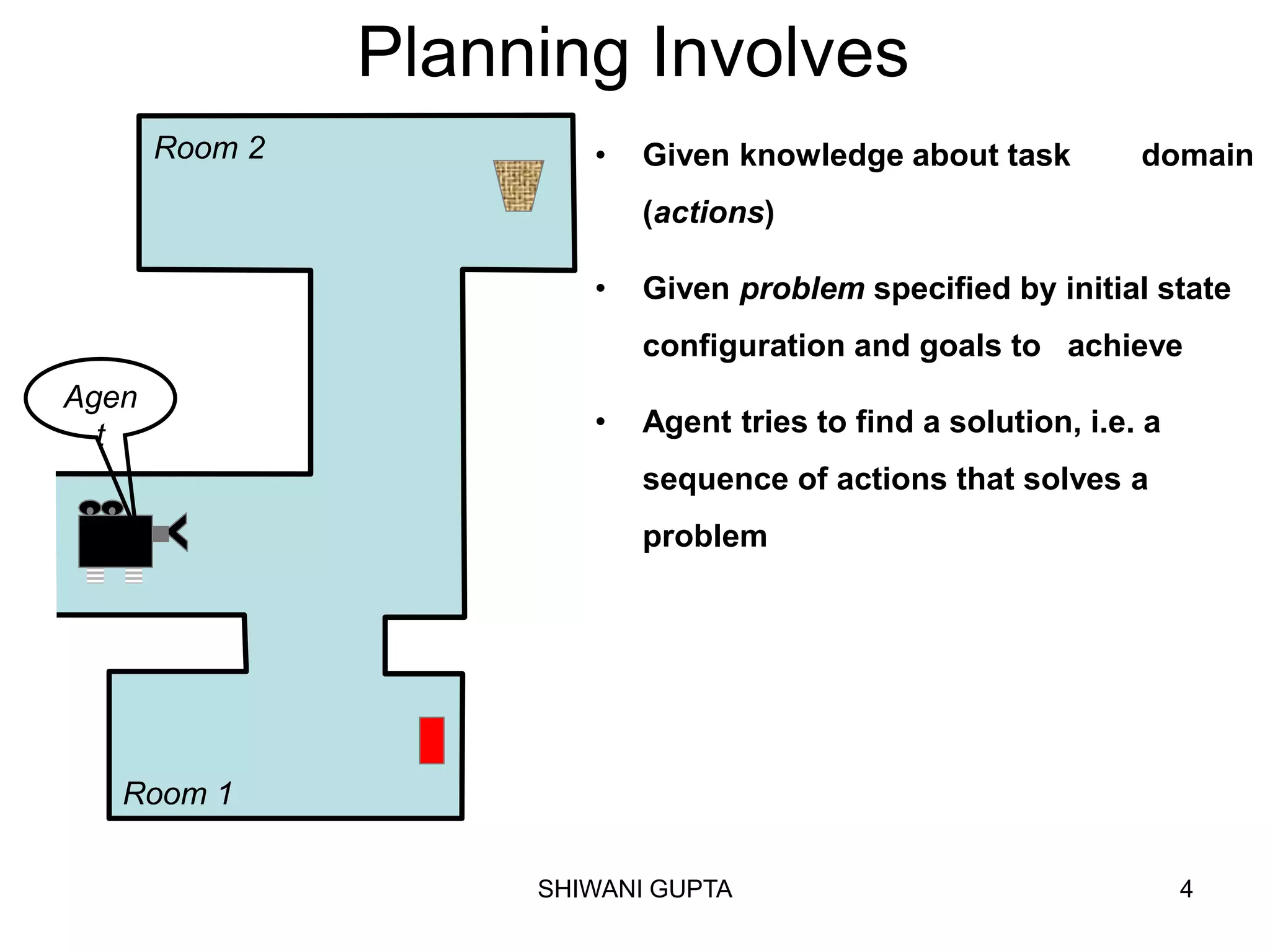
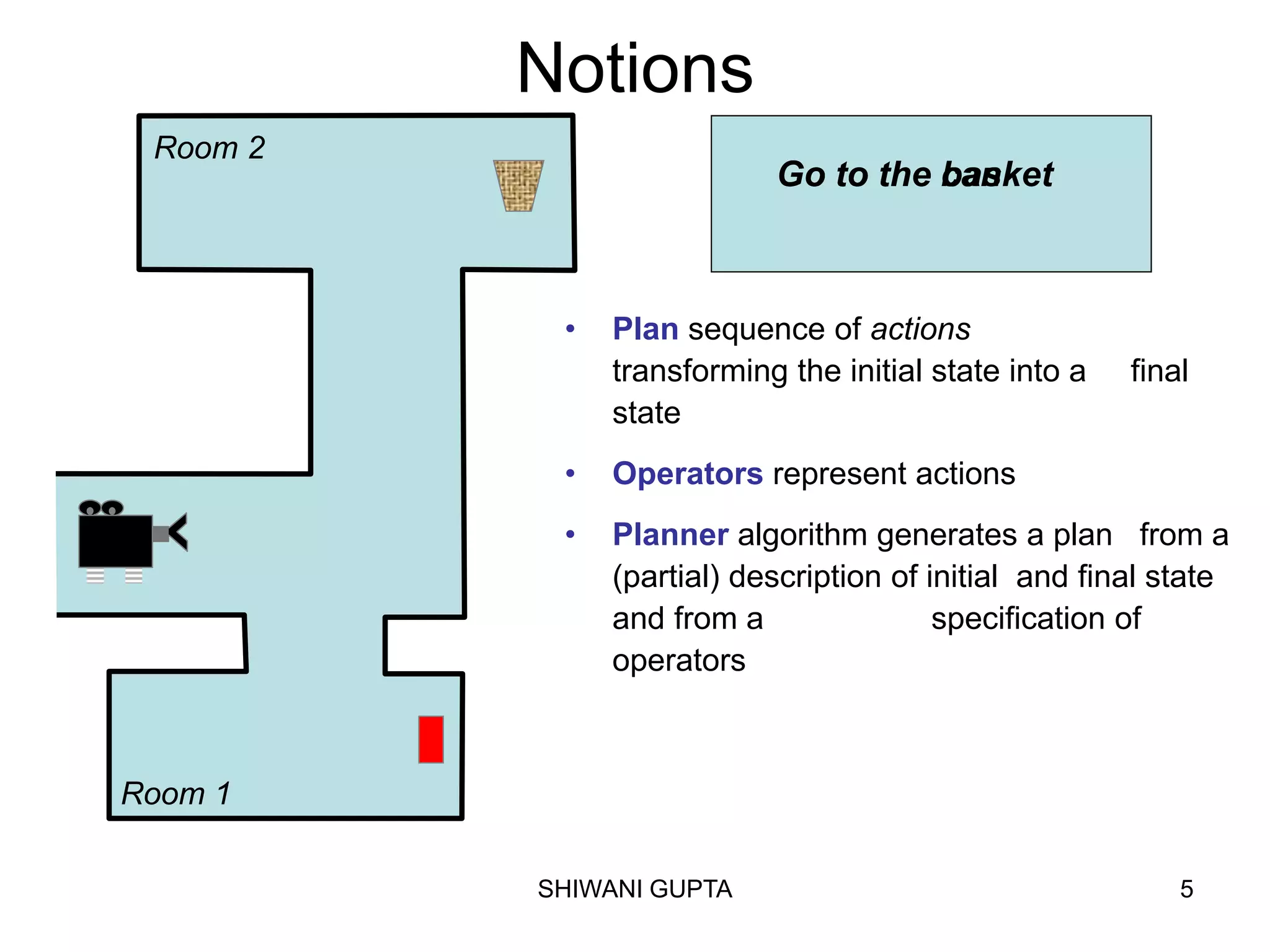
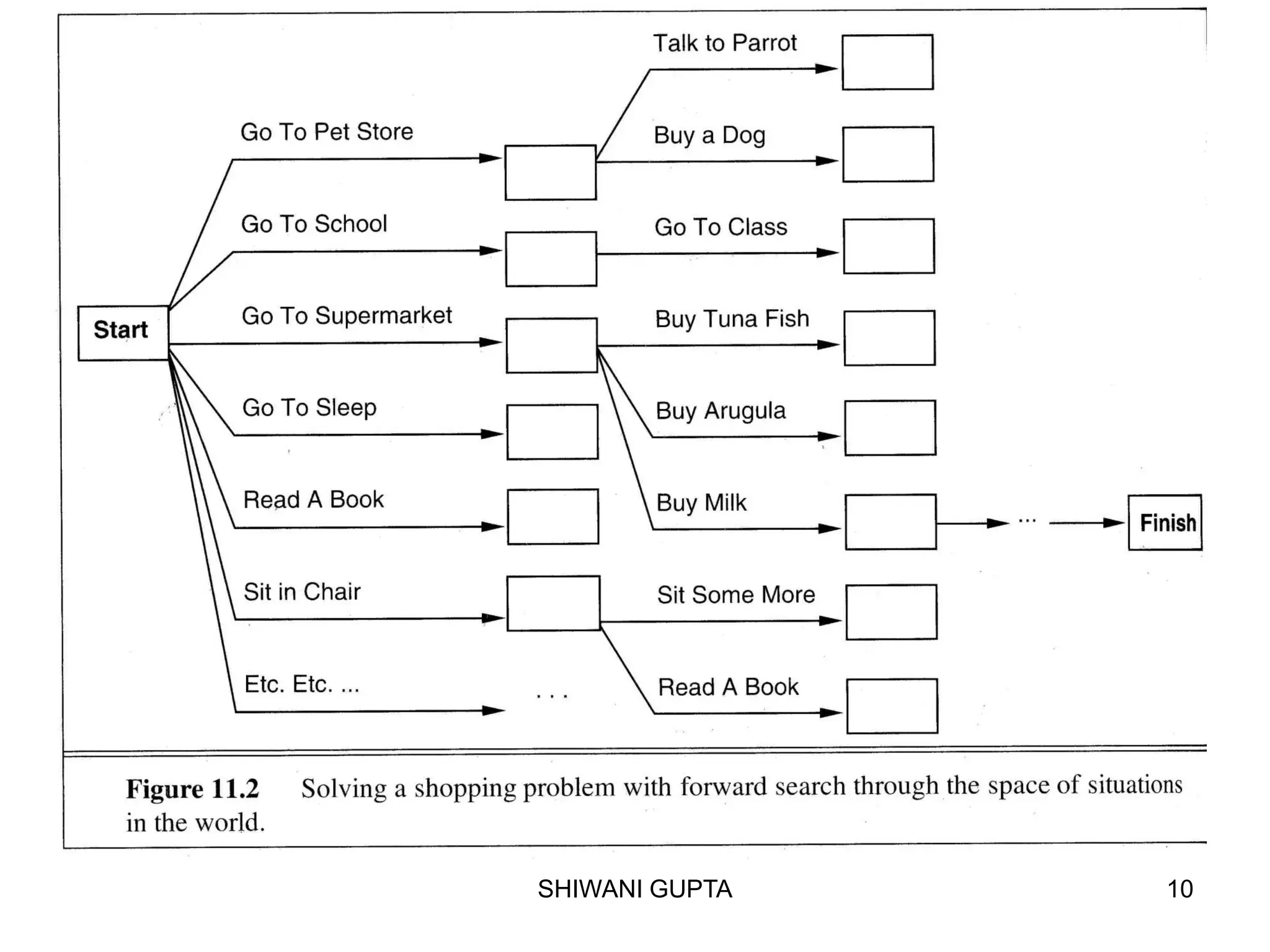
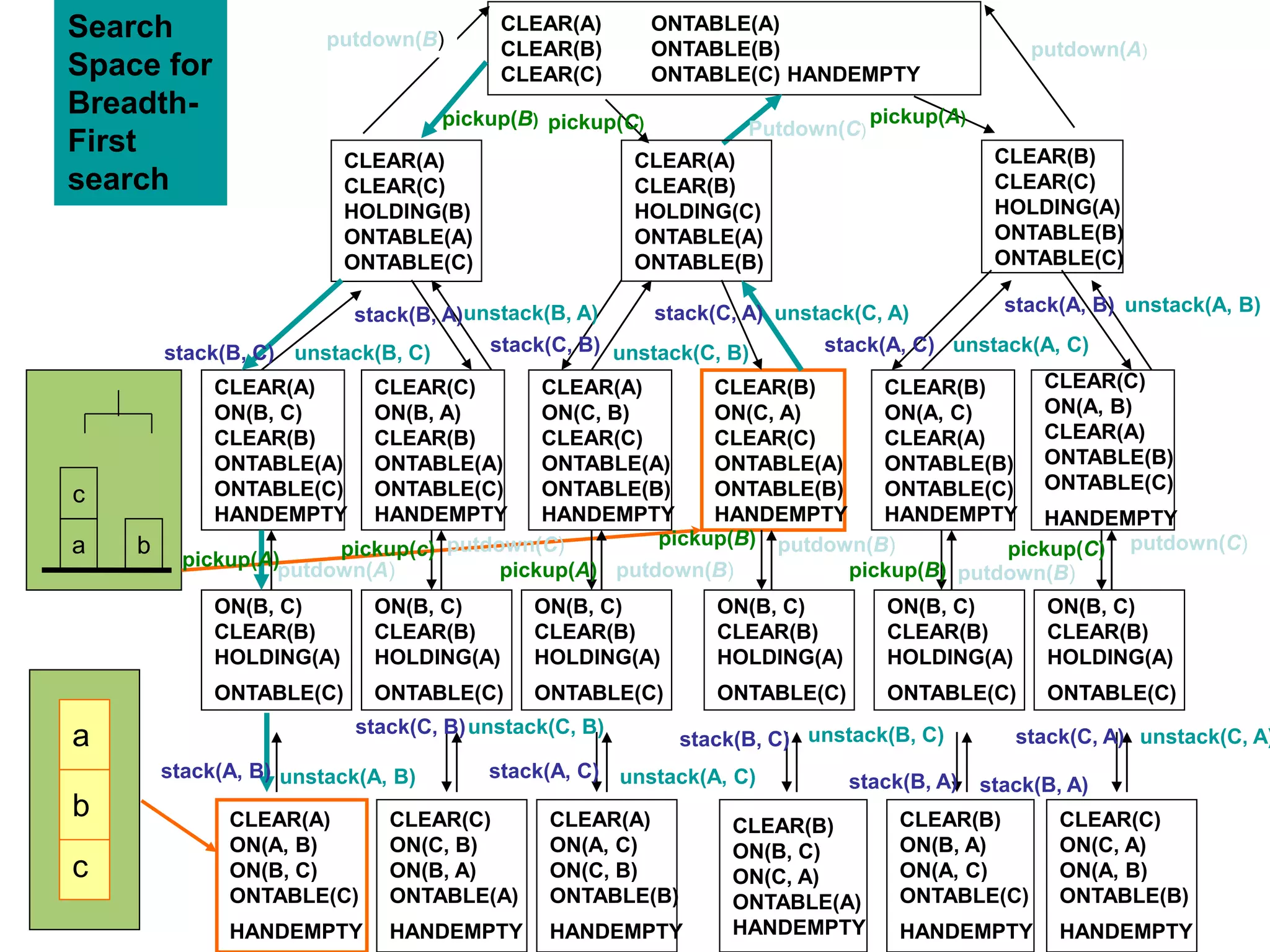
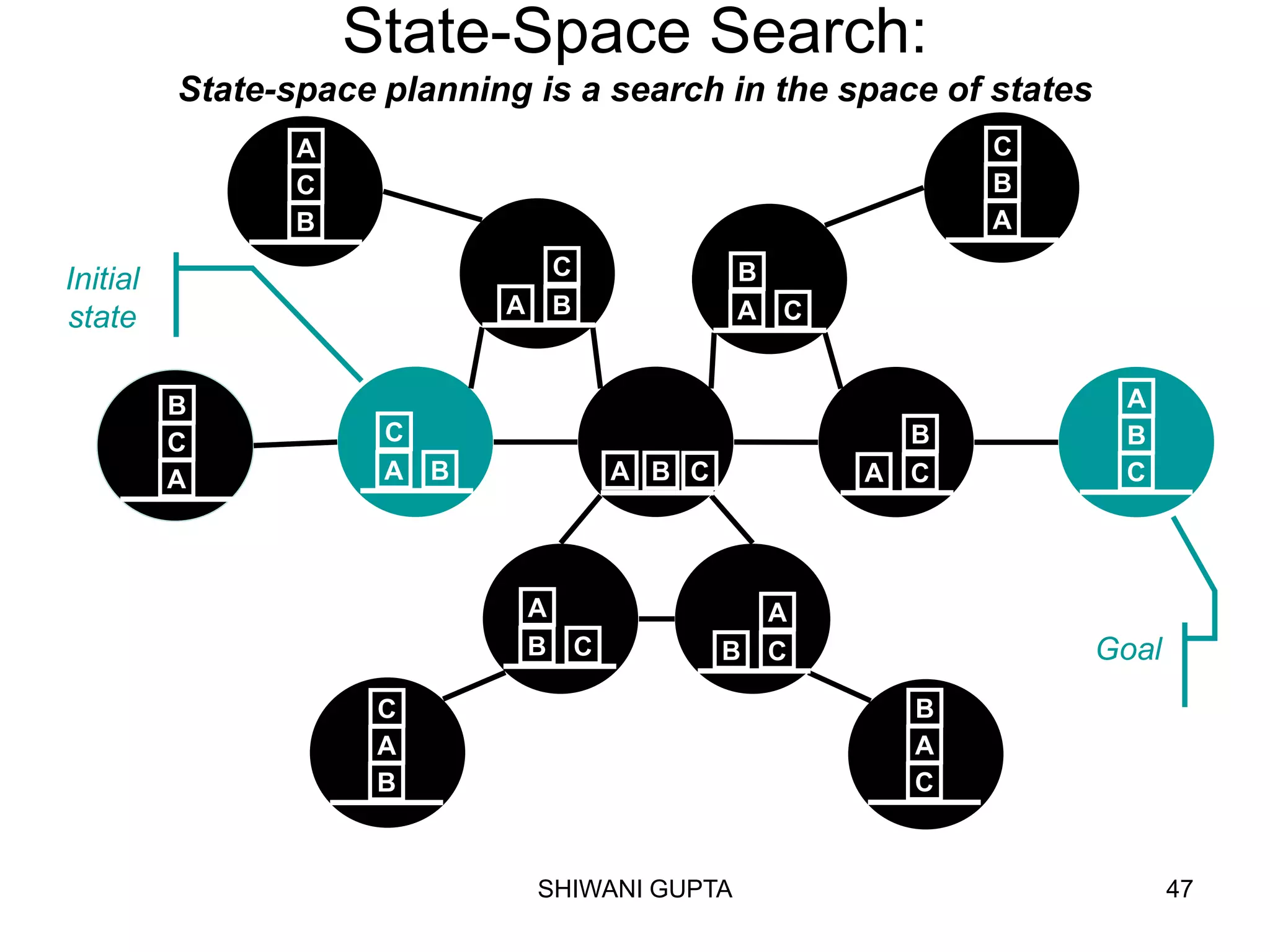
Planning involves representing an initial state, possible actions, and a goal state. A planning agent uses a knowledge base to select action sequences that transform the initial state into a goal state. STRIPS is a common planning representation that uses predicates to describe states and logical operators to represent actions and their effects. A STRIPS planning problem specifies the initial state, goal conditions, and set of operators. A solution is a sequence of ground operator instances that produces the goal state from the initial state.

1. PART V
PLANNING and LEARNING

2. PLANNING
The planning problem
Planning with state space search
Partial order planning
Hierarchical planning
Conditional Planning

3. SHIWANI GUPTA 3
Example application areas
Proof Planning
in Mathematics
Speech and
Dialog Planning
Design and
Manufacturing
Military operations
and logistics
Games
Space exploration

4. SHIWANI GUPTA 4
Planning Involves
• Given knowledge about task domain
(actions)
• Given problem specified by initial state
configuration and goals to achieve
• Agent tries to find a solution, i.e. a
sequence of actions that solves a
problem
Room 2
Room 1
Agen
t

5. SHIWANI GUPTA 5
Go to the basketGo to the can
Notions
• Plan sequence of actions
transforming the initial state into a final
state
• Operators represent actions
• Planner algorithm generates a plan from a
(partial) description of initial and final state
and from a specification of
operators
Room 2
Room 1

6. SHIWANI GUPTA 6
Planning Agent =
Problem Solving Agent + Knowledge Based
agent
(Generate sequences of actions to perform tasks and achieve
objectives)
Problem Solving agent:-to consider the
consequences of sequences of actions before
acting.
Knowledge Base Agent:-can select actions based
on explicit logical representations of the current
state and the effects of actions.
A SIMPLE PLANNING AGENT
1. Generate a goal to achieve
2. Construct a plan to achieve goal from current state

7. SHIWANI GUPTA 7

8. SHIWANI GUPTA 8

9. SHIWANI GUPTA 9
Basic elements of problem-solving
– representation of actions
– representation of states
– representation of goals
– representation of plans
Example: Shopping problem
“Get a quart of milk, a bunch of banana
and a variable-speed cordless drill”
• need to define
– initial state
– operations

10. SHIWANI GUPTA 10

11. SHIWANI GUPTA 11
• Problem solver in Figure above
– too many branches
– too many actions, states
– heuristic evaluation function
• Problem-Solving agent
– consider sequence of actions from the initial state
– decide what to do in the initial state when given relevant choices
– it cannot decide where to go until the agent figures out how to
obtain items
• Planning agent
– “Open up” the representation of states, goals and actions
states and goals : sets of sentences
actions : logical description of precondition and effects
direct connections between states and actions
eg. goal : conjunction Have(Milk)  Buy(x)
– “free” to add actions
– most goals of the world are independent of most other parts
divide-and-conquer strategy

12. SHIWANI GUPTA 12
Planning in Situation Calculus
A planning problem represented in situation calculus by logical
sentences
– initial state: For shopping problem
At(Home,s0)  ¬Have(Milk, s0)  ¬Have(Banana, s0) 
¬Have(Drill,s)
– goal state: a logical query
s At(Home,s)  Have(Milk,s)  Have(Bananas,s) 
Have(Drill,s)
– operators: description of actions
a,s Have(Milk,Result(a,s))  [(a=Buy(Milk) 
At(Supermarket,s)  (Have(Milk,s)  a  Drop(Milk))]
Result’(l,s) means result from sequence of actions starting in
s.
s Result’([],s)=s

13. SHIWANI GUPTA 13
• A solution to the shopping problem is a plan P
So, yields a situation satisfying the goal query :
At(Home, Result’(P,s0))  Have(Milk,Result’(P, s0)) 
Have(Bananas, Result’(P, s0)  Have(Drill,Result’ (P, s0))
P=[Go(Supermarket), Buy(Bananas), Go(HardwareStore), Buy(Drill),
Go(Home)]
• To make planning practical
(1) Restrict the language
(2) use a special-purpose algorithm

14. SHIWANI GUPTA 14
Basic Representations for planning
• STRIPS (Stanford Research Institute Problem Solver):
Representation for state and goals
– initial state for the shopping problem
At(Home)  ¬Have(Milk)  ¬Have(Banana)  ¬Have(Drill) 
…… incomplete state description
– goal
At(Home)  Have(Milk)  Have(Banana)  Have(Drill)
It can contain variables At(x)  Sells(x,Milk)
The initial and goal state are input to planning systems

15. SHIWANI GUPTA 15
Representation for actions
STRIP operations consist of
action description
precondition
effect/post condition
eg. Op(ACTION:Go(there),
PRECOND:At(here)  Path(here,there),
EFFECT:At(there)  ¬At(here))

16. SHIWANI GUPTA 16
Situation space and plan space
Situation space
• progression planner : forward search
• regression planner : backward search
expand it with a complete plan that solves the problem  plan space
Refinement operators take a partial plan and add constraints to it
Search through the space of situations and Search through the space of
plans
Representation for plans
– To search through a space of plans eg. “putting on a pair of shoes”
– goal : RightShoeOn  LeftShoeOn
– initial state : no literal
– operators:
Op(ACTION:RightShoe,PRECOND:RightSockOn,EFF
ECT:RightShoeOn)
Op(ACTION:RightSock,EFFECT:RightSockOn)

17. SHIWANI GUPTA 17
• A plan is defined as a data structure
– A set of plan steps
– A set of step ordering
– A set of variable binding constraints
– A set of causal links : si
c sj ”precondition c of sj is achieved
by si”
• initial plan before any refinements
Start < Finish
Refine and manipulate until a plan that is a solution- Initial plan

18. SHIWANI GUPTA 18

19. SHIWANI GUPTA 19

20. SHIWANI GUPTA 20
Solutions
– solution : a plan that an agent guarantees goal
achievement
– a solution is a complete and consistent plan
– a complete plan : every precondition of every step
is achieved by some other step
– a consistent plan : no contradictions in the
ordering or binding constraints.
When we meet a inconsistent plan we backtrack and
try another branch

21. SHIWANI GUPTA 21
A partial-order planning example
Shopping problem: “get milk, banana, drill and bring them back
home”
– assumption
1)Go action can travel the two locations
2)no need money
– initial state : operator start
Op(ACTION:Start, EFFECT:At(Home)  Sells(HWS,Drill) 
Sells(SM,Milk), Sells(SM,Banana))
– goal state : Finish
Op(ACTION:Finish, PRECOND:Have(Drill)  Have(Milk) 
Have(Banana)  At(Home))
– actions:
Op(ACTION:Go(there), PRECOND:At(here),
EFFECT:At(there)  ¬At(here))
Op(ACTION:Buy(x), PRECOND:At(store)Sells(store,x),
EFFECT:Have(x))

22. SHIWANI GUPTA 22
• There are many possible ways in which the initial plan is
elaborated
– one choice : three Buy actions for three preconditions of
Finish action
– second choice : sells precondition of Buy
• Bold arrows : causal links, protection of precondition
• Light arrows : ordering constraints

23. SHIWANI GUPTA 23

24. SHIWANI GUPTA 24
• causal links : protected links
a causal link is protected by ensuring that threats are ordered to
come before or after the protected link
• demotion : placed before
promotion : placed after

25. SHIWANI GUPTA 25

26. SHIWANI GUPTA 26

27. SHIWANI GUPTA 27
Partial-order planning algorithm

28. SHIWANI GUPTA 28
knowledge engineering for
planning
Methodology for solving problems with the
planning approach
(1) Decide what to talk about
(2) Decide on a vocabulary of conditions,
operators, objects
(3) Encode operators for the domain
(4) Encode a description of the specific problem
instance
(5) Pose problems to the planner and get back
plans

29. SHIWANI GUPTA 29
Planning in the Blocks World

30. SHIWANI GUPTA 30
eg. The blocks world
(1) What to talk about
• cubic blocks sitting on a table
• one block on top of another
• A robot arm picks up a block and moves it to another position
(2) Vocabulary
• objects: blocks and table
• On(b,x) : b is on x
• Move(b,x,y) : move b from x to y
• ¬  x On(x,b) or x ¬On(x,b) : precondition
• clear(x)
(3) Operators
Op(ACTION:Move(b,x,y),
PRECOND:On(b,x)  Clear(b)  Clear(y),
EFFECT:On(b,y)  Clear(x)  ¬On(b,x) 
¬Clear(y))
Op(ACTION:MoveToTable(b,x),

31. SHIWANI GUPTA 31
START
STATE

32. SHIWANI GUPTA 32
GOAL
STATE

33. SHIWANI GUPTA 33
The classical
Action
Procedures

34. SHIWANI GUPTA 34
Final triangular
Representation
of a Plan

35. SHIWANI GUPTA 35
What is a Planning Problem?
A planning problem is given by:
an initial state and a goal state.
B
D
A
C
Ontable (B)
Ontable (C)
On (D,B)
On (A,D)
Clear (A)
Clear (C)
Handempty
For a transition there are certain operators available.
PICKUP (x) picking up x from the table
PUTDOWN (x) putting down x on the table
STACK (x, y) putting x on y
UNSTACK (x, y) picking up x from y
→ in blocks world
- Formalise Operators!
- Find a plan!
GOAL:

36. SHIWANI GUPTA 36
STRIPS Domain Descriptions
• Planning problem:
– Initial state, goal conditions, set of operators
• Solution:
– A sequence of ground operator instances that produces the
goal from the initial state
• STRIPS Assumption: literals not mentioned remain
unchanged.
( The Frame Problem )

37. SHIWANI GUPTA 37
The “Frame Problem“
• One of the earliest solutions to the frame
problem was the STRIPS planning algorithm
– Specialized planning algorithm rather than general
purpose theorem prover
– Leaves facts unchanged from one state to the next
unless a planning operator explicitly changes them
Need to describe both what changes and what doesn‘t change

38. SHIWANI GUPTA 38
STRIPS Language (without negation)
• A subset of first-order logic:
- predicate symbols (chosen for the particular domain)
- constant symbols (chosen for the particular domain)
- variable symbols
- no function symbols!
• Atom: expression p(t1, ..., tn)
- p is a predicate symbol
- each t1 is a term

39. SHIWANI GUPTA 39
STRIPS Language (with negation)
• Literal: Is an atom p(t1, ..., tn), called a positive literal
or a negated atom ~ p(t1, ..., tn), called a negative literal
• A conjunct is represented either by a comma or a 
p1(t1, ..., tn), ~ p2(t1, ..., tn), p3(t1, ..., tn)
• For now, we won’t have any disjunctions, implications, or
quantifiers

40. SHIWANI GUPTA 40
Representing States of the World
• State: a consistent assignment of TRUE or FALSE to every
literal in the universe
• State description:
- a set of ground literals that are all taken to be TRUE
Note: in standard STRIPS, a state is restricted to contain only positive literals
a
c
b
on(c,a),ontable(a),clear(c),
ontable(b),clear(b),handempty
➢ The negation of these literals are taken to be false
➢ Truth values of other ground literals are unknown

41. SHIWANI GUPTA 41
STRIPS Operators (with negation)
• A STRIPS operator :
name(v1, v2, ..., vn)
Preconditions: atom1, atom2, ..., atomn
Effects: literal1, literal2, ..., literalm
unstack(?x,?y)
Preconditions: on(?x,?y), clear(?x), handempty
Effects: ~on(?x,?y), ~clear(?x), ~handempty,
holding(?x), clear(?y)
Operator Instance: replacement of variables by constants
Example:

42. SHIWANI GUPTA 42
cc
STRIPS Operators
• If all preconditions of a ground instance are true
(i.e., they occur) in a state description S, then O is applicable to
S
• Applying O to S produces the successor state description:
Result(S,O) = (S – Del(O))  Effects(O)
unstack(c,a)
Preconditions: on(c,a), clear(c), handempty
Effects: ~on(c,a), ~clear(c), ~handempty,
holding(c), clear(a)
on(c,a), ontable(a), clear(c),
ontable(b), clear(b),handempty
ontable(a), ontable(b), clear(b), ~on(c,a),
~clear(c), ~handempty, holding(c), clear(a)
ba
• Ground instance: replace all variables by
constantsunstack(c,a)
Preconditions: on(c,a), clear(c), handempty
Effects: ~on(c,a), ~clear(c), ~handempty,
holding(c), clear(a)

43. SHIWANI GUPTA 43
Example: The Blocks World
unstack(?x,?y)
Pre: on(?x,?y), clear(?x), handempty
Eff: ~on(?x,?y), ~clear(?x), ~handempty,
holding(?x), clear(?y)
stack(?x,?y)
Pre: holding(?x), clear(?y)
Eff: ~holding(?x), ~clear(?y),
on(?x,?y), clear(?x), handempty
pickup(?x)
Pre: ontable(?x), clear(?x), handempty
Eff: ~ontable(?x), ~clear(?x),
~handempty, holding(?x)
putdown(?x)
Pre: holding(?x)
Eff: ~holding(?x), ontable(?x),
clear(?x), handempty
b b
b
a
c
b
a
c
b
b b
b
a
c
b
a b
c
b b
b
a
c
b

44. SHIWANI GUPTA 44
STRIPS Operators: alternative
Formulation without Negation
• States contain only atoms
(positive literals)
• STRIPS operators use a
delete list instead of negated effects
name(v1, ..., vn)
Pre: atom, ..., atom
Add: atom, ..., atom
Del: atom, ..., atom
unstack(?x,?y)
Pre: on(?x,?y), clear(?x), handempty
Del: on(?x,?y), clear(?x), handempty,
Add: holding(?x), clear(?y)
a
c
b
on(c,a), ontable(a)
clear(c), ontable(b)
clear(b), handempty()

45. SHIWANI GUPTA 45
STRIPS Operators (alternative Formulation)
• If O is applicable to S, then
result(S,O) = (S - Del(O))  Add(O)
on(c,a), ontable(a), clear(c),
ontable(b), clear(b), handempty( )
ontable(a), ontable(b), clear(b),
holding(c), clear(a)
unstack(c,a)
Pre: on(c,a), clear(c), handempty
Del: on(c,a), clear(c), handempty
Add: holding(c), clear(a)
aa b
c
a
c
b
What is the difference
to the formulation
with Negation?

46. CLEAR(A) ONTABLE(A)
CLEAR(B) ONTABLE(B)
CLEAR(C) ONTABLE(C) HANDEMPTY
Search
Space for
Breadth-
First
search
putdown(B) putdown(A)
pickup(B) pickup(A)pickup(C) Putdown(C)
CLEAR(A)
CLEAR(C)
HOLDING(B)
ONTABLE(A)
ONTABLE(C)
CLEAR(A)
CLEAR(B)
HOLDING(C)
ONTABLE(A)
ONTABLE(B)
CLEAR(B)
CLEAR(C)
HOLDING(A)
ONTABLE(B)
ONTABLE(C)
CLEAR(A)
ON(B, C)
CLEAR(B)
ONTABLE(A)
ONTABLE(C)
HANDEMPTY
CLEAR(C)
ON(B, A)
CLEAR(B)
ONTABLE(A)
ONTABLE(C)
HANDEMPTY
CLEAR(A)
ON(C, B)
CLEAR(C)
ONTABLE(A)
ONTABLE(B)
HANDEMPTY
CLEAR(B)
ON(C, A)
CLEAR(C)
ONTABLE(A)
ONTABLE(B)
HANDEMPTY
CLEAR(B)
ON(A, C)
CLEAR(A)
ONTABLE(B)
ONTABLE(C)
HANDEMPTY
c
ba
CLEAR(C)
ON(A, B)
CLEAR(A)
ONTABLE(B)
ONTABLE(C)
HANDEMPTY
ON(B, C)
CLEAR(B)
HOLDING(A)
ONTABLE(C)
ON(B, C)
CLEAR(B)
HOLDING(A)
ONTABLE(C)
ON(B, C)
CLEAR(B)
HOLDING(A)
ONTABLE(C)
ON(B, C)
CLEAR(B)
HOLDING(A)
ONTABLE(C)
ON(B, C)
CLEAR(B)
HOLDING(A)
ONTABLE(C)
ON(B, C)
CLEAR(B)
HOLDING(A)
ONTABLE(C)
pickup(A)
pickup(c)
pickup(A)
pickup(B)
pickup(B)
pickup(C)
putdown(A) putdown(B)
putdown(C) putdown(B)
putdown(B)
putdown(C)
stack(B, C)
stack(B, A)
stack(C, B)
stack(C, A) stack(A, B)
unstack(B, C)
unstack(B, A)
unstack(C, B)
unstack(C, A) unstack(A, B)
stack(A, C) unstack(A, C)
CLEAR(A)
ON(A, B)
ON(B, C)
ONTABLE(C)
HANDEMPTY
CLEAR(C)
ON(C, B)
ON(B, A)
ONTABLE(A)
HANDEMPTY
CLEAR(A)
ON(A, C)
ON(C, B)
ONTABLE(B)
HANDEMPTY
CLEAR(B)
ON(B, C)
ON(C, A)
ONTABLE(A)
HANDEMPTY
CLEAR(B)
ON(B, A)
ON(A, C)
ONTABLE(C)
HANDEMPTY
CLEAR(C)
ON(C, A)
ON(A, B)
ONTABLE(B)
HANDEMPTY
a
b
c
stack(B, C)
stack(B, A)
stack(C, B)
stack(A, C)stack(A, B)
unstack(B, C)
stack(B, A)
unstack(C, B)
unstack(A, C)unstack(A, B)
stack(C, A) unstack(C, A)

47. SHIWANI GUPTA 47
State-Space Search:
State-space planning is a search in the space of states
C
A
B
C
B
A
A
B
C
B
A
C
A
C
B
B
C
A
A B
C
B C
A
A C
B
A B
C
A C
B
B C
A
A B C
Initial
state
Goal

48. SHIWANI GUPTA 48
Practical Planners
• Spacecraft assembly, integration, and verification (eg. OPTIMUM
AIV)
STRIPS cannot express following concepts:
1. Hierarchical plans (since more complicated)
2. Complex conditions (STRIPS operators are propositional)
3. Time (STRIPS assumes that actions occur instantaneously)
4. Resources (limitations to budget, people, things)
• Job Shop Scheduling (eg. O-Plan)
• Scheduling for space missions (eg. PlanERS-1)
• Buildings, aircraft carriers and beer factories (eg. SIPE)

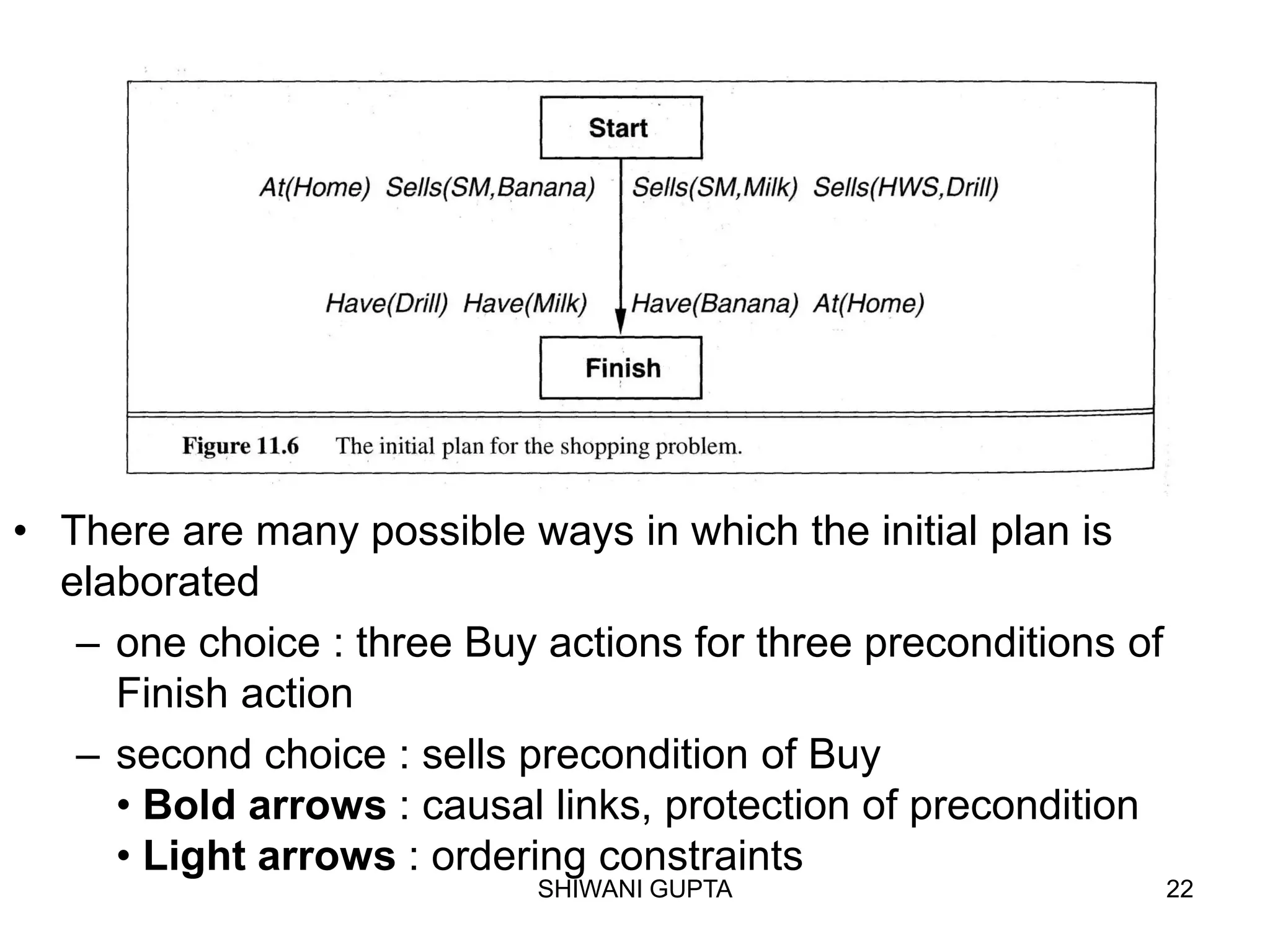
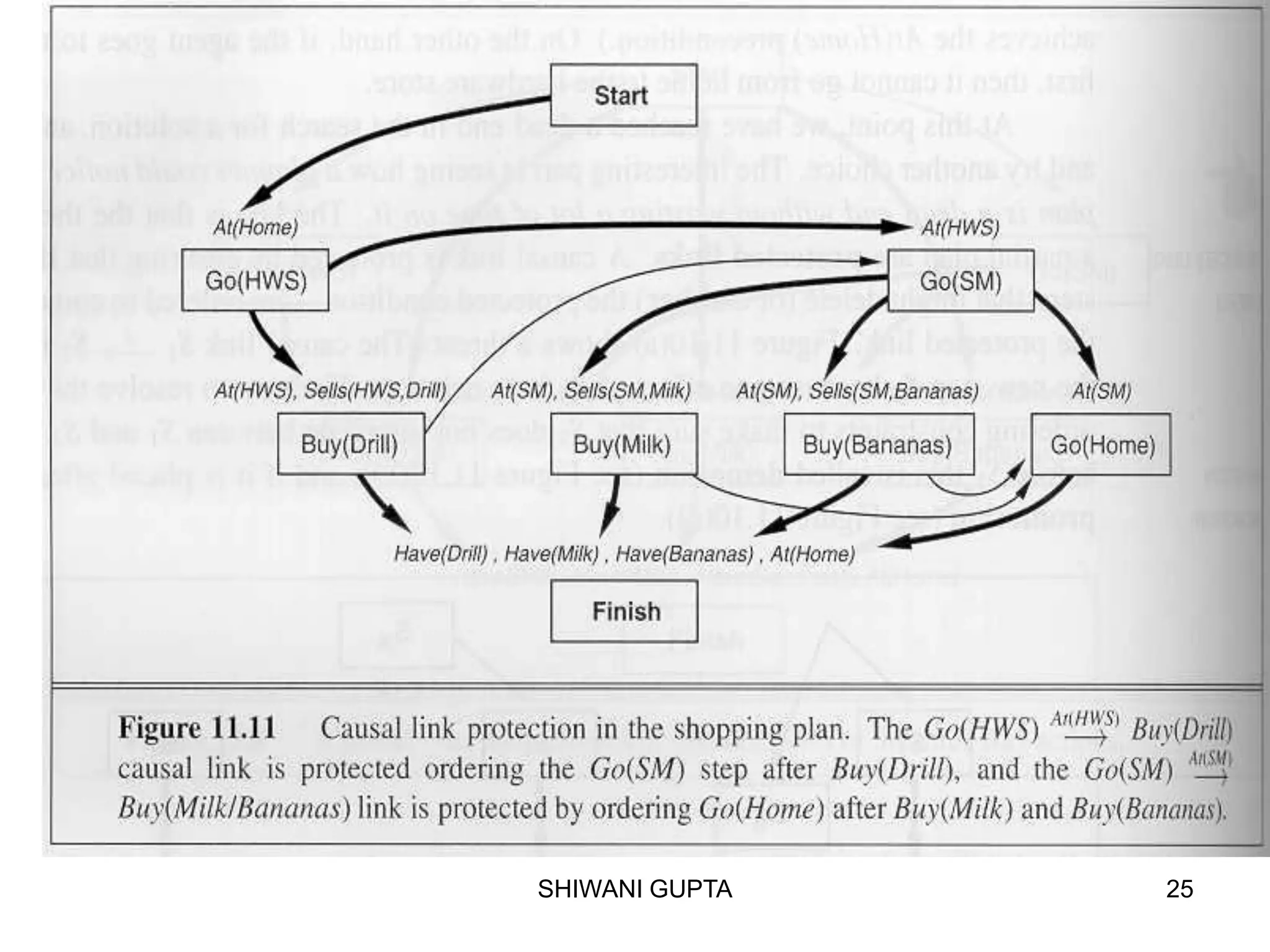
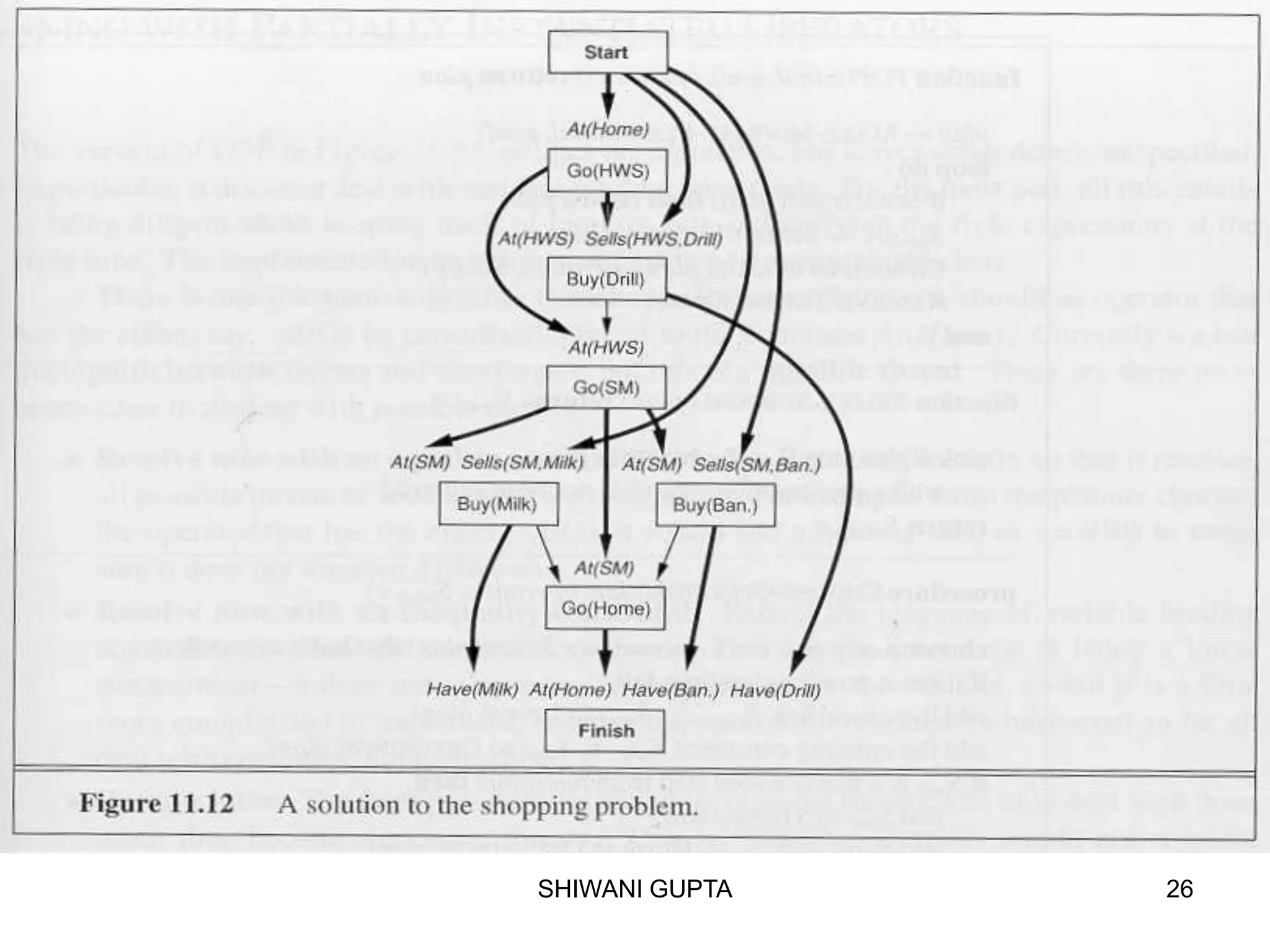
49. SHIWANI GUPTA 49
Hierarchical Decomposition
• Solution at a high level abstraction
[Go(Supermarket),Buy(Milk),Buy(Bananas),Go(Home)]
It is a long way from instruction fed to the agent’s effectors
• A low level plan
[Forward(1 cm),Turn(1 deg),Forward(1 cm), ……]
• Hierarchical decomposition : an abstract operator can
be decomposed into a group of steps
eg. Abstract operator: Build(House)
decomposed operators : obtain Permit,Hire
Builder,Construction, Pay Builder
• Primitive operator:executed by the agent

50. SHIWANI GUPTA 50
Hierarchical planning work

51. SHIWANI GUPTA 51
Extending STRIPS
(1) partition operators into primitive and
nonprimitive operators
nonprimitive : Install(FloorBoards)…..decomposed
into other tasks
primitive : Hammer(Nail)…..directly executable
(2) decomposition method
Decompose(o,p) : An operator o is decomposed into a
plan p

52. SHIWANI GUPTA 52
• Decomposition of o into p
The decomposed plan p correctly implements an
operator if it is complete and consistent :
1. p must be consistent (no contradiction)
2. Every effect of o must be asserted by at least one
step of p
3. Every precondition of the steps in p must be
achieved by a step in p or be one of the
preconditions of o

53. SHIWANI GUPTA 53
Analysis of Hierarchical Decomposition
Abstract solution : a plan containing abstract
operators, but consistent and complete
– downward solution:if p is an abstract solution and
there is a primitive solution
– upward solution:if an abstract plan is inconsistent
then no primitive sol.

54. SHIWANI GUPTA 54
Decomposition and Sharing
• Merge each step of the decomposition into existing plan
• Divide-and-conquer approach:solve each subproblem and then
combine it into the rest
• Sharing steps while merging
• eg. Clear semester exams and get degree
(1) decomposition
• get admission and clear semester exams
• get admission and get degree
(2) merge
• share the step “get admission”

55. SHIWANI GUPTA 55
Decomposition and approximation
• Hierarchical decomposition
nonprimitive operator => primitives
• Hierarchical planning(approximation hierarchy, abstraction
hierarchy)
– It takes an operator and partitions its precondition according
to their criticality level
Op(ACTION:Buy(x),
EFFECT : Have(x)  Have(Money),
PRECOND:1:Sells(store,x) 
2:At(store) 
3:Have(Money))

56. SHIWANI GUPTA 56
Conditional Planning
• Contingency planning : incomplete planning
by constructing a conditional plan that accounts
for each possible situation
• Sensing action:The agent includes sensing
actions to find which part of the plan to be
executed

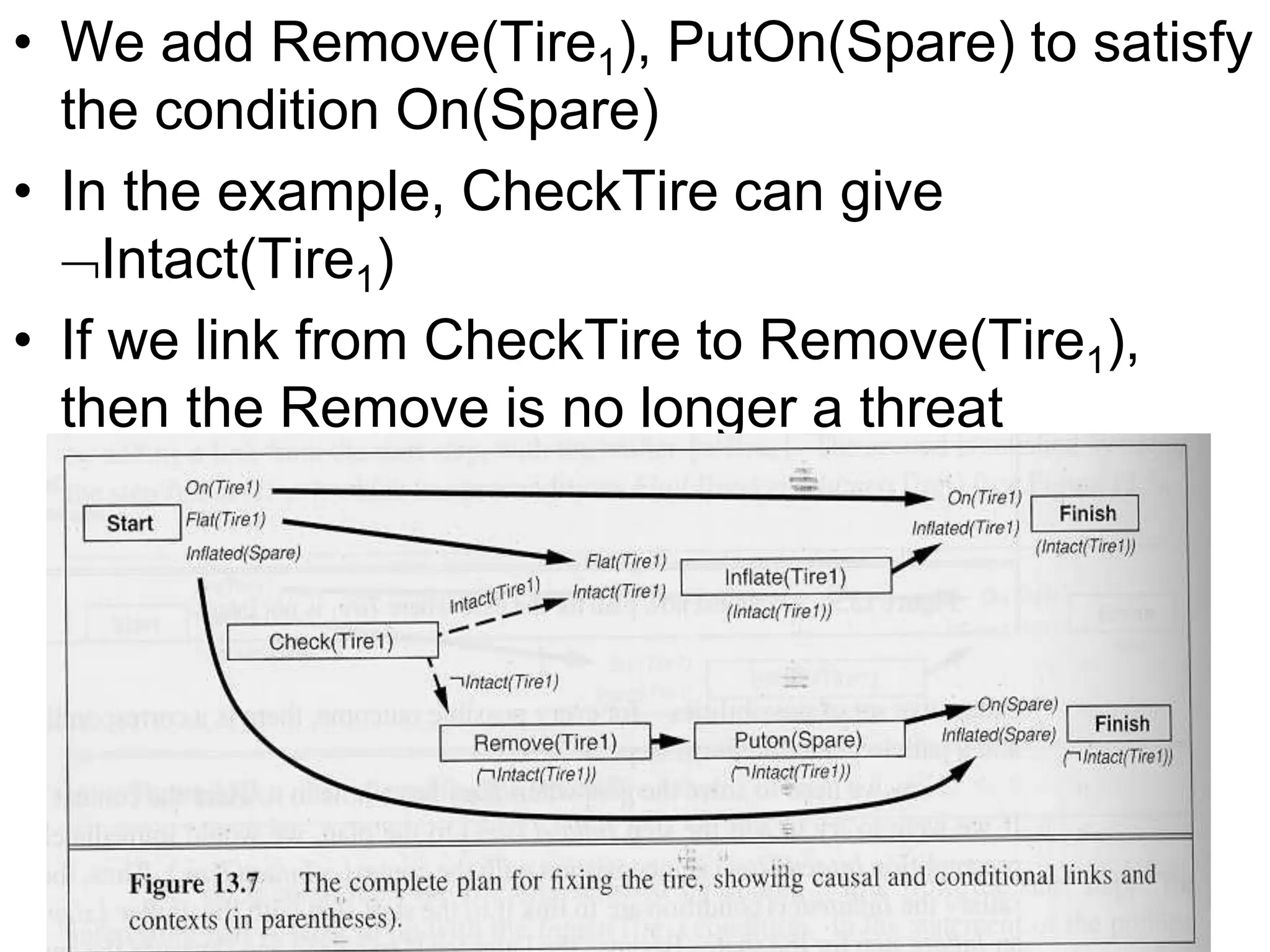
57. SHIWANI GUPTA 57
eg. “Fixing a flat tire”
(1) Possible operators
• Op(ACTION:Remove(x),
PRECOND:On(x),
EFFECT:Off(x)  ClearHub(x)  On(x))
• Op(ACTION:PutOn(x),
PRECOND:Off(x)  ClearHub(x),
EFFECT:On(x)  ClearHub(x)  Off(x))
• Op(ACTION:Inflate(x),
PRECOND:Intact(x)  Flat(x),
EFFECT:Inflated(x)  Flat(x))
(2) goal
• On(x)  Inflated(x)
(3) Initial conditions
• Inflated(Spare)Intact(Spare)Off(Spare)On(Tire1)Flat(Tire1)
(4) Initial plan
• [Remove(Tire1), PutOn(Spare)]

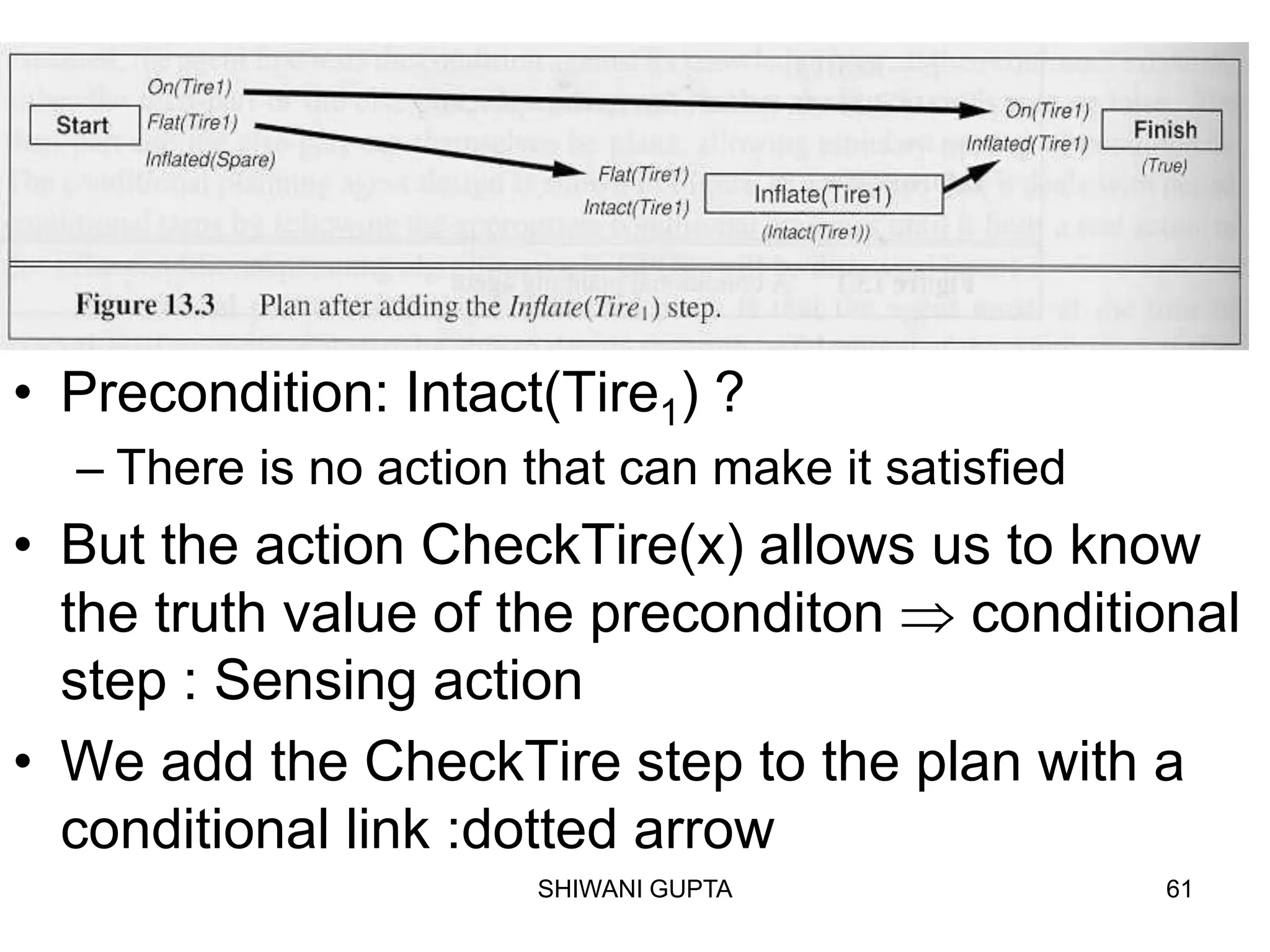
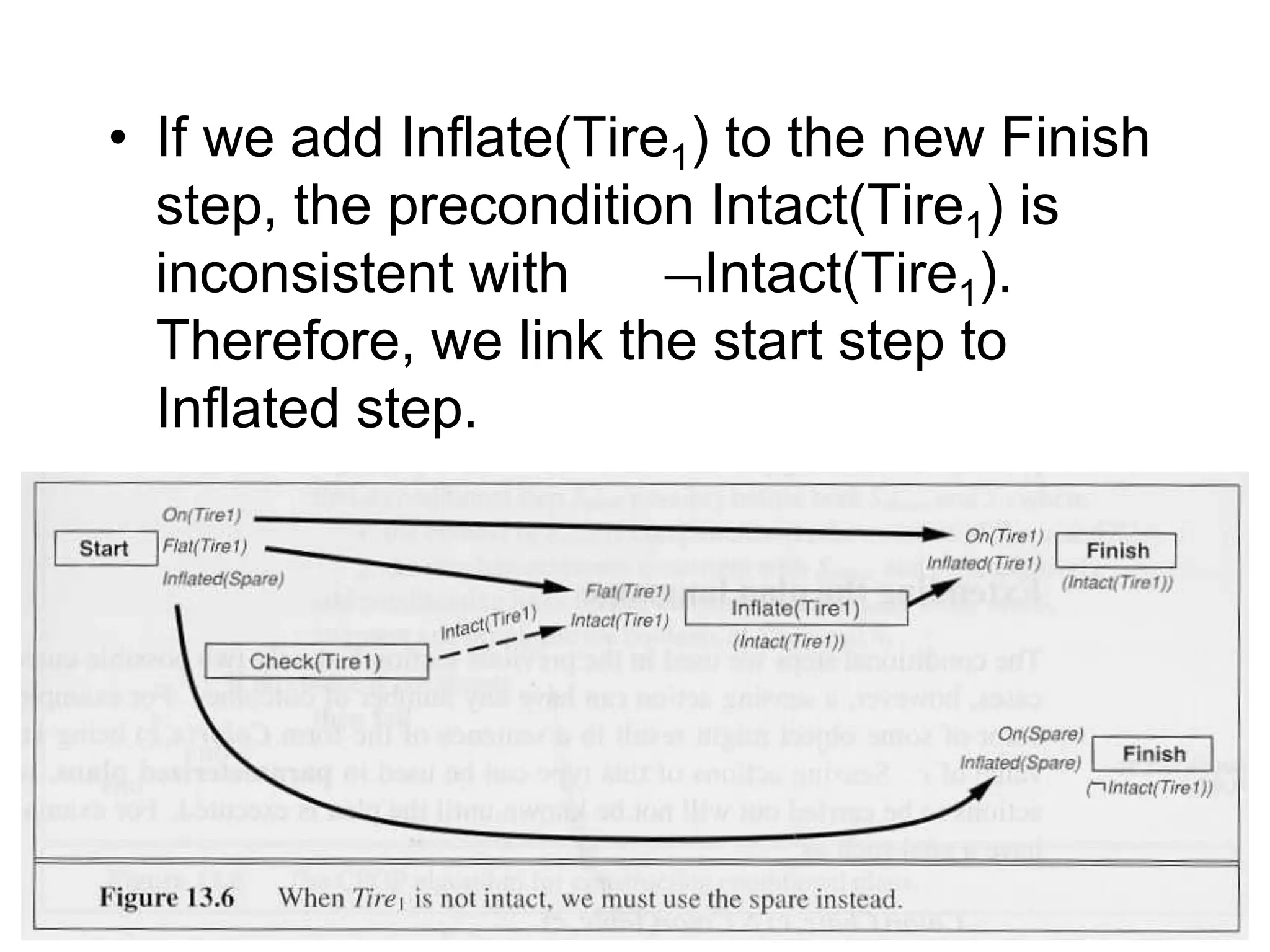
58. SHIWANI GUPTA 58
• The initial plan is good if there is no Intact(Tire1). But, if Tire1 is
intact, only the inflation is needed
• Conditional step
If(<condition>,<ThenPart>,<ElsePart>,)
• If(Intact(Tire1),[Inflate(Tire1)],[Remove(Tire1),
PutOn(Spare)])
• Sensing Action
x,s Tire(x) 
KnowsWhether(“Intact(x)”,Result(CheckTire(x),s))
In our action schema format
• Op(ACTION:CheckTire(x),
PRECOND:Tire(x),
EFFECT:KnowsWhether(“Intact(x)”))

59. SHIWANI GUPTA 59

60. SHIWANI GUPTA 60
• Two open conditions to be resolved
– On(x)
– Inflated(x)
• Introduce operator
– Inflate(Tire1)
– preconditions Flat(Tire1) and Intact(Tire1)

61. SHIWANI GUPTA 61
• Precondition: Intact(Tire1) ?
– There is no action that can make it satisfied
• But the action CheckTire(x) allows us to know
the truth value of the preconditon  conditional
step : Sensing action
• We add the CheckTire step to the plan with a
conditional link :dotted arrow

62. SHIWANI GUPTA 62
• We add steps for the case where Tire1
is not intact: another Finish action

63. SHIWANI GUPTA 63
• If we add Inflate(Tire1) to the new Finish
step, the precondition Intact(Tire1) is
inconsistent with Intact(Tire1).
Therefore, we link the start step to
Inflated step.

64. SHIWANI GUPTA 64
• We add Remove(Tire1), PutOn(Spare) to satisfy
the condition On(Spare)
• In the example, CheckTire can give
Intact(Tire1)
• If we link from CheckTire to Remove(Tire1),
then the Remove is no longer a threat

65. SHIWANI GUPTA 65