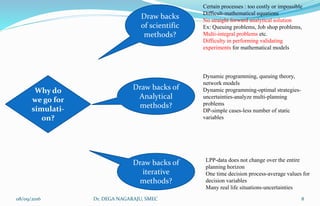
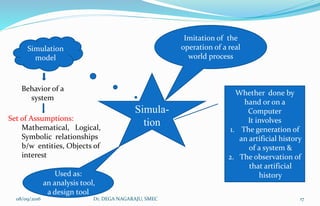
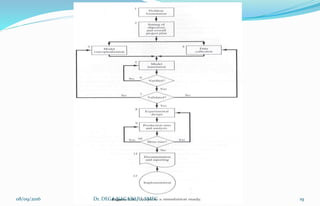
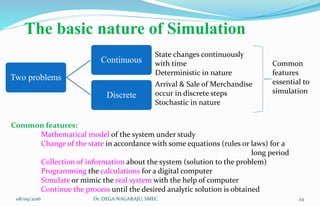
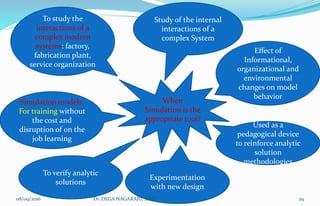
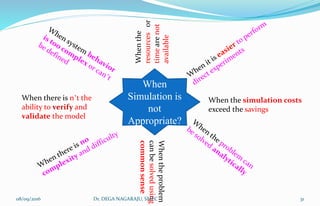
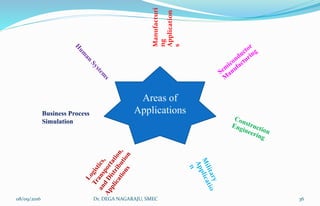
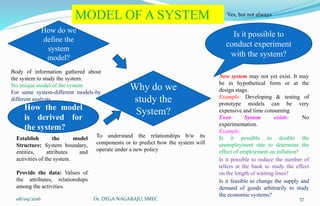
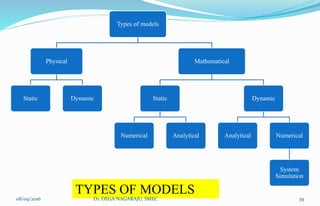
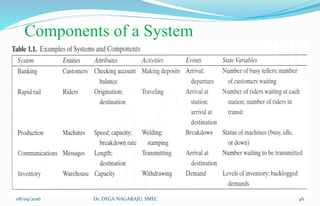
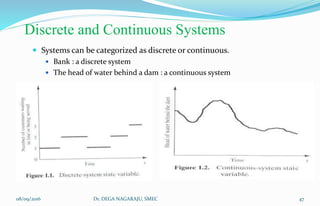
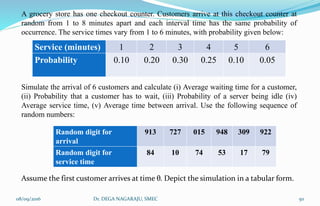
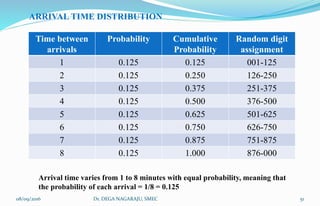
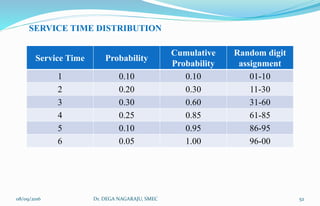
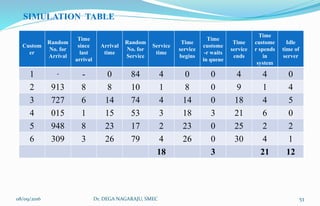
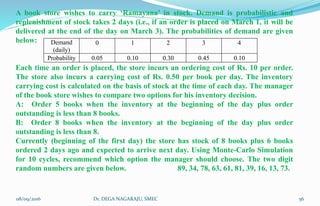
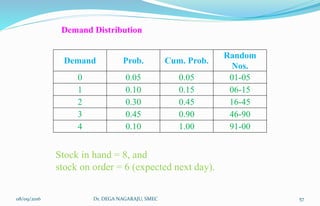
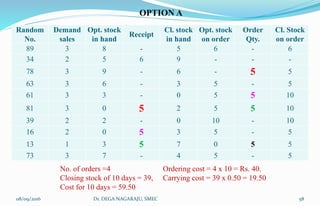
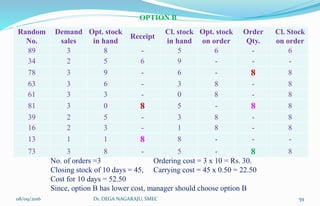
The document outlines the applications, advantages, and disadvantages of simulation as a method for modeling real-world systems and processes across various fields such as manufacturing, business, and government. It discusses the historical development of simulation techniques and emphasizes their utility in understanding complex systems, analyzing performance, and making decisions without disrupting real operations. Additionally, the document highlights circumstances when simulation is appropriate or inappropriate and presents a comprehensive overview of the steps involved in a simulation study.