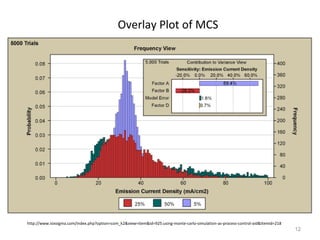
Monte Carlo simulations involve running models multiple times with random inputs to determine probabilities of various outcomes. For each run, random values are selected from ranges for uncertain factors, the model is calculated, and the result recorded. Thousands of runs are typically done to build a pool of results describing the likelihood of different outcomes. The method assumes variables are not influenced by each other. It is useful when probabilities are known but results are hard to determine directly.

1. Monte Carlo Simulations Gary Breaux – Sr. Program manager Oshkosh Defense Nov. 2011

2. In a Monte Carlo simulation, A random value is selected for each of the tasks based on the range of estimates. The model is calculated based on this random value. The result of the model is recorded and the process is repeated.

3. A typical Monte Carlo simulation calculates the model hundreds or thousands of times, each time using different randomly-selected values. The completed simulation yields a large results pool with each result based on random input values. These results are used to describe the likelihood, or probability, of reaching various results in the model.

4. Basic Definition A Monte Carlo Simulation (MCS) yields risk analysis by generating models of possible results through substituting a range of values (a probability distribution)… for any factor that has inherent uncertainty… then running (calculation) cycles… using different sets of random values … from the probability functions… on each cycle.

5. The Monte Carlo method is based on the generation of multiple trials to determine the expected value of a random variable. Vital to the execution is the (mathematical) assumption that each (project) variable/activity being simulated is NOT influenced by other variables (tasks).

6. Schema of the Monte Carlo Method; Generate random values (formulas) for each of the activities (cost/time). =RAND()*(20,000-10,000)+10,000 (generates a random value between 10,000 and 20,000) Sum each series of random values to arrive at the total project (cost/time).

7. Three Point Estimates Three point estimates are the weighted average of three estimates for a particular task based on predictive distribution of possible outcomes against a set of choices as; B est-Case ( conservative ) M ost-Likely ( expected ) W orst-Case ( extreme )

8. Three Point Estimates cont. The formula is expressed as (E=Estimate): E = (B + 4 M + W)/6 B = Best-Case (x1) M = Most-Likely (x4) W = Worst-Case (x1) Best-Case estimate + 4X the Most Likely estimate + the Worst Case estimate / 6 = Estimate (E).

9. Caveats Depending on; the number of uncertainties and the ranges specified for them A MCS could calculate 1k/10k cycles to complete (“skewness”). The technique works particularly well when; the underlying probabilities are known but the results are difficult to determine.

10. Essential Construct a.k.a. the “ Three Point Estimate ” (“ TIME ” on EACH project task/activity ) Best-Case (Min.) Most-Likely (Mean) Worst-Case (Max.) The 3-point estimate approach does not mathematically consider Complexity.

11. Execute the Monte Carlo Method (Time) Generate/utilize random (time) values for each activity (RAND function) from relevant sets of data i.e. specific project time elements. Determine the number of iterations to run the simulation. Apply the values. Run the MCS. Apply (graphically) the distribution/analysis.

12. Overlay Plot of MCS http://www.isixsigma.com/index.php?option=com_k2&view=item&id=925:using-monte-carlo-simulation-as-process-control-aid&Itemid=218

13. MCS (a MATLAB plot)

14. Tools/Reference Primavera Risk Analysis (Risk Analysis - Primavera). @RISK (Risk Analysis and M.C.S. - Palisade). ARM (Active Risk Manager – Deltek). Crystal Ball (Predictive Modeling - Oracle). MATLAB (Mathworks - computational analysis - data interpolation/presentation). http://physics.gac.edu/~huber/envision/instruct/montecar.htm