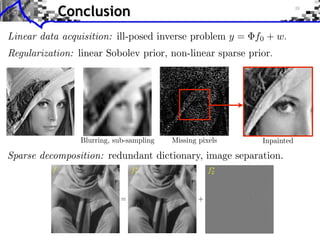
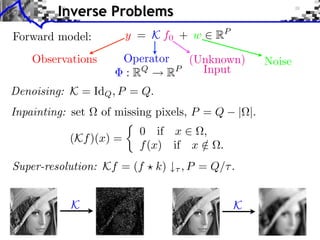
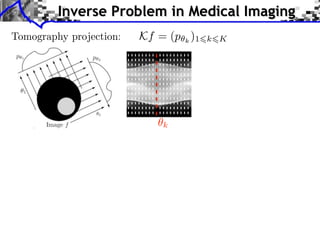
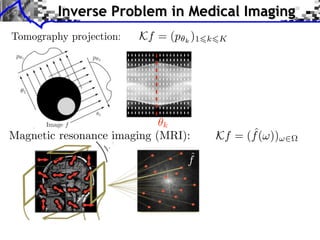
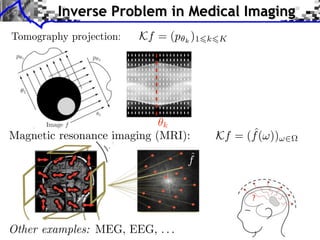
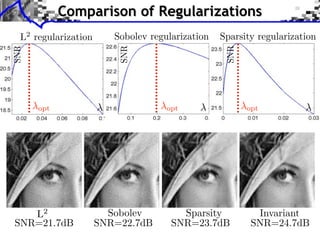
The document discusses sparse regularization for inverse problems. It describes how sparse regularization can be used for tasks like denoising, inpainting, and image separation by posing them as optimization problems that minimize data fidelity and an L1 sparsity prior on the coefficients. Iterative soft thresholding is presented as an algorithm for solving the noisy sparse regularization problem. Examples are given of how sparse wavelet regularization can outperform other regularizers like Sobolev for tasks like image deblurring.

1. Sparse Regularization
Of Inverse Problems
Gabriel Peyré
www.numerical-tours.com

2. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Examples: Sparse Wavelet Regularizations
• Iterative Soft Thresholding
• Sparse Seismic Deconvolution

3. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input

4. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.

5. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.
Inpainting: set of missing pixels, P = Q | |.
0 if x ,
(Kf )(x) =
f (x) if x / .
K

6. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.
Inpainting: set of missing pixels, P = Q | |.
0 if x ,
(Kf )(x) =
f (x) if x / .
Super-resolution: Kf = (f k) , P = Q/ .
K K

7. Inverse Problem in Medical Imaging
Kf = (p k )1 k K

8. Inverse Problem in Medical Imaging
Kf = (p k )1 k K
Magnetic resonance imaging (MRI): ˆ
Kf = (f ( ))
ˆ
f

9. Inverse Problem in Medical Imaging
Kf = (p k )1 k K
Magnetic resonance imaging (MRI): ˆ
Kf = (f ( ))
ˆ
f
Other examples: MEG, EEG, . . .

10. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.

11. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity

12. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity
Choice of : tradeo
Noise level Regularity of f0
||w|| J(f0 )

13. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity
Choice of : tradeo
Noise level Regularity of f0
||w|| J(f0 )
No noise: 0+ , minimize f argmin J(f )
f RQ ,Kf =y

14. Smooth and Cartoon Priors
J(f ) = || f (x)||2 dx
| f |2

15. Smooth and Cartoon Priors
J(f ) = || f (x)||2 dx
J(f ) = || f (x)||dx
J(f ) = length(Ct )dt
R
| f |2 | f|

16. Inpainting Example
Input y = Kf0 + w Sobolev Total variation

17. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Examples: Sparse Wavelet Regularizations
• Iterative Soft Thresholding
• Sparse Seismic Deconvolution

18. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
Q
N

19. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
Fourier: m = ei ·, m
frequency
Q
N

20. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
m = (j, , n)
Fourier: m =e i ·, m
frequency scale position
Wavelets:
m = (2 j
R x n) orientation
=1 =2
Q
N

21. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
m = (j, , n)
Fourier: m =e i ·, m
frequency scale position
Wavelets:
m = (2 j
R x n) orientation
DCT, Curvelets, bandlets, . . .
=1 =2
Q
N

22. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
m = (j, , n)
Fourier: m =e i ·, m
frequency scale position
Wavelets:
m = (2 j
R x n) orientation
DCT, Curvelets, bandlets, . . .
Synthesis: f = m xm m = x. =1 =2
Q =f
x
N
Coe cients x Image f = x

23. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Image f0

24. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Sparse approximation: f = x where
argmin ||f0 x||2 + T 2 J0 (x)
x2RN
Image f0

25. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Sparse approximation: f = x where
argmin ||f0 x||2 + T 2 J0 (x)
x2RN
Orthogonal : = = IdN
f0 , m if | f0 , m | > T,
xm =
0 otherwise. ST Image f0
f= ST (f0 )

26. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Sparse approximation: f = x where
argmin ||f0 x||2 + T 2 J0 (x)
x2RN
Orthogonal : = = IdN
f0 , m if | f0 , m | > T,
xm =
0 otherwise. ST Image f0
f= ST (f0 )
Non-orthogonal :
NP-hard.

27. Convex Relaxation: L1 Prior
J0 (x) = # {m xm = 0}
J0 (x) = 0 null image.
Image with 2 pixels: J0 (x) = 1 sparse image.
J0 (x) = 2 non-sparse image.
x2
x1
q=0

28. Convex Relaxation: L1 Prior
J0 (x) = # {m xm = 0}
J0 (x) = 0 null image.
Image with 2 pixels: J0 (x) = 1 sparse image.
J0 (x) = 2 non-sparse image.
x2
x1
q=0 q = 1/2 q=1 q = 3/2 q=2
q
priors: Jq (x) = |xm |q (convex for q 1)
m

29. Convex Relaxation: L1 Prior
J0 (x) = # {m xm = 0}
J0 (x) = 0 null image.
Image with 2 pixels: J0 (x) = 1 sparse image.
J0 (x) = 2 non-sparse image.
x2
x1
q=0 q = 1/2 q=1 q = 3/2 q=2
q
priors: Jq (x) = |xm |q (convex for q 1)
m
Sparse 1
prior: J1 (x) = |xm |
m

30. L1 Regularization
x0 RN
coe cients

31. L1 Regularization
x0 RN f0 = x0 RQ
coe cients image

32. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w

33. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w
= K ⇥ ⇥ RP N

34. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w
= K ⇥ ⇥ RP N
Sparse recovery: f = x where x solves
1
min ||y x||2 + ||x||1
x RN 2
Fidelity Regularization

35. Noiseless Sparse Regularization
Noiseless measurements: y = x0
x
x=
y
x argmin |xm |
x=y m

36. Noiseless Sparse Regularization
Noiseless measurements: y = x0
x
x
x= x=
y y
x argmin |xm | x argmin |xm |2
x=y m x=y m

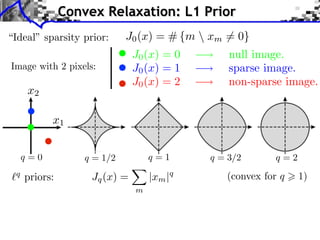
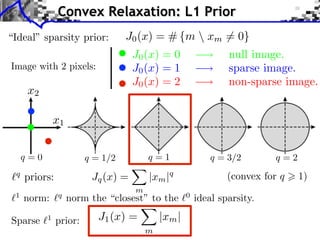
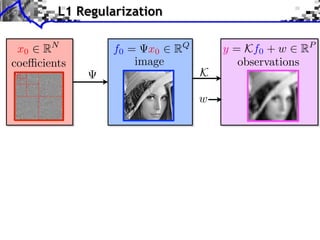
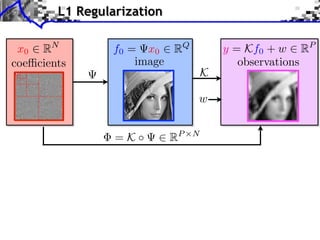
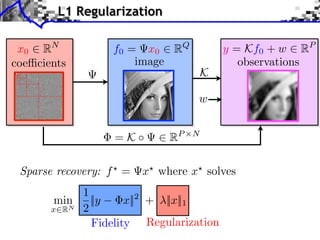
37. Noiseless Sparse Regularization
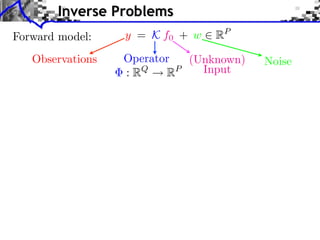
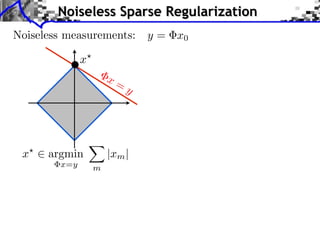
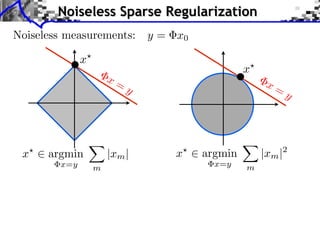
Noiseless measurements: y = x0
x
x
x= x=
y y
x argmin |xm | x argmin |xm |2
x=y m x=y m
Convex linear program.
Interior points, cf. [Chen, Donoho, Saunders] “basis pursuit”.
Douglas-Rachford splitting, see [Combettes, Pesquet].

38. Noisy Sparse Regularization
Noisy measurements: y = x0 + w
1
x argmin ||y x||2 + ||x||1
x RQ 2
Data fidelity Regularization

39. Noisy Sparse Regularization
Noisy measurements: y = x0 + w
1
x argmin ||y x||2 + ||x||1
x RQ 2 Equivalence
Data fidelity Regularization
x argmin ||x||1
|| x y||
|
x=
x y|

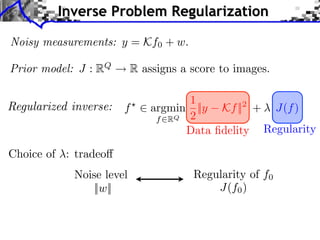
40. Noisy Sparse Regularization
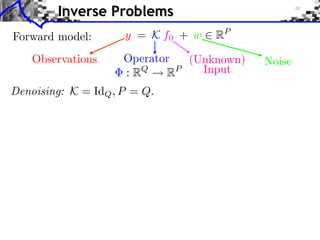
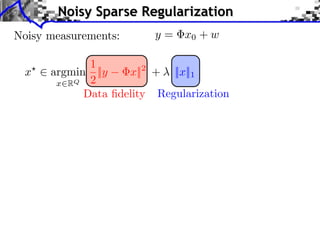
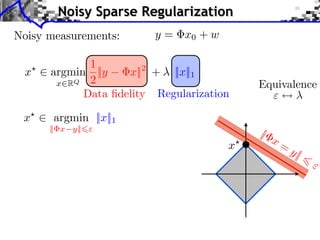
Noisy measurements: y = x0 + w
1
x argmin ||y x||2 + ||x||1
x RQ 2 Equivalence
Data fidelity Regularization
x argmin ||x||1
|| x y||
|
x=
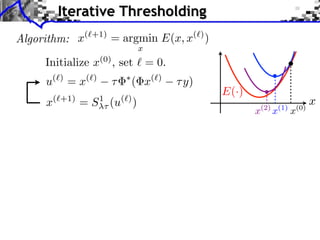
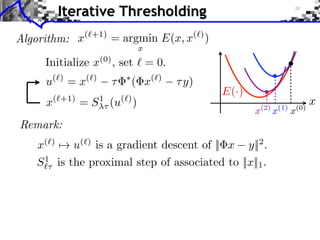
Algorithms: x y|
Iterative soft thresholding
Forward-backward splitting
see [Daubechies et al], [Pesquet et al], etc
Nesterov multi-steps schemes.

41. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Examples: Sparse Wavelet Regularizations
• Iterative Soft Thresholding
• Sparse Seismic Deconvolution

42. Image De-blurring
Original f0 y = h f0 + w

43. Image De-blurring
Original f0 y = h f0 + w Sobolev
SNR=22.7dB
Sobolev regularization: f = argmin ||f ⇥ h y||2 + ||⇥f ||2
f RN
ˆ
h(⇥)
ˆ
f (⇥) = y (⇥)
ˆ
ˆ
|h(⇥)|2 + |⇥|2

44. Image De-blurring
Original f0 y = h f0 + w Sobolev Sparsity
SNR=22.7dB SNR=24.7dB
Sobolev regularization: f = argmin ||f ⇥ h y||2 + ||⇥f ||2
f RN
ˆ
h(⇥)
ˆ
f (⇥) = y (⇥)
ˆ
ˆ
|h(⇥)|2 + |⇥|2
Sparsity regularization: = translation invariant wavelets.
1
f = x where x argmin ||h ( x) y||2 + ||x||1
x 2

45. Comparison of Regularizations
L2 regularization Sobolev regularization Sparsity regularization
SNR
SNR
SNR
opt opt opt
L2 Sobolev Sparsity Invariant
SNR=21.7dB SNR=22.7dB SNR=23.7dB SNR=24.7dB

46. Inpainting Problem
K 0 if x ,
(Kf )(x) =
f (x) if x / .
Measures: y = Kf0 + w

47. Image Separation
Model: f = f1 + f2 + w, (f1 , f2 ) components, w noise.

48. Image Separation
Model: f = f1 + f2 + w, (f1 , f2 ) components, w noise.

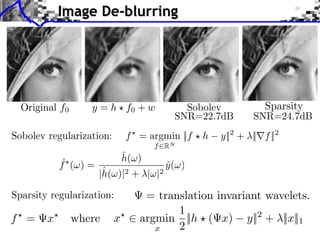
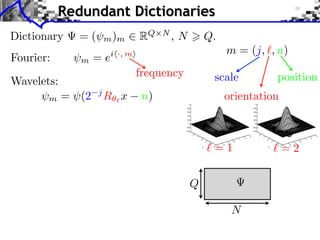
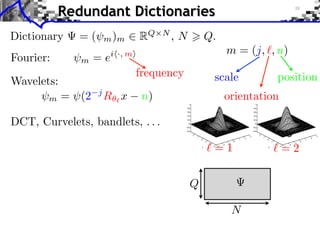
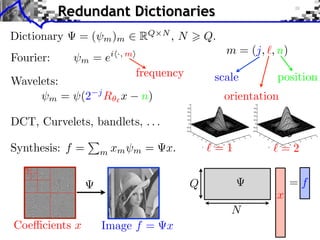
49. Image Separation
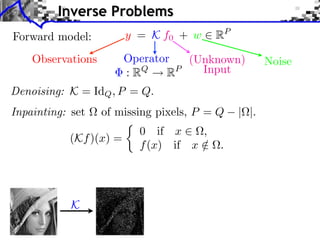
Model: f = f1 + f2 + w, (f1 , f2 ) components, w noise.
Union dictionary: =[ 1, 2] RQ (N1 +N2 )
Recovered component: fi = i xi .
1
(x1 , x2 ) argmin ||f x||2 + ||x||1
x=(x1 ,x2 ) RN 2

50. Examples of Decompositions

51. Cartoon+Texture Separation

52. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Examples: Sparse Wavelet Regularizations
• Iterative Soft Thresholding
• Sparse Seismic Deconvolution

53. Sparse Regularization Denoising
Denoising: y = x0 + w 2 RN , K = Id.
⇤ ⇤
Orthogonal-basis: = IdN , x = f.
Regularization-based denoising:
1
x = argmin ||x y||2 + J(x)
?
x2RN 2
P
Sparse regularization: J(x) = m |xm |q
(where |a|0 = (a))

54. Sparse Regularization Denoising
Denoising: y = x0 + w 2 RN , K = Id.
⇤ ⇤
Orthogonal-basis: = IdN , x = f.
Regularization-based denoising:
1
x = argmin ||x y||2 + J(x)
?
x2RN 2
P
Sparse regularization: J(x) = m |xm |q
(where |a|0 = (a))
q
x?
m = ST (xm )

55. Surrogate Functionals
Sparse regularization:
? 1
x 2 argmin E(x) = ||y x||2 + ||x||1
x2RN 2
⇤
Surrogate functional: ⌧ < 1/|| ||
1 2 1
E(x, x) = E(x)
˜ || (x x)|| + ||x
˜ x||2
˜
2 2⌧
E(·, x)
˜
E(·)
x
S ⌧ (u) x
˜

56. Surrogate Functionals
Sparse regularization:
? 1
x 2 argmin E(x) = ||y x||2 + ||x||1
x2RN 2
⇤
Surrogate functional: ⌧ < 1/|| ||
1 2 1
E(x, x) = E(x)
˜ || (x x)|| + ||x
˜ x||2
˜
2 2⌧
E(·, x)
˜
Theorem:
argmin E(x, x) = S ⌧ (u)
˜ E(·)
x
⇤
where u = x ⌧ ( x x)
˜
x
S ⌧ (u) x
˜
Proof: E(x, x) / 1 ||u
˜ 2 x||2 + ||x||1 + cst.

57. Iterative Thresholding
Algorithm: x(`+1) = argmin E(x, x(`) )
x
Initialize x(0) , set ` = 0.
⇤
u(`) = x(`) ⌧ ( x(`) ⌧ y)
E(·)
x(`+1) = S 1⌧ (u(`) ) (2) (1) (0)
x
x x x

58. Iterative Thresholding
Algorithm: x(`+1) = argmin E(x, x(`) )
x
Initialize x(0) , set ` = 0.
⇤
u(`) = x(`) ⌧ ( x(`) ⌧ y)
E(·)
x(`+1) = S 1⌧ (u(`) ) (2) (1) (0)
x
x x x
Remark:
x(`) 7! u(`) is a gradient descent of || x y||2 .
1
S`⌧ is the proximal step of associated to ||x||1 .

59. Iterative Thresholding
Algorithm: x(`+1) = argmin E(x, x(`) )
x
Initialize x(0) , set ` = 0.
⇤
u(`) = x(`) ⌧ ( x(`) ⌧ y)
E(·)
x(`+1) = S 1⌧ (u(`) ) (2) (1) (0)
x
x x x
Remark:
x(`) 7! u(`) is a gradient descent of || x y||2 .
1
S`⌧ is the proximal step of associated to ||x||1 .
⇤
Theorem: if ⌧ < 2/|| ||, then x(`) ! x? .

60. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Examples: Sparse Wavelet Regularizations
• Iterative Soft Thresholding
• Sparse Seismic Deconvolution

61. Seismic Imaging

62. 1D Idealization
Initial condition: “wavelet”
= band pass filter h
1D propagation convolution
f =h f
h(x)
f
ˆ
h( )
y = f0 h + w P

63. Pseudo Inverse
Pseudo-inverse:
ˆ+ ( ) = y ( )
f
ˆ
= f + = h+ ⇥ y = f0 + h+ ⇥ w
h( )
ˆ ˆ
where h+ ( ) = h( ) 1
ˆ ˆ
Stabilization: h+ (⇥) = 0 if |h(⇥)|
ˆ
h( ) y = h f0 + w
ˆ
1/h( )
f+

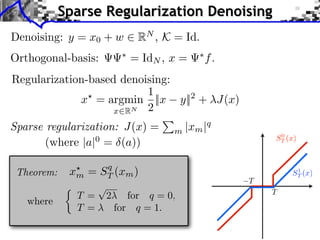
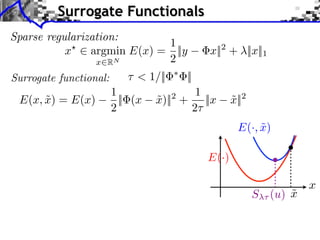
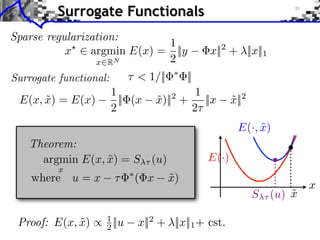
64. Sparse Spikes Deconvolution
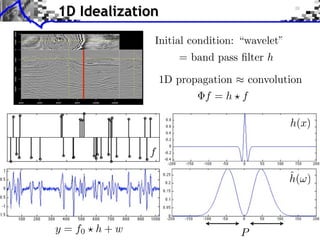
f with small ||f ||0 y=f h+w
Sparsity basis: Diracs ⇥m [x] = [x m]
1
f = argmin ||f ⇥ h y||2 + |f [m]|.
f RN 2 m

65. Sparse Spikes Deconvolution
f with small ||f ||0 y=f h+w
Sparsity basis: Diracs ⇥m [x] = [x m]
1
f = argmin ||f ⇥ h y||2 + |f [m]|.
f RN 2 m
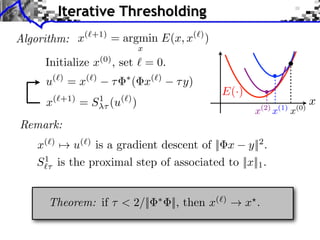
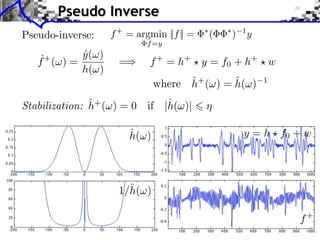
Algorithm: < 2/|| ˆ
|| = 2/max |h(⇥)|2
˜
• Inversion: f (k) = f (k) h ⇥ (h ⇥ f (k) y).
˜
f (k+1) [m] = S 1⇥ (f (k) [m])

66. Numerical Example
f0
Choosing optimal :
oracle, minimize ||f0 f ||
y=f h+w
SNR(f0 , f )
f

67. Convergence Study
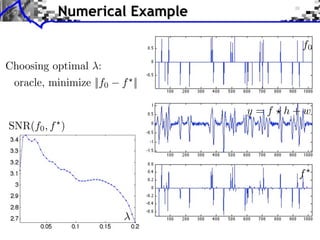
Sparse deconvolution:f = argmin E(f ).
f RN
1
Energy: E(f ) = ||h ⇥ f y||2 + |f [m]|.
2 m
Not strictly convex = no convergence speed.
log10 (E(f (k) )/E(f ) 1) log10 (||f (k) f ||/||f0 ||)
k k

68. Conclusion

69. Conclusion

70. Conclusion