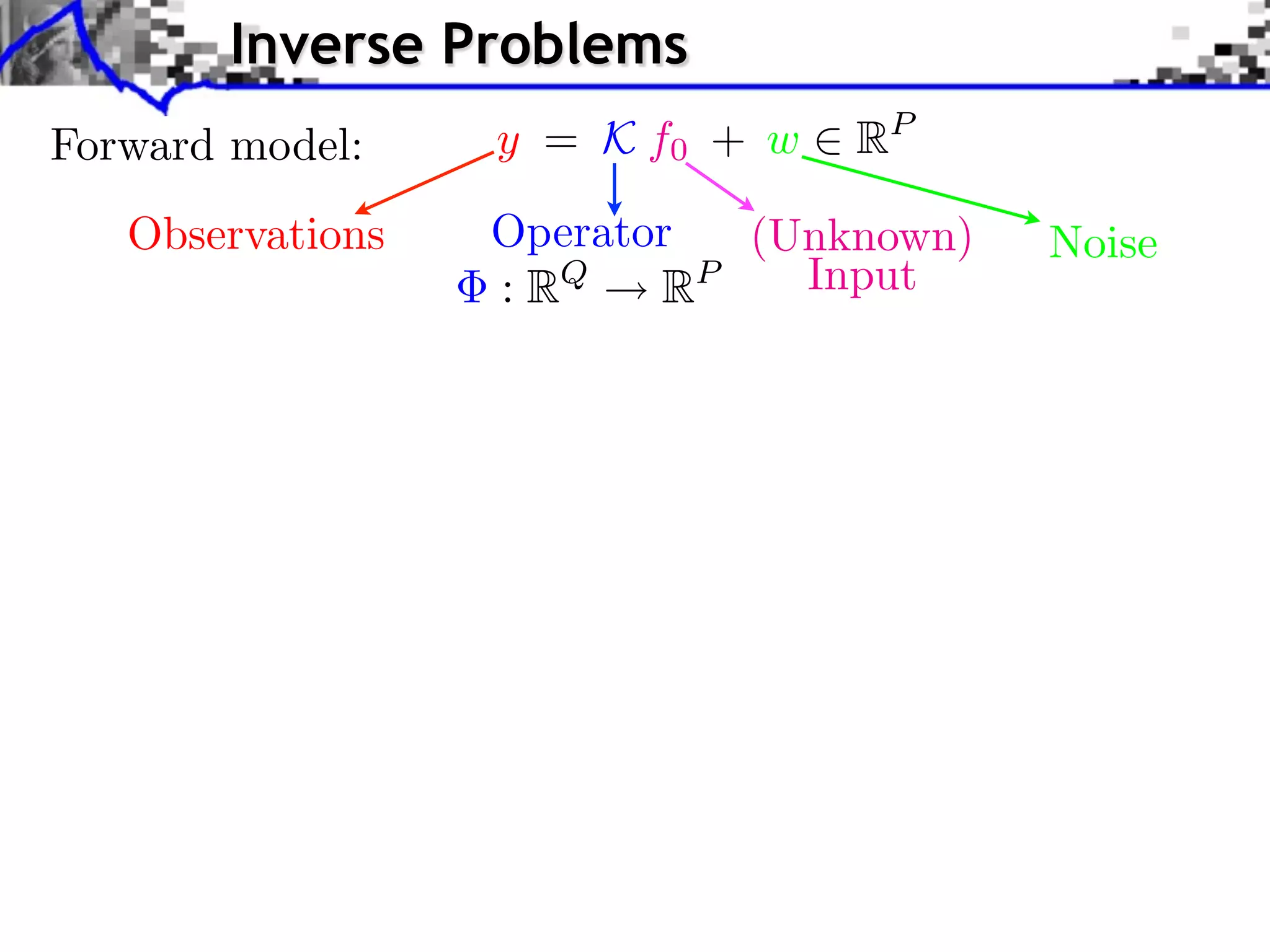
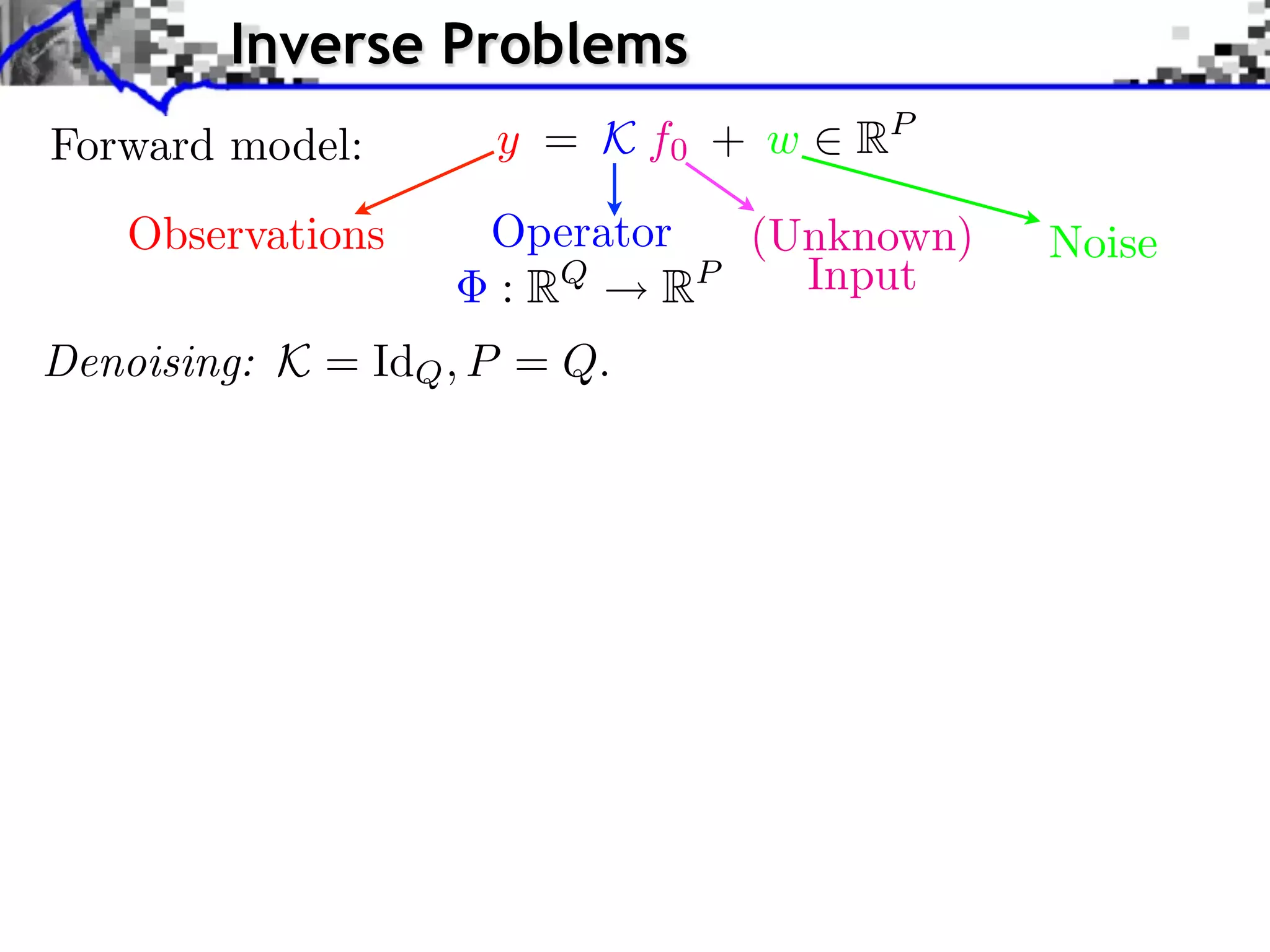
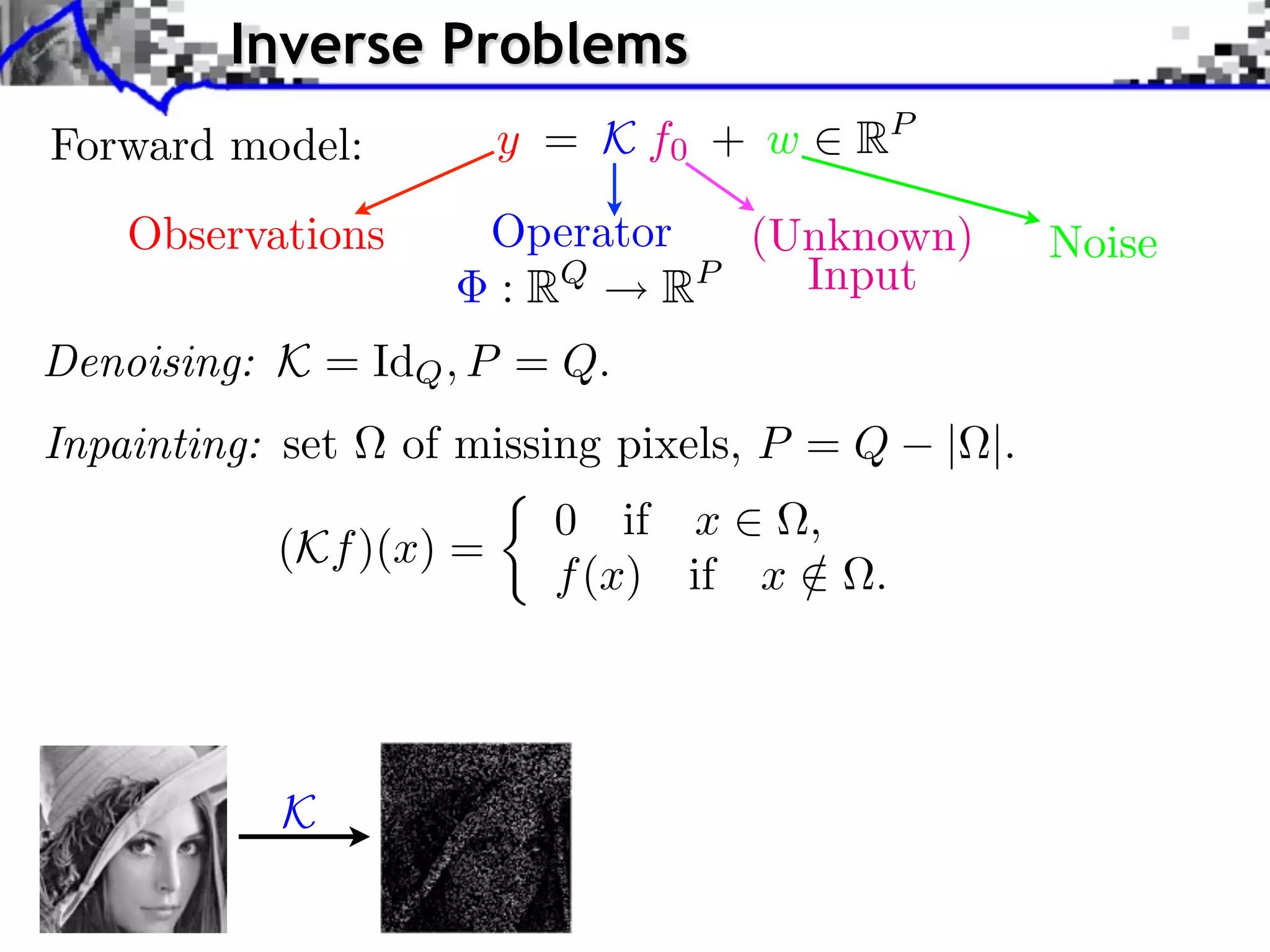
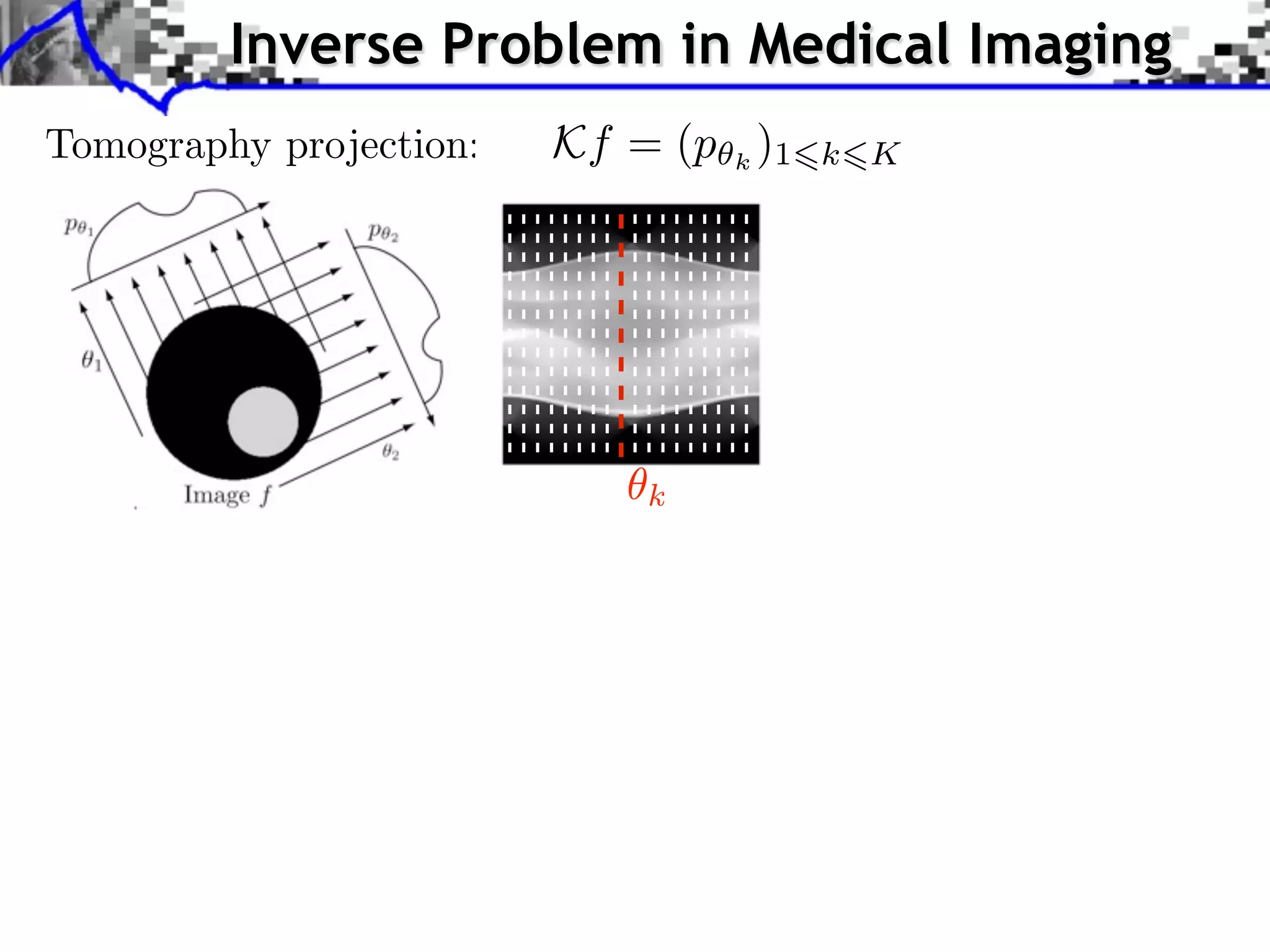
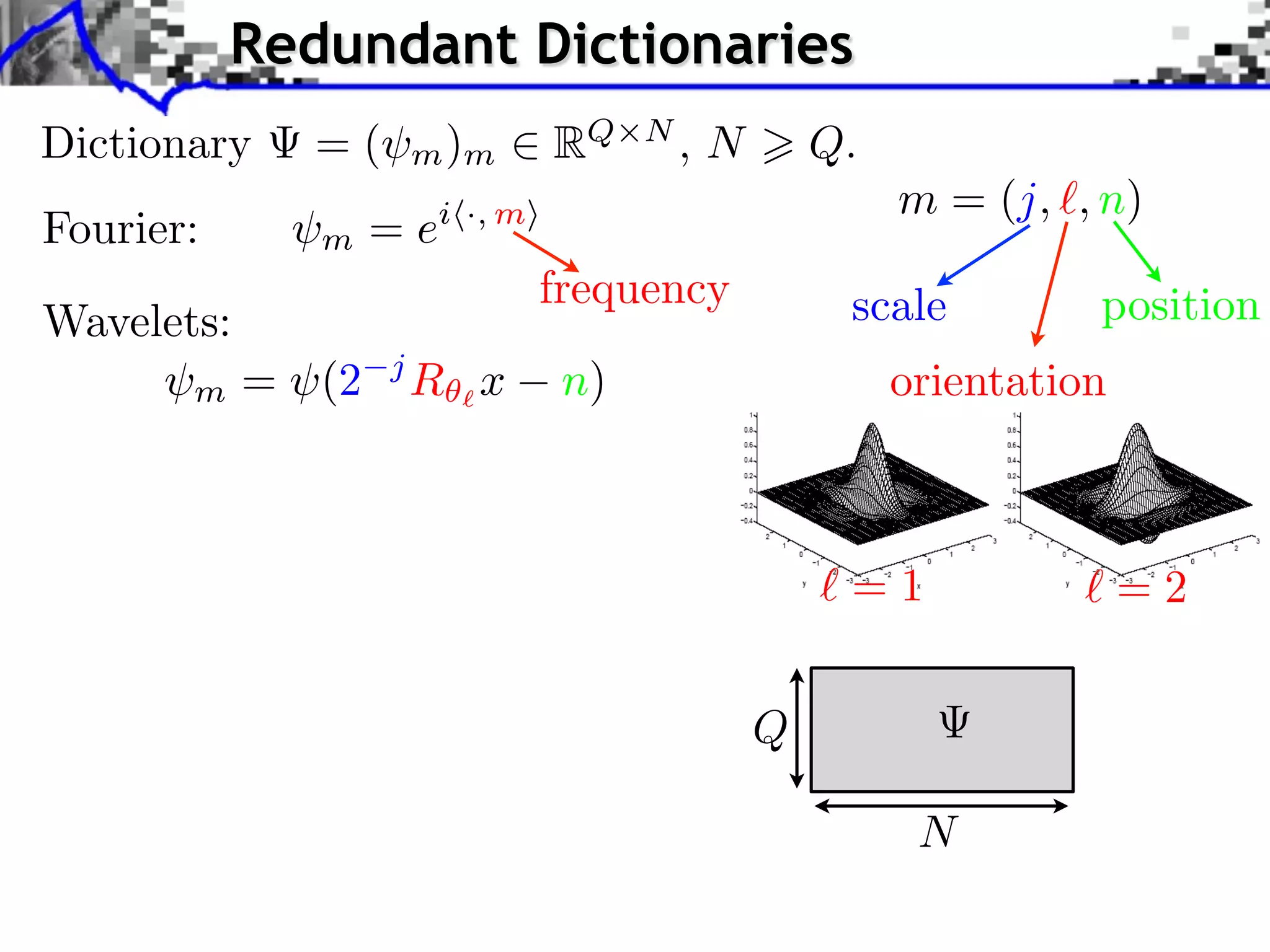
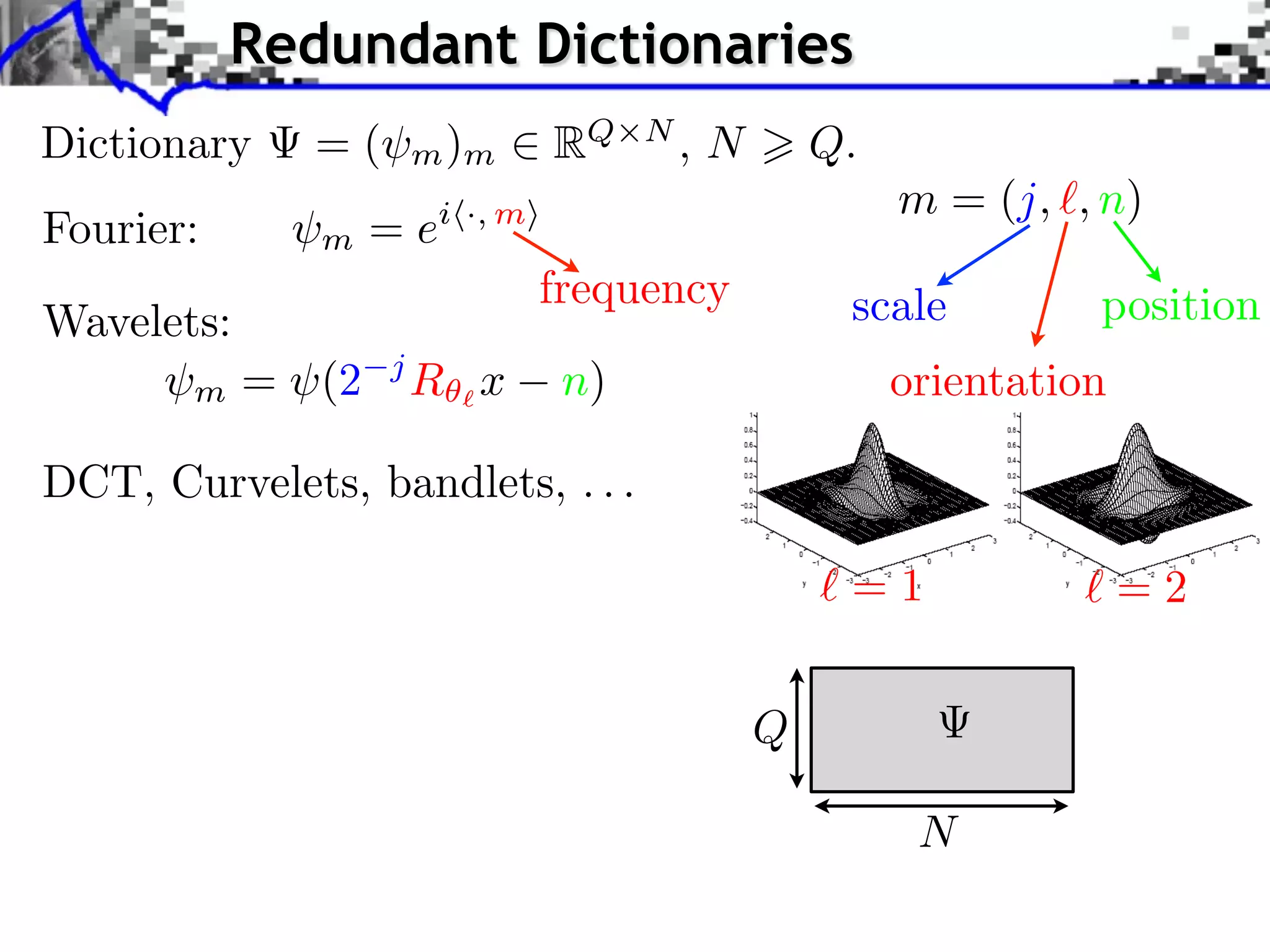
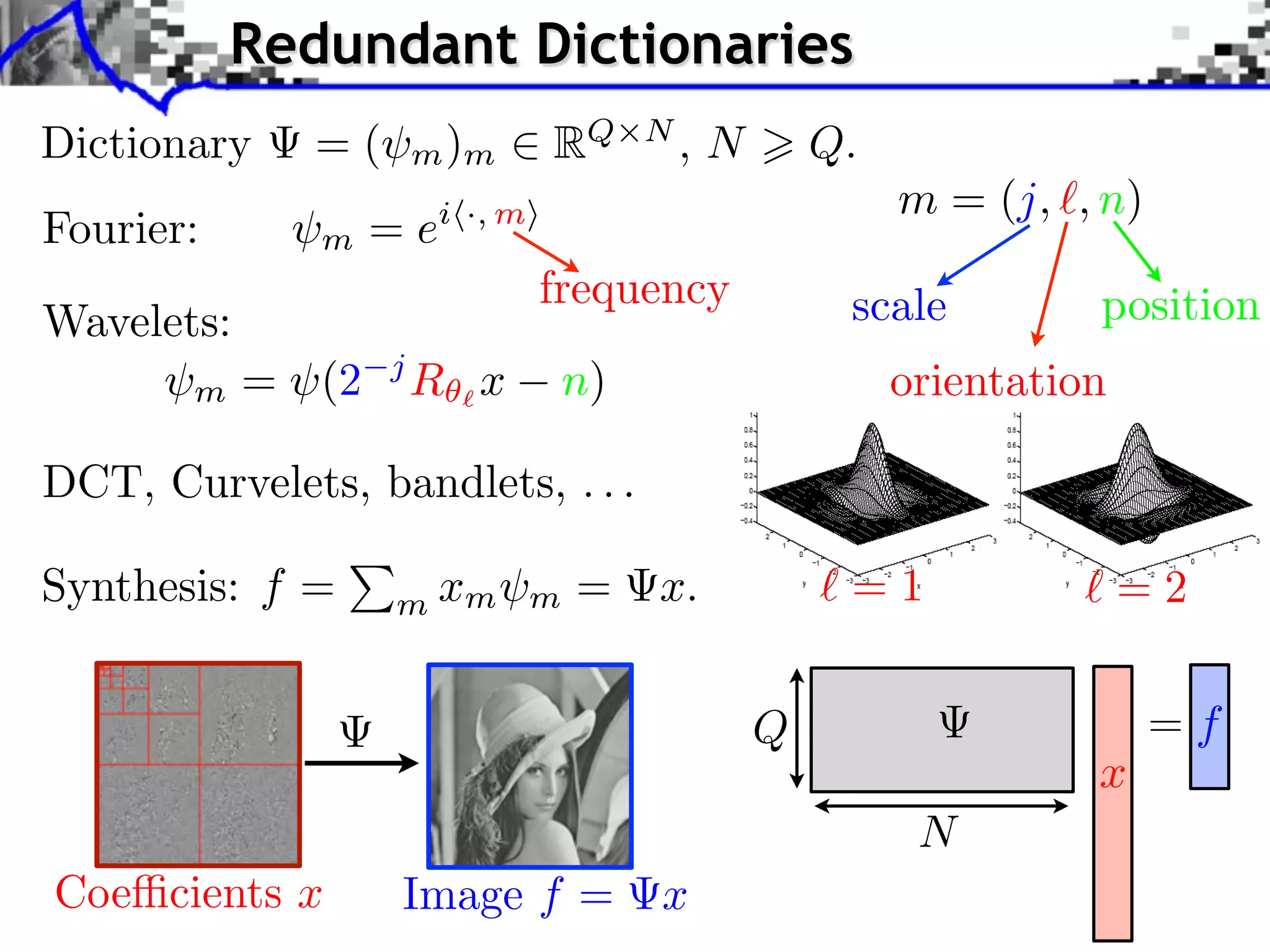
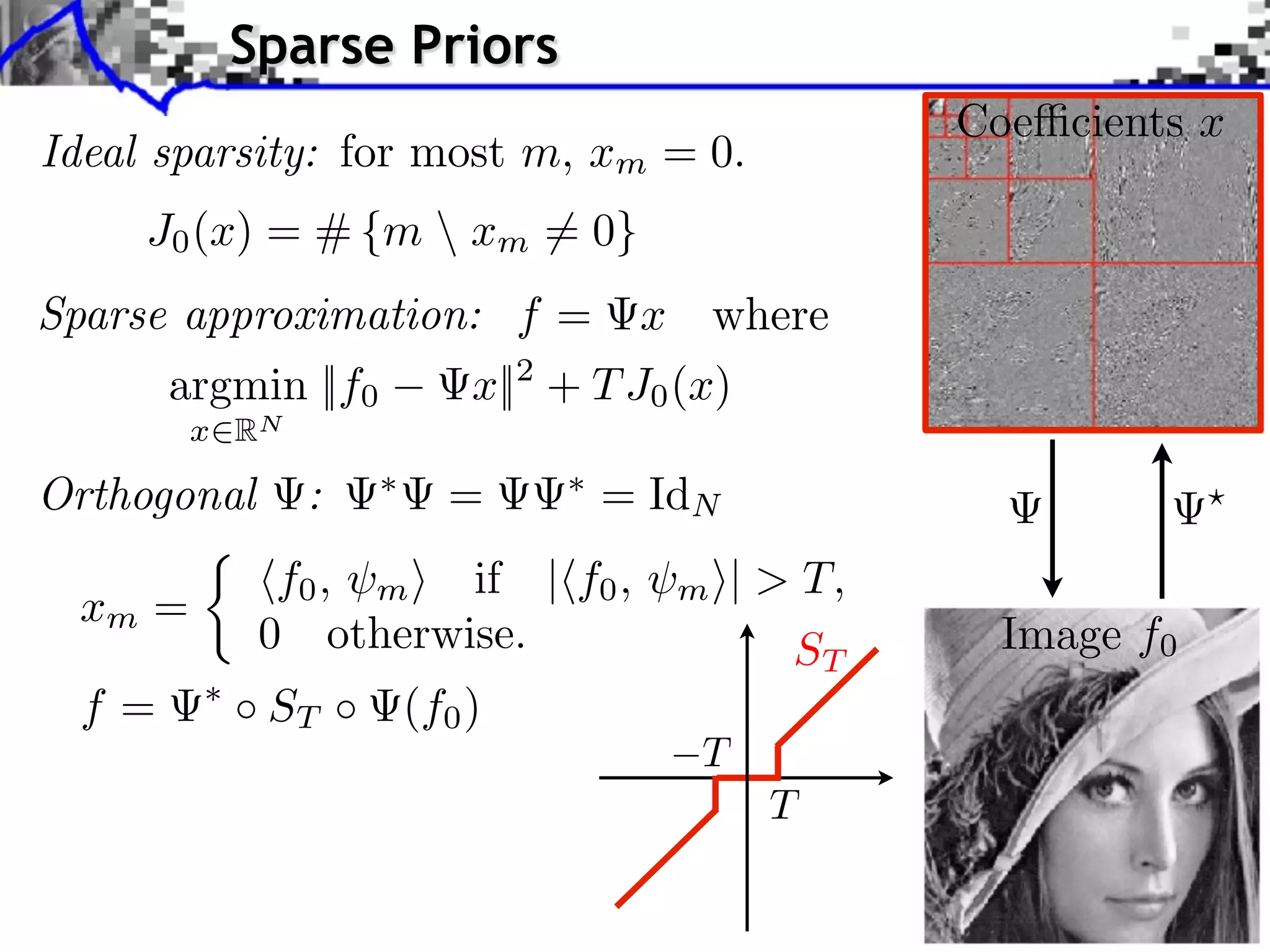
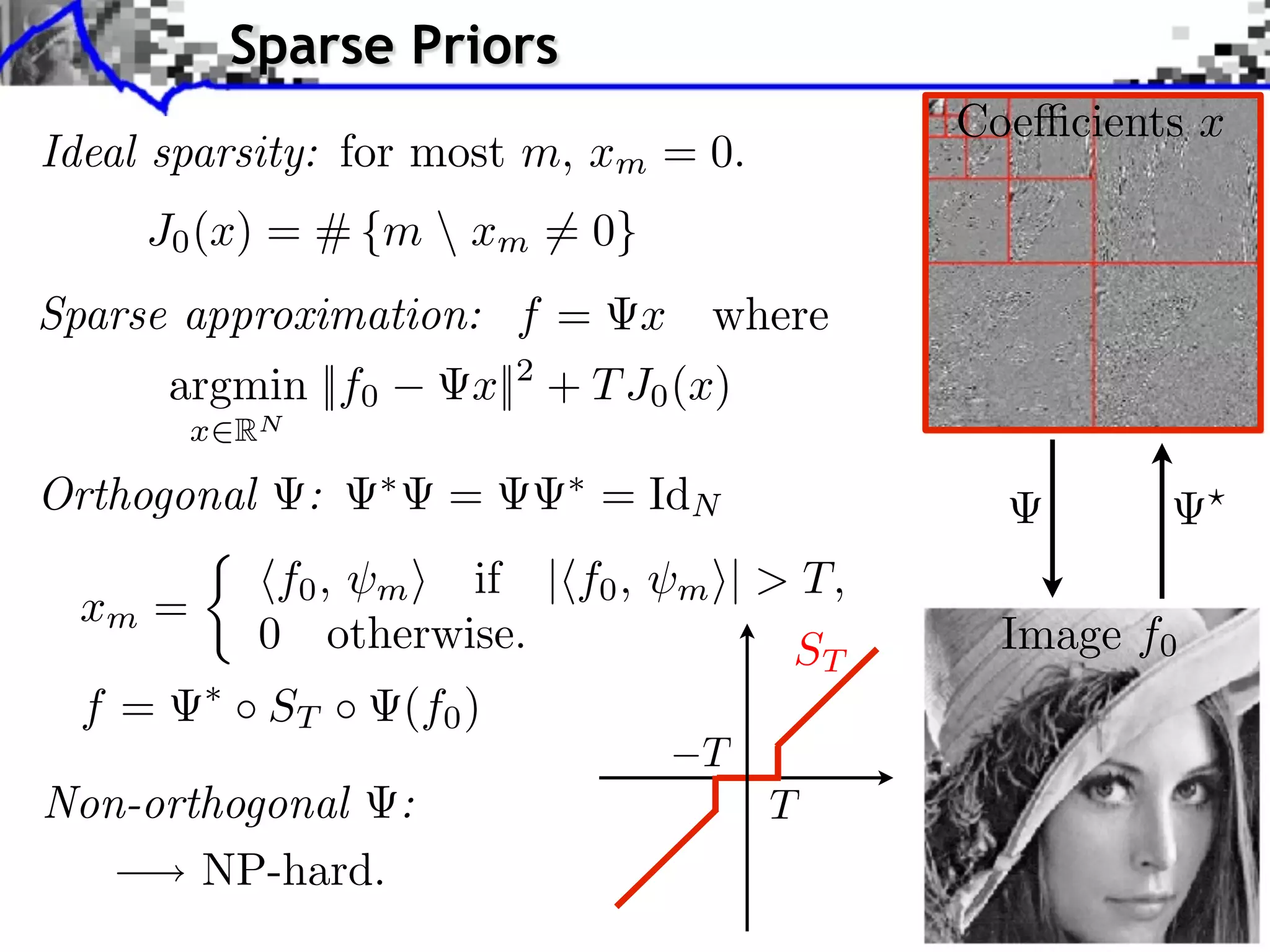
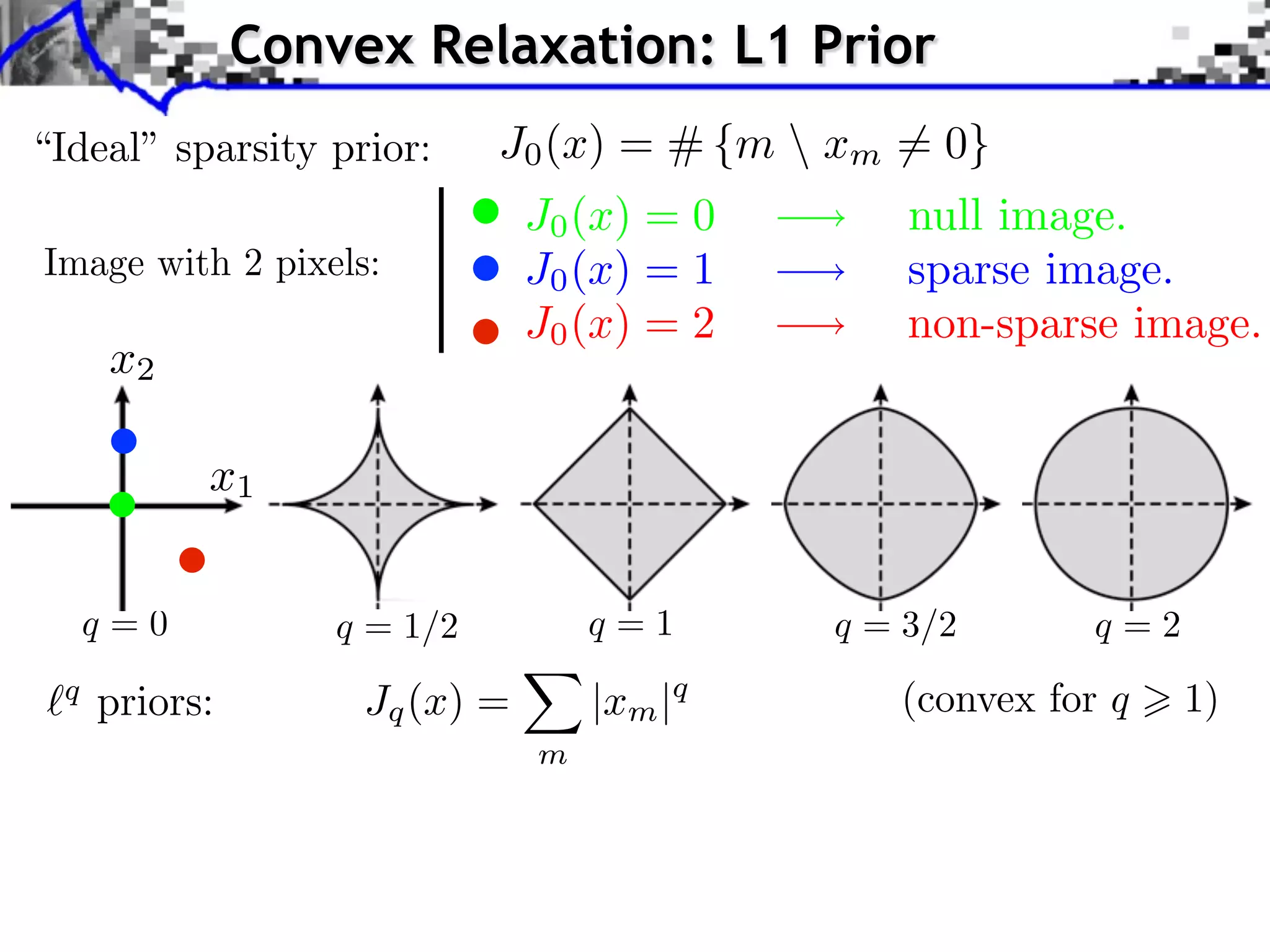
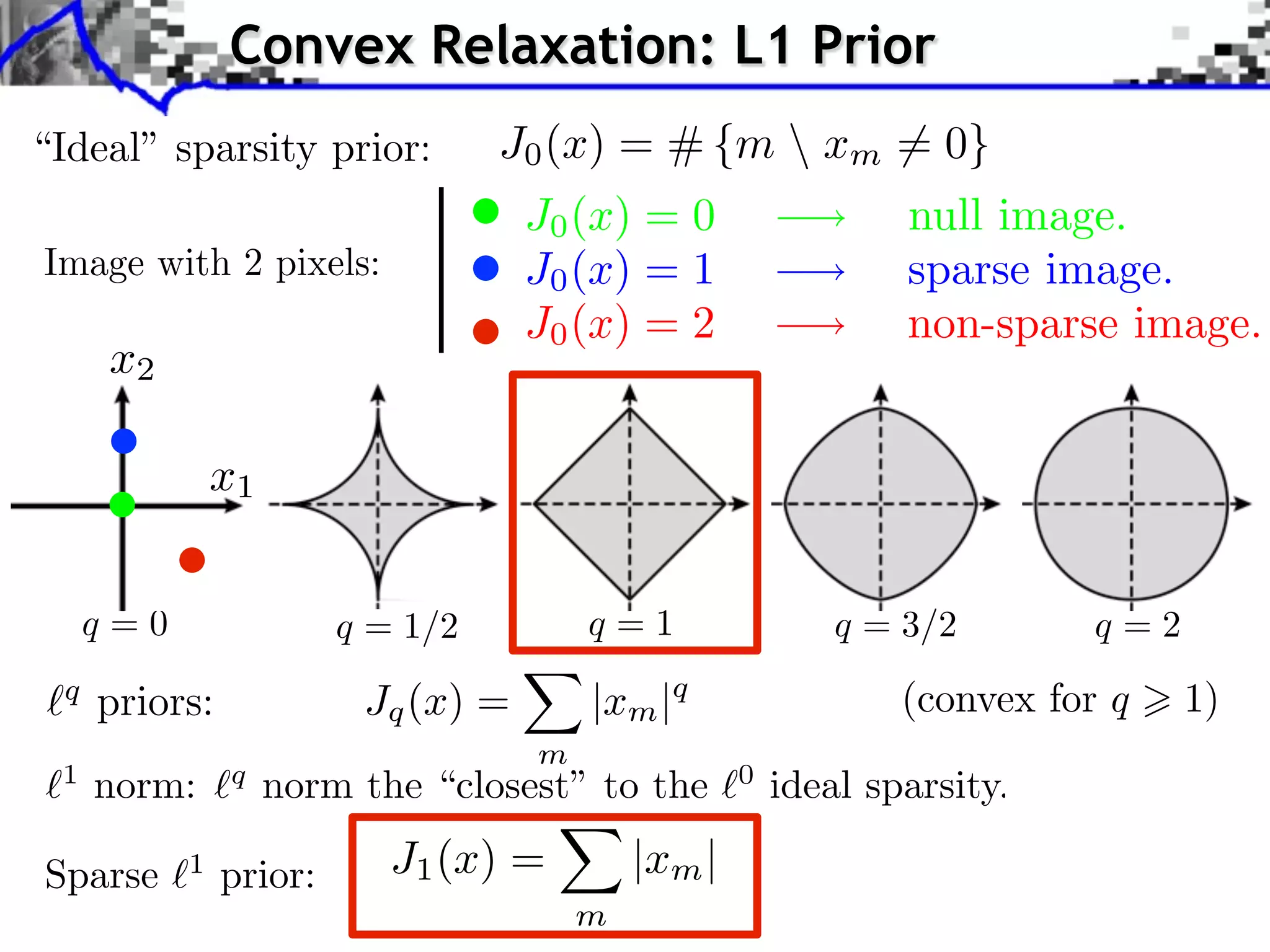
The document discusses inverse problems in the context of sparse synthesis regularization and compressed sensing, outlining key concepts such as theoretical recovery guarantees, data fidelity, and regularization methods. It provides an overview of various techniques for denoising, inpainting, super-resolution, and image separation, alongside the mathematical frameworks and algorithms involved. Additionally, it touches on convex optimization strategies and the use of redundant dictionaries for sparse approximations in image processing.

1. Sparsity and
Compressed Sensing
Gabriel Peyré
www.numerical-tours.com

2. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Theoritical Recovery Guarantees
• Compressed Sensing
• RIP and Polytopes CS Theory
• Fourier Measurements
• Convex Optimization via Proximal Splitting

3. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input

4. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.

5. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.
Inpainting: set of missing pixels, P = Q | |.
0 if x ,
(Kf )(x) =
f (x) if x / .
K

6. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.
Inpainting: set of missing pixels, P = Q | |.
0 if x ,
(Kf )(x) =
f (x) if x / .
Super-resolution: Kf = (f k) , P = Q/ .
K K

7. Inverse Problem in Medical Imaging
Kf = (p k )1 k K

8. Inverse Problem in Medical Imaging
Kf = (p k )1 k K
Magnetic resonance imaging (MRI): ˆ
Kf = (f ( ))
ˆ
f

9. Inverse Problem in Medical Imaging
Kf = (p k )1 k K
Magnetic resonance imaging (MRI): ˆ
Kf = (f ( ))
ˆ
f
Other examples: MEG, EEG, . . .

10. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2

11. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity

12. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity
Choice of : tradeo
Noise level Regularity of f0
||w|| J(f0 )

13. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity
Choice of : tradeo
Noise level Regularity of f0
||w|| J(f0 )
No noise: 0+ , minimize f argmin J(f )
f RQ ,Kf =y

14. Smooth and Cartoon Priors
J(f ) = || f (x)||2 dx
| f |2

15. Smooth and Cartoon Priors
J(f ) = || f (x)||2 dx
J(f ) = || f (x)||dx
J(f ) = length(Ct )dt
R
| f |2 | f|

16. Inpainting Example
Input y = Kf0 + w Sobolev Total variation

17. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Theoritical Recovery Guarantees
• Compressed Sensing
• RIP and Polytopes CS Theory
• Fourier Measurements
• Convex Optimization via Proximal Splitting

18. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
Q
N

19. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
Fourier: m = ei ·, m
frequency
Q
N

20. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
m = (j, , n)
Fourier: m =e i ·, m
frequency scale position
Wavelets:
m = (2 j
R x n) orientation
=1 =2
Q
N

21. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
m = (j, , n)
Fourier: m =e i ·, m
frequency scale position
Wavelets:
m = (2 j
R x n) orientation
DCT, Curvelets, bandlets, . . .
=1 =2
Q
N

22. Redundant Dictionaries
Dictionary =( m )m RQ N
,N Q.
m = (j, , n)
Fourier: m =e i ·, m
frequency scale position
Wavelets:
m = (2 j
R x n) orientation
DCT, Curvelets, bandlets, . . .
Synthesis: f = m xm m = x. =1 =2
Q =f
x
N
Coe cients x Image f = x

23. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Image f0

24. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Sparse approximation: f = x where
argmin ||f0 x||2 + T J0 (x)
x RN
Image f0

25. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Sparse approximation: f = x where
argmin ||f0 x||2 + T J0 (x)
x RN
Orthogonal : = = IdN
f0 , m if | f0 , m | > T,
xm =
0 otherwise. ST Image f0
f= ST (f0 )

26. Sparse Priors
Coe cients x
Ideal sparsity: for most m, xm = 0.
J0 (x) = # {m xm = 0}
Sparse approximation: f = x where
argmin ||f0 x||2 + T J0 (x)
x RN
Orthogonal : = = IdN
f0 , m if | f0 , m | > T,
xm =
0 otherwise. ST Image f0
f= ST (f0 )
Non-orthogonal :
NP-hard.

27. Convex Relaxation: L1 Prior
J0 (x) = # {m xm = 0}
J0 (x) = 0 null image.
Image with 2 pixels: J0 (x) = 1 sparse image.
J0 (x) = 2 non-sparse image.
x2
x1
q=0

28. Convex Relaxation: L1 Prior
J0 (x) = # {m xm = 0}
J0 (x) = 0 null image.
Image with 2 pixels: J0 (x) = 1 sparse image.
J0 (x) = 2 non-sparse image.
x2
x1
q=0 q = 1/2 q=1 q = 3/2 q=2
q
priors: Jq (x) = |xm |q (convex for q 1)
m

29. Convex Relaxation: L1 Prior
J0 (x) = # {m xm = 0}
J0 (x) = 0 null image.
Image with 2 pixels: J0 (x) = 1 sparse image.
J0 (x) = 2 non-sparse image.
x2
x1
q=0 q = 1/2 q=1 q = 3/2 q=2
q
priors: Jq (x) = |xm |q (convex for q 1)
m
Sparse 1
prior: J1 (x) = |xm |
m

30. L1 Regularization
x0 RN
coe cients

31. L1 Regularization
x0 RN f0 = x0 RQ
coe cients image

32. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w

33. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w
= K ⇥ ⇥ RP N

34. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w
= K ⇥ ⇥ RP N
Sparse recovery: f = x where x solves
1
min ||y x||2 + ||x||1
x RN 2
Fidelity Regularization

35. Noiseless Sparse Regularization
Noiseless measurements: y = x0
x
x=
y
x argmin |xm |
x=y m

36. Noiseless Sparse Regularization
Noiseless measurements: y = x0
x
x
x= x=
y y
x argmin |xm | x argmin |xm |2
x=y m x=y m

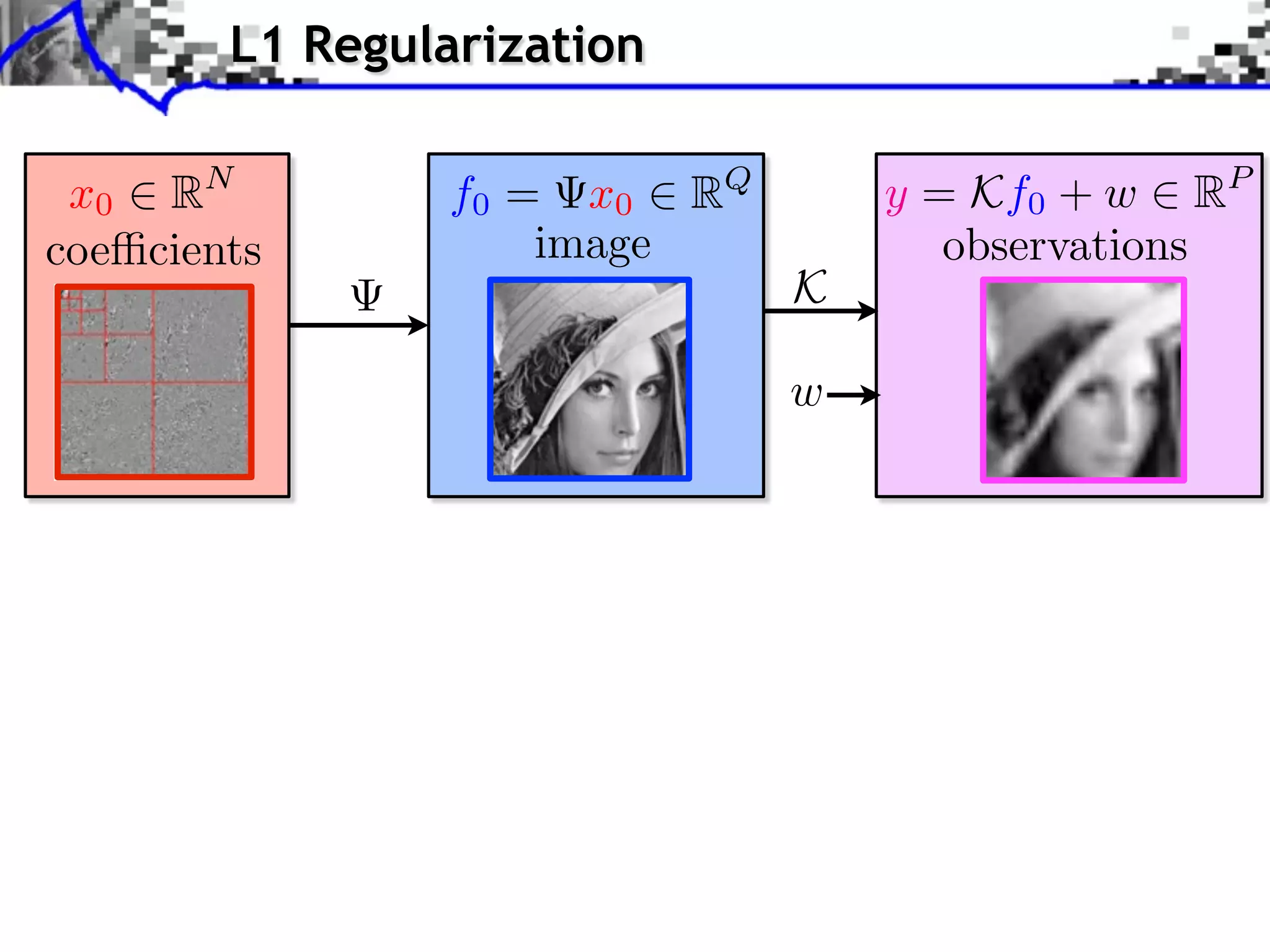
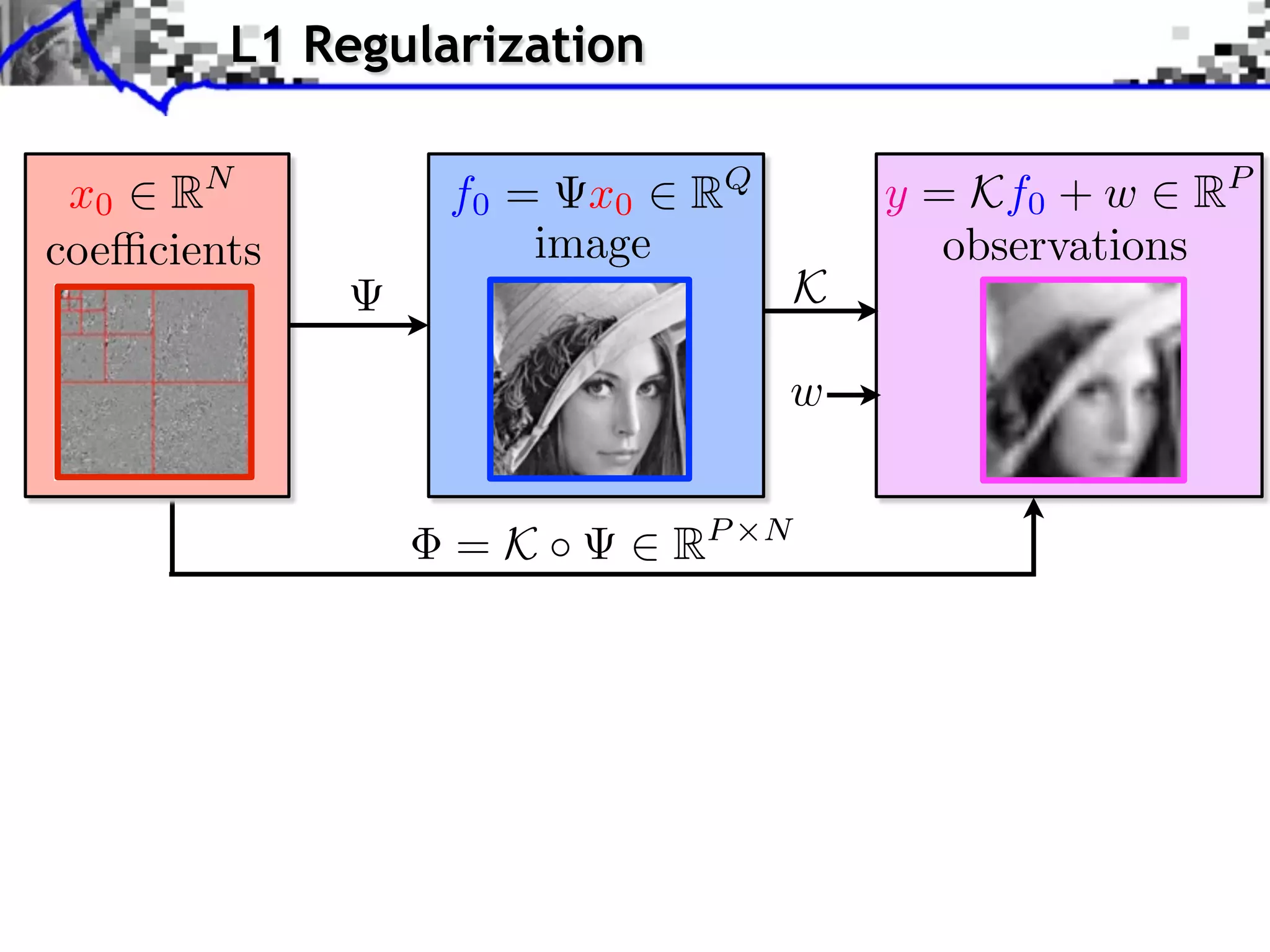
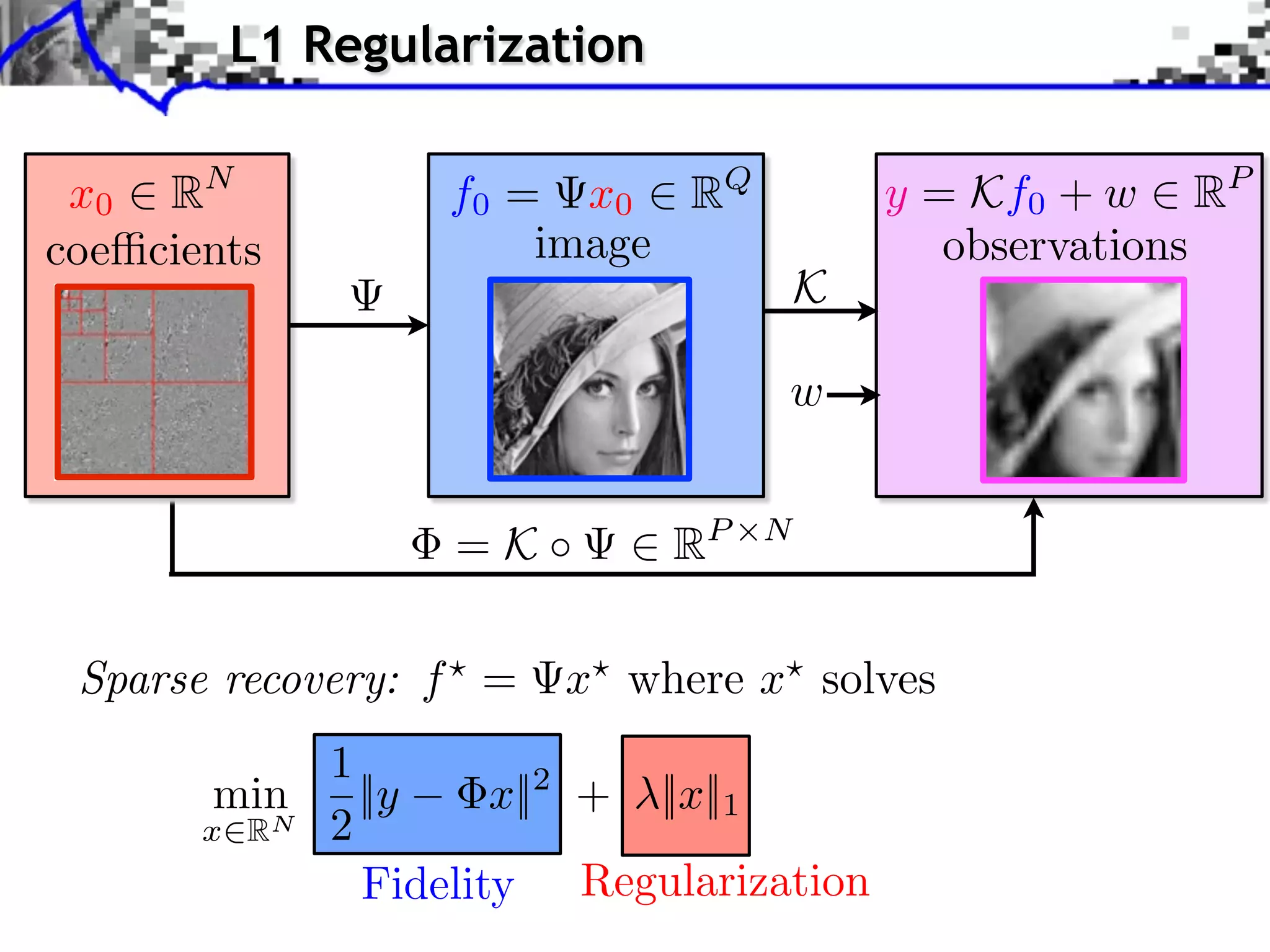
37. Noiseless Sparse Regularization
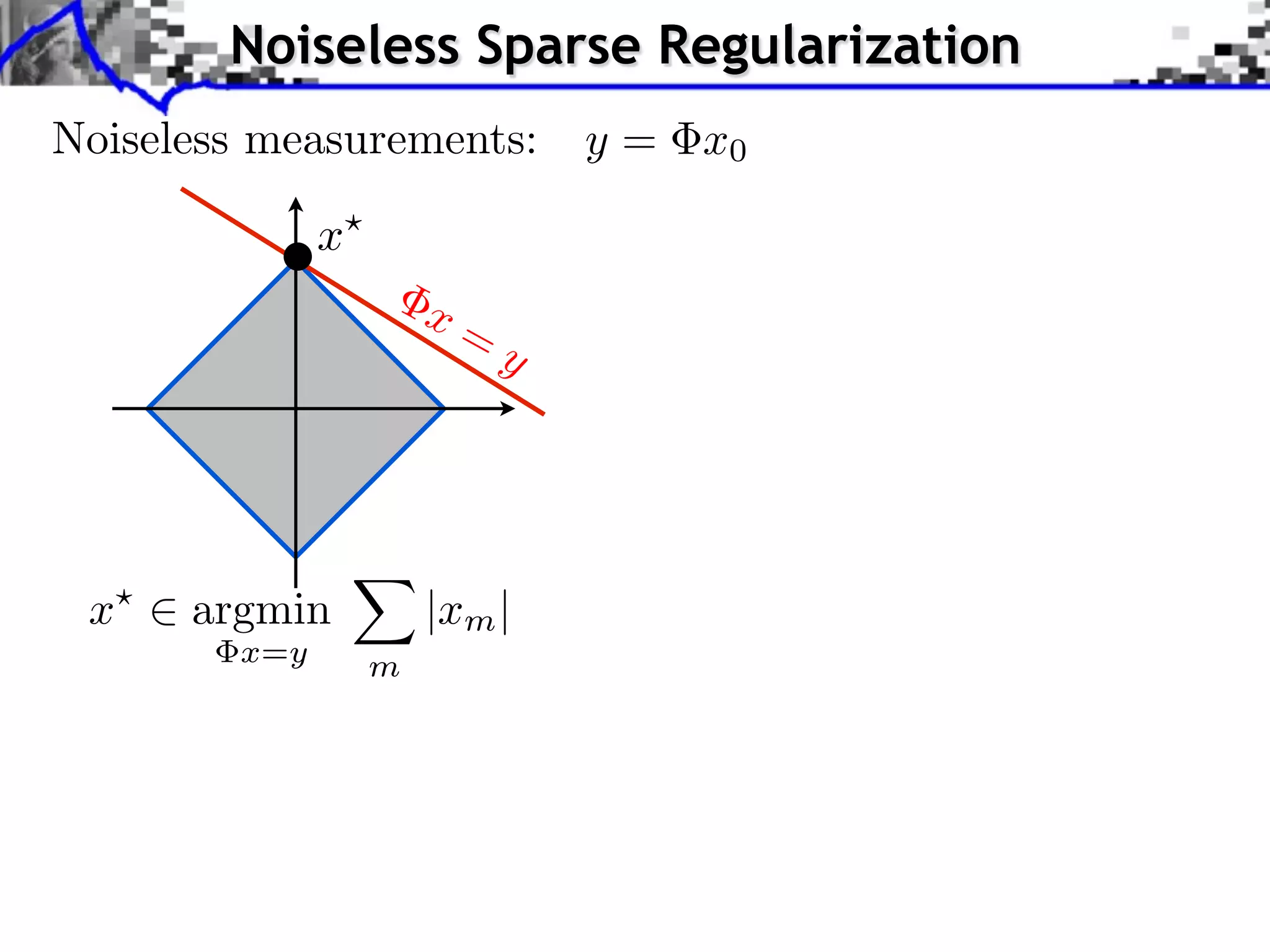
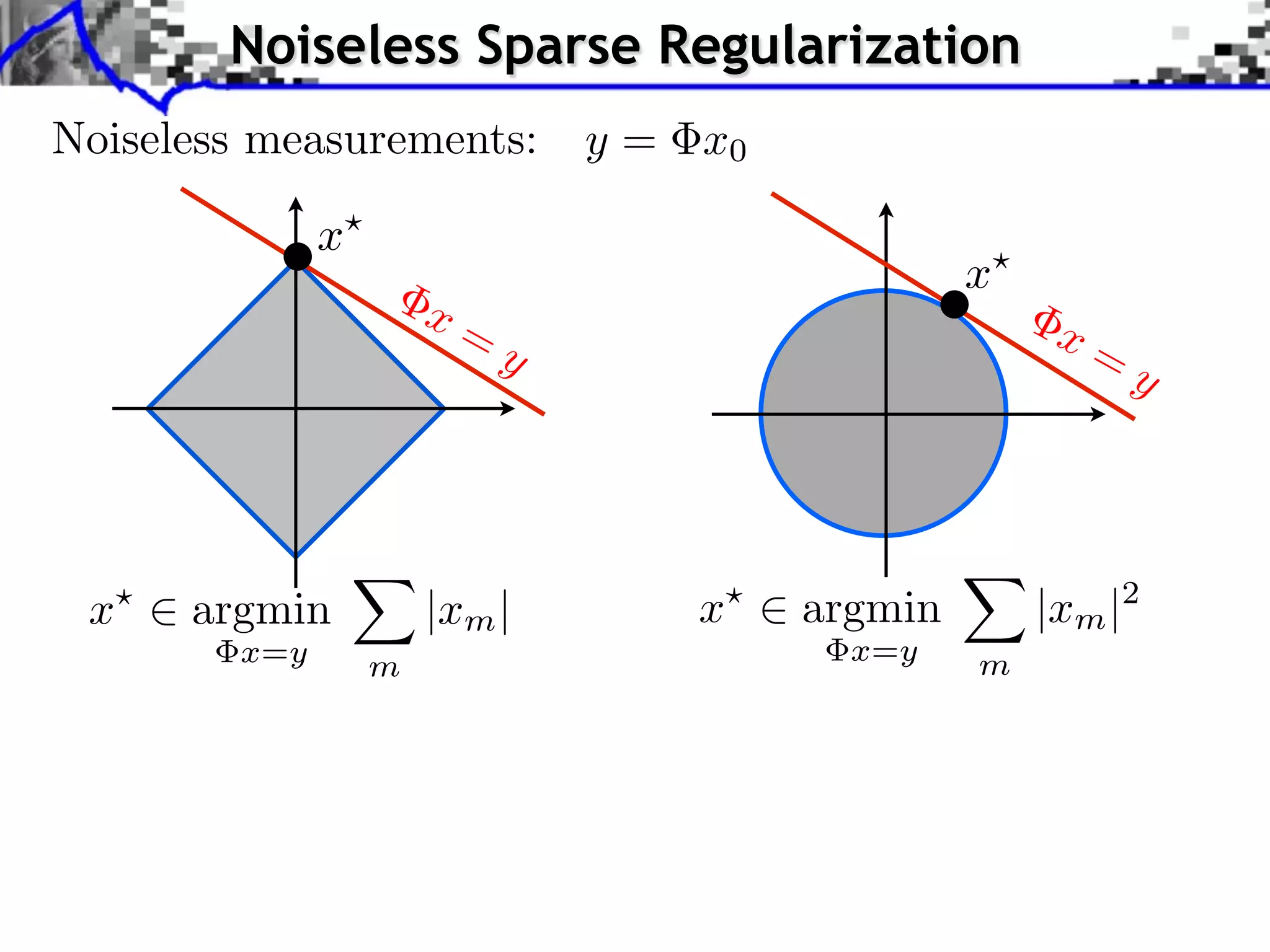
Noiseless measurements: y = x0
x
x
x= x=
y y
x argmin |xm | x argmin |xm |2
x=y m x=y m
Convex linear program.
Interior points, cf. [Chen, Donoho, Saunders] “basis pursuit”.
Douglas-Rachford splitting, see [Combettes, Pesquet].

38. Noisy Sparse Regularization
Noisy measurements: y = x0 + w
1
x argmin ||y x||2 + ||x||1
x RQ 2
Data fidelity Regularization

39. Noisy Sparse Regularization
Noisy measurements: y = x0 + w
1
x argmin ||y x||2 + ||x||1
x RQ 2 Equivalence
Data fidelity Regularization
x argmin ||x||1
|| x y||
|
x=
x y|

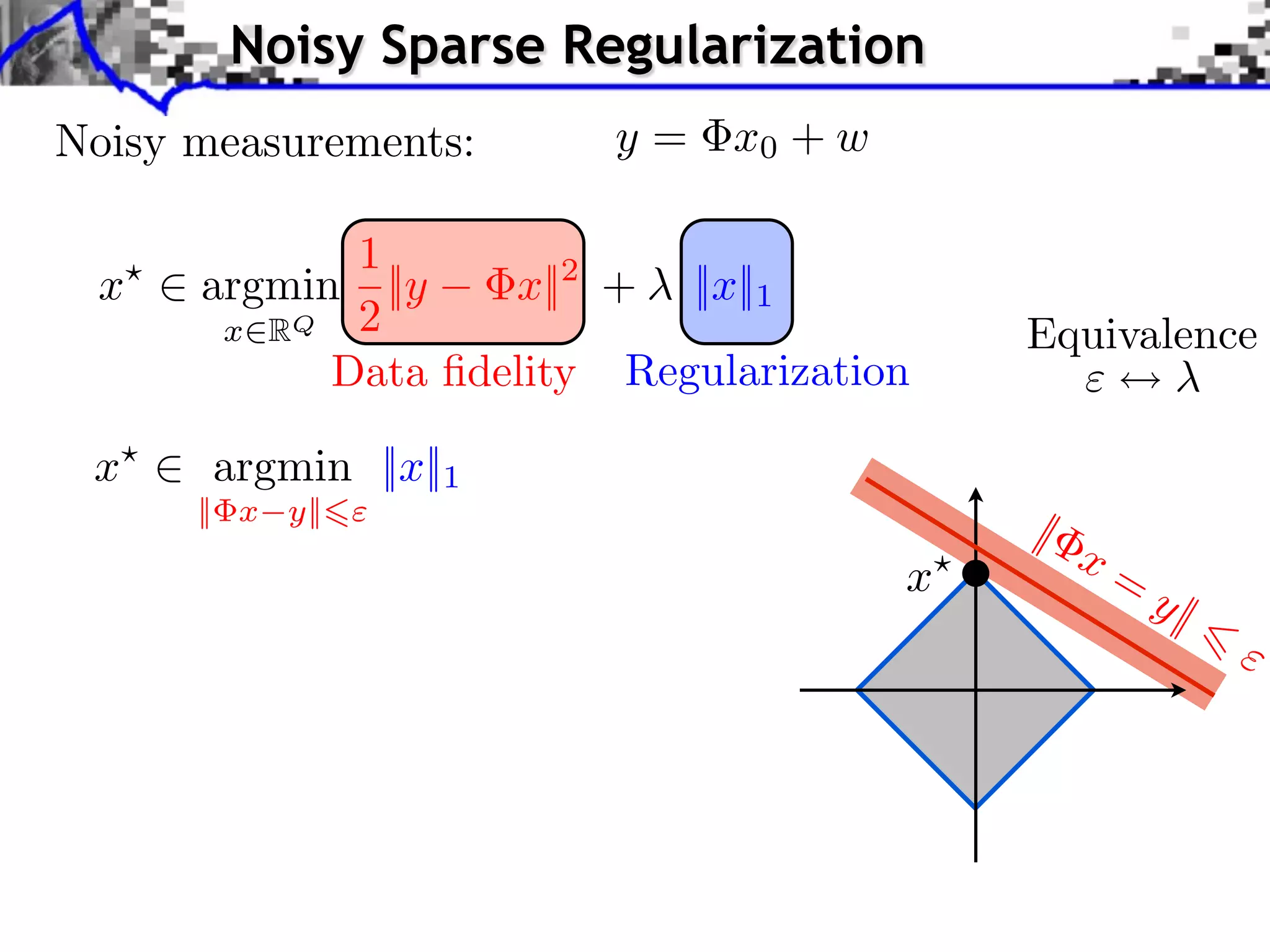
40. Noisy Sparse Regularization
Noisy measurements: y = x0 + w
1
x argmin ||y x||2 + ||x||1
x RQ 2 Equivalence
Data fidelity Regularization
x argmin ||x||1
|| x y||
|
x=
Algorithms: x y|
Iterative soft thresholding
Forward-backward splitting
see [Daubechies et al], [Pesquet et al], etc
Nesterov multi-steps schemes.

41. Image De-blurring
Original f0 y = h f0 + w

42. Image De-blurring
Original f0 y = h f0 + w Sobolev
SNR=22.7dB
Sobolev regularization: f = argmin ||f ⇥ h y||2 + ||⇥f ||2
f RN
ˆ
h(⇥)
ˆ
f (⇥) = y (⇥)
ˆ
ˆ
|h(⇥)|2 + |⇥|2

43. Image De-blurring
Original f0 y = h f0 + w Sobolev Sparsity
SNR=22.7dB SNR=24.7dB
Sobolev regularization: f = argmin ||f ⇥ h y||2 + ||⇥f ||2
f RN
ˆ
h(⇥)
ˆ
f (⇥) = y (⇥)
ˆ
ˆ
|h(⇥)|2 + |⇥|2
Sparsity regularization: = translation invariant wavelets.
1
f = x where x argmin ||h ( x) y||2 + ||x||1
x 2

44. Inpainting Problem
K 0 if x ,
(Kf )(x) =
f (x) if x / .
Measures: y = Kf0 + w

45. Image Separation
Model: f = f1 + f2 + w, (f1 , f2 ) components, w noise.

46. Image Separation
Model: f = f1 + f2 + w, (f1 , f2 ) components, w noise.

47. Image Separation
Model: f = f1 + f2 + w, (f1 , f2 ) components, w noise.
Union dictionary: =[ 1, 2] RQ (N1 +N2 )
Recovered component: fi = i xi .
1
(x1 , x2 ) argmin ||f x||2 + ||x||1
x=(x1 ,x2 ) RN 2

48. Examples of Decompositions

49. Cartoon+Texture Separation

50. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Theoritical Recovery Guarantees
• Compressed Sensing
• RIP and Polytopes CS Theory
• Fourier Measurements
• Convex Optimization via Proximal Splitting

51. Basics of Convex Analysis
Setting: G:H R ⇤ {+⇥} Here: H = RN .
Problem: min G(x)
x H

52. Basics of Convex Analysis
Setting: G:H R ⇤ {+⇥} Here: H = RN .
Problem: min G(x)
x H
Convex: t [0, 1]
x y
G(tx + (1 t)y) tG(x) + (1 t)G(y)

53. Basics of Convex Analysis
Setting: G:H R ⇤ {+⇥} Here: H = RN .
Problem: min G(x)
x H
Convex: t [0, 1]
x y
G(tx + (1 t)y) tG(x) + (1 t)G(y)
Sub-di erential:
G(x) = {u ⇥ H ⇤ z, G(z) G(x) + ⌅u, z x⇧}
G(x) = |x|
G(0) = [ 1, 1]

54. Basics of Convex Analysis
Setting: G:H R ⇤ {+⇥} Here: H = RN .
Problem: min G(x)
x H
Convex: t [0, 1]
x y
G(tx + (1 t)y) tG(x) + (1 t)G(y)
Sub-di erential:
G(x) = {u ⇥ H ⇤ z, G(z) G(x) + ⌅u, z x⇧}
Smooth functions: G(x) = |x|
If F is C 1 , F (x) = { F (x)}
G(0) = [ 1, 1]

55. Basics of Convex Analysis
Setting: G:H R ⇤ {+⇥} Here: H = RN .
Problem: min G(x)
x H
Convex: t [0, 1]
x y
G(tx + (1 t)y) tG(x) + (1 t)G(y)
Sub-di erential:
G(x) = {u ⇥ H ⇤ z, G(z) G(x) + ⌅u, z x⇧}
Smooth functions: G(x) = |x|
If F is C 1 , F (x) = { F (x)}
First-order conditions:
x argmin G(x) 0 G(x ) G(0) = [ 1, 1]
x H

56. L1 Regularization: First Order Conditions
1
x ⇥ argmin G(x) = ||y x||2 + ||x||1
x RQ 2
⇥G(x) = ( x y) + ⇥|| · ||1 (x)
sign(xi ) if xi ⇥= 0,
|| · ||1 (x)i =
[ 1, 1] if xi = 0.

57. L1 Regularization: First Order Conditions
1
x ⇥ argmin G(x) = ||y x||2 + ||x||1
x RQ 2
⇥G(x) = ( x y) + ⇥|| · ||1 (x)
sign(xi ) if xi ⇥= 0,
|| · ||1 (x)i =
[ 1, 1] if xi = 0.
xi
Support of the solution:
i
I = {i ⇥ {0, . . . , N 1} xi ⇤= 0}

58. L1 Regularization: First Order Conditions
1
x ⇥ argmin G(x) = ||y x||2 + ||x||1
x RQ 2
⇥G(x) = ( x y) + ⇥|| · ||1 (x)
sign(xi ) if xi ⇥= 0,
|| · ||1 (x)i =
[ 1, 1] if xi = 0.
xi
Support of the solution:
i
I = {i ⇥ {0, . . . , N 1} xi ⇤= 0}
Restrictions:
xI = (xi )i I R|I| I = ( i )i I RP |I|

59. L1 Regularization: First Order Conditions
1 xi
x argmin || x y||2 + ||x||1 P (y)
x RN 2
i
First order condition:
( x y) + s = 0
sI = sign(xI ),
where
||sI c || 1

60. L1 Regularization: First Order Conditions
1 xi
x argmin || x y||2 + ||x||1 P (y)
x RN 2
i
First order condition:
( x y) + s = 0
i, y x
sI = sign(xI ), i
where
||sI c || 1
1
= sI c = I c (y x )

61. L1 Regularization: First Order Conditions
1 xi
x argmin || x y||2 + ||x||1 P (y)
x RN 2
i
First order condition:
( x y) + s = 0
i, y x
sI = sign(xI ), i
where
||sI c || 1
1
= sI c = I c (y x )
Theorem: || Ic ( x y)|| x solution of P (y)

62. L1 Regularization: First Order Conditions
1 xi
x argmin || x y||2 + ||x||1 P (y)
x RN 2
i
First order condition:
( x y) + s = 0
i, y x
sI = sign(xI ), i
where
||sI c || 1
1
= sI c = I c (y x )
Theorem: || Ic ( x y)|| x solution of P (y)
Theorem: If I has full rank and || I c ( x y)|| <
then x is the unique solution of P (y)

63. Local Behavior of the Solution
1
x argmin || x y||2 + ||x||1
x RN 2
First order condition: ( x y) + s = 0
= xI = +
I y ( I I)
1
sign(xI ) (implicit equation)
= x0,I + +
I w ( I I)
1
sI

64. Local Behavior of the Solution
1
x argmin || x y||2 + ||x||1
x RN 2
First order condition: ( x y) + s = 0
= xI = +
I y ( I I)
1
sign(xI ) (implicit equation)
= x0,I + +
I w ( I I)
1
sI
Intuition: sI = sign(xI ) = sign(x0,I ) = s0,I for small w.
(unknown) (known)

65. Local Behavior of the Solution
1
x argmin || x y||2 + ||x||1
x RN 2
First order condition: ( x y) + s = 0
= xI = +
I y ( I I)
1
sign(xI ) (implicit equation)
= x0,I + +
I w ( I I)
1
sI
Intuition: sI = sign(xI ) = sign(x0,I ) = s0,I for small w.
(unknown) (known)
To prove: xI = x0,I +
ˆ +
I w ( I I)
1
s0,I
is the unique solution.

66. Local Behavior of the Solution
Candidate for the solution:
xI = x0,I +
ˆ +
I w ( I I)
1
s0,I

67. Local Behavior of the Solution
Candidate for the solution:
xI = x0,I +
ˆ +
I w ( I I)
1
s0,I
To prove: || Ic ( ˆ
I xI y)|| <1

68. Local Behavior of the Solution
Candidate for the solution:
xI = x0,I +
ˆ +
I w ( I I)
1
s0,I
To prove: || Ic ( ˆ
I xI y)|| <1
1 w
Ic ( ˆ
I xI y) = I I (s0,I )
+,
I = Ic ( I
+
I Id) I = Ic I

69. Local Behavior of the Solution
Candidate for the solution:
xI = x0,I +
ˆ +
I w ( I I)
1
s0,I
To prove: || Ic ( ˆ
I xI y)|| <1
1 w
Ic ( ˆ
I xI y) = I I (s0,I )
can be made || · || must
small when w 0 be < 1
+,
I = Ic ( I
+
I Id) I = Ic I

70. Robustness to Small Noise
Identifiability crition: [Fuchs]
For s ⇥ { 1, 0, +1}N , let I = supp(s)
F(s) = || I sI || where I = Ic
+,
I

71. Robustness to Small Noise
Identifiability crition: [Fuchs]
For s ⇥ { 1, 0, +1}N , let I = supp(s)
F(s) = || I sI || where I = Ic
+,
I
Theorem: [Fuchs 2004] If F (sign(x0 )) < 1, T = min |x0,i |
i I
If ||w||/T is small enough and ||w||, then
x0,I + +
I w ( I I)
1
sign(x0,I )
is the unique solution of P (y).

72. Robustness to Small Noise
Identifiability crition: [Fuchs]
For s ⇥ { 1, 0, +1}N , let I = supp(s)
F(s) = || I sI || where I = Ic
+,
I
Theorem: [Fuchs 2004] If F (sign(x0 )) < 1, T = min |x0,i |
i I
If ||w||/T is small enough and ||w||, then
x0,I + +
I w ( I I)
1
sign(x0,I )
is the unique solution of P (y).
When w = 0, F (sign(x0 ) < 1 = x = x0 .

73. Robustness to Small Noise
Identifiability crition: [Fuchs]
For s ⇥ { 1, 0, +1}N , let I = supp(s)
F(s) = || I sI || where I = Ic
+,
I
Theorem: [Fuchs 2004] If F (sign(x0 )) < 1, T = min |x0,i |
i I
If ||w||/T is small enough and ||w||, then
x0,I + +
I w ( I I)
1
sign(x0,I )
is the unique solution of P (y).
When w = 0, F (sign(x0 ) < 1 = x = x0 .
Theorem: [Grassmair et al. 2010] If F (sign(x0 )) < 1
if ||w||, ||x x0 || = O(||w||)

74. Geometric Interpretation
+,
dI = sI
F(s) = || I sI || = max | dI , j | I i
j /I
where dI defined by: dI = I( I I)
1
sI
i I, dI , i = si j

75. Geometric Interpretation
+,
dI = sI
F(s) = || I sI || = max | dI , j | I i
j /I
where dI defined by: dI = I( I I)
1
sI
i I, dI , i = si j
Condition F (s) < 1: no vector j inside the cap Cs .
dI
j Cs
i
| dI , ⇥| < 1

76. Geometric Interpretation
+,
dI = sI
F(s) = || I sI || = max | dI , j | I i
j /I
where dI defined by: dI = I( I I)
1
sI
i I, dI , i = si j
Condition F (s) < 1: no vector j inside the cap Cs .
dI
j dI
i k | dI , ⇥| < 1 j Cs
i
| dI , ⇥| < 1

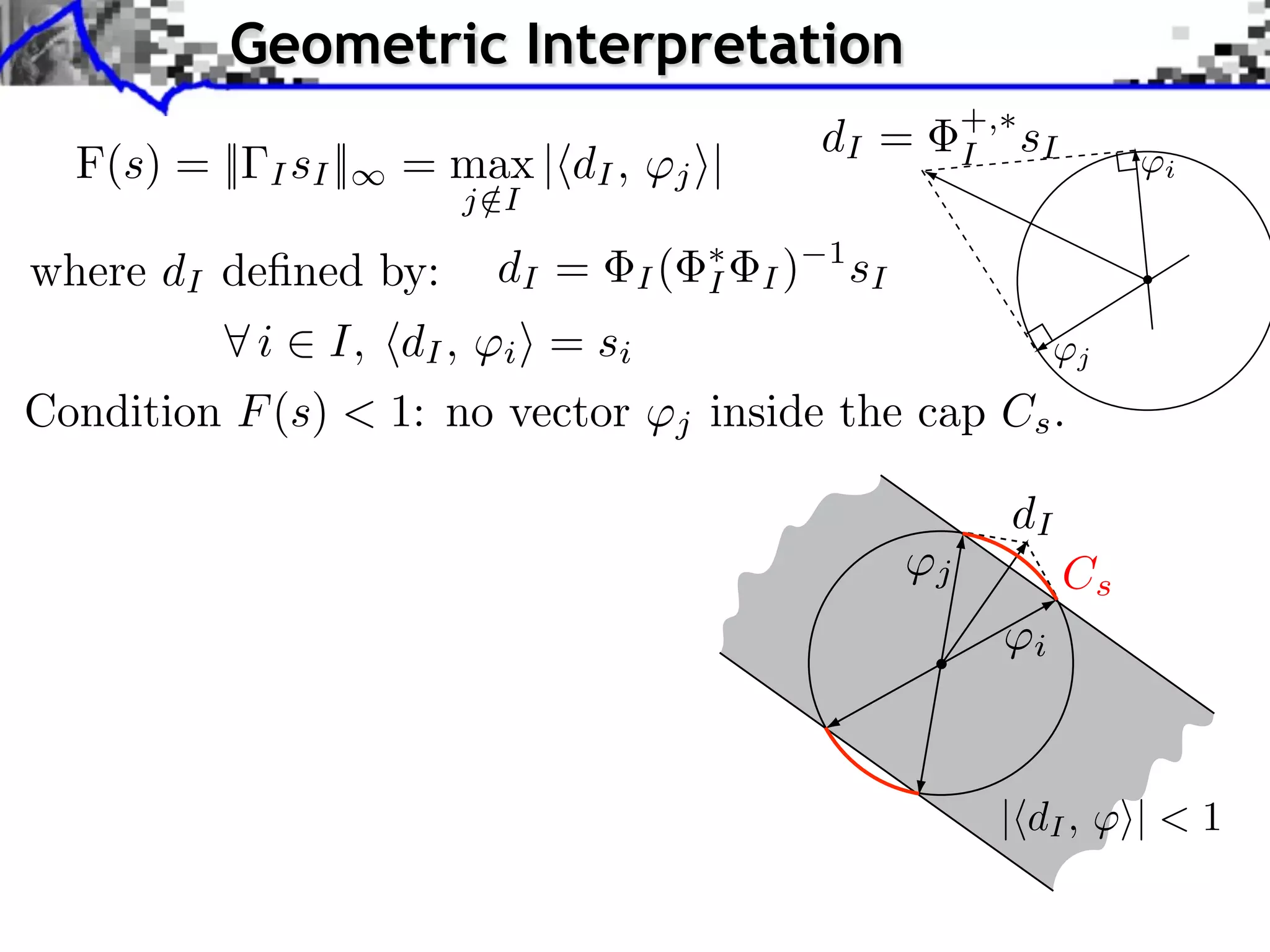
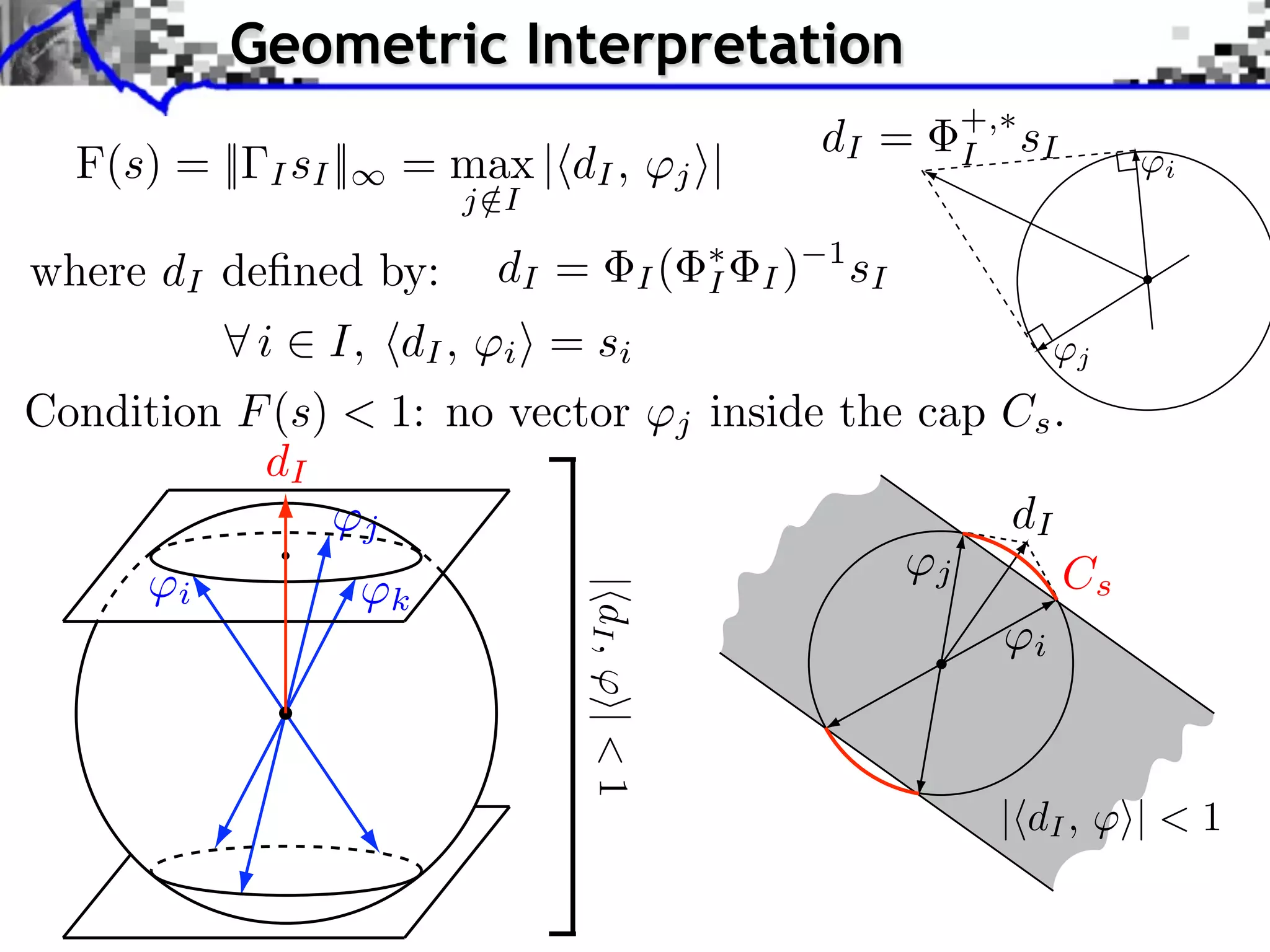
77. Robustness to Bounded Noise
Exact Recovery Criterion (ERC): [Tropp]
For a support I ⇥ {0, . . . , N 1} with I full rank,
ERC(I) = || I || , where I = Ic
+,
I
= || +
I Ic ||1,1 = max ||
c
+
I j ||1
j I
(use ||(aj )j ||1,1 = maxj ||aj ||1 )
Relation with F criterion: ERC(I) = max F(s)
s,supp(s) I

78. Robustness to Bounded Noise
Exact Recovery Criterion (ERC): [Tropp]
For a support I ⇥ {0, . . . , N 1} with I full rank,
ERC(I) = || I || , where I = Ic
+,
I
= || +
I Ic ||1,1 = max ||
c
+
I j ||1
j I
(use ||(aj )j ||1,1 = maxj ||aj ||1 )
Relation with F criterion: ERC(I) = max F(s)
s,supp(s) I
Theorem: If ERC(supp(x0 )) < 1 and ||w||, then
x is unique, satisfies supp(x ) supp(x0 ), and
||x0 x || = O(||w||)

79. Example: Random Matrix
P = 200, N = 1000
1
0.8
0.6
0.4
0.2
0
0 10 20 30 40 50
w-ERC < 1 F <1
ERC < 1 x = x0

80. Example: Deconvolution
⇥x = xi (· i) x0
i
Increasing :
reduces correlation. x0
reduces resolution.
F (s)
ERC(I)
w-ERC(I)

81. Coherence Bounds
Mutual coherence: µ( ) = max | i, j ⇥|
i=j
|I|µ( )
Theorem: F(s) ERC(I) w-ERC(I)
1 (|I| 1)µ( )

82. Coherence Bounds
Mutual coherence: µ( ) = max | i, j ⇥|
i=j
|I|µ( )
Theorem: F(s) ERC(I) w-ERC(I)
1 (|I| 1)µ( )
1 1
Theorem: If ||x0 ||0 < 1+ and ||w||,
2 µ( )
one has supp(x ) I, and ||x0 x || = O(||w||)

83. Coherence Bounds
Mutual coherence: µ( ) = max | i, j ⇥|
i=j
|I|µ( )
Theorem: F(s) ERC(I) w-ERC(I)
1 (|I| 1)µ( )
1 1
Theorem: If ||x0 ||0 < 1+ and ||w||,
2 µ( )
one has supp(x ) I, and ||x0 x || = O(||w||)
N P
One has: µ( )
P (N 1) Optimistic setting:
For Gaussian matrices: ||x0 ||0 O( P )
µ( ) log(P N )/P
For convolution matrices: useless criterion.

84. Spikes and Sinusoids Separation
Incoherent pair of orthobases: Diracs/Fourier
2i
1 = {k ⇤⇥ [k m]}m 2 = k N 1/2
e N mk
m
=[ 1, 2] RN 2N

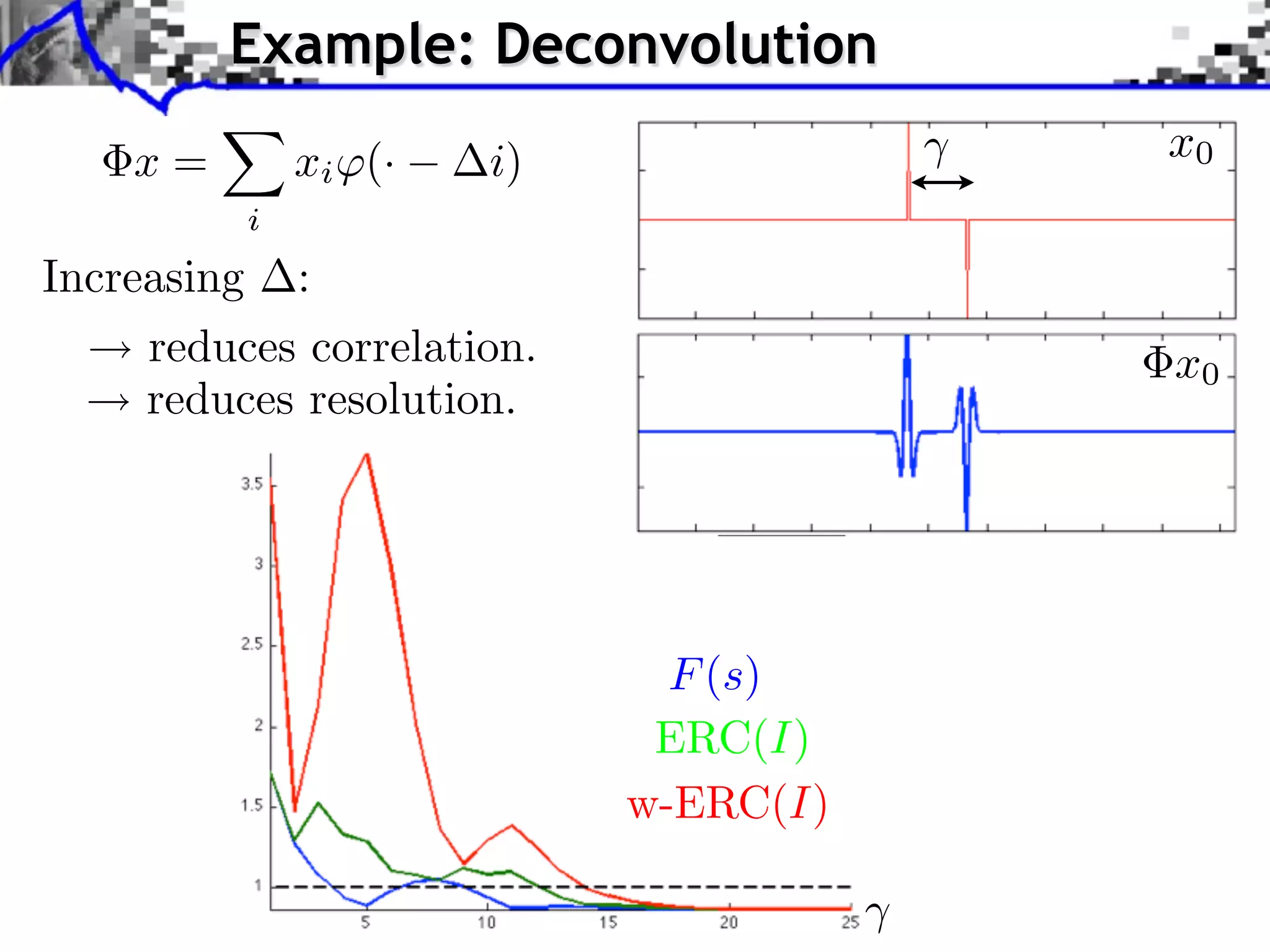
85. Spikes and Sinusoids Separation
Incoherent pair of orthobases: Diracs/Fourier
2i
1 = {k ⇤⇥ [k m]}m 2 = k N 1/2
e N mk
m
=[ 1, 2] RN 2N
1
min ||y x||2 + ||x||1
x R2N 2
1
min ||y 1 x1 2 x2 ||2 + ||x1 ||1 + ||x2 ||1
x1 ,x2 RN 2
= +

86. Spikes and Sinusoids Separation
Incoherent pair of orthobases: Diracs/Fourier
2i
1 = {k ⇤⇥ [k m]}m 2 = k N 1/2
e N mk
m
=[ 1, 2] RN 2N
1
min ||y x||2 + ||x||1
x R2N 2
1
min ||y 1 x1 2 x2 ||2 + ||x1 ||1 + ||x2 ||1
x1 ,x2 RN 2
= +
1
µ( ) = = separates up to N /2 Diracs + sines.
N

87. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Theoritical Recovery Guarantees
• Compressed Sensing
• RIP and Polytopes CS Theory
• Fourier Measurements
• Convex Optimization via Proximal Splitting

88. Pointwise Sampling and Smoothness
Data aquisition: ˜ ˜
f [i] = f (i/N ) = f , i
0
1
Sensors 2
( i )i
(Diracs)
˜
f L2 f RN
ˆ
˜
Shannon interpolation: if Supp(f ) [ N ,N ]

89. Pointwise Sampling and Smoothness
Data aquisition: ˜ ˜
f [i] = f (i/N ) = f , i
0
1
Sensors 2
( i )i
(Diracs)
˜
f L2 f RN
ˆ
˜
Shannon interpolation: if Supp(f ) [ N ,N ]
˜
f (t) = f [i]h(N t i)
i
sin( t)
where h(t) =
t

90. Pointwise Sampling and Smoothness
Data aquisition: ˜ ˜
f [i] = f (i/N ) = f , i
0
1
Sensors 2
( i )i
(Diracs)
˜
f L2 f RN
ˆ
˜
Shannon interpolation: if Supp(f ) [ N ,N ]
˜
f (t) = f [i]h(N t i)
i
sin( t)
where h(t) =
t
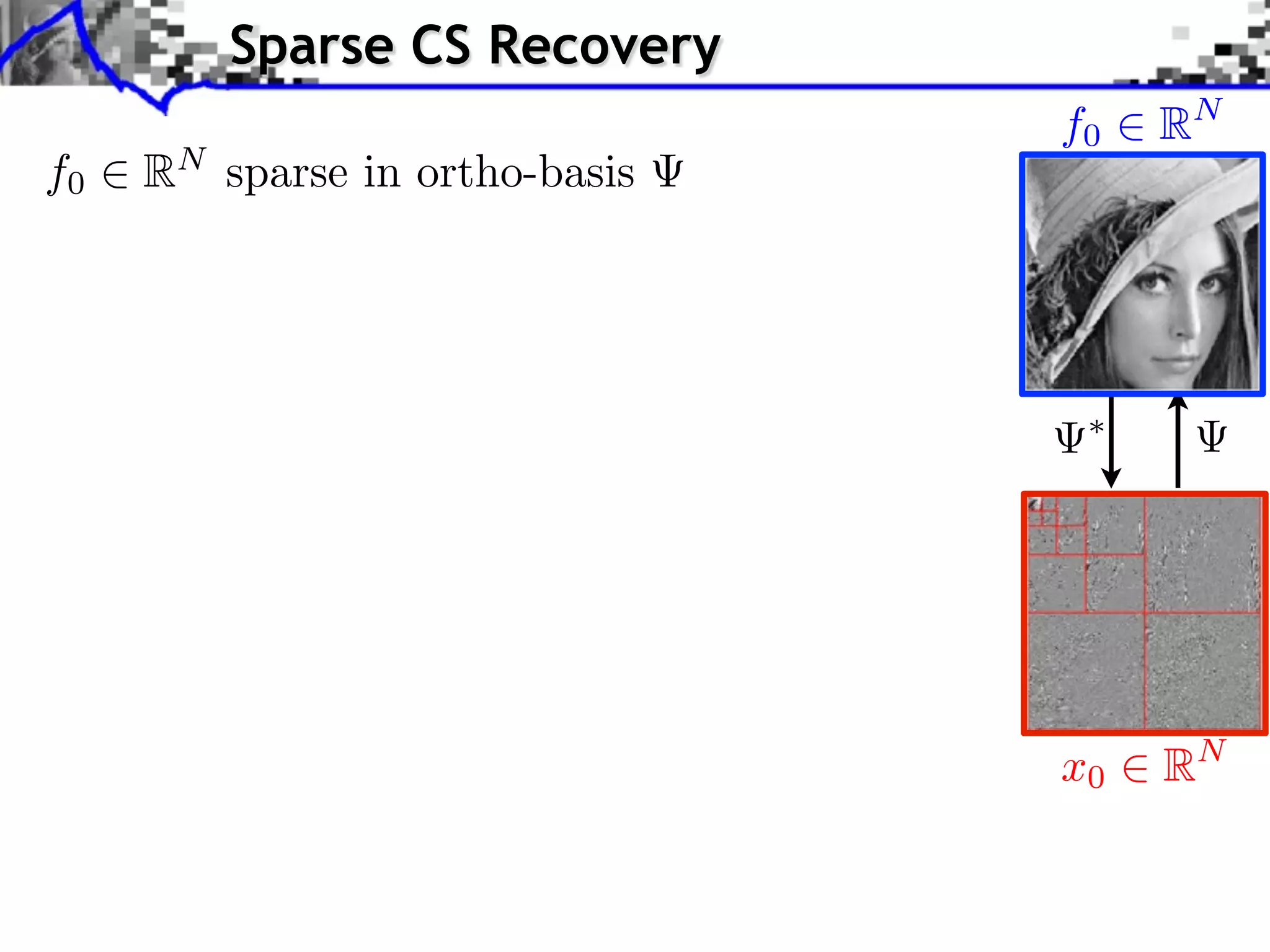
Natural images are not smooth.
But can be compressed e ciently.

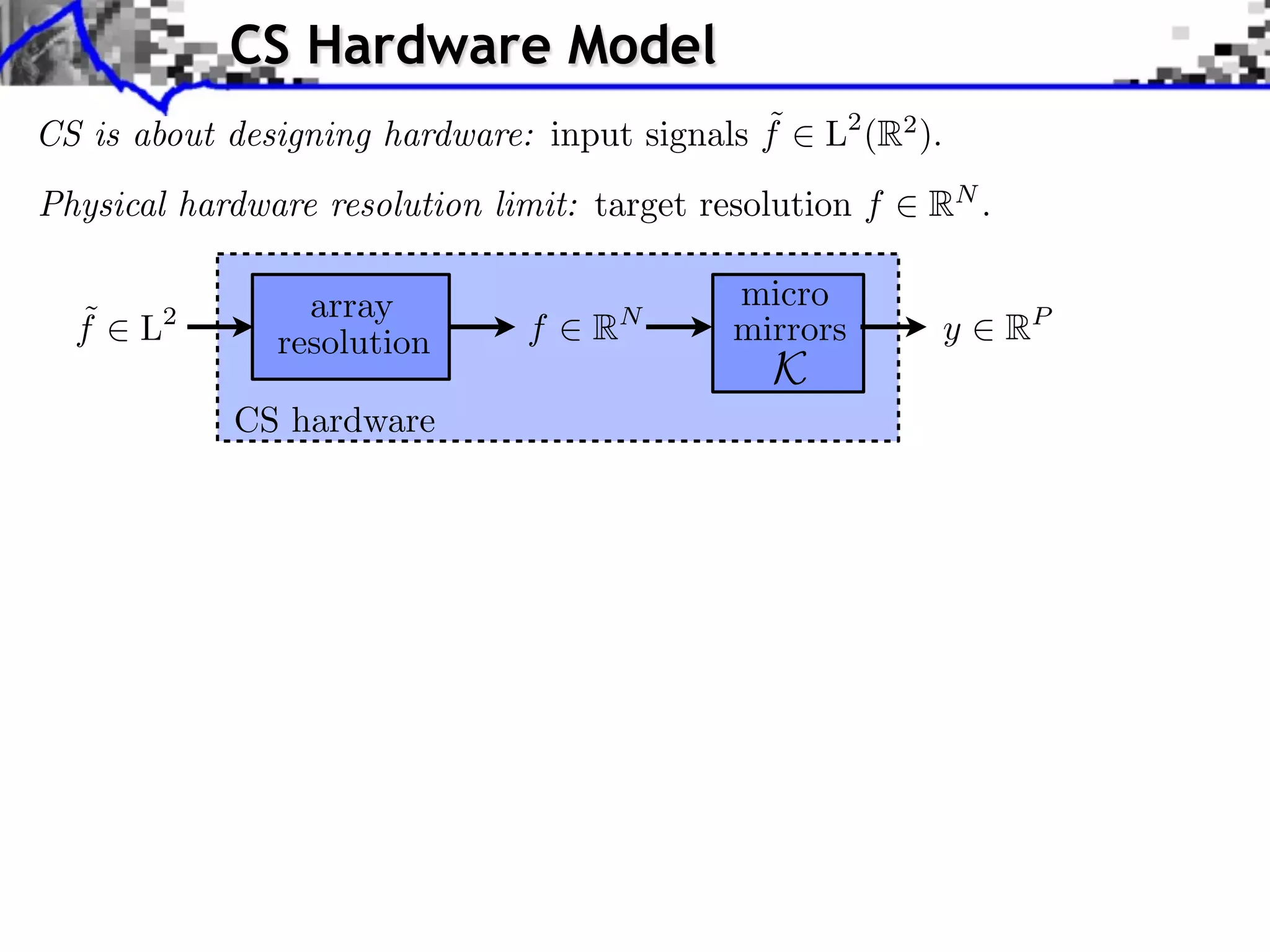
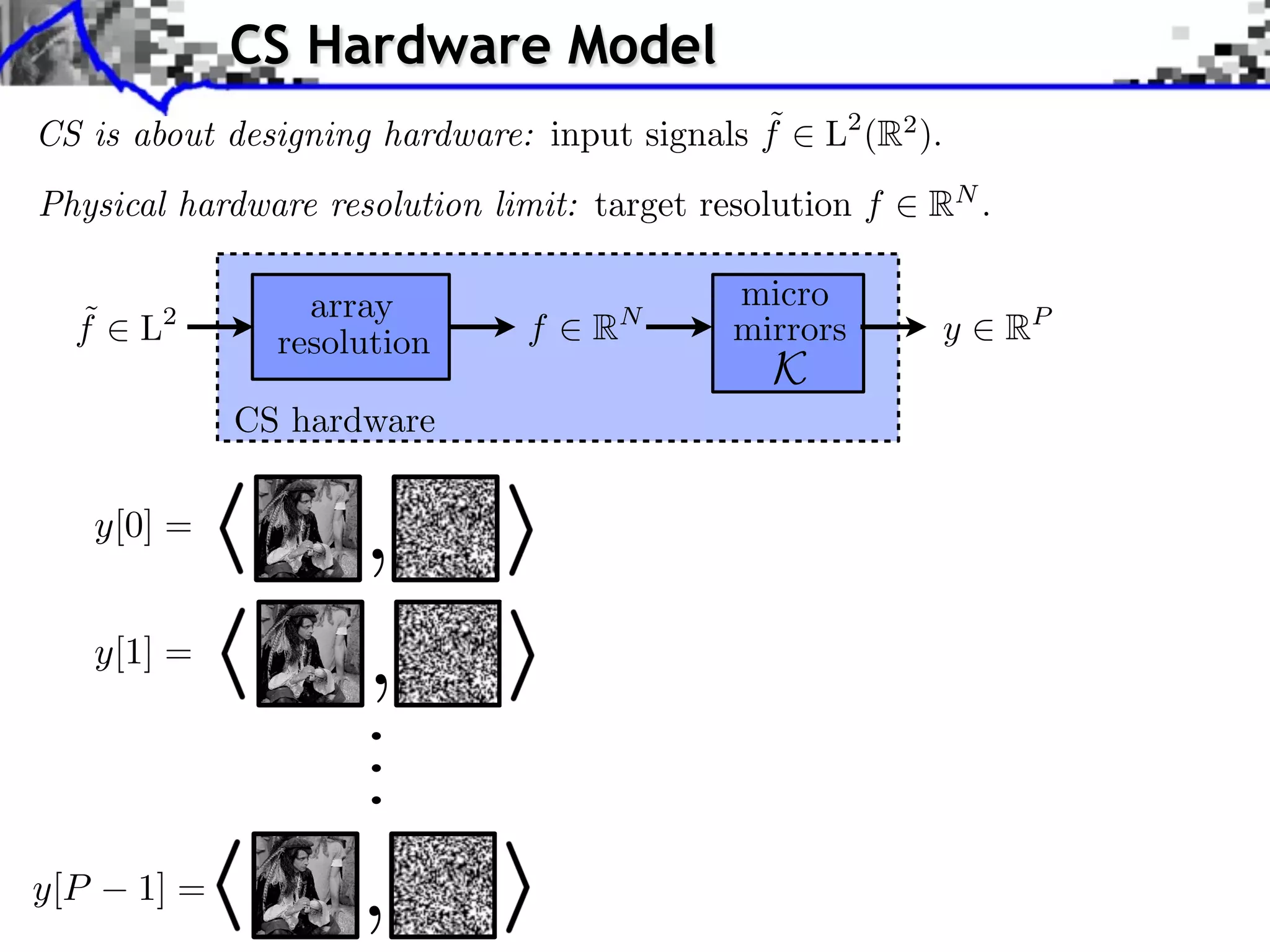
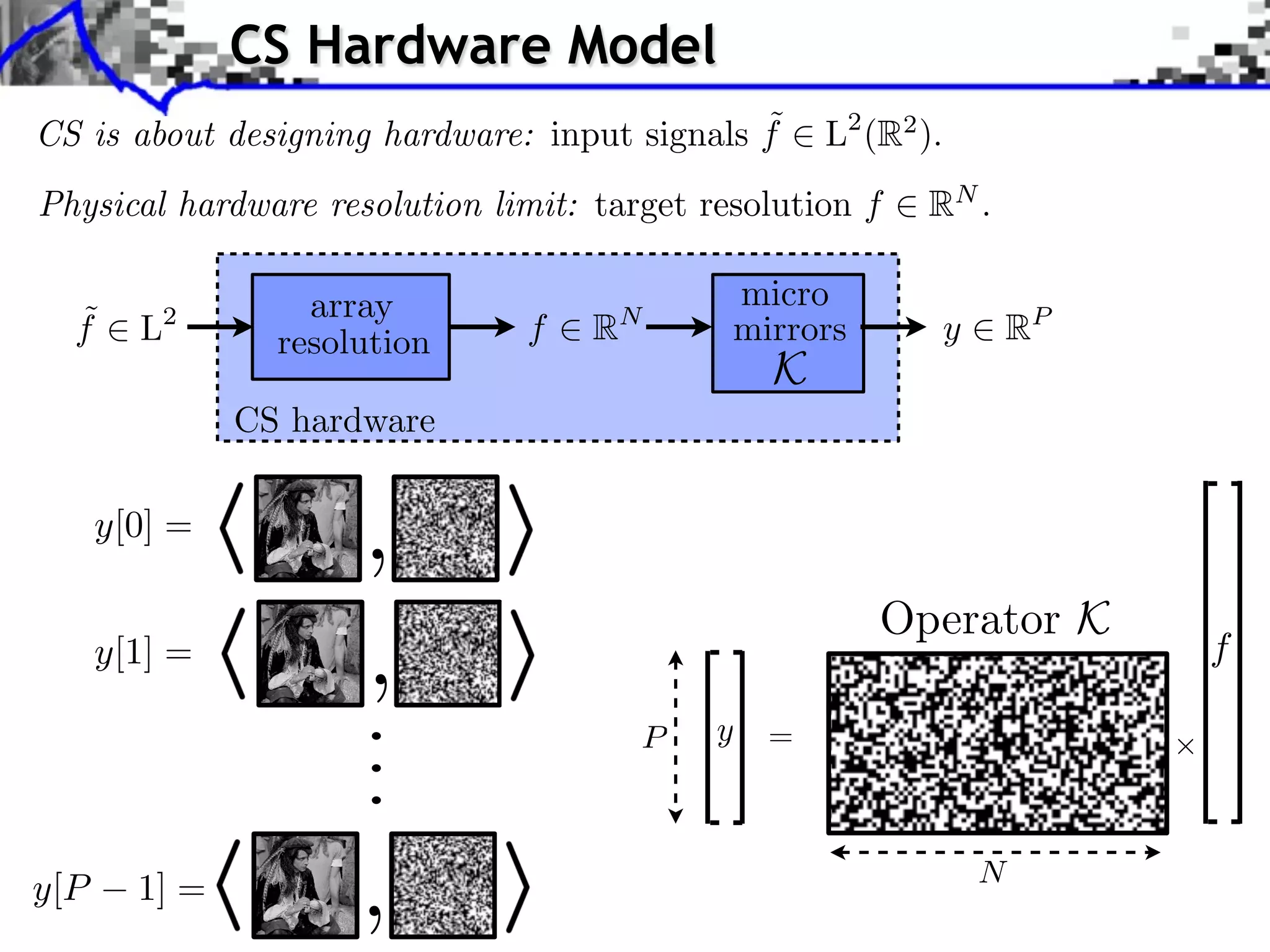
91. Single Pixel Camera (Rice)
y[i] = f0 , i⇥

92. Single Pixel Camera (Rice)
y[i] = f0 , i⇥
f0 , N = 2562 f , P/N = 0.16 f , P/N = 0.02

93. CS Hardware Model
˜
CS is about designing hardware: input signals f L2 (R2 ).
Physical hardware resolution limit: target resolution f RN .
array micro
˜
f L 2
f R N
mirrors y RP
resolution
K
CS hardware

94. CS Hardware Model
˜
CS is about designing hardware: input signals f L2 (R2 ).
Physical hardware resolution limit: target resolution f RN .
array micro
˜
f L 2
f R N
mirrors y RP
resolution
K
CS hardware
,
,
...
,

95. CS Hardware Model
˜
CS is about designing hardware: input signals f L2 (R2 ).
Physical hardware resolution limit: target resolution f RN .
array micro
˜
f L 2
f R N
mirrors y RP
resolution
K
CS hardware
,
Operator K
, f
...
,

96. Sparse CS Recovery
f0 RN
f0 RN sparse in ortho-basis
x0 RN

97. Sparse CS Recovery
f0 RN
f0 RN sparse in ortho-basis
(Discretized) sampling acquisition:
y = Kf0 + w = K (x0 ) + w
=
x0 RN

98. Sparse CS Recovery
f0 RN
f0 RN sparse in ortho-basis
(Discretized) sampling acquisition:
y = Kf0 + w = K (x0 ) + w
=
K drawn from the Gaussian matrix ensemble
Ki,j N (0, P 1/2
) i.i.d.
drawn from the Gaussian matrix ensemble
x0 RN

99. Sparse CS Recovery
f0 RN
f0 RN sparse in ortho-basis
(Discretized) sampling acquisition:
y = Kf0 + w = K (x0 ) + w
=
K drawn from the Gaussian matrix ensemble
Ki,j N (0, P 1/2
) i.i.d.
drawn from the Gaussian matrix ensemble
Sparse recovery: x0 RN
||w|| 1
min ||x||1 min || x y||2 + ||x||1
|| x y|| ||w|| x 2

100. CS Simulation Example
Original f0
= translation invariant
wavelet frame

101. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Theoritical Recovery Guarantees
• Compressed Sensing
• RIP and Polytopes CS Theory
• Fourier Measurements
• Convex Optimization via Proximal Splitting

102. CS with RIP
1
recovery:
y = x0 + w
x⇥ argmin ||x||1 where
|| x y|| ||w||
Restricted Isometry Constants:
⇥ ||x||0 k, (1 k )||x||2 || x||2 (1 + k )||x||2

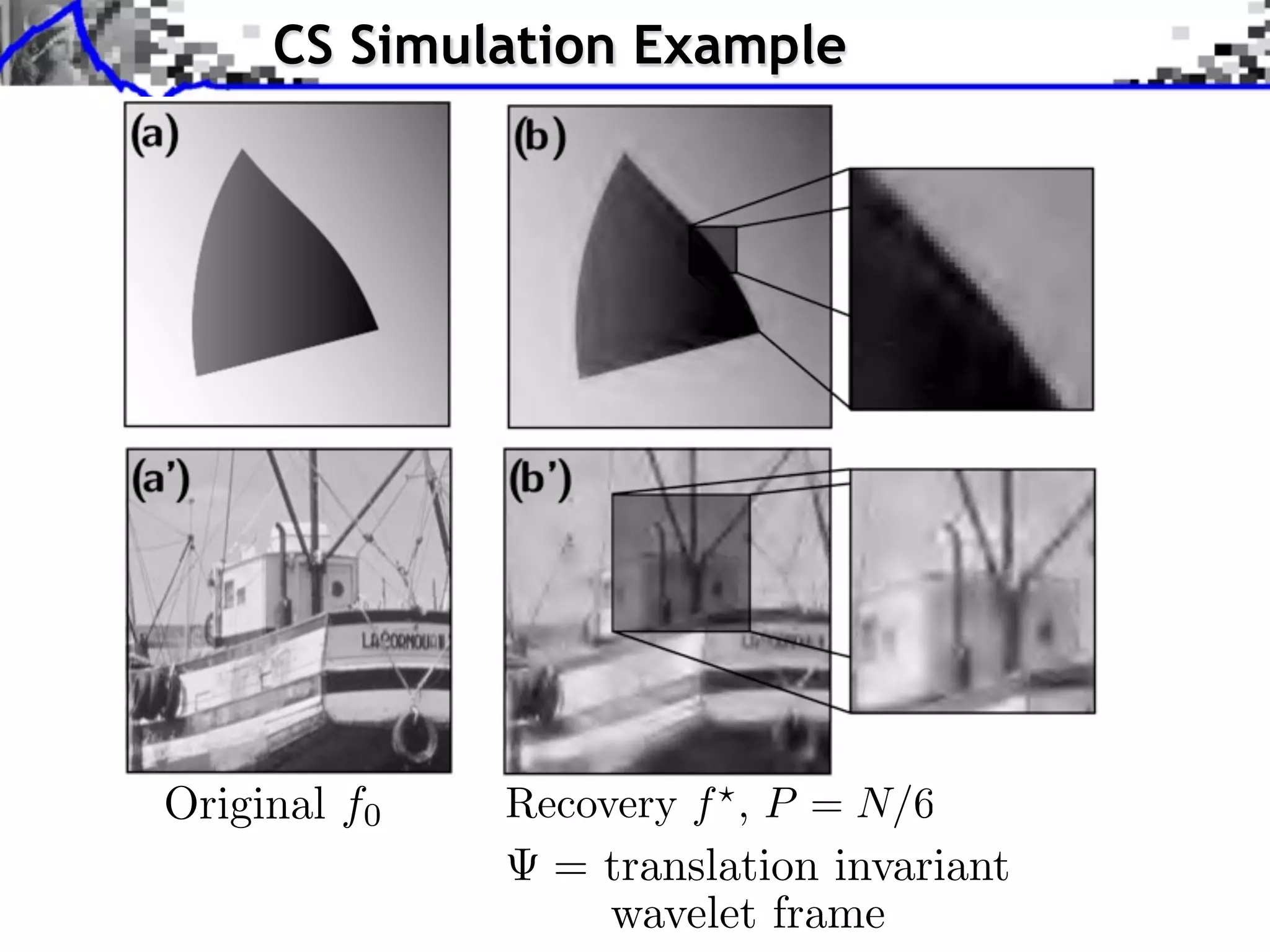
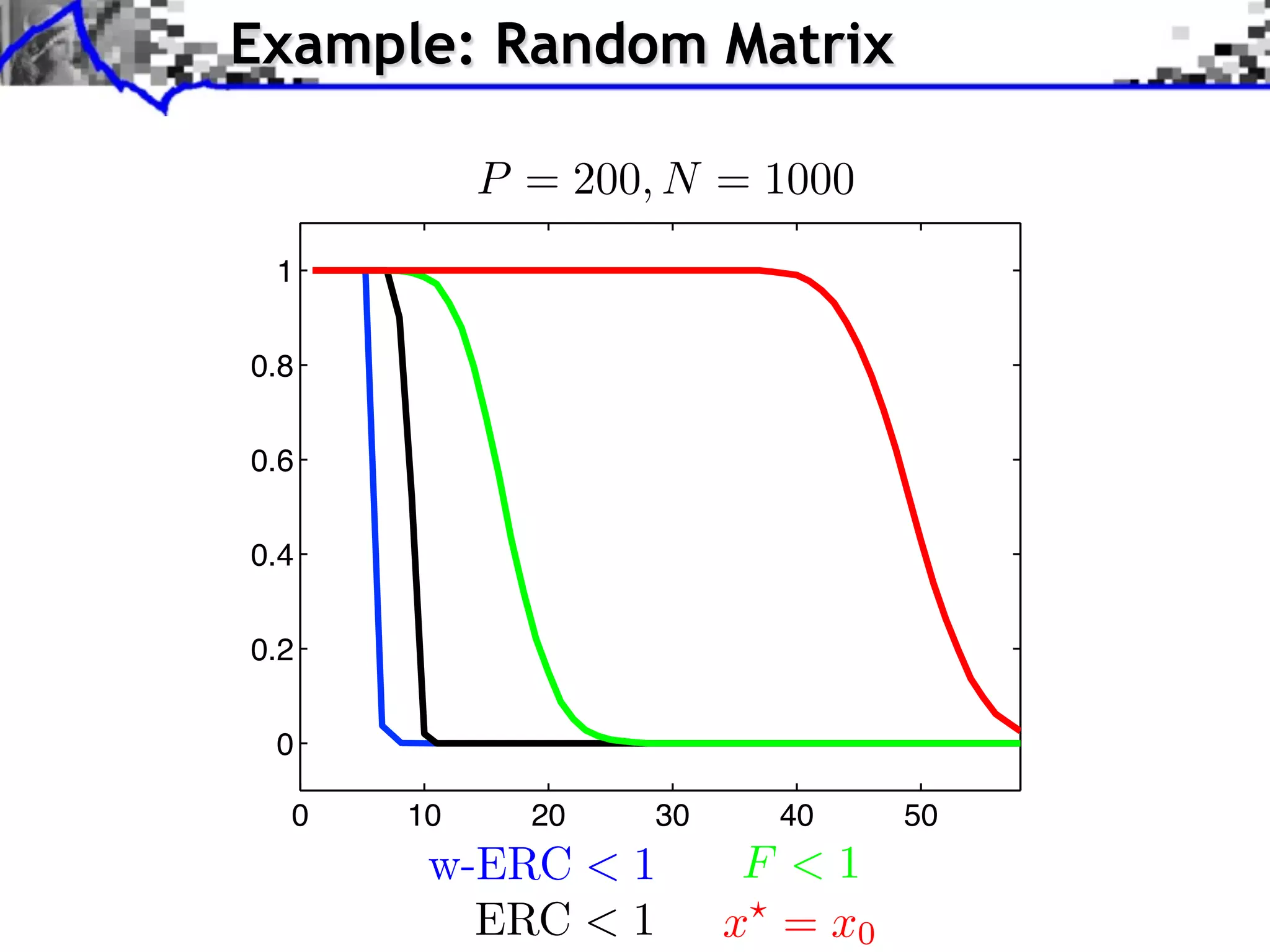
103. CS with RIP
1
recovery:
y = x0 + w
x⇥ argmin ||x||1 where
|| x y|| ||w||
Restricted Isometry Constants:
⇥ ||x||0 k, (1 k )||x||2 || x||2 (1 + k )||x||2
Theorem: If 2k 2 1, then [Candes 2009]
C0
||x0 x || ⇥ ||x0 xk ||1 + C1
k
where xk is the best k-term approximation of x0 .

104. Singular Values Distributions
Eigenvalues of I I with |I| = k are essentially in [a, b]
a = (1 )2 and b = (1 )2 where = k/P
When k = P + , the eigenvalue distribution tends to
1
f (⇥) = (⇥ b)+ (a ⇥)+ [Marcenko-Pastur]
1.5
2⇤ ⇥ P=200, k=10
P=200, k=10
f ( )
1.5
1
1
0.5
P = 200, k = 10
0.5
0
0 0.5 1 1.5 2 2.5
0
0 0.5 1 P=200, k=30 1.5 2 2.5
1
P=200, k=30
0.8
1
0.6
0.8
0.4
k = 30
0.6
0.2
0.4
0
0.2
0 0.5 1 1.5 2 2.5
0
0 0.5 1 P=200, k=50 1.5 2 2.5
P=200, k=50
0.8
0.8
0.6
0.6
0.4
Large deviation inequality [Ledoux]
0.4
0.2

105. RIP for Gaussian Matrices
Link with coherence: µ( ) = max | i, j ⇥|
i=j
2 = µ( )
k (k 1)µ( )

106. RIP for Gaussian Matrices
Link with coherence: µ( ) = max | i, j ⇥|
i=j
2 = µ( )
k (k 1)µ( )
For Gaussian matrices:
µ( ) log(P N )/P

107. RIP for Gaussian Matrices
Link with coherence: µ( ) = max | i, j ⇥|
i=j
2 = µ( )
k (k 1)µ( )
For Gaussian matrices:
µ( ) log(P N )/P
Stronger result:
C
Theorem: If k P
log(N/P )
then 2k 2 1 with high probability.

108. Numerics with RIP
Stability constant of A:
(1 ⇥1 (A))|| ||2 ||A ||2 (1 + ⇥2 (A))|| ||2
smallest / largest eigenvalues of A A

109. Numerics with RIP
Stability constant of A:
(1 ⇥1 (A))|| ||2 ||A ||2 (1 + ⇥2 (A))|| ||2
smallest / largest eigenvalues of A A
Upper/lower RIC:
ˆ2
k
i
k = max i( I)
|I|=k
2 1 ˆ2
k
k = min( k, k)
1 2
Monte-Carlo estimation:
ˆk k k
N = 4000, P = 1000

110. Polytopes-based Guarantees
Noiseless recovery: x argmin ||x||1 (P0 (y))
x=y
= ( i )i R2 3
3 2
1
x0 x0
1
y x
3
B = {x ||x||1 } 2
(B )
= ||x0 ||1

111. Polytopes-based Guarantees
Noiseless recovery: x argmin ||x||1 (P0 (y))
x=y
= ( i )i R2 3
3 2
1
x0 x0
1
y x
3
B = {x ||x||1 } 2
(B )
= ||x0 ||1
x0 solution of P0 ( x0 ) ⇥ x0 ⇤ (B )

112. L1 Recovery in 2-D
= ( i )i R2 3
C(0,1,1) 2
3
K(0,1,1)
1
y x
2-D quadrant 2-D cones
Ks = ( i si )i R3 i 0 Cs = Ks

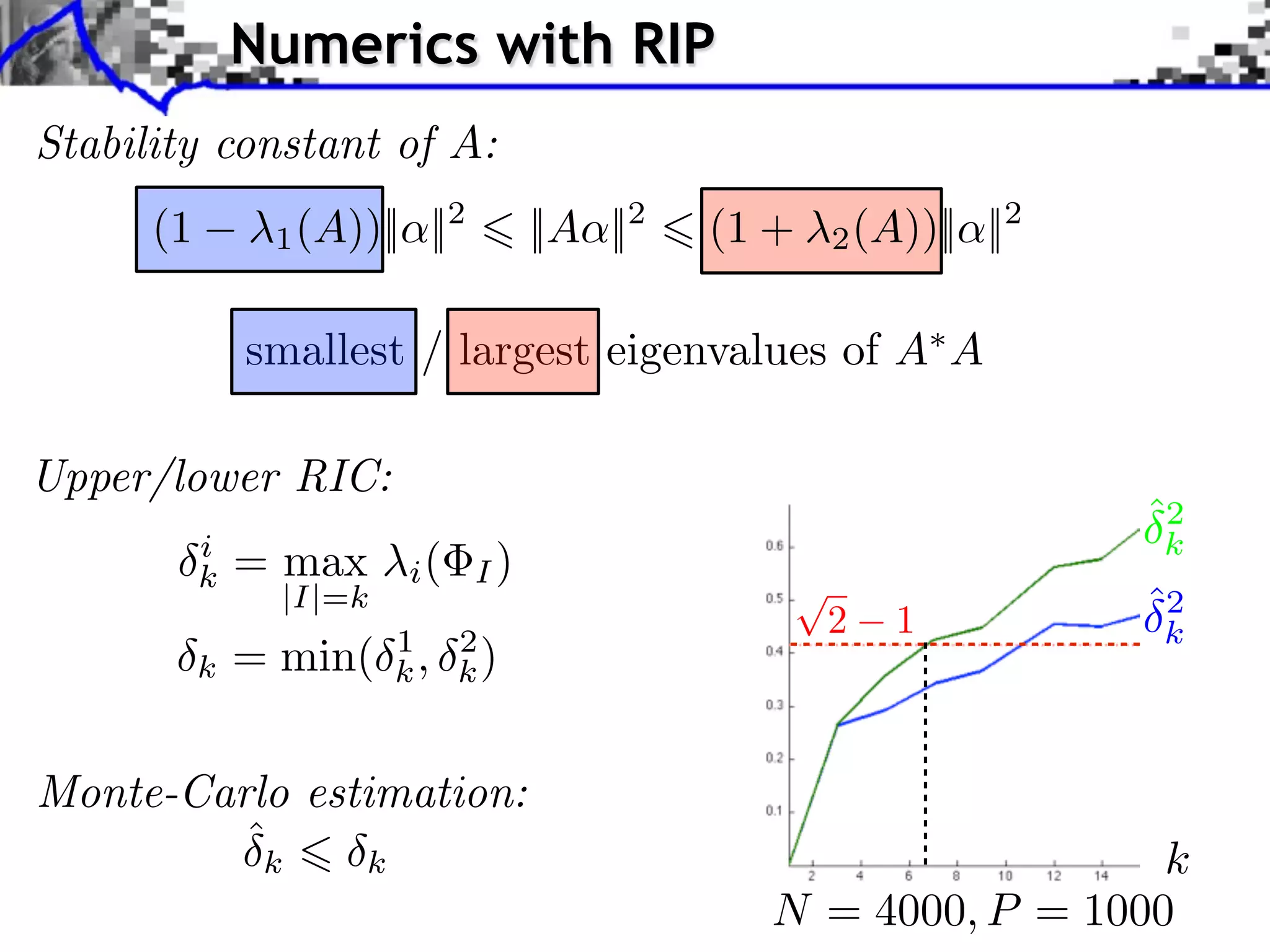
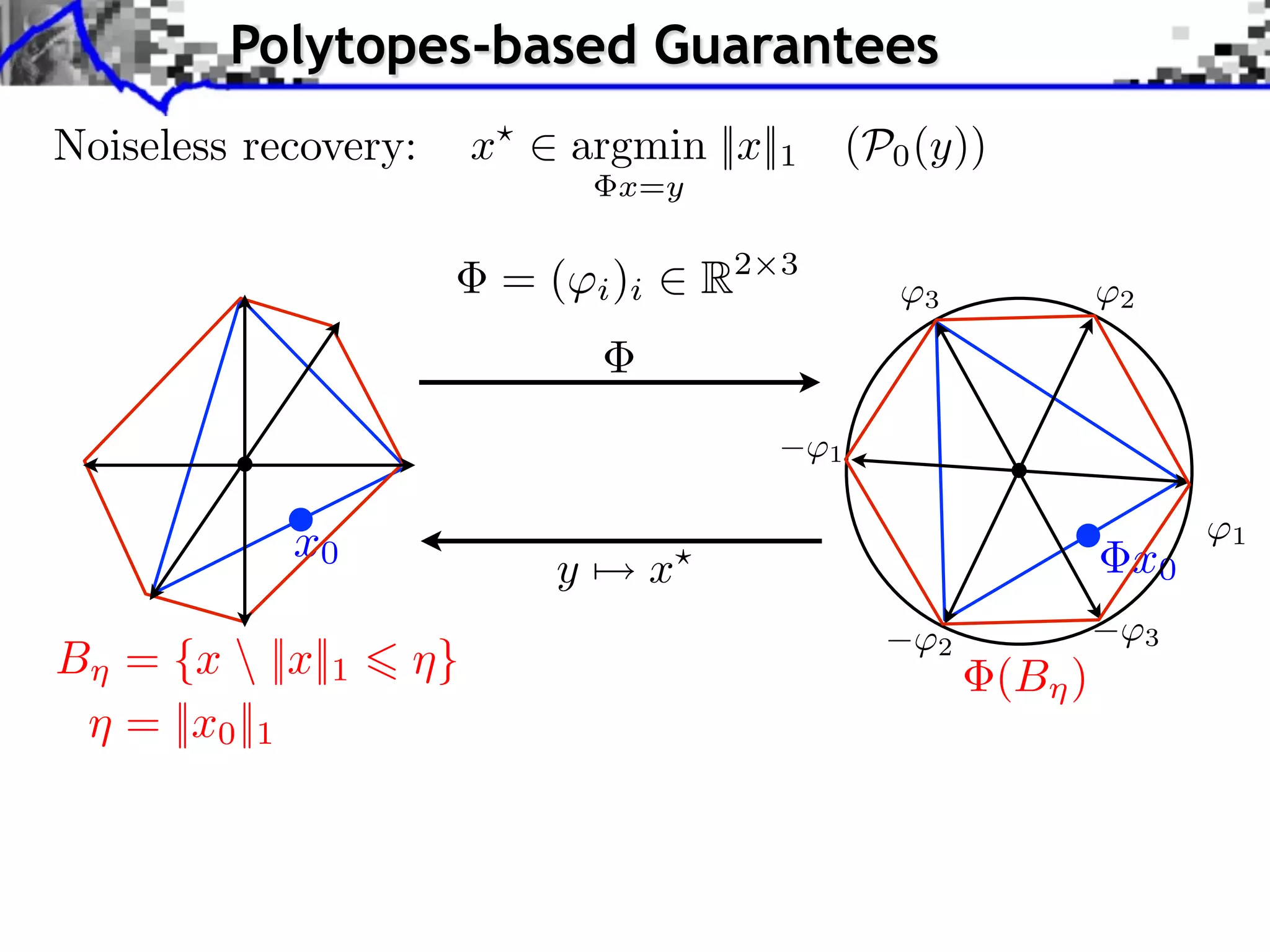
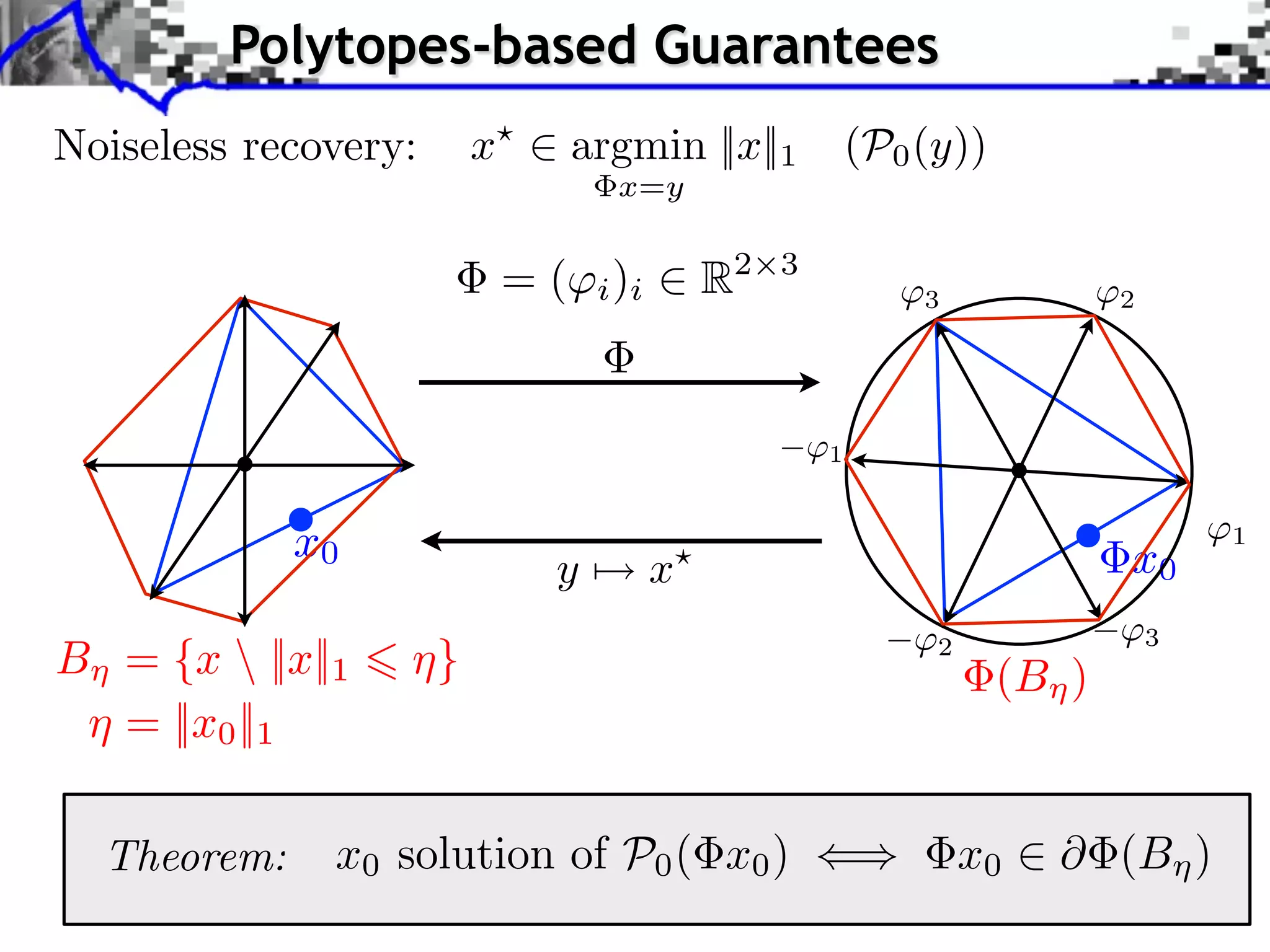
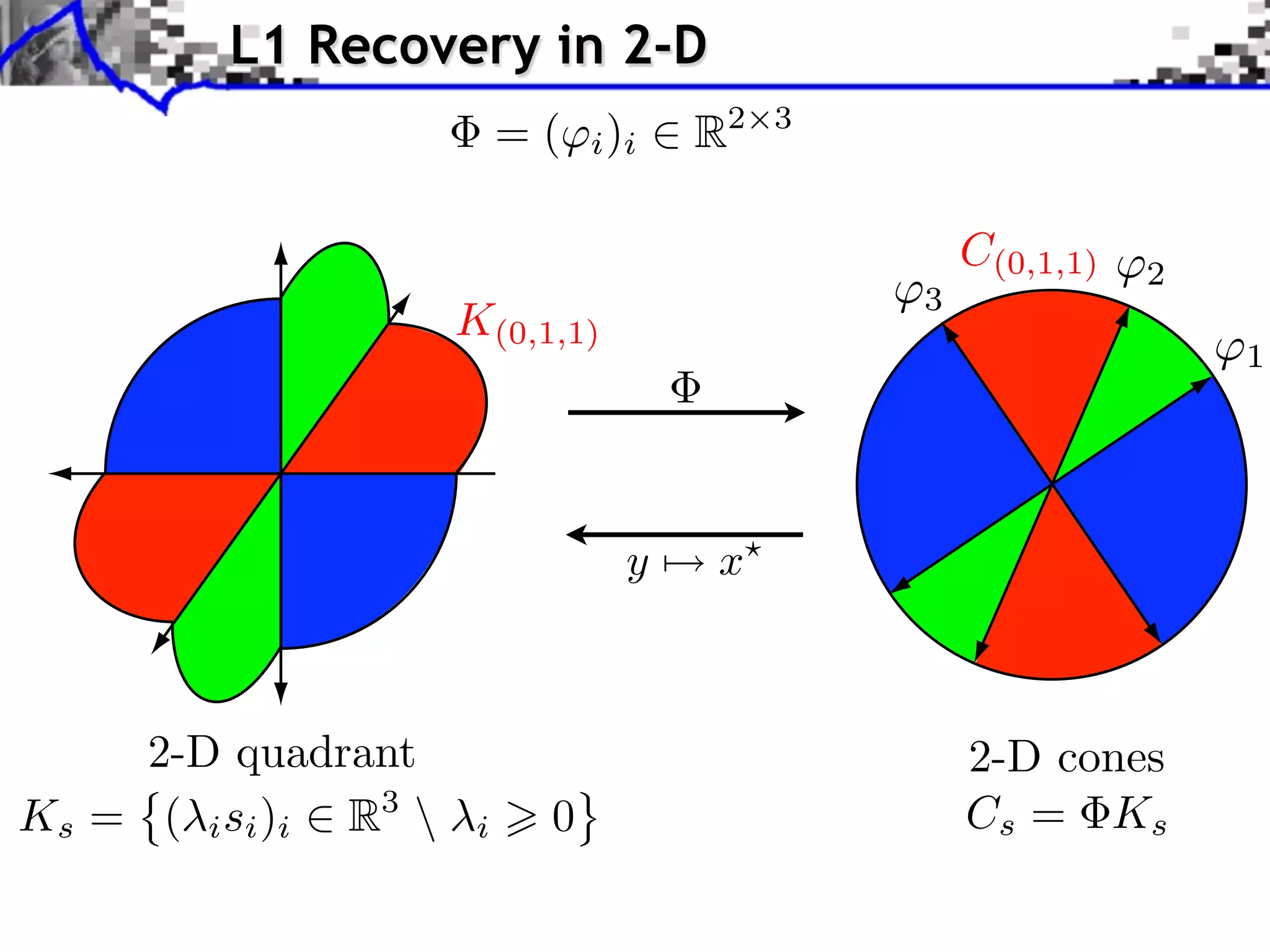
113. Polytope Noiseless Recovery
Counting faces of random polytopes: [Donoho]
All x0 such that ||x0 ||0 Call (P/N )P are identifiable.
Most x0 such that ||x0 ||0 Cmost (P/N )P are identifiable.
Call (1/4) 0.065
1
0.9
Cmost (1/4) 0.25 0.8
0.7
0.6
Sharp constants. 0.5
0.4
No noise robustness. 0.3
0.2
0.1
0
50 100 150 200 250 300 350 400
RIP
All Most

114. Polytope Noiseless Recovery
Counting faces of random polytopes: [Donoho]
All x0 such that ||x0 ||0 Call (P/N )P are identifiable.
Most x0 such that ||x0 ||0 Cmost (P/N )P are identifiable.
Call (1/4) 0.065
1
0.9
Cmost (1/4) 0.25 0.8
0.7
0.6
Sharp constants. 0.5
0.4
No noise robustness. 0.3
Computation of
0.2
0.1
“pathological” signals 0
50 100 150 200 250 300 350 400
[Dossal, P, Fadili, 2010]
RIP
All Most

115. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Theoritical Recovery Guarantees
• Compressed Sensing
• RIP and Polytopes CS Theory
• Fourier Measurements
• Convex Optimization via Proximal Splitting

116. Tomography and Fourier Measures

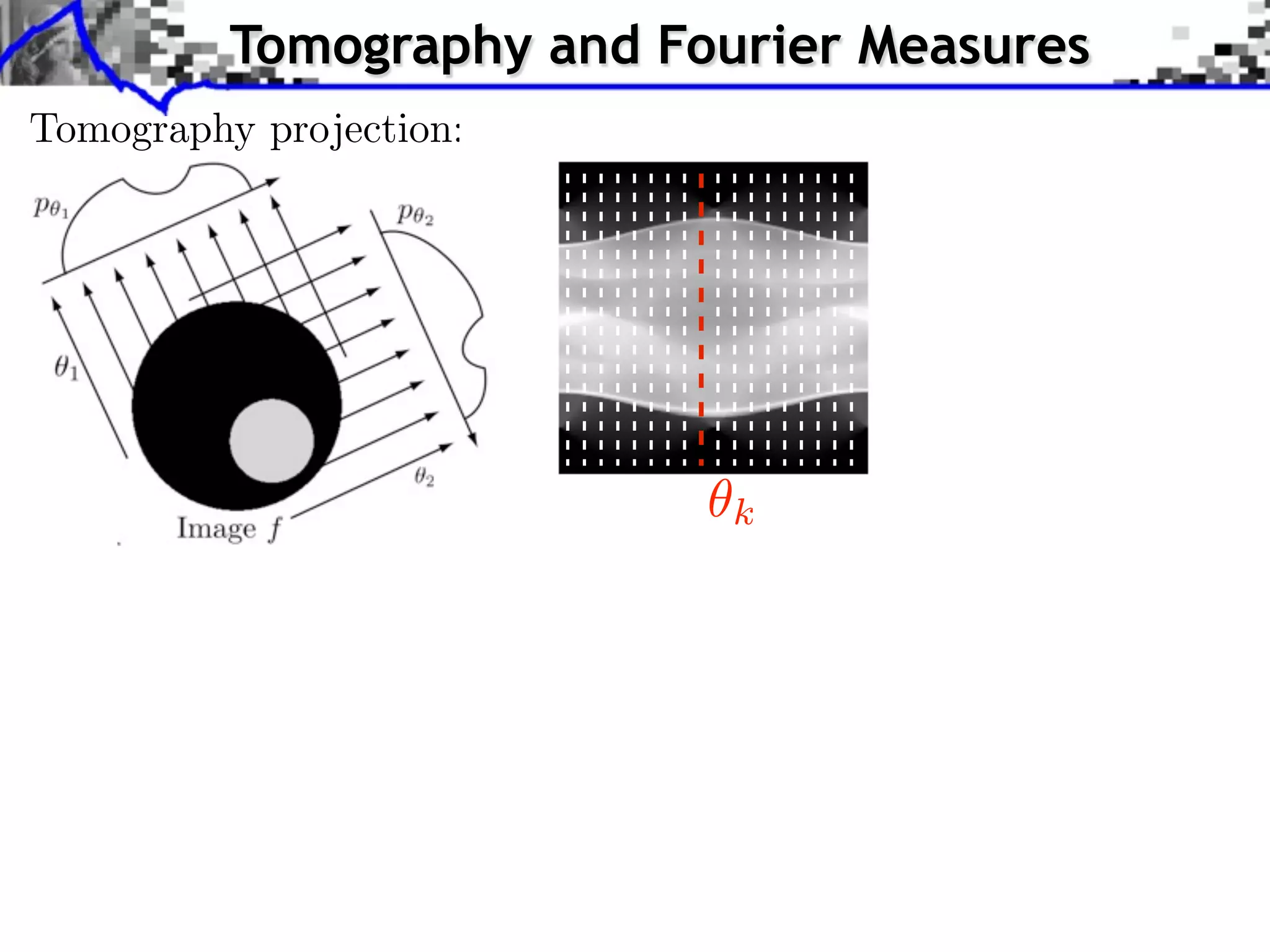
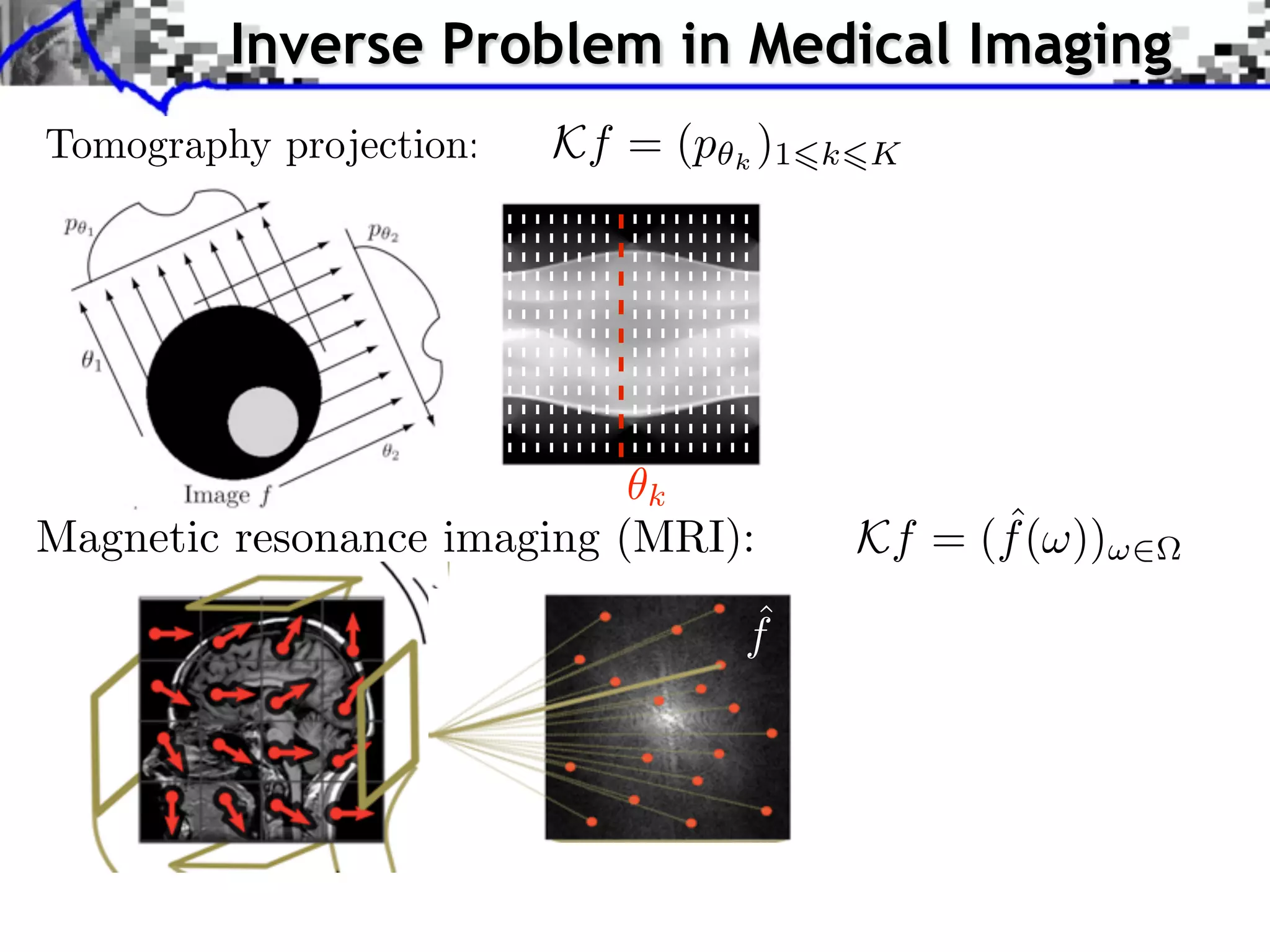
117. Tomography and Fourier Measures
ˆ
f = FFT2(f )
k
Fourier slice theorem: ˆ ˆ
p (⇥) = f (⇥ cos( ), ⇥ sin( ))
1D 2D Fourier
R
Partial Fourier measurements: {p k (t)}t
0 k<K
Equivalent to: ˆ
f = {f [ ]}

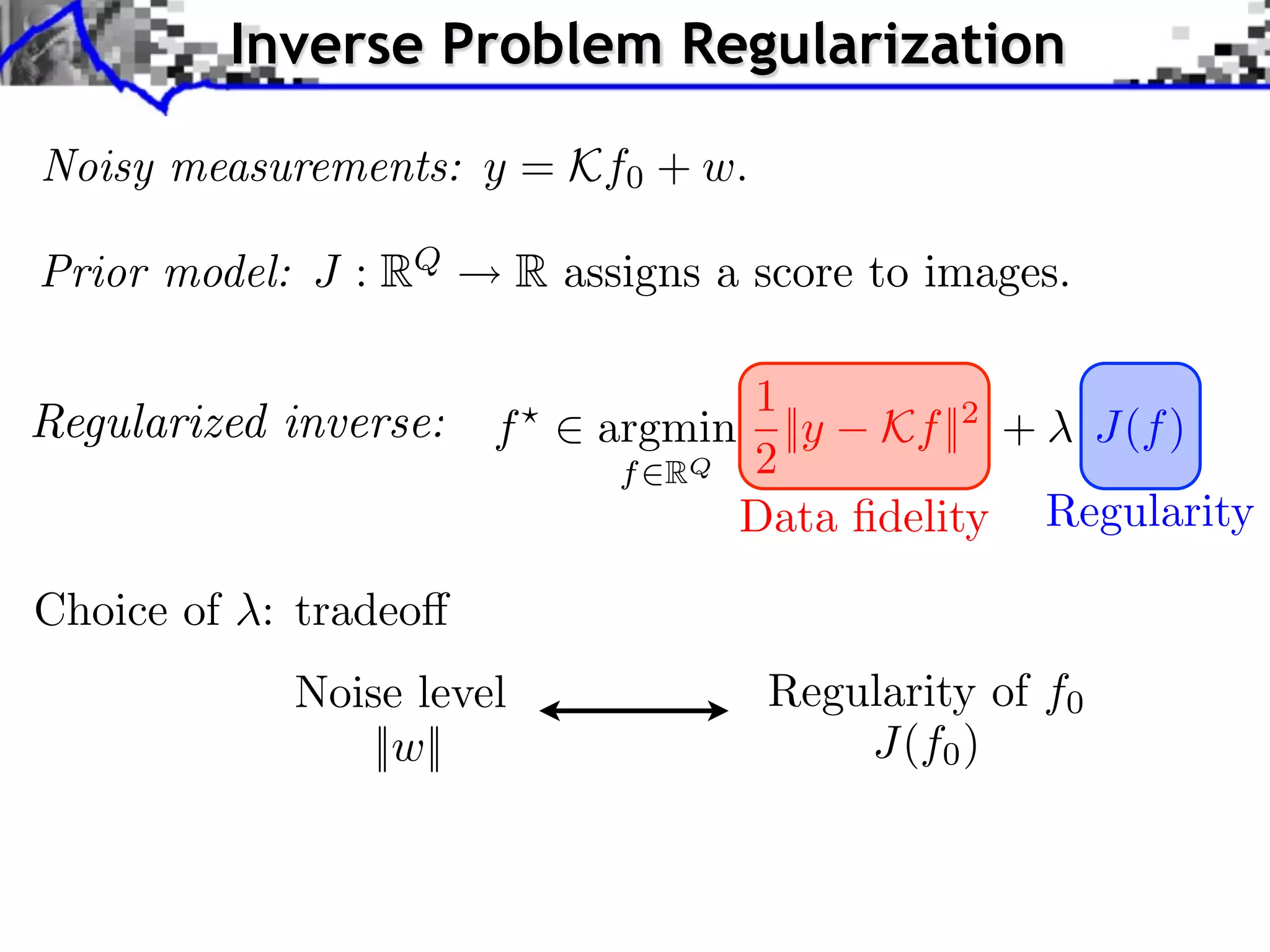
118. Regularized Inversion
Noisy measurements: ⇥ ˆ
, y[ ] = f0 [ ] + w[ ].
Noise: w[⇥] N (0, ), white noise.
1
regularization:
1 ˆ
f = argmin
⇥
|y[⇤] f [⇤]|2 + |⇥f, ⇥m ⇤|.
f 2 m
+ f
f
Disclaimer: this is not compressed sensing.

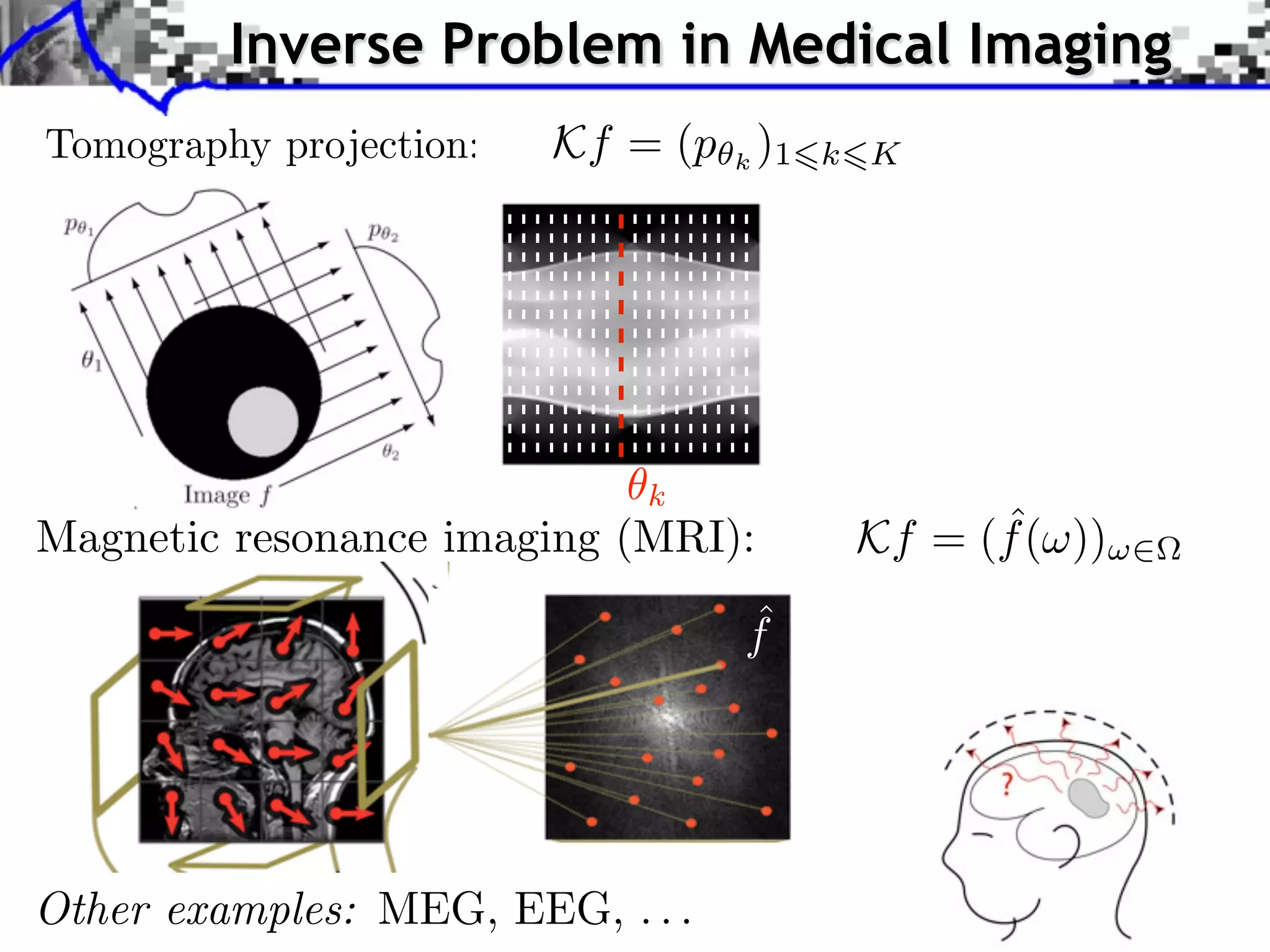
119. MRI Imaging
From [Lutsig et al.]

120. MRI Reconstruction
From [Lutsig et al.]
randomization
Fourier sub-sampling pattern:
High resolution Low resolution Linear Sparsity

121. Compressive Fourier Measurements
Sampling low frequencies helps.
Pseudo inverse Sparse wavelets

122. Structured Measurements
Gaussian matrices: intractable for large N .
Random partial orthogonal matrix: { } orthogonal basis.
=( ) where | | = P drawn uniformly at random.
Fast measurements: (e.g. Fourier basis)
, y[ ] = f, ⇥ ˆ
= f[ ]

123. Structured Measurements
Gaussian matrices: intractable for large N .
Random partial orthogonal matrix: { } orthogonal basis.
=( ) where | | = P drawn uniformly at random.
Fast measurements: (e.g. Fourier basis)
, ˆ
y[ ] = f, ⇥ = f [ ]
⌅ ⌅
Mutual incoherence: µ = N max |⇥⇥ , m ⇤| [1, N ]
,m

124. Structured Measurements
Gaussian matrices: intractable for large N .
Random partial orthogonal matrix: { } orthogonal basis.
=( ) where | | = P drawn uniformly at random.
Fast measurements: (e.g. Fourier basis)
, ˆ
y[ ] = f, ⇥ = f [ ]
⌅ ⌅
Mutual incoherence: µ = N max |⇥⇥ , m ⇤| [1, N ]
,m
Theorem: with high probability on ,
CP
If M 2 log(N )4
, then 2M 2 1
µ
[Rudelson, Vershynin, 2006]
not universal: requires incoherence.

125. Overview
• Inverse Problems Regularization
• Sparse Synthesis Regularization
• Theoritical Recovery Guarantees
• Compressed Sensing
• RIP and Polytopes CS Theory
• Fourier Measurements
• Convex Optimization via Proximal Splitting

126. Convex Optimization
Setting: G : H R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
Problem: min G(x)
x H

127. Convex Optimization
Setting: G : H R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
Problem: min G(x)
x H
Class of functions: x y
Convex: G(tx + (1 t)y) tG(x) + (1 t)G(y) t [0, 1]

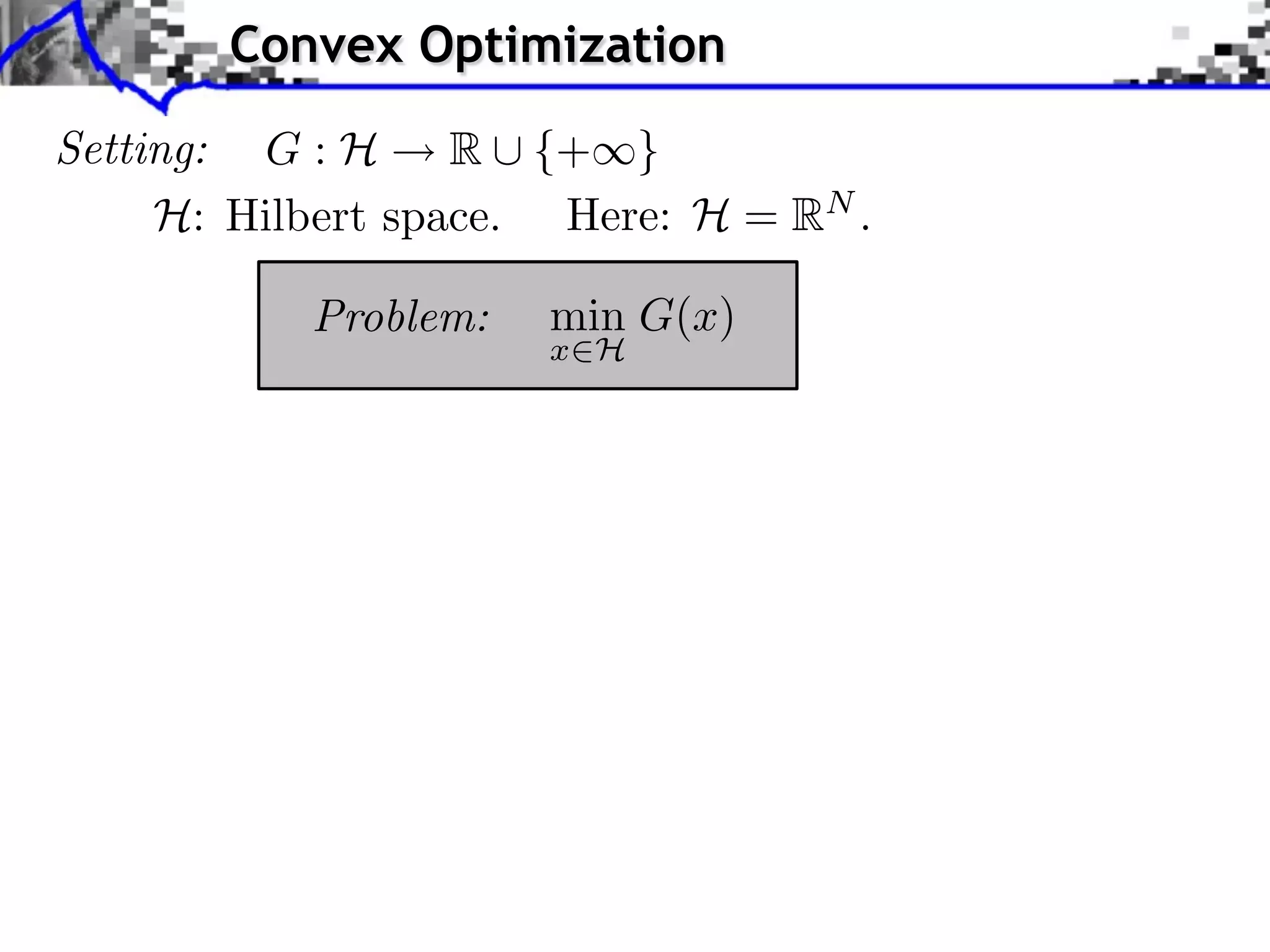
128. Convex Optimization
Setting: G : H R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
Problem: min G(x)
x H
Class of functions: x y
Convex: G(tx + (1 t)y) tG(x) + (1 t)G(y) t [0, 1]
Lower semi-continuous: lim inf G(x) G(x0 )
x x0
Proper: {x ⇥ H G(x) ⇤= + } = ⌅
⇤

129. Convex Optimization
Setting: G : H R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
Problem: min G(x)
x H
Class of functions: x y
Convex: G(tx + (1 t)y) tG(x) + (1 t)G(y) t [0, 1]
Lower semi-continuous: lim inf G(x) G(x0 )
x x0
Proper: {x ⇥ H G(x) ⇤= + } = ⌅
⇤
0 if x ⇥ C,
Indicator: C (x) =
+ otherwise.
(C closed and convex)

130. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x z||2 + G(z)
z 2

131. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x z||2 + G(z)
z 2
12 log(1 + x2 )
G(x) = ||x||1 = |xi | 10
|x| ||x||0
8
i 6
4
2
0
G(x) = ||x||0 = | {i xi = 0} | −2
G(x)
−10 −8 −6 −4 −2 0 2 4 6 8 10
G(x) = log(1 + |xi |2 )
i

132. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x z||2 + G(z)
z 2
12 log(1 + x2 )
G(x) = ||x||1 = |xi | 10
|x| ||x||0
8
i
Prox G (x)i = max 0, 1
6
xi 4
|xi | 2
0
G(x) = ||x||0 = | {i xi = 0} | −2
G(x)
−10 −8 −6 −4 −2 0 2 4 6 8 10
xi if |xi | 2 ,
10
Prox G (x)i =
8
0 otherwise.
6
4
2
0
G(x) = log(1 + |xi |2 ) −2
−4
i −6
3rd order polynomial root.
−8
ProxG (x)
−10
−10 −8 −6 −4 −2 0 2 4 6 8 10

133. Proximal Calculus
Separability: G(x) = G1 (x1 ) + . . . + Gn (xn )
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))

134. Proximal Calculus
Separability: G(x) = G1 (x1 ) + . . . + Gn (xn )
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))
1
Quadratic functionals: G(x) = || x y||2
2
Prox G = (Id + ) 1
= (Id + ) 1

135. Proximal Calculus
Separability: G(x) = G1 (x1 ) + . . . + Gn (xn )
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))
1
Quadratic functionals: G(x) = || x y||2
2
Prox G = (Id + ) 1
= (Id + ) 1
Composition by tight frame: A A = Id
ProxG A (x) =A ProxG A + Id A A

136. Proximal Calculus
Separability: G(x) = G1 (x1 ) + . . . + Gn (xn )
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))
1
Quadratic functionals: G(x) = || x y||2
2
Prox G = (Id + ) 1
= (Id + ) 1
Composition by tight frame: A A = Id
ProxG A (x) =A ProxG A + Id A A
x
Indicators: G(x) = C (x)
C
Prox G (x) = ProjC (x) ProjC (x)
= argmin ||x z||
z C

137. Gradient and Proximal Descents
Gradient descent: x( +1) = x( ) G(x( ) ) [explicit]
G is C 1 and G is L-Lipschitz
Theorem: If 0 < < 2/L, x( )
x a solution.

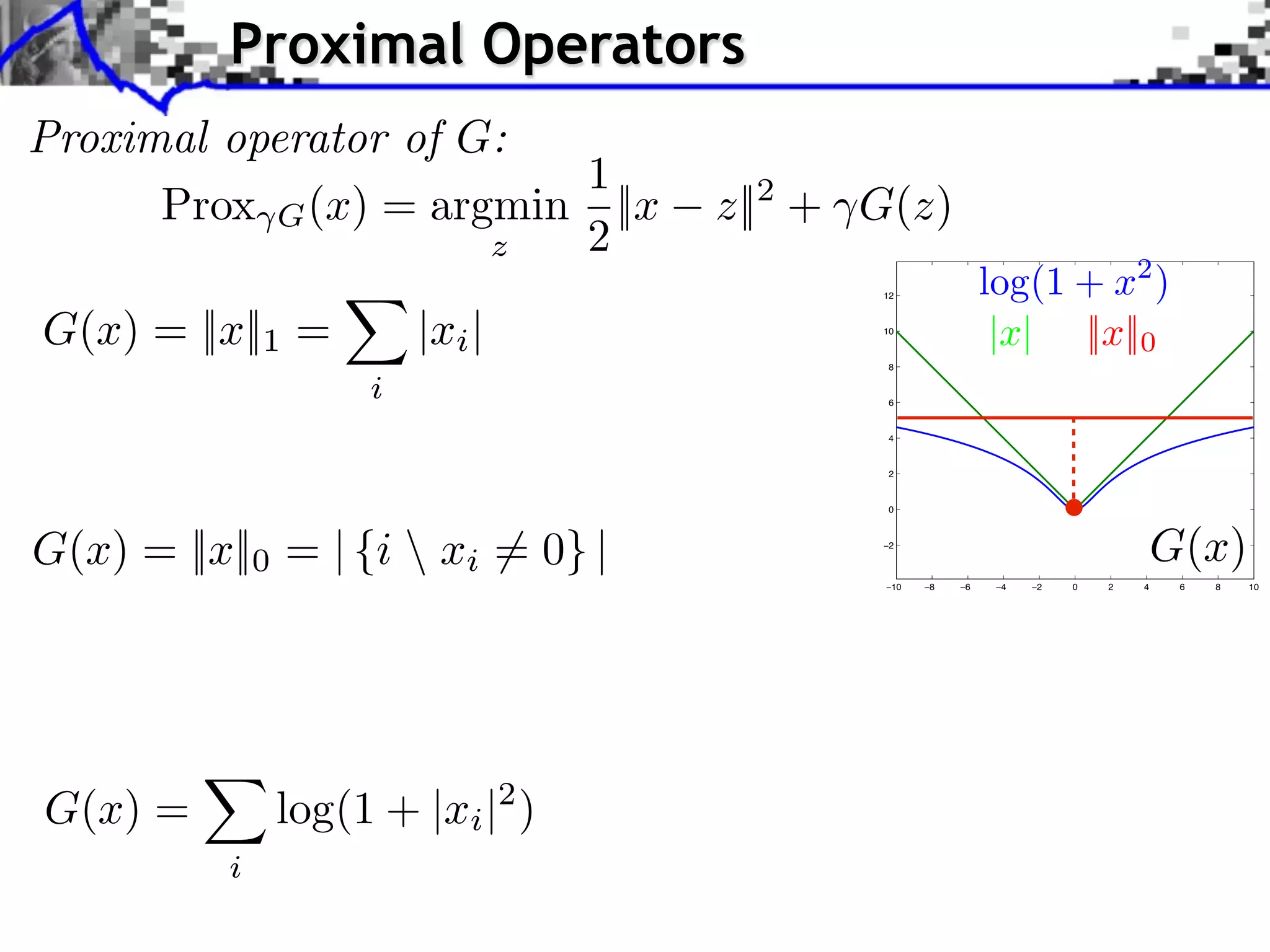
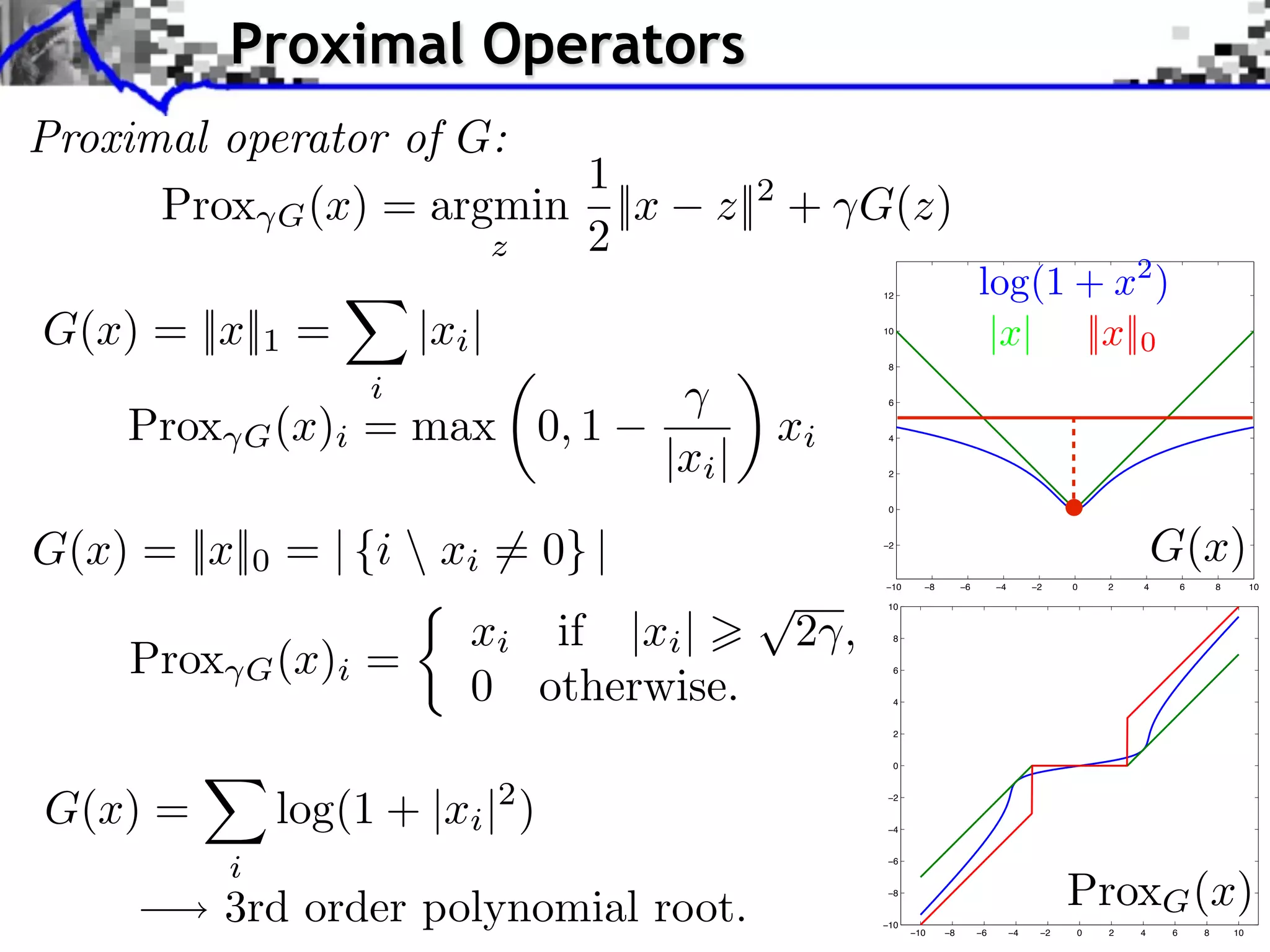
138. Gradient and Proximal Descents
Gradient descent: x( +1) = x( ) G(x( ) ) [explicit]
G is C 1 and G is L-Lipschitz
Theorem: If 0 < < 2/L, x( )
x a solution.
Sub-gradient descent: x( +1)
= x( )
v( ) , v( )
G(x( ) )
Theorem: If 1/⇥, x( )
x a solution.
Problem: slow.

139. Gradient and Proximal Descents
Gradient descent: x( +1) = x( ) G(x( ) ) [explicit]
G is C 1 and G is L-Lipschitz
Theorem: If 0 < < 2/L, x( )
x a solution.
Sub-gradient descent: x( +1)
= x( )
v( ) , v( )
G(x( ) )
Theorem: If 1/⇥, x( )
x a solution.
Problem: slow.
Proximal-point algorithm: x(⇥+1) = Prox G (x(⇥) ) [implicit]
Theorem: If c > 0, x( )
x a solution.
Prox G hard to compute.

140. Proximal Splitting Methods
Solve min E(x)
x H
Problem: Prox E is not available.

141. Proximal Splitting Methods
Solve min E(x)
x H
Problem: Prox E is not available.
Splitting: E(x) = F (x) + Gi (x)
i
Smooth Simple

142. Proximal Splitting Methods
Solve min E(x)
x H
Problem: Prox E is not available.
Splitting: E(x) = F (x) + Gi (x)
i
Smooth Simple
F (x)
Iterative algorithms using:
Prox Gi (x)
solves
Forward-Backward: F + G
Douglas-Rachford: Gi
Primal-Dual: Gi A
Generalized FB: F+ Gi

143. Smooth + Simple Splitting
Inverse problem: measurements y = Kf0 + w
f0 Kf0
K K : RN RP , P N
Model: f0 = x0 sparse in dictionary .
Sparse recovery: f = x where x solves
min F (x) + G(x)
x RN
Smooth Simple
1
Data fidelity: F (x) = ||y x||2 =K ⇥
2
Regularization: G(x) = ||x||1 = |xi |
i

144. Forward-Backward
Fix point equation:
x argmin F (x) + G(x) 0 F (x ) + G(x )
x
(x F (x )) x + ⇥G(x )
x⇥ = Prox G (x⇥ F (x⇥ ))

145. Forward-Backward
Fix point equation:
x argmin F (x) + G(x) 0 F (x ) + G(x )
x
(x F (x )) x + ⇥G(x )
x⇥ = Prox G (x⇥ F (x⇥ ))
Forward-backward: x(⇥+1) = Prox G x(⇥) F (x(⇥) )

146. Forward-Backward
Fix point equation:
x argmin F (x) + G(x) 0 F (x ) + G(x )
x
(x F (x )) x + ⇥G(x )
x⇥ = Prox G (x⇥ F (x⇥ ))
Forward-backward: x(⇥+1) = Prox G x(⇥) F (x(⇥) )
Projected gradient descent: G= C

147. Forward-Backward
Fix point equation:
x argmin F (x) + G(x) 0 F (x ) + G(x )
x
(x F (x )) x + ⇥G(x )
x⇥ = Prox G (x⇥ F (x⇥ ))
Forward-backward: x(⇥+1) = Prox G x(⇥) F (x(⇥) )
Projected gradient descent: G= C
Theorem: Let F be L-Lipschitz.
If < 2/L, x( )
x a solution of ( )

148. Example: L1 Regularization
1
min || x y||2 + ||x||1 min F (x) + G(x)
x 2 x
1
F (x) = || x y||2
2
F (x) = ( x y) L = || ||
G(x) = ||x||1
⇥
Prox G (x)i = max 0, 1 xi
|xi |
Forward-backward Iterative soft thresholding

149. Douglas Rachford Scheme
min G1 (x) + G2 (x) ( )
x
Simple Simple
Douglas-Rachford iterations:
z (⇥+1) = 1 z (⇥) + RProx G2 RProx G1 (z (⇥) )
2 2
x(⇥+1) = Prox G2 (z (⇥+1) )
Reflexive prox:
RProx G (x) = 2Prox G (x) x

150. Douglas Rachford Scheme
min G1 (x) + G2 (x) ( )
x
Simple Simple
Douglas-Rachford iterations:
z (⇥+1) = 1 z (⇥) + RProx G2 RProx G1 (z (⇥) )
2 2
x(⇥+1) = Prox G2 (z (⇥+1) )
Reflexive prox:
RProx G (x) = 2Prox G (x) x
Theorem: If 0 < < 2 and ⇥ > 0,
x( )
x a solution of ( )

151. Example: Constrainted L1
min ||x||1 min G1 (x) + G2 (x)
x=y x
G1 (x) = iC (x), C = {x x = y}
Prox G1 (x) = ProjC (x) = x +
⇥
( ⇥
) 1
(y x)
G2 (x) = ||x||1 Prox G2 (x) = max 0, 1 xi
|xi | i
e⇥cient if easy to invert.

152. Example: Constrainted L1
min ||x||1 min G1 (x) + G2 (x)
x=y x
G1 (x) = iC (x), C = {x x = y}
Prox G1 (x) = ProjC (x) = x +
⇥
( ⇥
) 1
(y x)
G2 (x) = ||x||1 Prox G2 (x) = max 0, 1 xi
|xi | i
e⇥cient if easy to invert. log10 (||x( ) ||1 ||x ||1 )
1
Example: compressed sensing −1
0
R100 400
Gaussian matrix −2
−3 = 0.01
y = x0 ||x0 ||0 = 17 −4 =1
−5
= 10
50 100 150 200 250

153. More than 2 Functionals
min G1 (x) + . . . + Gk (x) each Fi is simple
x
min G(x1 , . . . , xk ) + C (x1 , . . . , xk )
x
G(x1 , . . . , xk ) = G1 (x1 ) + . . . + Gk (xk )
C = (x1 , . . . , xk ) Hk x1 = . . . = xk

154. More than 2 Functionals
min G1 (x) + . . . + Gk (x) each Fi is simple
x
min G(x1 , . . . , xk ) + C (x1 , . . . , xk )
x
G(x1 , . . . , xk ) = G1 (x1 ) + . . . + Gk (xk )
C = (x1 , . . . , xk ) Hk x1 = . . . = xk
G and C are simple:
Prox G (x1 , . . . , xk ) = (Prox Gi (xi ))i
1
Prox ⇥C (x1 , . . . , xk ) = (˜, . . . , x)
x ˜ where x =
˜ xi
k i

155. Auxiliary Variables
min G1 (x) + G2 A(x) Linear map A : E H.
x
min G(z) + C (z) G1 , G2 simple.
z⇥H E
G(x, y) = G1 (x) + G2 (y)
C = {(x, y) ⇥ H E Ax = y}

156. Auxiliary Variables
min G1 (x) + G2 A(x) Linear map A : E H.
x
min G(z) + C (z) G1 , G2 simple.
z⇥H E
G(x, y) = G1 (x) + G2 (y)
C = {(x, y) ⇥ H E Ax = y}
Prox G (x, y) = (Prox G1 (x), Prox G2 (y))
Prox C (x, y) = (x + A y , y
˜ y ) = (˜, A˜)
˜ x x
y = (Id + AA )
˜ 1
(Ax y)
where
x = (Id + A A)
˜ 1
(A y + x)
e cient if Id + AA or Id + A A easy to invert.

157. Example: TV Regularization
1 ||u||1 = ||ui ||
min ||Kf y||2 + ||⇥f ||1
f 2 i
min G1 (f ) + G2 (f )
x
G1 (u) = ||u||1 Prox G1 (u)i = max 0, 1 ui
||ui ||
1
G2 (f ) = ||Kf y||2 Prox = (Id + K K) 1
K
2 G2
C = (f, u) ⇥ RN RN 2
u = ⇤f
˜ ˜
Prox C (f, u) = (f , f )

158. Example: TV Regularization
1 ||u||1 = ||ui ||
min ||Kf y||2 + ||⇥f ||1
f 2 i
min G1 (f ) + G2 (f )
x
G1 (u) = ||u||1 Prox G1 (u)i = max 0, 1 ui
||ui ||
1
G2 (f ) = ||Kf y||2 Prox = (Id + K K) 1
K
2 G2
C = (f, u) ⇥ RN RN 2
u = ⇤f
˜ ˜
Prox C (f, u) = (f , f )
Compute the solution of: (Id + ˜
)f = div(u) + f
O(N log(N )) operations using FFT.

159. Example: TV Regularization
Orignal f0 y = f0 + w Recovery f
y = Kx0 Iteration

160. Conclusion
Sparsity: approximate signals with few atoms.
dictionary

161. Conclusion
Sparsity: approximate signals with few atoms.
dictionary
Compressed sensing ideas:
Randomized sensors + sparse recovery.
Number of measurements signal complexity.
CS is about designing new hardware.

162. Conclusion
Sparsity: approximate signals with few atoms.
dictionary
Compressed sensing ideas:
Randomized sensors + sparse recovery.
Number of measurements signal complexity.
CS is about designing new hardware.
The devil is in the constants:
Worse case analysis is problematic.
Designing good signal models.

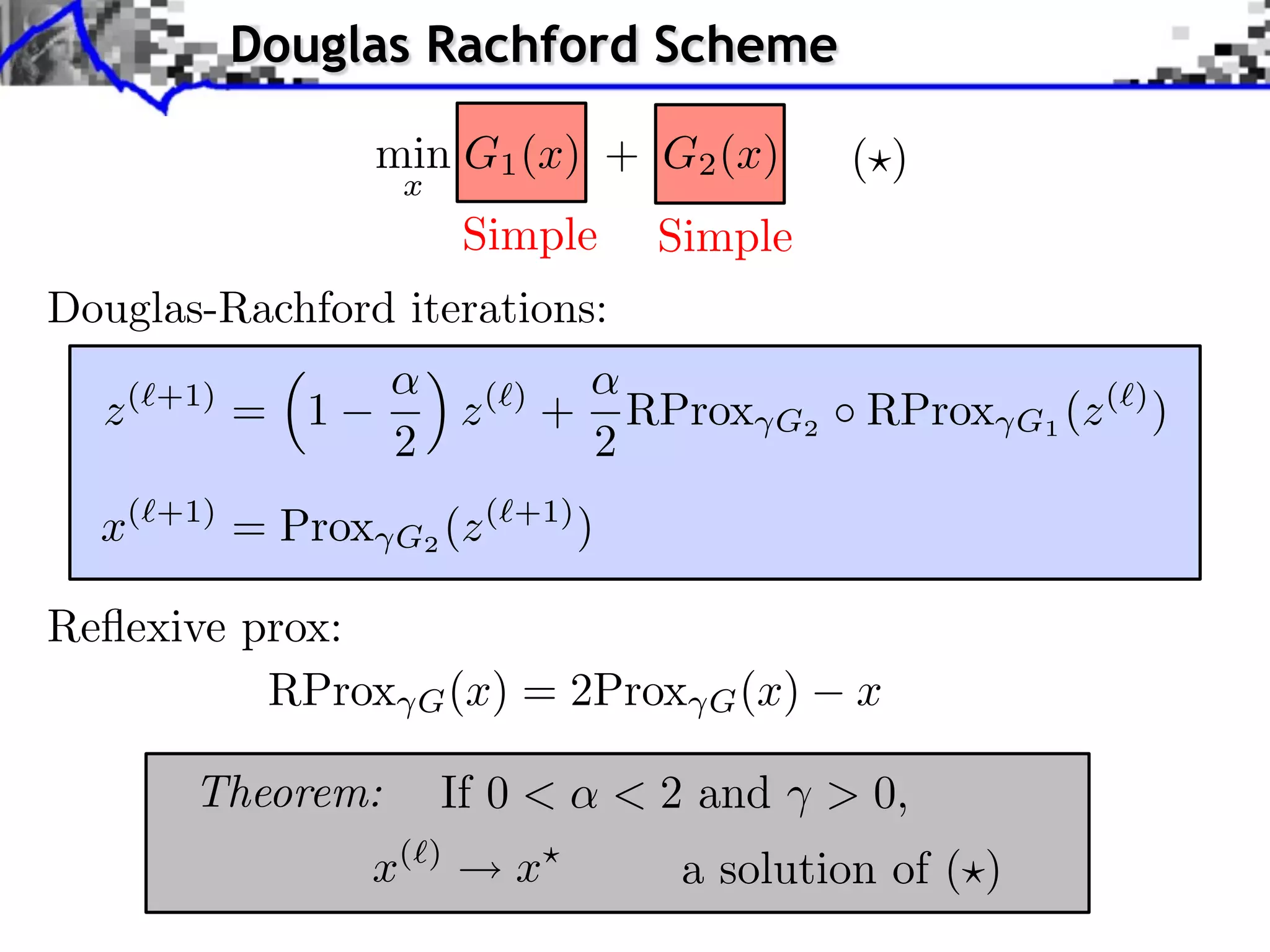
163. RAINED DICTIONARY. THE BOTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 IT
CALE K-SVD ALGORITHM [2] ON EACH CHANNEL SEPARATELY WITH 8
EPRESENTATION FOR COLOR IMAGE RESTORATION
DENOISING ALGORITHM WITH 256 ATOMS OF SIZE 7 7 3 FOR
ESULTS ARE THOSE GIVEN BY MCAULEY AND AL [28] WITH THEIR “3 Some Hot Topics
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
uced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
h is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
Dictionary learning:
dB.
with 256 atoms learned on a generic database of natural images, with two different sizes ofREPRESENTATION FOR COLOR IMAGE RESTORATION
MAIRAL et al.: SPARSE patches. Note the large number of color-less atoms. 57
ave negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5 5 3 patches; (b) 8 8 3 patches.
R IMAGE RESTORATION 61
Fig. 7. Data set used for evaluating denoising experiments.
learning
ing Image; (b) resulting dictionary; (b) is the dictionary learned in the image in (a). The dictionary is more colored than the global one.
TABLE I
g. 7. Data set used for evaluating denoising experiments. with 256 atoms learned on a generic database of natural images, with two different sizes of patches. Note the large number of color-less atoms.
Fig. 2. Dictionaries
Since the atoms can have negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5 5 3 patches; (b) 8 8 3 patches.
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
duced with our proposed technique (
TABLE I our proposed new metric). Both images have been denoised with the same global dictionary.
in
TH 256 ATOMS OF SIZE castle 7 in3 FOR of the water. What is more, the color of the sky is.piecewise CASE IS DIVIDED IN FOUR
a bias effect in the color from the 7 and some part AND 6 6 3 FOR EACH constant when
ch is another artifact our approach corrected. (a)HEIR “3(b) Original algorithm, HE TOP-RIGHT RESULTS ARE THOSE OBTAINED BY
Y MCAULEY AND AL [28] WITH T Original. 3 MODEL.” T dB. (c) Proposed algorithm,
3 MODEL.” THE TOP-RIGHT RESULTS ARE THOSE O
dB.
8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS
2] ON EACH CHANNEL SEPARATELY WITH 8 8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS OBTAINED
AND 6
OTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 ITERATIONS.
H GROUP. AS CAN BE SEEN, OUR PROPOSED TECHNIQUE CONSISTENTLY PRODUCES THE BEST RESULTS
6 3 FOR
Fig. 3. Examples of color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
Color artifacts are reduced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
In (b), one observes a bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
(false contours), which is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
. EACH CASE IS DIVID

164. RAINED DICTIONARY. THE BOTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 IT
CALE K-SVD ALGORITHM [2] ON EACH CHANNEL SEPARATELY WITH 8
EPRESENTATION FOR COLOR IMAGE RESTORATION
DENOISING ALGORITHM WITH 256 ATOMS OF SIZE 7 7 3 FOR
ESULTS ARE THOSE GIVEN BY MCAULEY AND AL [28] WITH THEIR “3 Some Hot Topics
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
uced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
Image f =
h is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
Dictionary learning:
with 256 atoms learned on a generic database of natural images, with two different sizes ofREPRESENTATION FOR COLOR IMAGE RESTORATION
ave negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5
MAIRAL et al.: SPARSE patches. Note the large number of color-less
5 3 patches; (b) 8 8
atoms.
3 patches.
57
x
R IMAGE RESTORATION 61
Fig. 7. Data set used for evaluating denoising experiments.
learning
ing Image; (b) resulting dictionary; (b) is the dictionary learned in the image in (a). The dictionary is more colored than the global one.
TABLE I
Analysis vs. synthesis:
g. 7. Data set used for evaluating denoising experiments. with 256 atoms learned on a generic database of natural images, with two different sizes of patches. Note the large number of color-less atoms.
Fig. 2. Dictionaries
Since the atoms can have negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5 5 3 patches; (b) 8 8 3 patches.
Js (f ) = min ||x||1
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed (
TABLE I in the new metric).
duced with our proposed technique (
a bias effect in the color from the 7
in our proposed new metric). Both images have been denoised with the same global dictionary.
TH 256 ATOMS OF SIZE castle 7 in3 FOR of the water. What is more, the color of the sky is.piecewise CASE IS DIVIDED IN FOUR
and some part AND 6 6 3 FOR EACH constant when
f= x
ch is another artifact our approach corrected. (a)HEIR “3(b) Original algorithm, HE TOP-RIGHT RESULTS ARE THOSE OBTAINED BY
Y MCAULEY AND AL [28] WITH T Original. 3 MODEL.” T dB. (c) Proposed algorithm,
3 MODEL.” THE TOP-RIGHT RESULTS ARE THOSE O
dB.
8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS
2] ON EACH CHANNEL SEPARATELY WITH 8 8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS OBTAINED
AND 6
OTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 ITERATIONS.
H GROUP. AS CAN BE SEEN, OUR PROPOSED TECHNIQUE CONSISTENTLY PRODUCES THE BEST RESULTS
Coe cients x
6 3 FOR
Fig. 3. Examples of color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
Color artifacts are reduced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
In (b), one observes a bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
(false contours), which is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
. EACH CASE IS DIVID

165. RAINED DICTIONARY. THE BOTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 IT
CALE K-SVD ALGORITHM [2] ON EACH CHANNEL SEPARATELY WITH 8
EPRESENTATION FOR COLOR IMAGE RESTORATION
DENOISING ALGORITHM WITH 256 ATOMS OF SIZE 7 7 3 FOR
ESULTS ARE THOSE GIVEN BY MCAULEY AND AL [28] WITH THEIR “3 Some Hot Topics
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
uced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
Image f =
h is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
Dictionary learning:
with 256 atoms learned on a generic database of natural images, with two different sizes ofREPRESENTATION FOR COLOR IMAGE RESTORATION
ave negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5
MAIRAL et al.: SPARSE patches. Note the large number of color-less
5 3 patches; (b) 8 8
atoms.
3 patches.
57
x
R IMAGE RESTORATION 61
Fig. 7. Data set used for evaluating denoising experiments.
learning
D
ing Image; (b) resulting dictionary; (b) is the dictionary learned in the image in (a). The dictionary is more colored than the global one.
TABLE I
Analysis vs. synthesis:
g. 7. Data set used for evaluating denoising experiments. with 256 atoms learned on a generic database of natural images, with two different sizes of patches. Note the large number of color-less atoms.
Fig. 2. Dictionaries
Since the atoms can have negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5 5 3 patches; (b) 8 8 3 patches.
Js (f ) = min ||x||1
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed (
TABLE I in the new metric).
duced with our proposed technique (
a bias effect in the color from the 7
in our proposed new metric). Both images have been denoised with the same global dictionary.
TH 256 ATOMS OF SIZE castle 7 in3 FOR of the water. What is more, the color of the sky is.piecewise CASE IS DIVIDED IN FOUR
and some part AND 6 6 3 FOR EACH constant when
f= x
J (f ) = ||D f ||
ch is another artifact our approach corrected. (a)HEIR “3(b) Original algorithm, HE TOP-RIGHT RESULTS ARE THOSE OBTAINED BY
Y MCAULEY AND AL [28] WITH T Original. 3 MODEL.” T dB. (c) Proposed algorithm,
3 MODEL.” THE TOP-RIGHT RESULTS ARE THOSE O
dB.
8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS
a 1
2] ON EACH CHANNEL SEPARATELY WITH 8 8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS OBTAINED
AND 6
OTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 ITERATIONS.
H GROUP. AS CAN BE SEEN, OUR PROPOSED TECHNIQUE CONSISTENTLY PRODUCES THE BEST RESULTS
Coe cients x c=D f
6 3 FOR
Fig. 3. Examples of color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
Color artifacts are reduced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
In (b), one observes a bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
(false contours), which is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
. EACH CASE IS DIVID

166. RAINED DICTIONARY. THE BOTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 IT
CALE K-SVD ALGORITHM [2] ON EACH CHANNEL SEPARATELY WITH 8
EPRESENTATION FOR COLOR IMAGE RESTORATION
DENOISING ALGORITHM WITH 256 ATOMS OF SIZE 7 7 3 FOR
ESULTS ARE THOSE GIVEN BY MCAULEY AND AL [28] WITH THEIR “3 Some Hot Topics
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
uced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
Image f =
h is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
Dictionary learning:
with 256 atoms learned on a generic database of natural images, with two different sizes ofREPRESENTATION FOR COLOR IMAGE RESTORATION
ave negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5
MAIRAL et al.: SPARSE patches. Note the large number of color-less
5 3 patches; (b) 8 8
atoms.
3 patches.
57
x
R IMAGE RESTORATION 61
Fig. 7. Data set used for evaluating denoising experiments.
learning
D
ing Image; (b) resulting dictionary; (b) is the dictionary learned in the image in (a). The dictionary is more colored than the global one.
TABLE I
Analysis vs. synthesis:
g. 7. Data set used for evaluating denoising experiments. with 256 atoms learned on a generic database of natural images, with two different sizes of patches. Note the large number of color-less atoms.
Fig. 2. Dictionaries
Since the atoms can have negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5 5 3 patches; (b) 8 8 3 patches.
Js (f ) = min ||x||1
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed (
TABLE I in the new metric).
duced with our proposed technique (
a bias effect in the color from the 7
in our proposed new metric). Both images have been denoised with the same global dictionary.
TH 256 ATOMS OF SIZE castle 7 in3 FOR of the water. What is more, the color of the sky is.piecewise CASE IS DIVIDED IN FOUR
and some part AND 6 6 3 FOR EACH constant when
f= x
J (f ) = ||D f ||
ch is another artifact our approach corrected. (a)HEIR “3(b) Original algorithm, HE TOP-RIGHT RESULTS ARE THOSE OBTAINED BY
Y MCAULEY AND AL [28] WITH T Original. 3 MODEL.” T dB. (c) Proposed algorithm,
3 MODEL.” THE TOP-RIGHT RESULTS ARE THOSE O
dB.
8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS
a 1
2] ON EACH CHANNEL SEPARATELY WITH 8 8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS OBTAINED
AND 6
OTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 ITERATIONS.
Other sparse priors:
H GROUP. AS CAN BE SEEN, OUR PROPOSED TECHNIQUE CONSISTENTLY PRODUCES THE BEST RESULTS
Coe cients x c=D f
6 3 FOR
Fig. 3. Examples of color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
Color artifacts are reduced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
In (b), one observes a bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
(false contours), which is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
. EACH CASE IS DIVID
|x1 | + |x2 | max(|x1 |, |x2 |)

167. RAINED DICTIONARY. THE BOTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 IT
CALE K-SVD ALGORITHM [2] ON EACH CHANNEL SEPARATELY WITH 8
EPRESENTATION FOR COLOR IMAGE RESTORATION
DENOISING ALGORITHM WITH 256 ATOMS OF SIZE 7 7 3 FOR
ESULTS ARE THOSE GIVEN BY MCAULEY AND AL [28] WITH THEIR “3 Some Hot Topics
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
uced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
Image f =
h is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
Dictionary learning:
with 256 atoms learned on a generic database of natural images, with two different sizes ofREPRESENTATION FOR COLOR IMAGE RESTORATION
ave negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5
MAIRAL et al.: SPARSE patches. Note the large number of color-less
5 3 patches; (b) 8 8
atoms.
3 patches.
57
x
R IMAGE RESTORATION 61
Fig. 7. Data set used for evaluating denoising experiments.
learning
D
ing Image; (b) resulting dictionary; (b) is the dictionary learned in the image in (a). The dictionary is more colored than the global one.
TABLE I
Analysis vs. synthesis:
g. 7. Data set used for evaluating denoising experiments. with 256 atoms learned on a generic database of natural images, with two different sizes of patches. Note the large number of color-less atoms.
Fig. 2. Dictionaries
Since the atoms can have negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5 5 3 patches; (b) 8 8 3 patches.
Js (f ) = min ||x||1
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed (
TABLE I in the new metric).
duced with our proposed technique (
a bias effect in the color from the 7
in our proposed new metric). Both images have been denoised with the same global dictionary.
TH 256 ATOMS OF SIZE castle 7 in3 FOR of the water. What is more, the color of the sky is.piecewise CASE IS DIVIDED IN FOUR
and some part AND 6 6 3 FOR EACH constant when
f= x
J (f ) = ||D f ||
ch is another artifact our approach corrected. (a)HEIR “3(b) Original algorithm, HE TOP-RIGHT RESULTS ARE THOSE OBTAINED BY
Y MCAULEY AND AL [28] WITH T Original. 3 MODEL.” T dB. (c) Proposed algorithm,
3 MODEL.” THE TOP-RIGHT RESULTS ARE THOSE O
dB.
8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS
a 1
2] ON EACH CHANNEL SEPARATELY WITH 8 8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS OBTAINED
AND 6
OTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 ITERATIONS.
Other sparse priors:
H GROUP. AS CAN BE SEEN, OUR PROPOSED TECHNIQUE CONSISTENTLY PRODUCES THE BEST RESULTS
Coe cients x c=D f
6 3 FOR
Fig. 3. Examples of color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
Color artifacts are reduced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
In (b), one observes a bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
(false contours), which is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
. EACH CASE IS DIVID
2 1
|x1 | + |x2 | max(|x1 |, |x2 |) |x1 | + (x2
2 + x3 ) 2

168. RAINED DICTIONARY. THE BOTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 IT
CALE K-SVD ALGORITHM [2] ON EACH CHANNEL SEPARATELY WITH 8
EPRESENTATION FOR COLOR IMAGE RESTORATION
DENOISING ALGORITHM WITH 256 ATOMS OF SIZE 7 7 3 FOR
ESULTS ARE THOSE GIVEN BY MCAULEY AND AL [28] WITH THEIR “3 Some Hot Topics
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
uced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
Image f =
h is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
Dictionary learning:
with 256 atoms learned on a generic database of natural images, with two different sizes ofREPRESENTATION FOR COLOR IMAGE RESTORATION
ave negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5
MAIRAL et al.: SPARSE patches. Note the large number of color-less
5 3 patches; (b) 8 8
atoms.
3 patches.
57
x
R IMAGE RESTORATION 61
Fig. 7. Data set used for evaluating denoising experiments.
learning
D
ing Image; (b) resulting dictionary; (b) is the dictionary learned in the image in (a). The dictionary is more colored than the global one.
TABLE I
Analysis vs. synthesis:
g. 7. Data set used for evaluating denoising experiments. with 256 atoms learned on a generic database of natural images, with two different sizes of patches. Note the large number of color-less atoms.
Fig. 2. Dictionaries
Since the atoms can have negative values, the vectors are presented scaled and shifted to the [0,255] range per channel: (a) 5 5 3 patches; (b) 8 8 3 patches.
Js (f ) = min ||x||1
color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed (
TABLE I in the new metric).
duced with our proposed technique (
a bias effect in the color from the 7
in our proposed new metric). Both images have been denoised with the same global dictionary.
TH 256 ATOMS OF SIZE castle 7 in3 FOR of the water. What is more, the color of the sky is.piecewise CASE IS DIVIDED IN FOUR
and some part AND 6 6 3 FOR EACH constant when
f= x
J (f ) = ||D f ||
ch is another artifact our approach corrected. (a)HEIR “3(b) Original algorithm, HE TOP-RIGHT RESULTS ARE THOSE OBTAINED BY
Y MCAULEY AND AL [28] WITH T Original. 3 MODEL.” T dB. (c) Proposed algorithm,
3 MODEL.” THE TOP-RIGHT RESULTS ARE THOSE O
dB.
8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS
a 1
2] ON EACH CHANNEL SEPARATELY WITH 8 8 ATOMS. THE BOTTOM-LEFT ARE OUR RESULTS OBTAINED
AND 6
OTTOM-RIGHT ARE THE IMPROVEMENTS OBTAINED WITH THE ADAPTIVE APPROACH WITH 20 ITERATIONS.
Other sparse priors:
H GROUP. AS CAN BE SEEN, OUR PROPOSED TECHNIQUE CONSISTENTLY PRODUCES THE BEST RESULTS
Coe cients x c=D f
6 3 FOR
Fig. 3. Examples of color artifacts while reconstructing a damaged version of the image (a) without the improvement here proposed ( in the new metric).
Color artifacts are reduced with our proposed technique ( in our proposed new metric). Both images have been denoised with the same global dictionary.
In (b), one observes a bias effect in the color from the castle and in some part of the water. What is more, the color of the sky is piecewise constant when
(false contours), which is another artifact our approach corrected. (a) Original. (b) Original algorithm, dB. (c) Proposed algorithm,
dB.
. EACH CASE IS DIVID
2 1
|x1 | + |x2 | max(|x1 |, |x2 |) |x1 | + (x2
2 + x3 ) 2 Nuclear