The document discusses proximal splitting methods for solving optimization problems involving the minimization of a sum of functions. It first introduces subdifferential calculus and proximal operators. It then describes several proximal splitting algorithms, including forward-backward splitting, Douglas-Rachford splitting, primal-dual splitting, and generalized forward-backward splitting. These algorithms allow solving composite optimization problems by exploiting the separable structure and properties like smoothness or proximity of the individual terms. The document provides examples of applying such methods to inverse problems like sparse recovery.

1. Low Complexity
Regularization of
Inverse Problems
Cours #3
Proximal Splitting Methods
Gabriel Peyré
www.numerical-tours.com

2. Overview of the Course
• Course #1: Inverse Problems
• Course #2: Recovery Guarantees
• Course #3: Proximal Splitting Methods

3. Convex Optimization
Setting: G : H
R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
Problem:
min G(x)
x H

4. Convex Optimization
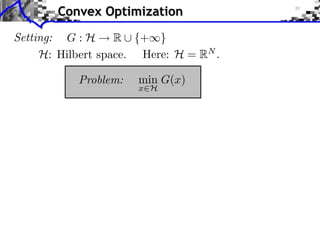
Setting: G : H
R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
Problem:
Class of functions:
Convex: G(tx + (1
min G(x)
x H
y
x
t)y)
tG(x) + (1
t)G(y)
t
[0, 1]

5. Convex Optimization
Setting: G : H
R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
Problem:
Class of functions:
Convex: G(tx + (1
min G(x)
x H
y
x
t)y)
Lower semi-continuous:
tG(x) + (1
t)G(y)
lim inf G(x)
G(x0 )
x
x0
Proper: {x ⇥ H G(x) ⇤= + } = ⌅
⇤
t
[0, 1]

6. Convex Optimization
Setting: G : H
R ⇤ {+⇥}
H: Hilbert space. Here: H = RN .
min G(x)
Problem:
Class of functions:
Convex: G(tx + (1
x H
t)y)
Lower semi-continuous:
tG(x) + (1
t)G(y)
lim inf G(x)
G(x0 )
x
x0
Proper: {x ⇥ H G(x) ⇤= + } = ⌅
⇤
Indicator:
y
x
C (x)
=
(C closed and convex)
0 if x ⇥ C,
+
otherwise.
t
[0, 1]

7. Example:
Inverse problem:
f0
K
1
Regularization
measurements
Kf0
y = Kf0 + w
K : RN
RP ,
P
N

8. Example:
Inverse problem:
f0
Model: f0 =
x RQ
coe cients
K
1
Regularization
measurements
Kf0
y = Kf0 + w
K : RN
x0 sparse in dictionary
f=
x R
image
N
= K ⇥ ⇥ RP
K
Q
RP ,
RN
Q
,Q
P
N
N.
y = Kf RP
observations

9. Example:
Inverse problem:
f0
Model: f0 =
x RQ
coe cients
K
1
Regularization
measurements
Kf0
y = Kf0 + w
K : RN
x0 sparse in dictionary
f=
x R
image
N
= K ⇥ ⇥ RP
K
Q
Sparse recovery: f = x where x solves
1
min
||y
x||2 + ||x||1
x RN 2
Fidelity Regularization
RP ,
RN
Q
,Q
P
N
N.
y = Kf RP
observations

10. Example:
1
Regularization
Inpainting: masking operator K
fi if i
,
(Kf )i =
0 otherwise.
K : RN
RN
Q
RP
c
P =| |
translation invariant wavelet frame.
Orignal f0 =
x0
y = x0 + w
Recovery
x

11. Overview
• Subdifferential Calculus
• Proximal Calculus
• Forward Backward
• Douglas Rachford
• Generalized Forward-Backward
• Duality

12. Sub-differential
Sub-di erential:
G(x) = {u ⇥ H ⇤ z, G(z)
G(x) + ⌅u, z
x⇧}
G(x) = |x|
G(0) = [ 1, 1]

13. Sub-differential
Sub-di erential:
G(x) = {u ⇥ H ⇤ z, G(z)
Smooth functions:
G(x) + ⌅u, z
x⇧}
G(x) = |x|
If F is C 1 , F (x) = { F (x)}
G(0) = [ 1, 1]

14. Sub-differential
Sub-di erential:
G(x) = {u ⇥ H ⇤ z, G(z)
G(x) + ⌅u, z
x⇧}
G(x) = |x|
Smooth functions:
If F is C 1 , F (x) = { F (x)}
G(0) = [ 1, 1]
First-order conditions:
x
argmin G(x)
x H
0
G(x )

15. Sub-differential
Sub-di erential:
G(x) = {u ⇥ H ⇤ z, G(z)
G(x) + ⌅u, z
x⇧}
G(x) = |x|
Smooth functions:
If F is C 1 , F (x) = { F (x)}
G(0) = [ 1, 1]
First-order conditions:
x
argmin G(x)
0
x H
Monotone operator:
(u, v)
U (x)
G(x )
U (x)
x
U (x) = G(x)
U (y),
y
x, v
u
0

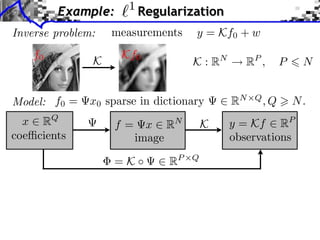
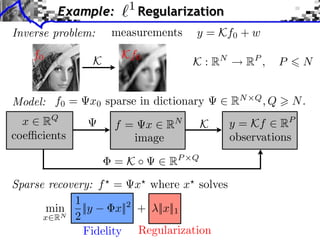
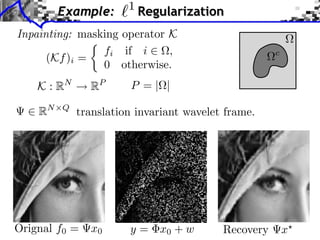
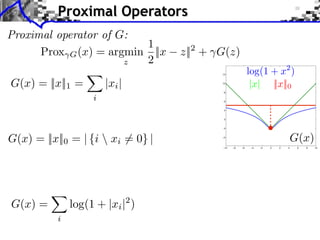
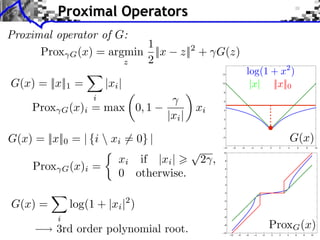
16. Example:
1
Regularization
1
x ⇥ argmin G(x) = ||y
2
x RQ
⇥G(x) =
|| · ||1 (x)i =
( x
y) + ⇥|| · ||1 (x)
x||2 + ||x||1
sign(xi ) if xi ⇥= 0,
[ 1, 1] if xi = 0.

17. Example:
1
Regularization
1
x ⇥ argmin G(x) = ||y
2
x RQ
⇥G(x) =
|| · ||1 (x)i =
( x
x||2 + ||x||1
y) + ⇥|| · ||1 (x)
sign(xi ) if xi ⇥= 0,
[ 1, 1] if xi = 0.
Support of the solution:
I = {i ⇥ {0, . . . , N 1} xi ⇤= 0}
xi
i

18. Example:
1
Regularization
1
x ⇥ argmin G(x) = ||y
2
x RQ
⇥G(x) =
|| · ||1 (x)i =
( x
x||2 + ||x||1
y) + ⇥|| · ||1 (x)
sign(xi ) if xi ⇥= 0,
[ 1, 1] if xi = 0.
xi
i
Support of the solution:
I = {i ⇥ {0, . . . , N 1} xi ⇤= 0}
First-order conditions:
s
RN ,
( x
i,
y) + s = 0
sI = sign(xI ),
||sI c ||
1.
y
x
i

19. Example: Total Variation Denoising
Important: the optimization variable is f .
1
f ⇥ argmin ||y f ||2 + J(f )
f RN 2
Finite di erence gradient:
Discrete TV norm:
:R
J(f ) =
i
= 0 (noisy)
N
R
N 2
||( f )i ||
( f )i
R2

20. Example: Total Variation Denoising
1
f ⇥ argmin ||y
f RN 2
J(f ) = G( f )
f ||2 + J(f )
G(u) =
i
Composition by linear maps:
J(f ) =
⇥G(u)i =
(J
||ui ||
A) = A
( J) A
div ( G( f ))
ui
||ui ||
if ui ⇥= 0,
R2 || || 1
if ui = 0.

21. Example: Total Variation Denoising
1
f ⇥ argmin ||y
f RN 2
J(f ) = G( f )
f ||2 + J(f )
G(u) =
i
(J
Composition by linear maps:
J(f ) =
⇥G(u)i =
A) = A
( J) A
div ( G( f ))
if ui ⇥= 0,
R2 || || 1
ui
||ui ||
First-order conditions:
⇥i
⇥i
||ui ||
I, vi =
I c , ||vi ||
v
fi
|| fi || ,
1
RN
if ui = 0.
2
, f = y + div(v)
I = {i (⇥f )i = 0}

22. Overview
• Subdifferential Calculus
• Proximal Calculus
• Forward Backward
• Douglas Rachford
• Generalized Forward-Backward
• Duality

23. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x
2
z
z||2 + G(z)

24. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x
2
z
G(x) = ||x||1 =
z||2 + G(z)
log(1 + x2 )
|x| ||x||0
12
i
|xi |
10
8
6
4
2
0
G(x) = ||x||0 = | {i xi = 0} |
G(x) =
i
log(1 + |xi |2 )
G(x)
−2
−10
−8
−6
−4
−2
0
2
4
6
8
10

25. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x
2
z
G(x) = ||x||1 =
Prox
G (x)i
z||2 + G(z)
12
i
|xi |
= max 0, 1
10
8
|xi |
G(x) = ||x||0 = | {i xi = 0} |
Prox
G (x)i
log(1 + x2 )
|x| ||x||0
=
xi if |xi |
0 otherwise.
xi
6
4
2
0
G(x)
−2
−10
2 ,
−8
−6
−4
−2
0
2
4
6
8
10
10
8
6
4
2
0
G(x) =
i
log(1 + |xi |2 )
3rd order polynomial root.
−2
−4
−6
ProxG (x)
−8
−10
−10
−8
−6
−4
−2
0
2
4
6
8
10

26. Proximal Calculus
Separability:
G(x) = G1 (x1 ) + . . . + Gn (xn )
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))

27. Proximal Calculus
Separability:
G(x) = G1 (x1 ) + . . . + Gn (xn )
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))
1
Quadratic functionals:
G(x) = || x y||2
2
Prox G = (Id +
) 1
=
(Id +
)
1

28. Proximal Calculus
Separability:
G(x) = G1 (x1 ) + . . . + Gn (xn )
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))
1
Quadratic functionals:
G(x) = || x y||2
2
Prox G = (Id +
) 1
=
(Id +
)
1
Composition by tight frame: A A = Id
ProxG
A (x)
=A
ProxG A + Id
A
A

29. Proximal Calculus
G(x) = G1 (x1 ) + . . . + Gn (xn )
Separability:
ProxG (x) = (ProxG1 (x1 ), . . . , ProxGn (xn ))
1
Quadratic functionals:
G(x) = || x y||2
2
Prox G = (Id +
) 1
=
(Id +
)
1
Composition by tight frame: A A = Id
ProxG
A (x)
Indicators:
Prox
G (x)
=A
G(x) =
ProxG A + Id
z C
A
x
C (x)
= ProjC (x)
= argmin ||x
A
C
z||
ProjC (x)

30. Prox and Subdifferential
Resolvant of G:
z = Prox
x
G (x)
0
(Id + ⇥G)(z)
z
x + ⇥G(z)
z = (Id + ⇥G)
1
(x)
Inverse of a set-valued mapping:
where x
Prox
G
U (y)
= (Id + ⇥G)
y
1
U
1
(x)
is a single-valued mapping

31. Prox and Subdifferential
Resolvant of G:
z = Prox
x
G (x)
0
(Id + ⇥G)(z)
z
x + ⇥G(z)
z = (Id + ⇥G)
1
(x)
Inverse of a set-valued mapping:
where x
Prox
G
Fix point:
U (y)
= (Id + ⇥G)
x
y
1
U
(x)
is a single-valued mapping
argmin G(x)
x
0
1
G(x )
x⇥ = (Id + ⇥G)
x
1
(Id + ⇥G)(x )
(x⇥ ) = Prox
(x⇥ )
G

32. Gradient and Proximal Descents
x( +1) = x( )
G(x( ) )
Gradient descent:
G is C 1 and G is L-Lipschitz
Theorem:
If 0 <
< 2/L, x(
)
[explicit]
x a solution.

33. Gradient and Proximal Descents
x( +1) = x( )
G(x( ) )
Gradient descent:
G is C 1 and G is L-Lipschitz
Theorem:
< 2/L, x(
If 0 <
Sub-gradient descent: x(
Theorem:
If
+1)
= x(
1/⇥, x(
Problem: slow.
)
)
)
[explicit]
x a solution.
v( ) ,
v(
)
x a solution.
G(x( ) )

34. Gradient and Proximal Descents
x( +1) = x( )
G(x( ) )
Gradient descent:
G is C 1 and G is L-Lipschitz
Theorem:
< 2/L, x(
If 0 <
Sub-gradient descent: x(
Theorem:
+1)
= x(
1/⇥, x(
If
)
)
[explicit]
x a solution.
v( ) ,
v(
)
G(x( ) )
x a solution.
)
Problem: slow.
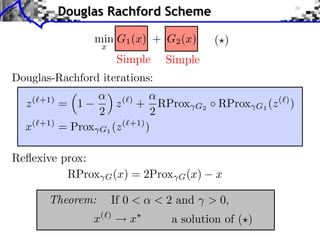
Proximal-point algorithm: x(⇥+1) = Prox
Theorem:
c > 0, x(
If
Prox
G
)
(x(⇥) ) [implicit]
G
x a solution.
hard to compute.

35. Overview
• Subdifferential Calculus
• Proximal Calculus
• Forward Backward
• Douglas Rachford
• Generalized Forward-Backward
• Duality

36. Proximal Splitting Methods
Solve
Problem:
Prox
min E(x)
x H
E
is not available.

37. Proximal Splitting Methods
Solve
min E(x)
x H
is not available.
Problem:
Prox
Splitting:
E(x) = F (x) +
E
Smooth
Gi (x)
i
Simple

38. Proximal Splitting Methods
Solve
min E(x)
x H
is not available.
Problem:
Prox
Splitting:
E(x) = F (x) +
E
Smooth
Gi (x)
i
Iterative algorithms using:
Forward-Backward:
solves
Simple
F (x)
Prox Gi (x)
F + G
Douglas-Rachford:
Gi
Primal-Dual:
Gi A
Generalized FB:
F+
Gi

39. Smooth + Simple Splitting
Inverse problem:
f0
K
Model: f0 =
measurements
Kf0
y = Kf0 + w
K : RN
x0 sparse in dictionary
Sparse recovery: f =
RP ,
P
.
x where x solves
min F (x) + G(x)
x RN
Smooth Simple
1
Data fidelity:
F (x) = ||y
x||2
2
Regularization: G(x) = ||x||1 =
|xi |
i
=K ⇥
N

40. Forward-Backward
Fix point equation:
x
argmin F (x) + G(x)
x
(x
0
F (x ) + G(x )
F (x ))
x + ⇥G(x )
x⇥ = Prox
(x⇥
G
F (x⇥ ))

41. Forward-Backward
Fix point equation:
x
argmin F (x) + G(x)
x
(x
0
F (x ) + G(x )
F (x ))
x + ⇥G(x )
x⇥ = Prox
Forward-backward:
x(⇥+1) = Prox
(x⇥
G
G
x(⇥)
F (x⇥ ))
F (x(⇥) )

42. Forward-Backward
Fix point equation:
x
argmin F (x) + G(x)
x
(x
0
F (x ) + G(x )
F (x ))
x + ⇥G(x )
x⇥ = Prox
Forward-backward:
(x⇥
G
x(⇥+1) = Prox
Projected gradient descent:
G=
G
C
x(⇥)
F (x⇥ ))
F (x(⇥) )

43. Forward-Backward
Fix point equation:
x
argmin F (x) + G(x)
x
F (x ) + G(x )
F (x ))
(x
0
x + ⇥G(x )
x⇥ = Prox
Forward-backward:
x(⇥+1) = Prox
G=
Projected gradient descent:
Theorem:
If
< 2/L,
(x⇥
G
Let
x(
)
G
x(⇥)
F (x⇥ ))
F (x(⇥) )
C
F be L-Lipschitz.
x
a solution of ( )

44. Example: L1 Regularization
1
min || x
x 2
y||2 + ||x||1
1
F (x) = || x
2
min F (x) + G(x)
x
y||2
F (x) =
( x
G(x) = ||x||1
Prox
G (x)i
Forward-backward
L = ||
y)
= max 0, 1
⇥
|xi |
||
xi
Iterative soft thresholding

45. Convergence Speed
min E(x) = F (x) + G(x)
x
F is L-Lipschitz.
G is simple.
Theorem:
If L > 0, FB iterates x(
E(x( ) )
E(x )
C degrades with L
C/
0.
)
satisfies

46. Multi-steps Accelerations
t(0) = 1
Beck-Teboule accelerated FB:
✓
◆
1
(`+1)
(`)
x
= Prox1/L y
rF (y (`) )
L
1+
1 + 4(t( ) )2
t( +1) =
2()
t
1 (
( +1)
( +1)
y
=x
+ ( +1) (x
t
+1)
x( ) )
(see also Nesterov method)
Theorem:
If L > 0,
( )
E(x
)
E(x )
C
Complexity theory: optimal in a worse-case sense.

47. Overview
• Subdifferential Calculus
• Proximal Calculus
• Forward Backward
• Douglas Rachford
• Generalized Forward-Backward
• Duality

48. Douglas Rachford Scheme
min G1 (x) + G2 (x)
x
Simple
( )
Simple
Douglas-Rachford iterations:
z (⇥+1) = 1
x(`+1)
2
z (⇥) +
2
= Prox G1 (z (`+1) )
Reflexive prox:
RProx
G (x)
RProx
= 2Prox
G2
G (x)
RProx
x
(z (⇥) )
G1

49. Douglas Rachford Scheme
min G1 (x) + G2 (x)
x
Simple
( )
Simple
Douglas-Rachford iterations:
z (⇥+1) = 1
x(`+1)
z (⇥) +
2
2
= Prox G1 (z (`+1) )
Reflexive prox:
RProx
Theorem:
x(
G (x)
= 2Prox
If 0 <
)
RProx
x
G2
G (x)
RProx
x
< 2 and ⇥ > 0,
a solution of ( )
(z (⇥) )
G1

50. DR Fix Point Equation
min G1 (x) + G2 (x)
0
x
z, z
x
x = Prox
(G1 + G2 )(x)
⇥( G1 )(x) and x
G1 (z)
and
(2x
z)
⇥( G2 )(x)
z
x
⇥( G2 )(x)

51. DR Fix Point Equation
min G1 (x) + G2 (x)
0
x
z, z
⇥( G1 )(x) and x
x
x = Prox
(G1 + G2 )(x)
G1 (z)
x = Prox
and
(2x
⇥( G2 )(x)
z
G2
⇥( G2 )(x)
x
z) = Prox
G2 (2x
z)
RProx
G1 (z)
z = 2Prox
G2
RProx
G1 (y)
(2x
z = 2Prox
G2
RProx
G1 (z)
RProx
G1 (z)
RProx
G1 (z)
z = RProx
z= 1
2
G2
RProx
z+
2
z)
G1 (z)
RProx
G2

52. Example: Constrainted L1
min ||x||1
min G1 (x) + G2 (x)
x=y
C = {x x = y}
G1 (x) = iC (x),
Prox
x
G1 (x) = ProjC (x) = x +
G2 (x) = ||x||1
Prox
e⇥cient if
G2 (x)
=
⇥
(
⇥
)
max 0, 1
easy to invert.
1
(y
|xi |
x)
xi
i

53. Example: Constrainted L1
min ||x||1
min G1 (x) + G2 (x)
x=y
C = {x x = y}
G1 (x) = iC (x),
Prox
x
G1 (x) = ProjC (x) = x +
G2 (x) = ||x||1
Prox
e⇥cient if
G2 (x)
=
⇥
(
easy to invert.
Example: compressed sensing
y = x0
400
Gaussian matrix
||x0 ||0 = 17
)
1
max 0, 1
1
R100
⇥
(y
x)
xi
|xi |
i
log10 (||x( ) ||1
||x ||1 )
0
−1
−2
−3
−4
−5
= 0.01
=1
= 10
50
100
150
200
250

54. More than 2 Functionals
min G1 (x) + . . . + Gk (x)
x
min
(x1 ,...,xk )
each Fi is simple
G(x1 , . . . , xk ) + ◆C (x1 , . . . , xk )
G(x1 , . . . , xk ) = G1 (x1 ) + . . . + Gk (xk )
C = (x1 , . . . , xk )
Hk x1 = . . . = xk

55. More than 2 Functionals
each Fi is simple
min G1 (x) + . . . + Gk (x)
x
min
(x1 ,...,xk )
G(x1 , . . . , xk ) + ◆C (x1 , . . . , xk )
G(x1 , . . . , xk ) = G1 (x1 ) + . . . + Gk (xk )
C = (x1 , . . . , xk )
G and
Prox
Prox
C
Hk x1 = . . . = xk
are simple:
G (x1 , . . . , xk )
= (Prox
Gi (xi ))i
⇥C (x1 , . . . , xk )
= (˜, . . . , x)
x
˜
1
where x =
˜
k
xi
i

56. Auxiliary Variables: DR
Linear map A : E
min G1 (x) + G2 A(x)
x
min G(z) +
z⇥H E
G1 , G2 simple.
C (z)
G(x, y) = G1 (x) + G2 (y)
C = {(x, y) ⇥ H
E Ax = y}
H.

57. Auxiliary Variables: DR
Linear map A : E
min G1 (x) + G2 A(x)
x
min G(z) +
z⇥H E
G1 , G2 simple.
C (z)
G(x, y) = G1 (x) + G2 (y)
C = {(x, y) ⇥ H
Prox
G (x, y)
= (Prox
G1 (x), Prox G2 (y))
˜
Prox C (x, y) = (x + A y , y
where
E Ax = y}
x x
y ) = (˜, A˜)
˜
y = (Id + AA )
˜
1
(Ax
x = (Id + A A)
˜
1
(A y + x)
y)
e cient if Id + AA or Id + A A easy to invert.
H.

58. Example: TV Regularization
1
min ||Kf y||2 + ||⇥f ||1
f
2
min G1 (f ) + G2
(f )
||u||1 =
i
||ui ||
x
G1 (u) = ||u||1
1
G2 (f ) = ||Kf
2
C = (f, u) ⇥ RN
Prox
G1 (u)i
y||2
RN
Prox
2
= max 0, 1
G2
u = ⇤f
˜ ˜
Prox C (f, u) = (f , f )
||ui ||
= (Id + K K)
ui
1
K

59. Example: TV Regularization
1
min ||Kf y||2 + ||⇥f ||1
f
2
min G1 (f ) + G2
(f )
||u||1 =
i
||ui ||
x
G1 (u) = ||u||1
1
G2 (f ) = ||Kf
2
C = (f, u) ⇥ RN
Prox
G1 (u)i
y||2
RN
Prox
2
= max 0, 1
G2
||ui ||
= (Id + K K)
ui
1
K
u = ⇤f
˜ ˜
Prox C (f, u) = (f , f )
Compute the solution of:
(Id +
˜
)f =
div(u) + f
O(N log(N )) operations using FFT.

60. Example: TV Regularization
Orignal f0
y = Kx0
y = f0 + w
Recovery f
Iteration

61. Overview
• Subdifferential Calculus
• Proximal Calculus
• Forward Backward
• Douglas Rachford
• Generalized Forward-Backward
• Duality

62. GFB Splitting
n
min F (x) +
x RN
(⇥+1)
(⇥)
zi
= zi +
n
1
( +1)
x
=
n
Proxn
i=1
( )
i=1
Smooth
i = 1, . . . , n,
Gi (x)
( +1)
zi
G
Simple
(2x
(⇥)
(⇥)
zi
F (x(⇥) )) x(⇥)

63. GFB Splitting
n
min F (x) +
x RN
(⇥+1)
(⇥)
zi
= zi +
n
1
( +1)
=
x
n
Simple
Proxn
G
(2x
(⇥)
(⇥)
zi
F (x(⇥) )) x(⇥)
( +1)
zi
i=1
Theorem:
If
( )
i=1
Smooth
i = 1, . . . , n,
Gi (x)
< 2/L,
Let
x(
)
F be L-Lipschitz.
x
a solution of ( )

64. GFB Splitting
n
min F (x) +
x RN
(⇥+1)
(⇥)
zi
= zi +
n
1
( +1)
=
x
n
Proxn
Simple
G
(2x
(⇥)
(⇥)
zi
F (x(⇥) )) x(⇥)
( +1)
zi
i=1
Theorem:
If
( )
i=1
Smooth
i = 1, . . . , n,
Gi (x)
< 2/L,
n=1
F =0
Let
x(
)
F be L-Lipschitz.
x
a solution of ( )
Forward-backward.
Douglas-Rachford.

65. GFB Fix Point
x
argmin F (x) +
x RN
yi
i
Gi (x)
Gi (x ),
0
F (x ) +
F (x ) +
i yi
=0
i
Gi (x )

66. GFB Fix Point
x
argmin F (x) +
x RN
i
Gi (x)
Gi (x ),
yi
(zi )n ,
i=1
1
i, x
n
x =
i zi
1
n
0
F (x ) +
zi
F (x ) +
i yi
Gi (x )
=0
F (x )
(use zi = x
i
⇥Gi (x )
F (x )
N yi )

67. GFB Fix Point
x
argmin F (x) +
x RN
i
Gi (x)
Gi (x ),
yi
(zi )n ,
i=1
i zi
1
n
(2x
zi
x⇥ = Proxn
F (x ) +
F (x ) +
1
i, x
n
x =
0
i yi
(use zi = x
F (x ))
(2x⇥
Gi
zi = zi + Proxn
G
⇥Gi (x )
F (x )
N yi )
n ⇥Gi (x )
x
F (x⇥ ))
zi
(2x⇥
Gi (x )
=0
F (x )
zi
i
zi
F (x⇥ ))
x⇥

68. GFB Fix Point
x
argmin F (x) +
x RN
i
Gi (x)
Gi (x ),
yi
(zi )n ,
i=1
i zi
1
n
(2x
zi
x⇥ = Proxn
i yi
(use zi = x
F (x ))
(2x⇥
Gi
G
Gi (x )
⇥Gi (x )
F (x )
N yi )
n ⇥Gi (x )
x
F (x⇥ ))
zi
(2x⇥
i
=0
F (x )
zi
zi = zi + Proxn
+
F (x ) +
F (x ) +
1
i, x
n
x =
0
zi
F (x⇥ ))
x⇥
Fix point equation on (x , z1 , . . . , zn ).

69. Block Regularization
1
2
block sparsity: G(x) =
b B
iments
2
+
(2)
` 1 `2
4
k=1
N: 256
x
x2
m
m b
Towards More Complex Penalization
Bk
1,2
⇥ x⇥⇥1 =
i ⇥xi ⇥
b
Image f =
||x[b] ||2 =
||x[b] ||,
B
x Coe cients x.
b B
i
xi2
b
b B1
b B2
+
i b xi
i b xi

70. Block Regularization
1
2
block sparsity: G(x) =
b B
||x[b] ||,
||x[b] ||2 =
x2
m
m b
... B
Non-overlapping decomposition: B = B
iments Towards More Complex Penalization
Towards More Complex Penalization
Towards More Complex Penalization
2
1
n
(2)
G(x) =4 x iBk
(x)
+ ` ` k=1 G 1,2
1
2
N: 256
Gi (x) =
b Bi
i=1
⇥=
⇥ x⇥x⇥x⇥⇥1 =i ⇥x⇥x⇥xi ⇥
⇥ ⇥1 ⇥1 = i i ⇥i i ⇥
b
Image f =
||x[b] ||,
bb B B i
Bb
xii2bi2xi2
bbx
i
B
x Coe cients x.
n
Blocks B1
22
b b 1b1 B1 i b xiixb xi
BB
i b i
++ +
b b 2b2 B2 i
BB
B1
xi2 b2xi
b b xi
i
B2

71. Block Regularization
1
2
block sparsity: G(x) =
b B
||x[b] ||,
||x[b] ||2 =
x2
m
m b
... B
Non-overlapping decomposition: B = B
iments Towards More Complex Penalization
Towards More Complex Penalization
Towards More Complex Penalization
2
1
n
(2)
G(x) =4 x iBk
(x)
+ ` ` k=1 G 1,2
1
2
Gi (x) =
b Bi
i=1
||x[b] ||,
Each Gi is simple:
⇥ ⇥1 = i ⇥i i
⇥ x⇥x⇥x⇥⇥1 =i ⇥xG ⇥xi ⇥ m = b B B i b xii2bi2xi2
=
Bb
⇤ m ⇥ b ⇥ Bi , ⇥ ⇥1Prox i ⇥xi ⇥(x) b max i0, 1
bx
N: 256
b
Image f =
B
x Coe cients x.
n
Blocks B1
22
b b 1b1 B1 i b xiixb xi
BB
i b i
||x[b]b||B
b B b
++m
x +
2 2 B2
B1
i
xi2 b2xi
b b xi
i
B2

72. 10
10
x+1,2`
1
`2
k=1
Numerical
Numerical Experiments Experiments
1
1
1
0
log10(E−Emin)
log10(E−Emin)
tmin
: 283s; t : 298s; t :: 283s; t : 298s; t (2)
t CP 2 +
368s
||y x 1 ⇥x||368s PRx 2 minix(x)Y ⇥ K
PR
Deconvolution +GCP: 1` 4
−1 EFB
−1 EFB
Deconvolution min 2 Y ⇥ K
`
x 102
10 40
20
30 1 2 2 40k=1
20
30
EFB iteration #
i
EFB
iteration 3
#
3
0
log10(E−Emin)
x
k=1
Numerical Illustration
log (E−
log (E−E
Deconv. + Inpaint. 2min+CP Y ⇥ P K x CP Y + P 1 K2
x
Deconv. x 2Inpaint. min 2 ⇥ ` `
2
PR
CP
= convolution
2
x
PR
CP 2
λ
Bk 2
TI (2)`2 4
x= + `wavelets x
k=1
1,2
1
λ2 : 1.30e−03;
: 1.30e−03;
= inpainting+convolution l1/l2
l1/l2
tEFB: 161s; tPR: 173s; tCP N: 256
190s
t
: 161s; noise: 0.025; :convol.: 2
t : 173s; t
190s noise: 0.025; convol.::it. #50; SNR: 22.49dB #50; SNR: 22.49dB
it.
2
N: 256
EFB
PR
CP
3
2
Numerical Experiments
1
0
onv. + Inpaint. minx
2
10
20
1
EFB
0
3
PR
1
CP
2 30
2
1
iteration #
1
0
0
Y ⇥P K
10
40
20
x
2
+
30
iteration #
EFB
PR
(4)
CP
`140`2
16
k=1
x
λ4 : 1.00e−03;
l1/l2
Bk
1,2
λ4 : 1.00e−03;
l1/l2
10
min
tEFB: 283s; tPR: 298s; tCP: 368s
it. #50; SNR: 21.80dB #50; SNR: 21.80dB
noise: 0.025; degrad.: 0.4; 0.025; degrad.: 0.4; convol.: 2
it.
noise: convol.: 2
−1
−1
10
20
30
EFB
PR
CP
iteration #
3
2
1
40
10
20
30
x0
40
iteration #
λ2
: 1.30e−03;
l1/l2
noise: 0.025; it. #50; SNR: 22.49dB
convol.: 2
noise: 0.025; convol.: 2
0
10
log10
20
iteration
(E(x( ) ) #
y = x0 + w
E(x ))
30
40
4
x
λ2 : 1.30e−03;
l1/l2
it. #50; SNR: 22.49dB

73. Overview
• Subdifferential Calculus
• Proximal Calculus
• Forward Backward
• Douglas Rachford
• Generalized Forward-Backward
• Duality

74. Legendre-Fenchel Duality
Legendre-Fenchel transform:
G (u) =
sup
x dom(G)
u, x
G(x)
eu
lop
S
G(x)
G (u)
x

75. Legendre-Fenchel Duality
Legendre-Fenchel transform:
G (u) =
sup
u, x
G(x)
x dom(G)
Example: quadratic functional
1
G(x) = Ax, x + x, b
2
1
G (u) = u b, A 1 (u b)
2
eu
lop
S
G(x)
G (u)
x

76. Legendre-Fenchel Duality
Legendre-Fenchel transform:
G (u) =
sup
u, x
G(x)
x dom(G)
Example: quadratic functional
1
G(x) = Ax, x + x, b
2
1
G (u) = u b, A 1 (u b)
2
G(x)
G (u)
Moreau’s identity:
Prox
G
(x) = x
G simple
eu
lop
S
ProxG/ (x/ )
G simple
x

77. Indicator and Homogeneous
Positively 1-homogeneous functional:
Example: norm
Duality:
G (x) =
G(x) = ||x||
G (·) 1 (x)
G( x) = |x|G(x)
G (y) = min
G(x) 1
x, y

78. Indicator and Homogeneous
Positively 1-homogeneous functional:
Example: norm
Duality:
G (x) =
G(x) = ||x||
G (·) 1 (x)
G( x) = |x|G(x)
G (y) = min
G(x) 1
p
norms:
G(x) = ||x||p
G (x) = ||x||q
1 1
+ =1
p q
1
x, y
p, q
+

79. Indicator and Homogeneous
G( x) = |x|G(x)
Positively 1-homogeneous functional:
G(x) = ||x||
Example: norm
Duality:
G (x) =
G (·) 1 (x)
G (y) = min
G(x) 1
p
norms:
G(x) = ||x||p
G (x) = ||x||q
1 1
+ =1
p q
Example: Proximal operator of
Prox
||·||
Proj||·||1
= Id
norm
Proj||·||1
(x)i = max 0, 1
|xi |
for a well-chosen ⇥ = ⇥ (x, )
xi
1
x, y
p, q
+

80. Primal-dual Formulation
A:H⇥
Fenchel-Rockafellar duality:
L
linear
min G1 (x) + G2 A(x) = min G1 (x) + sup hAx, ui
x2H
x
u2L
G⇤ (u)
2

81. Primal-dual Formulation
A:H⇥
Fenchel-Rockafellar duality:
L
linear
min G1 (x) + G2 A(x) = min G1 (x) + sup hAx, ui
x
x2H
u2L
G⇤ (u)
2
Strong duality:
0 2 ri(dom(G2 ))
(min $ max)
= max
G⇤ (u) + min G1 (x) + hx, A⇤ ui
2
= max
G⇤ (u)
2
u
u
A ri(dom(G1 ))
x
G⇤ (
1
A⇤ u)

82. Primal-dual Formulation
A:H⇥
Fenchel-Rockafellar duality:
L
linear
min G1 (x) + G2 A(x) = min G1 (x) + sup hAx, ui
x
x2H
u2L
G⇤ (u)
2
Strong duality:
0 2 ri(dom(G2 ))
(min $ max)
= max
G⇤ (u) + min G1 (x) + hx, A⇤ ui
2
= max
G⇤ (u)
2
u
u
A ri(dom(G1 ))
x
G⇤ (
1
Recovering x? from some u? :
x? = argmin G1 (x? ) + hx? , A⇤ u? i
x
A⇤ u)

83. Primal-dual Formulation
A:H⇥
Fenchel-Rockafellar duality:
L
linear
min G1 (x) + G2 A(x) = min G1 (x) + sup hAx, ui
x
x2H
u2L
G⇤ (u)
2
Strong duality:
0 2 ri(dom(G2 ))
(min $ max)
= max
G⇤ (u) + min G1 (x) + hx, A⇤ ui
2
= max
G⇤ (u)
2
u
u
A ri(dom(G1 ))
x
G⇤ (
1
A⇤ u)
Recovering x? from some u? :
x? = argmin G1 (x? ) + hx? , A⇤ u? i
x
()
A⇤ u? 2 @G1 (x? )
() x? 2 (@G1 )
1
( A⇤ u? ) = @G⇤ ( A⇤ u? )
1

84. Forward-Backward on the Dual
If G1 is strongly convex:
G1 (tx + (1
r2 G1 > cId
t)y) 6 tG1 (x) + (1
t)G1 (y)
c
t(1
2
t)||x
y||2

85. Forward-Backward on the Dual
If G1 is strongly convex:
G1 (tx + (1
r2 G1 > cId
t)y) 6 tG1 (x) + (1
x? uniquely defined.
G? is of class C 1 .
1
t)G1 (y)
c
t(1
2
t)||x
x? = rG? ( A⇤ u? )
1
y||2

86. Forward-Backward on the Dual
r2 G1 > cId
If G1 is strongly convex:
G1 (tx + (1
t)y) 6 tG1 (x) + (1
x? uniquely defined.
G? is of class C 1 .
1
FB on the dual:
t)G1 (y)
c
t(1
2
t)||x
x? = rG? ( A⇤ u? )
1
min G1 (x) + G2 A(x)
x2H
=
min G? ( A⇤ u) + G? (u)
1
2
u2L
Simple
Smooth
⇣
u(`+1) = Prox⌧ G? u(`) + ⌧ A⇤ rG? ( A⇤ u(`) )
1
2
⌘
y||2

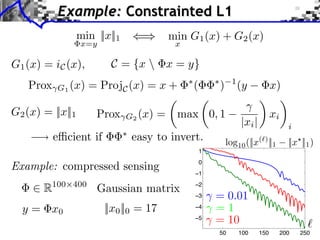
87. Example: TV Denoising
1
min ||f
f RN 2
y||2 + ||⇥f ||1
||u||1 =
Dual solution u
i
||ui ||
min ||y + div(u)||2
||u||
||u||
= max ||ui ||
i
Primal solution f = y + div(u )
[Chambolle 2004]

88. Example: TV Denoising
1
min ||f
f RN 2
min ||y + div(u)||2
y||2 + ||⇥f ||1
||u||1 =
Dual solution u
i
||u||
||u||
||ui ||
+1)
= Proj||·||
i
Primal solution f = y + div(u )
FB (aka projected gradient descent):
u(
= max ||ui ||
u( ) +
[Chambolle 2004]
(y + div(u( ) ))
ui
v = Proj||·||
(u)
vi =
max(||ui ||/ , 1)
2
1
<
=
Convergence if
||div ⇥||
4

89. Primal-Dual Algorithm
min G1 (x) + G2 A(x)
x H
() min max G1 (x)
x
z
G⇤ (z) + hA(x), zi
2

90. Primal-Dual Algorithm
min G1 (x) + G2 A(x)
x H
G⇤ (z) + hA(x), zi
2
() min max G1 (x)
x
z
z (`+1) = Prox
G⇤
2
x(⇥+1) = Prox
(x(⇥)
G1
x(
˜
+ (x(
+1)
= x(
+1)
(z (`) + A(˜(`) )
x
A (z (⇥) ))
+1)
x( ) )
= 0: Arrow-Hurwicz algorithm.
= 1: convergence speed on duality gap.

91. Primal-Dual Algorithm
min G1 (x) + G2 A(x)
x H
G⇤ (z) + hA(x), zi
2
() min max G1 (x)
x
z
z (`+1) = Prox
G⇤
2
x(⇥+1) = Prox
(x(⇥)
G1
x(
˜
+ (x(
+1)
= x(
+1)
(z (`) + A(˜(`) )
x
A (z (⇥) ))
+1)
x( ) )
= 0: Arrow-Hurwicz algorithm.
= 1: convergence speed on duality gap.
Theorem: [Chambolle-Pock 2011]
If 0
x(
)
1 and ⇥⇤ ||A||2 < 1 then
x minimizer of G1 + G2 A.

92. Conclusion
Inverse problems in imaging:
Large scale, N 106 .
Non-smooth (sparsity, TV, . . . )
(Sometimes) convex.
Highly structured (separability,
p
norms, . . . ).

93. Conclusion
Inverse problems in imaging:
Large scale, N 106 .
Towards More Complex Penalization
Non-smooth (sparsity, TV, . . . )
(Sometimes) convex.
⇥ x⇥⇥1 =
i ⇥xi ⇥
b B
Highly structured (separability,
b B1
2
i p xi
b
+
2
i b xi
norms, . . . ).
b B2
Proximal splitting:
Unravel the structure of problems.
Parallelizable.
Decomposition G =
k
Gk
i
xi2
b

94. Conclusion
Inverse problems in imaging:
Large scale, N 106 .
Towards More Complex Penalization
Non-smooth (sparsity, TV, . . . )
(Sometimes) convex.
⇥ x⇥⇥1 =
i ⇥xi ⇥
b B
Highly structured (separability,
2
i p xi
b
Proximal splitting:
Unravel the structure of problems.
b B1
+
2
i b xi
norms, . . . ).
b B2
Parallelizable.
Open problems:
Less structured problems without smoothness.
Decomposition G = k Gk
Non-convex optimization.
i
xi2
b