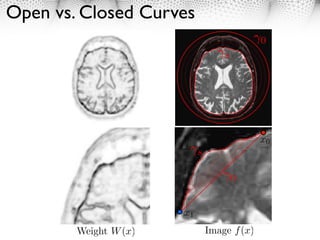
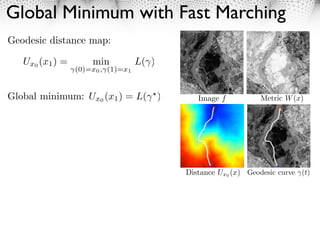
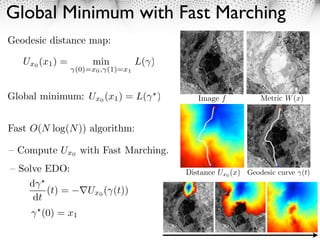
(1) Active contours, or snakes, are parametric or geometric active contour models used for edge detection and image segmentation. (2) Parametric active contours represent curves explicitly through parameterization, while implicit active contours represent curves as the zero level set of a higher dimensional function. (3) Active contours evolve to minimize an energy functional comprising an internal regularization term and an external image-based term, converging to object boundaries or other image features.

1. Active Contours
www.numerical-tours.com
Gabriel Peyré
CEREMADE, Université Paris-Dauphine

2. Overview
• Parametric Edge-based Active
Contours
• Implicit Edge-based Active Contours
• Region-based Active Contours
2

3. Parametric Active Contours
Local minimum: argmin E( ) = L( ) + ⇥R( )
Data Regularization
Boundary conditions: fidelity
x0
– Open curve: (0) = x0 and (1) = x1 .
– Closed curve: (0) = (1).
x1
3

4. Parametric Active Contours
Local minimum: argmin E( ) = L( ) + ⇥R( )
Data Regularization
Boundary conditions: fidelity
x0
– Open curve: (0) = x0 and (1) = x1 .
– Closed curve: (0) = (1).
Snakes energy: (depends on parameterization) x1
1 1
L( ) = W ( (t))|| (t)||dt, R( ) = || (t)|| + µ|| (t)||dt
0 0
Image f Weight W (x) Curve 3

5. Geodesic Active Contours
Geodesic active contours: (intrinsic) Replace W by W + ,
1
E( ) = L( ) = W ( (t))|| (t)||dt
0
(local) minimum of the weighted length L.
local geodesic (not minimal path).
Weight W (x) Curve 4

6. Curve Evolution
Family of curves { s (t)}s>0 minimizing E( s ).
s
Do not confound:
t: abscise along the curve.
s+ds
s: artificial “time” of evolution.
5

7. Curve Evolution
Family of curves { s (t)}s>0 minimizing E( s ).
s
Do not confound:
t: abscise along the curve.
s+ds
s: artificial “time” of evolution.
Local minimum of: min E( )
d
Minimization flow: s = E( s )
ds
5

8. Curve Evolution
Family of curves { s (t)}s>0 minimizing E( s ).
s
Do not confound:
t: abscise along the curve.
s+ds
s: artificial “time” of evolution.
Local minimum of: min E( )
d
Minimization flow: s = E( s )
ds
Warning: the set of curves is not a vector space.
1
Inner product at : µ, ⇥⇥ = µ(t), ⇥(t)⇥|| (t)||dt
0
Riemannian manifold of infinite dimension.
5

9. Curve Evolution
Family of curves { s (t)}s>0 minimizing E( s ).
s
Do not confound:
t: abscise along the curve.
s+ds
s: artificial “time” of evolution.
Local minimum of: min E( )
d
Minimization flow: s = E( s )
ds
Warning: the set of curves is not a vector space.
1
Inner product at : µ, ⇥⇥ = µ(t), ⇥(t)⇥|| (t)||dt
0
Riemannian manifold of infinite dimension.
Numerical implementation: (k+1)
= (k)
⇥k E( (k)
)
5

10. Intrinsic Curve Evolutions
E( ) only depends on { (t) t [0, 1]}.
Intrinsic energy E: evolution along the normal
s
d
⇥s (t) = (⇥s (t), ns (t), ⇤s (t)) ns (t) ns
ds
speed normal
s (t)
Normal: ns (t) =
|| s (t)||
1
Curvature: ⇥s (t) = ns (t), s (t)⇥
|| s (t)||2
6

11. Mean Curvature Motion
1
No data-fidelity: E( ) = || (t)||dt
0
d
Curve-shortening flow. s = E( s )
ds
1
(t)
E( + ⇥) = E( ) + , ⇥ (t)⇥dt + O(||⇥||)
0 || (t)||
1 d (t)
⌅E( ) : t ⇤⇥
|| (t)|| dt || (t)|| 0
Mean-curvature motion:
s
d
s (t) = ⇥s (t)ns (t)
ds
Speed: (x, n, ⇥) = ⇥
7

12. Discretization
Discretization: = { (i)}N 1
i=0 R2 , with (N ) = (0).
⇥µ, ⇥⇤ = i ⇥µ(i), ⇥(i)⇤|| (i) (i + 1)||
k
8

13. Discretization
Discretization: = { (i)}N 1
i=0 R2 , with (N ) = (0).
⇥µ, ⇥⇤ = i ⇥µ(i), ⇥(i)⇤|| (i) (i + 1)||
Discrete energy: E( ) = i || (i) (i + 1)||
k
8

14. Discretization
Discretization: = { (i)}N 1
i=0 R2 , with (N ) = (0).
⇥µ, ⇥⇤ = i ⇥µ(i), ⇥(i)⇤|| (i) (i + 1)||
Discrete energy: E( ) = i || (i) (i + 1)||
Gradient descent flow: k+1 = k ⇥k E( k )
k
E( k )
8

15. Discretization
Discretization: = { (i)}N 1
i=0 R2 , with (N ) = (0).
⇥µ, ⇥⇤ = i ⇥µ(i), ⇥(i)⇤|| (i) (i + 1)||
Discrete energy: E( ) = i || (i) (i + 1)||
Gradient descent flow: k+1 = k ⇥k E( k )
k
1
Discrete gradient: ⇥E( ) = ⇥ N ⇥( )
||⇥ ||
(⇥ )(i) = (i + 1) (i)
E( k )
(⇥ )(i) = (i 1) (i)
(i)
(N )(i) =
|| (i)||
8

16. Geodesic Active Contours Motion
Weighted length:
1
E( ) = L( ) = W ( (t))|| (t)||dt
0
Evolution:
d
⇥s (t) = (⇥s (t), ns (t), ⇤s (t)) ns (t) 0
ds
(x, n, ⇥) = W (x)⇥ W (x), n
attraction toward areas
where W is small.
s
finite di erences discretization.
Weight W (x)

17. Open vs. Closed Curves
0
s
x0
s
0
x1
Weight W (x) Image f (x)

18. Global Minimum with Fast Marching
Geodesic distance map:
Ux0 (x1 ) = min L( )
(0)=x0 , (1)=x1
Global minimum: Ux0 (x1 ) = L( ) Image f Metric W (x)
Distance Ux0 (x) Geodesic curve (t)

19. Global Minimum with Fast Marching
Geodesic distance map:
Ux0 (x1 ) = min L( )
(0)=x0 , (1)=x1
Global minimum: Ux0 (x1 ) = L( ) Image f Metric W (x)
Fast O(N log(N )) algorithm:
– Compute Ux0 with Fast Marching.
– Solve EDO: Distance Ux0 (x) Geodesic curve (t)
d
(t) = Ux0 ( (t))
dt
(0) = x1

20. Overview
• Parametric Edge-based Active Contours
• ImplicitEdge-based Active
Contours
• Region-based Active Contor
12

21. Level Sets
Level-set curve representation:
s (x) 0
{ s (t) t [0, 1]} = x R ⇥s (x) = 0 .
2
Example: circle of radius r s (x) = ||x x0 || s
Example: square of radius r s (x) = ||x x0 || s
s (x) 0

22. Level Sets
Level-set curve representation:
s (x) 0
{ s (t) t [0, 1]} = x R ⇥s (x) = 0 .
2
Example: circle of radius r s (x) = ||x x0 || s
Example: square of radius r s (x) = ||x x0 || s
s (x) 0
Union of domains: s = min( 1
s, s)
2
Intersection of domains: s = max( 1
s, s)
2
s (x) 0
s = min( 1
s, s)
2

23. Level Sets
Level-set curve representation:
s (x) 0
{ s (t) t [0, 1]} = x R ⇥s (x) = 0 .
2
Example: circle of radius r s (x) = ||x x0 || s
Example: square of radius r s (x) = ||x x0 || s
s (x) 0
Union of domains: s = min( 1
s, s)
2
Intersection of domains: s = max( 1
s, s)
2
s (x) 0
Popular choice: (signed) distance to a curve
⇥s (x) = ± min || s (t) x||
t
infinite number of mappings s s.
s = min( 1
s, s)
2

24. Level Sets Evolution
Dictionary parameteric implicit:
Position: x= s (t)
s (x)
Normal: ns (t) =
|| s (x)||
⇥s
Curvature: s (x) = div (x)
|| ⇥s ||
14

25. Level Sets Evolution
Dictionary parameteric implicit:
Position: x= s (t)
s (x)
Normal: ns (t) =
|| s (x)||
⇥s
Curvature: s (x) = div (x)
|| ⇥s ||
Evolution PDE:
d
⇥s (t) = (⇥s (t), ns (t), ⇤s (t)) ns (t)
ds
d ⇥s (x) ⇥s
⇥s (x) = || ⇥s (x)|| ⇥s (x), , div (x) .
ds || ⇥s (x)|| || ⇥s ||
All level sets evolves together.
14

26. Proof
d
Evolution PDE: ⇥s (t) = (⇥s (t), ns (t), ⇤s (t)) ns (t) ( )
ds
Definition of level-sets: t, ⇥s ( s (t)) = 0
15

27. Proof
d
Evolution PDE: ⇥s (t) = (⇥s (t), ns (t), ⇤s (t)) ns (t) ( )
ds
Definition of level-sets: t, ⇥s ( s (t)) = 0
Deriving with respect to t:
⇤ s ⇤⇥s
⇥s (x), (t) + (x) = 0 for x = s (t) ( )
⇤s ⇤s
15

28. Proof
d
Evolution PDE: ⇥s (t) = (⇥s (t), ns (t), ⇤s (t)) ns (t) ( )
ds
Definition of level-sets: t, ⇥s ( s (t)) = 0
Deriving with respect to t:
⇤ s ⇤⇥s
⇥s (x), (t) + (x) = 0 for x = s (t) ( )
⇤s ⇤s
⌅⇤s
( )+( ): (x) = (x, ns (t), ⇥s (t)) ⇤s (x), ns (t)
⌅s
15

29. Proof
d
Evolution PDE: ⇥s (t) = (⇥s (t), ns (t), ⇤s (t)) ns (t) ( )
ds
Definition of level-sets: t, ⇥s ( s (t)) = 0
Deriving with respect to t:
⇤ s ⇤⇥s
⇥s (x), (t) + (x) = 0 for x = s (t) ( )
⇤s ⇤s
⌅⇤s
( )+( ): (x) = (x, ns (t), ⇥s (t)) ⇤s (x), ns (t)
⌅s
s (x)
=
|| s (x)||
For all x on the curve,
d ⇥s (x) ⇥s
⇥s (x) = || ⇥s (x)|| ⇥s (x), , div (x) .
ds || ⇥s (x)|| || ⇥s ||
15

30. Implicit Geodesic Active Contours
Evolution PDE:
d s
s = || s ||div W .
ds || s ||
Comparison with explicit active contours:
: 2D instead of 1D equation.
+ : allows topology change.
16

31. Implicit Geodesic Active Contours
Evolution PDE:
d s
s = || s ||div W .
ds || s ||
Comparison with explicit active contours:
: 2D instead of 1D equation.
+ : allows topology change.
Re-initialization: ⇥s (x) = ± min || s (t) x||
t
Eikonal equation: || s || =1 with ⇥s ( s (t)) = 0
16

32. Multiple Fluids Dynamics
See Ron Fedkiw homepage. http://physbam.stanford.edu/ fedkiw/
Multiple gaz:
Fluid/air interface:
17

33. Overview
• Parametric Edge-based Active Contours
• Implicit Edge-based Active Contours
• Region-based Active Contours
18

34. Energy Depending on Region
Optimal segmentation [0, 1]2 = c
:
min L1 ( ) + L2 ( c
) + R( ) R( ) = | |
Data Regularization
fidelity
Chan-Vese binary model: L1 ( ) = |I(x) c1 |2 dx
More general models
19

35. Energy Depending on Region
Optimal segmentation [0, 1]2 = c
:
min L1 ( ) + L2 ( c
) + R( ) R( ) = | |
Data Regularization
fidelity
Chan-Vese binary model: L1 ( ) = |I(x) c1 |2 dx
More general models
Level set implementation: = {x (x) > 0}
2 x H(x)
Smoothed Heaviside: H (x) = atan
⇥ x
L1 ( ) ⇥ L( ) = H ( (x))||I(x) c1 ||2 dx
R( ) R( ) = ||⇥(H )(x)||dx
19

36. Descent Schemes
For a given c = (c1 , c2 ) R2 :
min Ec ( ) = H ( (x))||I(x) c1 ||2 +
⇥
H ( ⇥(x))||I(x) c2 ||2 + ||⇥(H ⇥)(x)||dx
20

37. Descent Schemes
For a given c = (c1 , c2 ) R2 :
min Ec ( ) = H ( (x))||I(x) c1 ||2 +
⇥
H ( ⇥(x))||I(x) c2 ||2 + ||⇥(H ⇥)(x)||dx
Descent with respect to :
⇥(k+1) = ⇥(k) k Ec (⇥(k) )
Ec ( ) = H ( (x))G(x)
⇥⇥
G(x) = ||I(x) 2
c1 || ||I(x) 2
c2 || div (x)
||⇥⇥||
20

38. Descent Schemes
For a given c = (c1 , c2 ) R2 :
min Ec ( ) = H ( (x))||I(x) c1 ||2 +
⇥
H ( ⇥(x))||I(x) c2 ||2 + ||⇥(H ⇥)(x)||dx
Descent with respect to :
⇥(k+1) = ⇥(k) k Ec (⇥(k) )
Ec ( ) = H ( (x))G(x)
⇥⇥
G(x) = ||I(x) 2
c1 || ||I(x) 2
c2 || div (x)
||⇥⇥||
Limit 0: ⇥Ec (⇥) { =0} (x)||⇥⇥(x)||G(x)
Numerically, use Ec ( ) = || (x)||G(x)
20

39. Update of c
Joint minimization: min Ec ( )
,c1 ,c2
21

40. Update of c
Joint minimization: min Ec ( )
,c1 ,c2
Update of : ⇥(k+1) = ⇥(k) k Ec(k) (⇥(k) )
21

41. Update of c
Joint minimization: min Ec ( )
,c1 ,c2
Update of : ⇥(k+1) = ⇥(k) k Ec(k) (⇥(k) )
Update of (c1 , c2 ):
(k+1) (k+1)
(c1 , c2 ) = argmin Ec ( (k)
)
c1 ,c2
(k+1)
c1 = c( (k) ) I(x)H( (x))dx
c( ) =
(k+1)
c2 = c( (k) ) H( (x))dx
21

42. Example of Evolution
Use de-localized initialization.
(0)
22

43. Conclusion
Curve evolution
Energy minimization
Parametric vs. level set representation.
Dictionary to translate
– curve properties.
– energy gradients.
Edge based vs. region based energies.
23