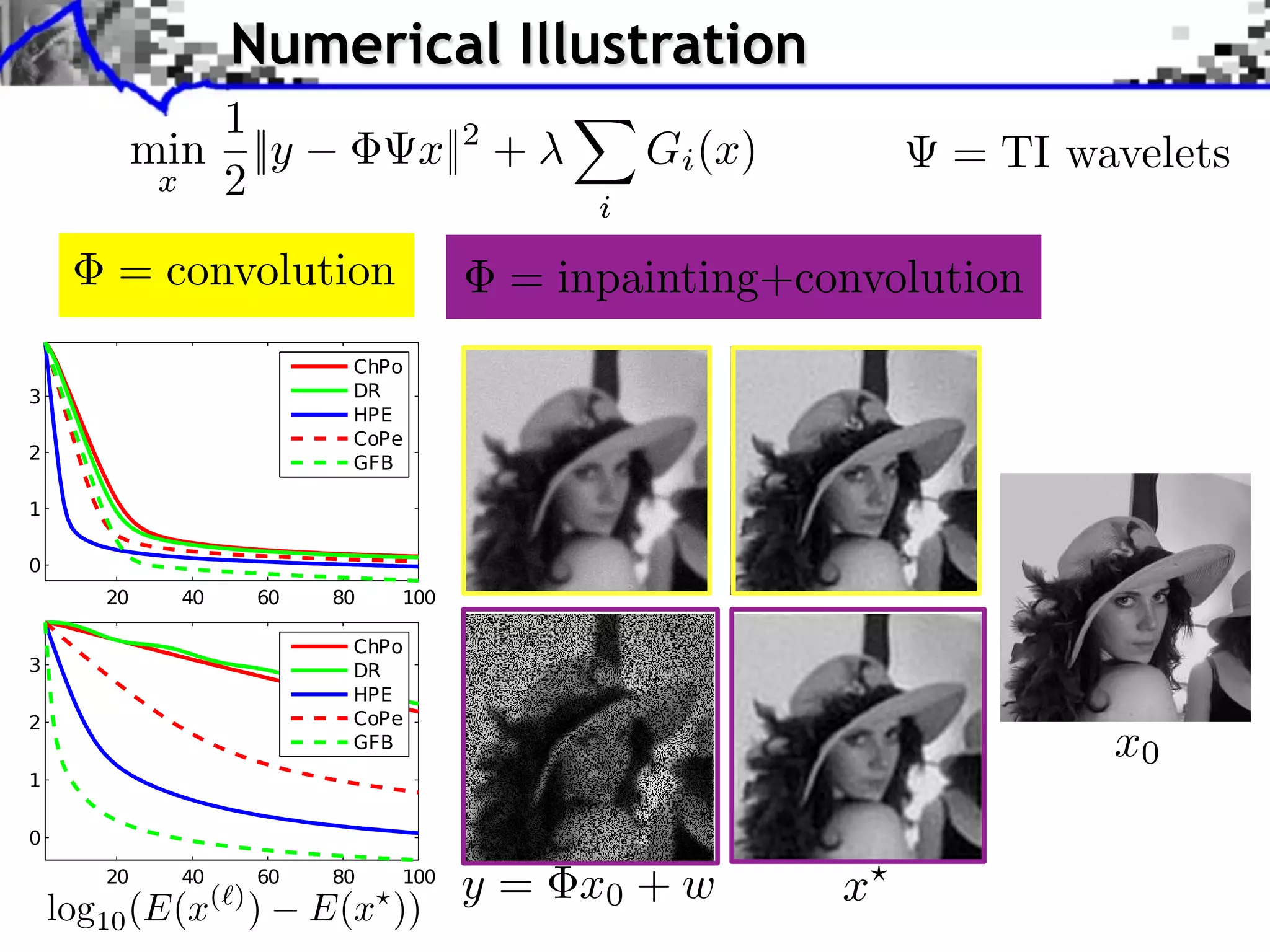
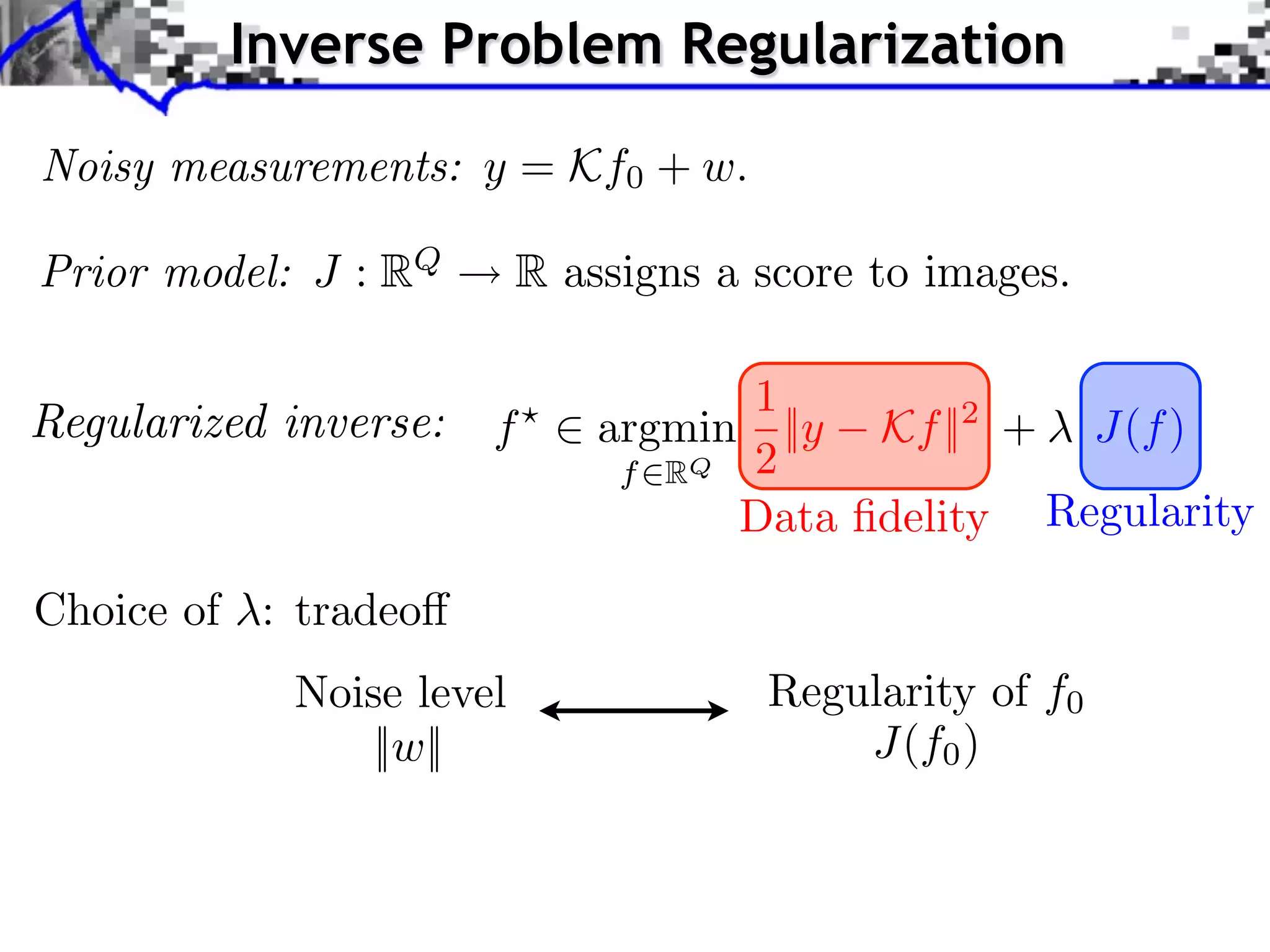
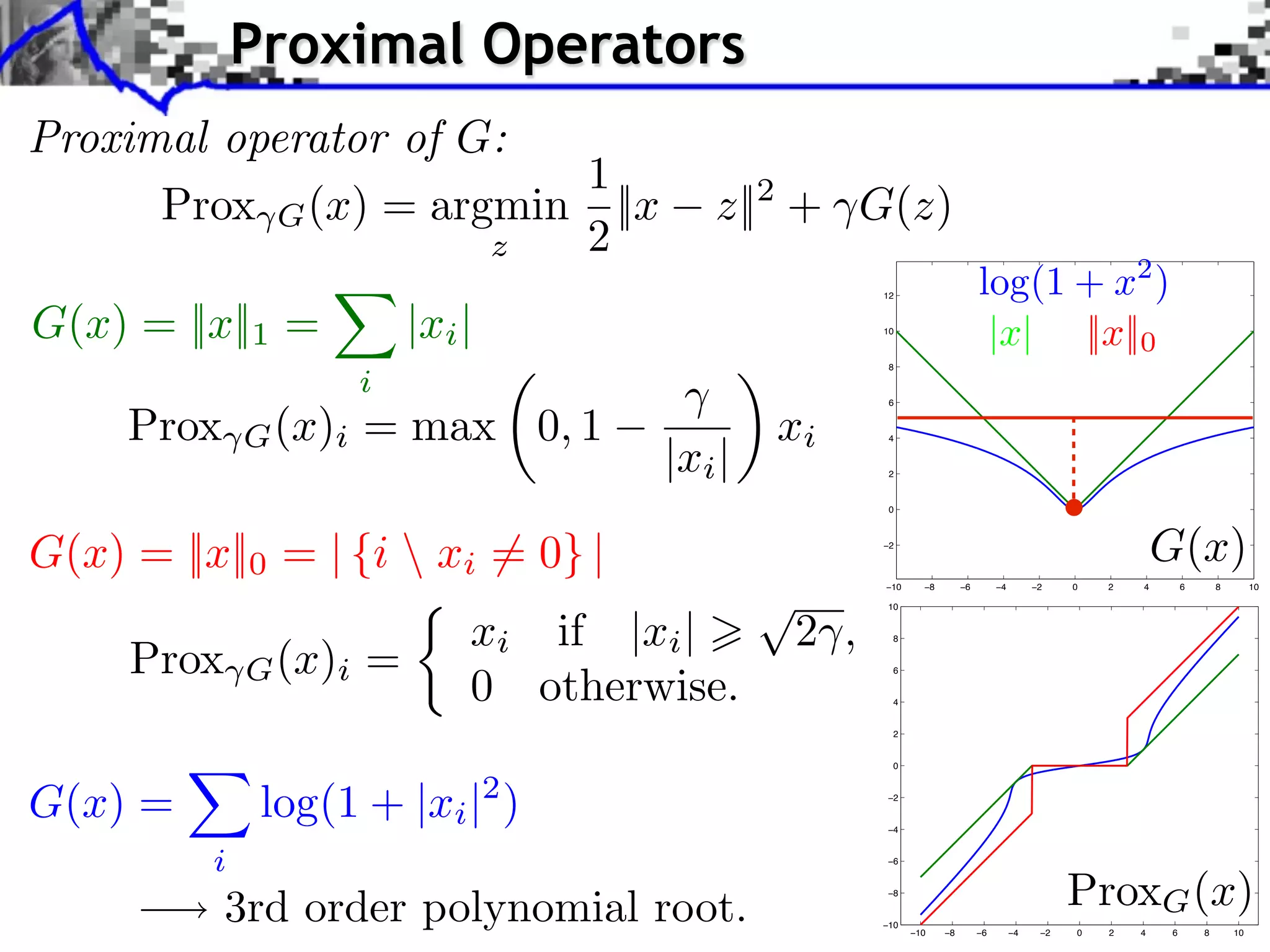
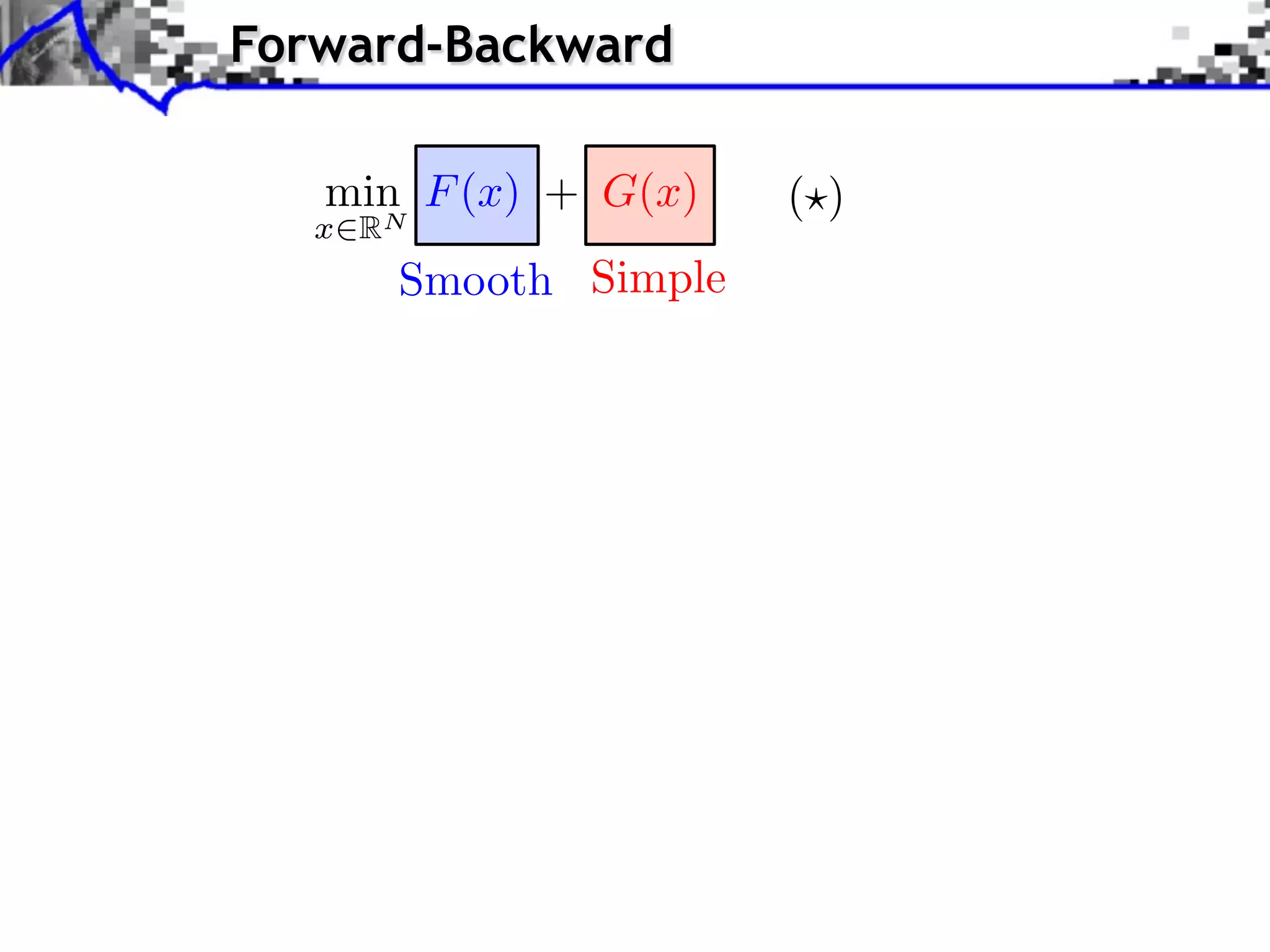
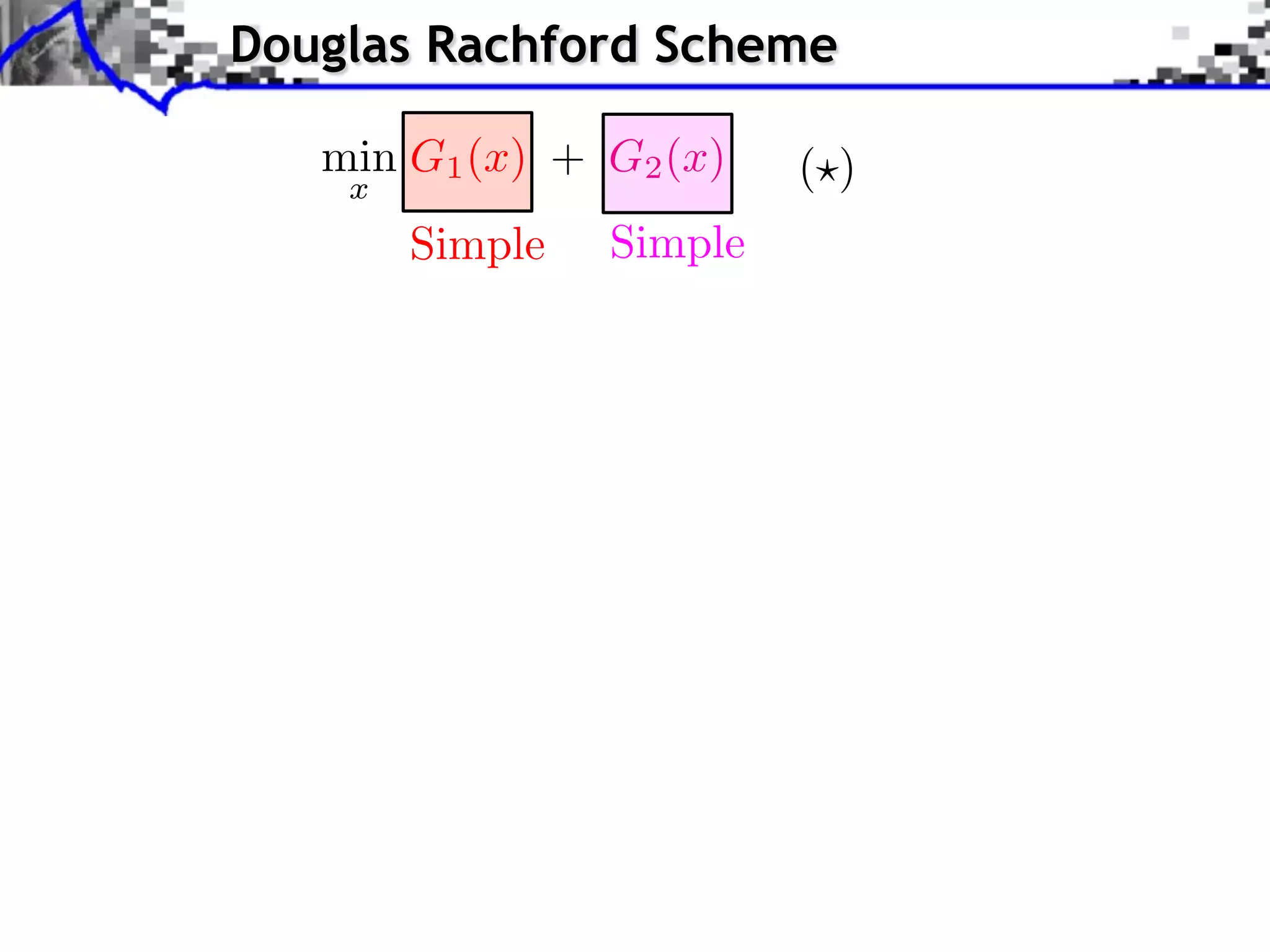
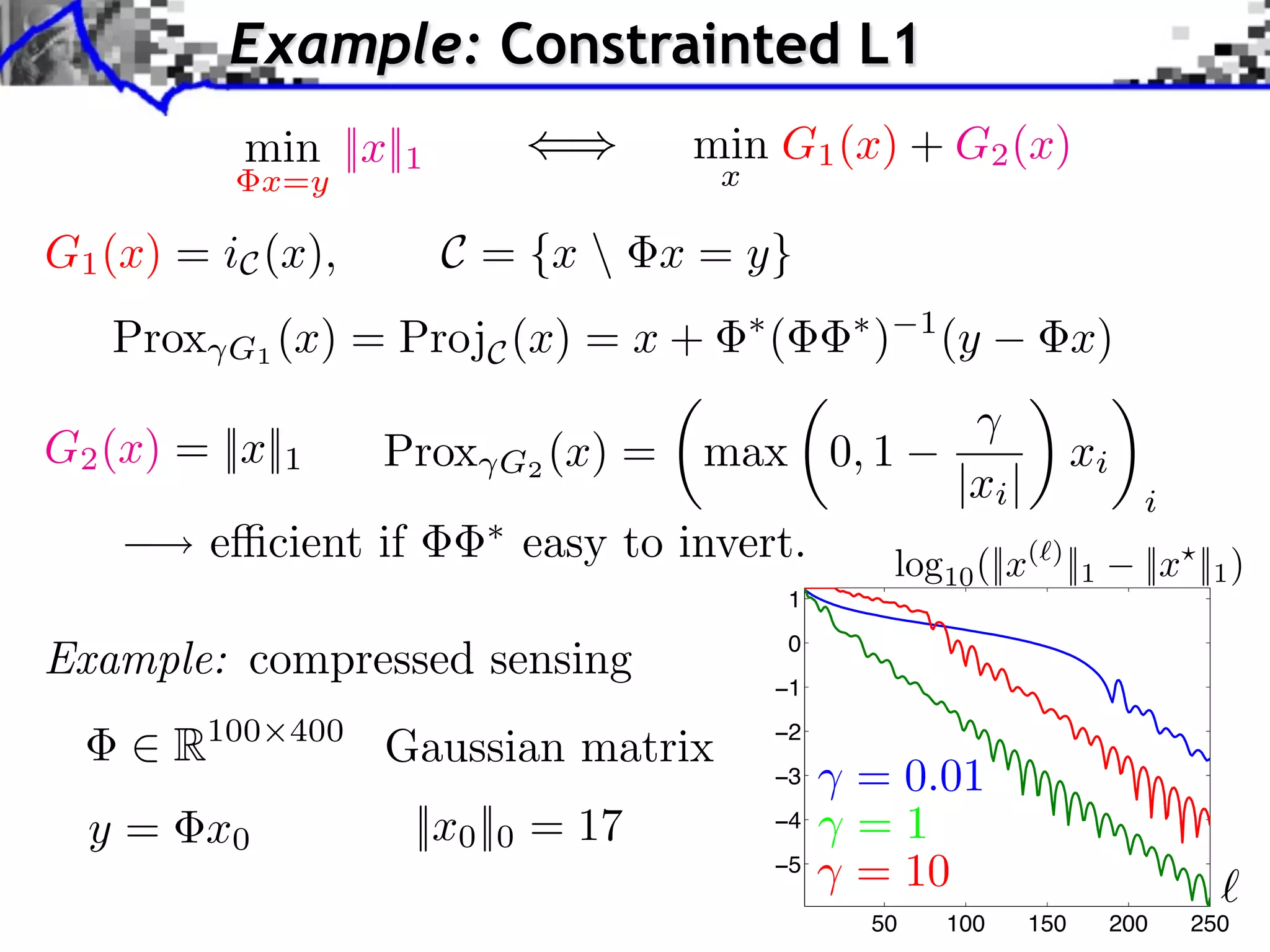
The document discusses proximal splitting methods for solving optimization problems with composite objectives. It begins by introducing inverse problems regularization and how proximal operators are used to solve problems by splitting them into smooth and non-smooth components. It then presents the forward-backward splitting method, Douglas-Rachford splitting, and the generalized forward-backward splitting method. Examples are provided to illustrate how these methods can be applied to problems like L1 regularization, constrained L1 minimization, and block sparsity regularization.

1. A Review of Proximal
Splitting Methods
with a new one
Hugo Raguet
Gabriel Peyré Jalal Fadili
www.numerical-tours.com

2. Overview
• Inverse Problems Regularization
• Proximal Splitting
• Generalized Forward-Backward

3. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input

4. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.

5. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.
Inpainting: set of missing pixels, P = Q | |.
0 if x ,
(Kf )(x) =
f (x) if x / .
K

6. Inverse Problems
Forward model: y = K f0 + w RP
Observations Operator (Unknown) Noise
: RQ RP Input
Denoising: K = IdQ , P = Q.
Inpainting: set of missing pixels, P = Q | |.
0 if x ,
(Kf )(x) =
f (x) if x / .
Super-resolution: Kf = (f k) , P = Q/ .
K K

7. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.

8. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity

9. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity
Choice of : tradeo
Noise level Regularity of f0
||w|| J(f0 )

10. Inverse Problem Regularization
Noisy measurements: y = Kf0 + w.
Prior model: J : RQ R assigns a score to images.
1
f argmin ||y Kf ||2 + J(f )
f RQ 2
Data fidelity Regularity
Choice of : tradeo
Noise level Regularity of f0
||w|| J(f0 )
No noise: 0+ , minimize f argmin J(f )
f RQ ,Kf =y

11. L1 Regularization
x0 RN
coe cients

12. L1 Regularization
x0 RN f0 = x0 RQ
coe cients image

13. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w

14. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w
= K ⇥ ⇥ RP N

15. L1 Regularization
x0 RN f0 = x0 RQ y = Kf0 + w RP
coe cients image observations
K
w
= K ⇥ ⇥ RP N
Sparse recovery: f = x where x solves
1
min ||y x||2 + ||x||1
x RN 2
Fidelity Regularization

16. Inpainting Problem
K 0 if x ,
(Kf )(x) =
f (x) if x / .
Measures: y = Kf0 + w

17. Overview
• Inverse Problems Regularization
• Proximal Splitting
• Generalized Forward-Backward

18. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x z||2 + G(z)
z 2

19. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x z||2 + G(z)
z 2
12 log(1 + x2 )
G(x) = ||x||1 = |xi | 10
|x| ||x||0
8
i
Prox G (x)i = max 0, 1
6
xi 4
|xi | 2
0
−2
G(x)
−10 −8 −6 −4 −2 0 2 4 6 8 10
10
8
6
4
2
0
−2
−4
−6
−8
ProxG (x)
−10
−10 −8 −6 −4 −2 0 2 4 6 8 10

20. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x z||2 + G(z)
z 2
12 log(1 + x2 )
G(x) = ||x||1 = |xi | 10
|x| ||x||0
8
i
Prox G (x)i = max 0, 1
6
xi 4
|xi | 2
0
G(x) = ||x||0 = | {i xi = 0} | −2
−10 −8 −6 −4 −2 0 2 4
G(x)
6 8 10
xi if |xi | 2 ,
10
Prox G (x)i =
8
0 otherwise.
6
4
2
0
−2
−4
−6
−8
ProxG (x)
−10
−10 −8 −6 −4 −2 0 2 4 6 8 10

21. Proximal Operators
Proximal operator of G:
1
Prox G (x) = argmin ||x z||2 + G(z)
z 2
12 log(1 + x2 )
G(x) = ||x||1 = |xi | 10
|x| ||x||0
8
i
Prox G (x)i = max 0, 1
6
xi 4
|xi | 2
0
G(x) = ||x||0 = | {i xi = 0} | −2
−10 −8 −6 −4 −2 0 2 4
G(x)
6 8 10
xi if |xi | 2 ,
10
Prox G (x)i =
8
0 otherwise.
6
4
2
0
G(x) = log(1 + |xi |2 ) −2
−4
i −6
3rd order polynomial root.
−8
ProxG (x)
−10
−10 −8 −6 −4 −2 0 2 4 6 8 10

22. Proximal Splitting Methods
Solve min E(x)
x H
Problem: Prox E is not available.

23. Proximal Splitting Methods
Solve min E(x)
x H
Problem: Prox E is not available.
Splitting: E(x) = F (x) + Gi (x)
i
Smooth Simple

24. Proximal Splitting Methods
Solve min E(x)
x H
Problem: Prox E is not available.
Splitting: E(x) = F (x) + Gi (x)
i
Smooth Simple
F (x)
Iterative algorithms using:
Prox Gi (x)
solves
Forward-Backward: F + G
Douglas-Rachford: Gi
Primal-Dual: G i Ai
Generalized FB: F+ Gi

25. Forward-Backward
min F (x) + G(x) ( )
x RN
Smooth Simple

26. Forward-Backward
min F (x) + G(x) ( )
x RN
Smooth Simple
Forward-backward: x( +1)
= Prox G x( )
F (x( ) )

27. Forward-Backward
min F (x) + G(x) ( )
x RN
Smooth Simple
Forward-backward: x( +1)
= Prox G x( )
F (x( ) )
Projected gradient descent: G= C

28. Forward-Backward
min F (x) + G(x) ( )
x RN
Smooth Simple
Forward-backward: x( +1)
= Prox G x( )
F (x( ) )
Projected gradient descent: G= C
Theorem: Let F be L-Lipschitz.
If < 2/L, x( )
x a solution of ( )

29. Forward-Backward
min F (x) + G(x) ( )
x RN
Smooth Simple
Forward-backward: x( +1)
= Prox G x( )
F (x( ) )
Projected gradient descent: G= C
Theorem: Let F be L-Lipschitz.
If < 2/L, x( )
x a solution of ( )
Multi-step accelerations (Nesterov, Beck-Teboule).

30. Example: L1 Regularization
1
min || x y||2 + ||x||1 min F (x) + G(x)
x 2 x
1
F (x) = || x y||2
2
F (x) = ( x y) L = || ||
G(x) = ||x||1
⇥
Prox G (x)i = max 0, 1 xi
|xi |
Forward-backward Iterative soft thresholding

31. Douglas Rachford Scheme
min G1 (x) + G2 (x) ( )
x
Simple Simple

32. Douglas Rachford Scheme
min G1 (x) + G2 (x) ( )
x
Simple Simple
Douglas-Rachford iterations:
z( +1)
= 1 z( ) + RProx G2 RProx G1 (z ( ) )
2 2
x( +1)
= Prox G2 (z ( +1) )
Reflexive prox:
RProx G (x) = 2Prox G (x) x

33. Douglas Rachford Scheme
min G1 (x) + G2 (x) ( )
x
Simple Simple
Douglas-Rachford iterations:
z( +1)
= 1 z( ) + RProx G2 RProx G1 (z ( ) )
2 2
x( +1)
= Prox G2 (z ( +1) )
Reflexive prox:
RProx G (x) = 2Prox G (x) x
Theorem: If 0 < < 2 and ⇥ > 0,
x( )
x a solution of ( )

34. Example: Constrainted L1
min ||x||1 min G1 (x) + G2 (x)
x=y x
G1 (x) = iC (x), C = {x x = y}
Prox G1 (x) = ProjC (x) = x +
⇥
( ⇥
) 1
(y x)
G2 (x) = ||x||1 Prox G2 (x) = max 0, 1 xi
|xi | i
e⇥cient if easy to invert.

35. Example: Constrainted L1
min ||x||1 min G1 (x) + G2 (x)
x=y x
G1 (x) = iC (x), C = {x x = y}
Prox G1 (x) = ProjC (x) = x +
⇥
( ⇥
) 1
(y x)
G2 (x) = ||x||1 Prox G2 (x) = max 0, 1 xi
|xi | i
e⇥cient if easy to invert. log10 (||x( ) ||1 ||x ||1 )
1
Example: compressed sensing −1
0
R100 400
Gaussian matrix −2
−3 = 0.01
y = x0 ||x0 ||0 = 17 −4 =1
−5
= 10
50 100 150 200 250

36. Overview
• Inverse Problems Regularization
• Proximal Splitting
• Generalized Forward-Backward

37. GFB Splitting
n
min F (x) + Gi (x) ( )
x RN
i=1
Smooth Simple

38. GFB Splitting
n
min F (x) + Gi (x) ( )
x RN
i=1
Smooth Simple
i = 1, . . . , n,
( +1) ( ) ( )
zi = zi + Proxn Gi (2x
( )
zi F (x( ) )) x( )
n
1 ( +1)
x ( +1)
= zi
n i=1

39. GFB Splitting
n
min F (x) + Gi (x) ( )
x RN
i=1
Smooth Simple
i = 1, . . . , n,
( +1) ( ) ( )
zi = zi + Proxn Gi (2x
( )
zi F (x( ) )) x( )
n
1 ( +1)
x ( +1)
= zi
n i=1
Theorem: Let F be L-Lipschitz.
If < 2/L, x( )
x a solution of ( )
n=1 Forward-backward.
F =0 Douglas-Rachford.

40. Block Regularization
1 2
block sparsity: G(x) = ||x[b] ||, ||x[b] ||2 = x2
m
b B m b
iments Towards More Complex Penalization
(2) Bk
2
+ ` 1 `2
4
k=1 x 1,2
b B1 i b xi
⇥ x⇥⇥1 = i ⇥xi ⇥ b B i b xi2 +
i b xi
N: 256
b B2
b B
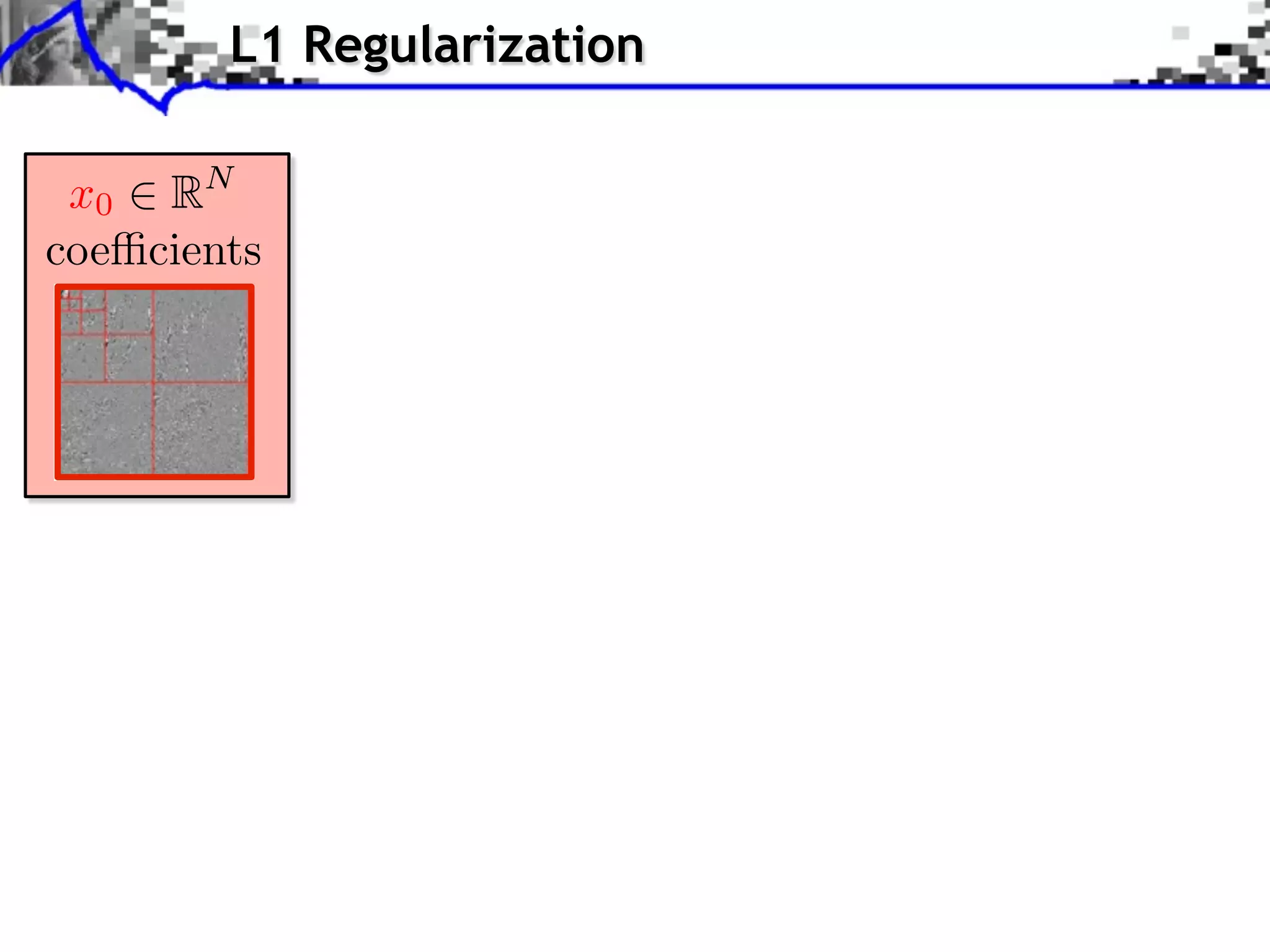
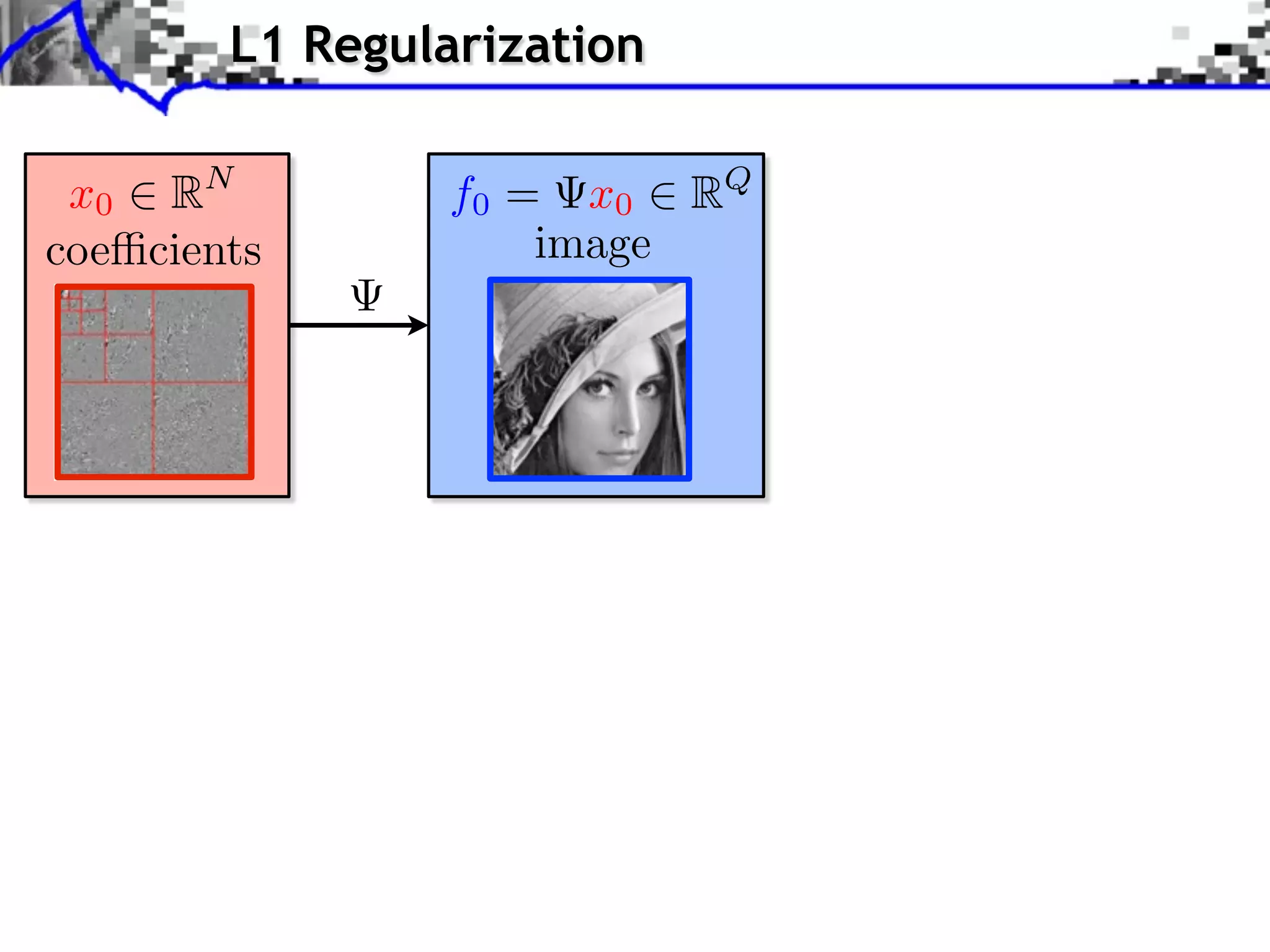
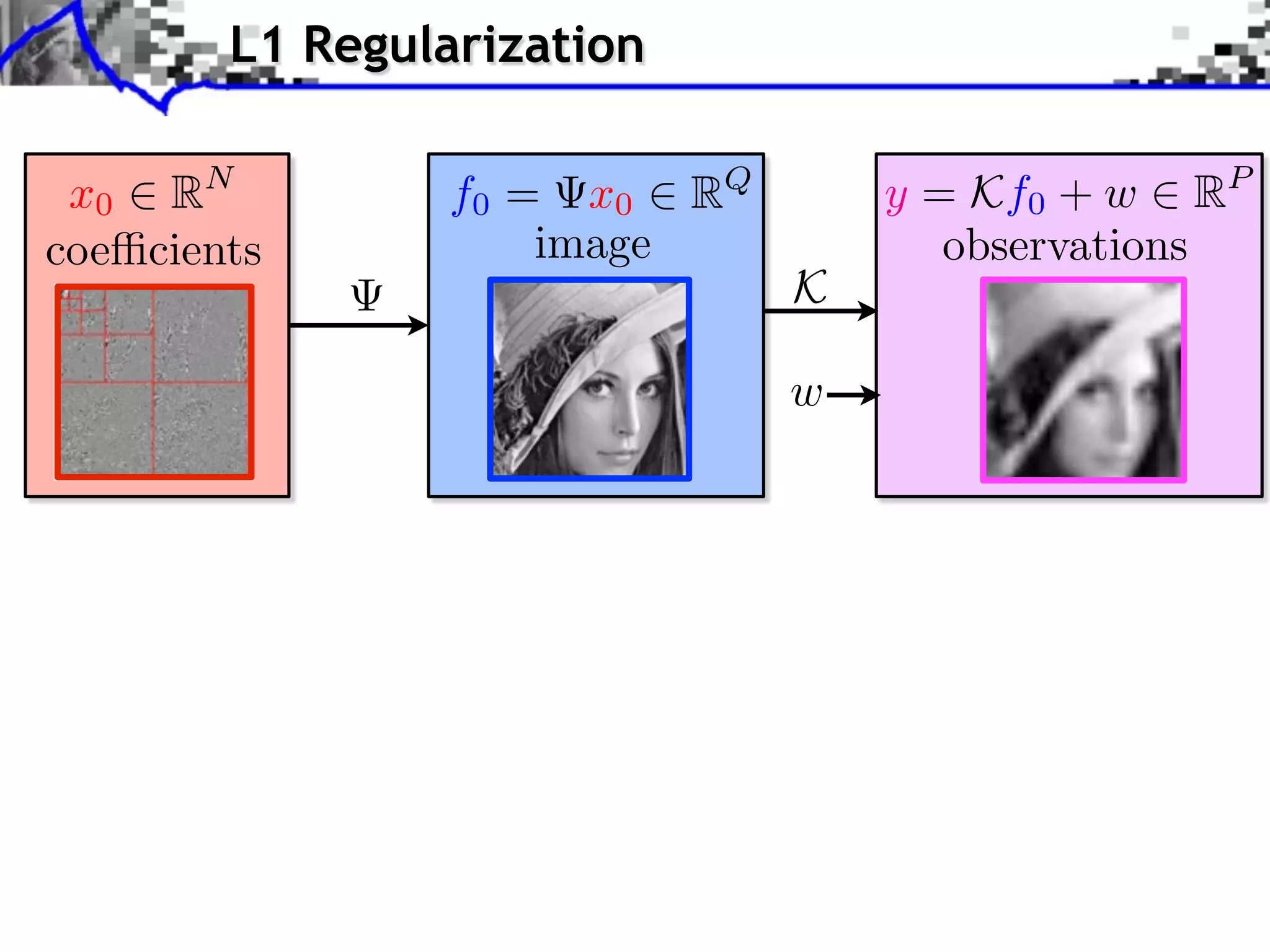
Image f = x Coe cients x.

41. Block Regularization
1 2
block sparsity: G(x) = ||x[b] ||, ||x[b] ||2 = x2
m
b B m b
iments Towards More Complex Penalization
Non-overlapping decomposition: B = B ... B
Towards More Complex Penalization
Towards More Complex Penalization
n
1 n
2 G(x) =4 x iBk
(2)
+ ` ` k=1 G 1,2
(x) Gi (x) = ||x[b] ||,
1 2 i=1 b Bi
b b 1b1 B1 i b xiixb xi
22
BB
⇥ x⇥x⇥x⇥⇥1 =i ⇥x⇥x⇥xi ⇥
⇥= ++ +
i b i
⇥ ⇥1 ⇥1 = i i ⇥i i ⇥ bb B B i
Bb xii2bi2xi2
bbx
i
N: 256
b b 2b2 B2 i
BB xi2 b2xi
b b xi
i
b B
Image f = x Coe cients x. Blocks B1 B1 B2

42. Block Regularization
1 2
block sparsity: G(x) = ||x[b] ||, ||x[b] ||2 = x2
m
b B m b
iments Towards More Complex Penalization
Non-overlapping decomposition: B = B ... B
Towards More Complex Penalization
Towards More Complex Penalization
n
1 n
2 G(x) =4 x iBk
(2)
+ ` ` k=1 G 1,2
(x) Gi (x) = ||x[b] ||,
1 2 i=1 b Bi
Each Gi is simple: b b 1b1 B1 i b xiixb xi
BB
22
⇥ x⇥x⇥x⇥⇥1 =i ⇥xG ⇥xi ⇥ m = b B B i b xii2bi2xi2
⇥ ⇥1 = i ⇥i i x +
i b i
⇤ m ⇥ b ⇥ Bi , ⇥ ⇥1Prox i ⇥xi ⇥(x) b max i0, 1
= Bb bx ++m
N: 256 ||x[b]b||B xi2 b2xi
2 2 B2
b B b i b b xi
i
b B
Image f = x Coe cients x. Blocks B1 B1 B2

43. Deconv. + Inpaint. 2min+CP Y ⇥ P K x CP Y + P 1 K2
Deconv. x 2Inpaint. min 2 ⇥ ` `
x x
k=1 x+1,2` k=1
log10(E−E
2 1 `2
Numerical Illustration
log10(E−
1 1
0
tmin
1 t : 298s; t :: 283s; t : 298s; t : 368s
0
−1 EFB ||y −1 ⇥x||368s PR
: 283s; PR tEFB 2 +
CP GCP(x)
i = TI wavelets
x 102
3
20 30 10 40
EFB
iteration 3
#
20
i
30 40
Numerical Experiments
iteration # EFB
log10(E−Emin)
log10(E−Emin)
PR
2 (2)
PR
Deconvolution minx 2 Y ⇥
= convolution 1.30e−03; 2 +λl1/l2: 1.30e−03; x
= inpainting+convolution `1 `2 4 1CP 2
CP
2 2
l1/l2
:K x λ
k=1
1 noise: 0.025; convol.: it. #50; SNR: 22.49dB #50; SNR: 22.49dB
noise: 0.025; convol.: 2
1
2 it.

0 0



tEFB: 161s; tPR: 173s; tCP: 190s N: 256
 10 20 30 10 40 20 30 40

iteration # iteration #
 EFB
log10(E−Emin)
3 PR 4
λ :
CP l1/l2
1.00e−03; λ4 : 1.00e−03;
 l1/l2
2
noise: 0.025;
 
degrad.: 0.4; 0.025; degrad.: 0.4; convol.: 2
 noise:

convol.: 2 it. #50; SNR: 21.80dB #50; SNR: 21.80dB
it.
1

 0

 
−1
 10 20
iteration #
30 40 x0

 λ2 : 1.30e−03;
l1/l2
log10 (E(x )
 
( )

E(x ))
y = x0 + w
  noise: 0.025; convol.: 2
x it. #50; SNR: 22.49dB

44. Conclusion
Inverse problems in imaging:
Large scale, N 106 .
Non-smooth (sparsity, TV, . . . )
(Sometimes) convex.
Highly structured (separability, p
norms, . . . ).

45. Conclusion
Inverse problems in imaging:
Large scale, N 106 .
Towards More Complex Penalization
Non-smooth (sparsity, TV, . . . )
(Sometimes) convex. b B1 i b xi
2
⇥ x⇥⇥1 = i ⇥xi ⇥ b B
2
i p xi +
Highly structured (separability, b
norms, . . . ).
b B2 i b xi2
Proximal splitting:
Unravel the structure of problems.
Parallelizable.
Decomposition G = k Gk

46. Conclusion
Inverse problems in imaging:
Large scale, N 106 .
Towards More Complex Penalization
Non-smooth (sparsity, TV, . . . )
(Sometimes) convex. b B1 i b xi
2
⇥ x⇥⇥1 = i ⇥xi ⇥ b B
2
i p xi +
Highly structured (separability, b
norms, . . . ).
b B2 i b xi2
Proximal splitting:
Unravel the structure of problems.
Parallelizable.
Open problems:
Decomposition G = k Gk
Less structured problems without smoothness.
Non-convex optimization.