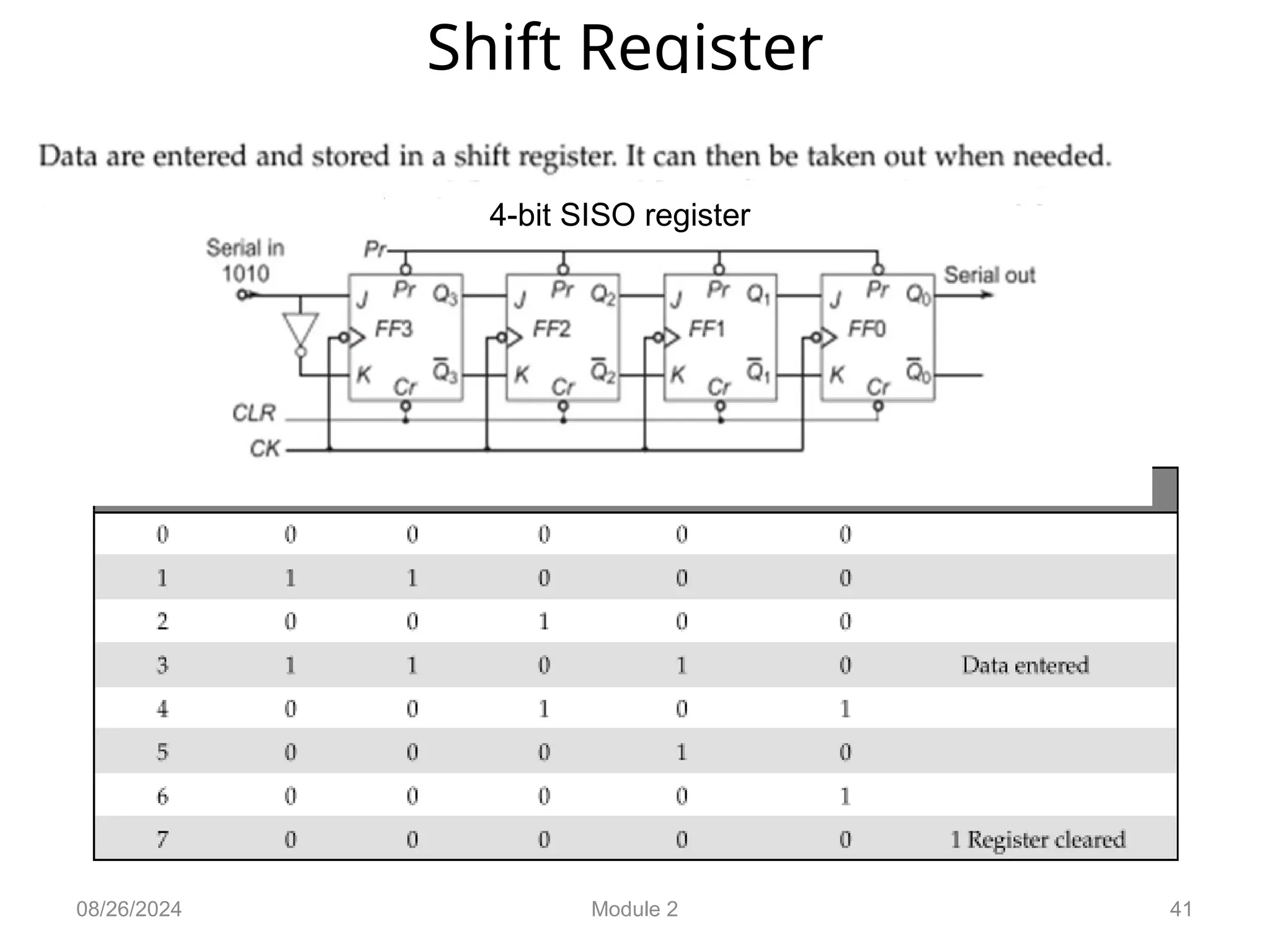
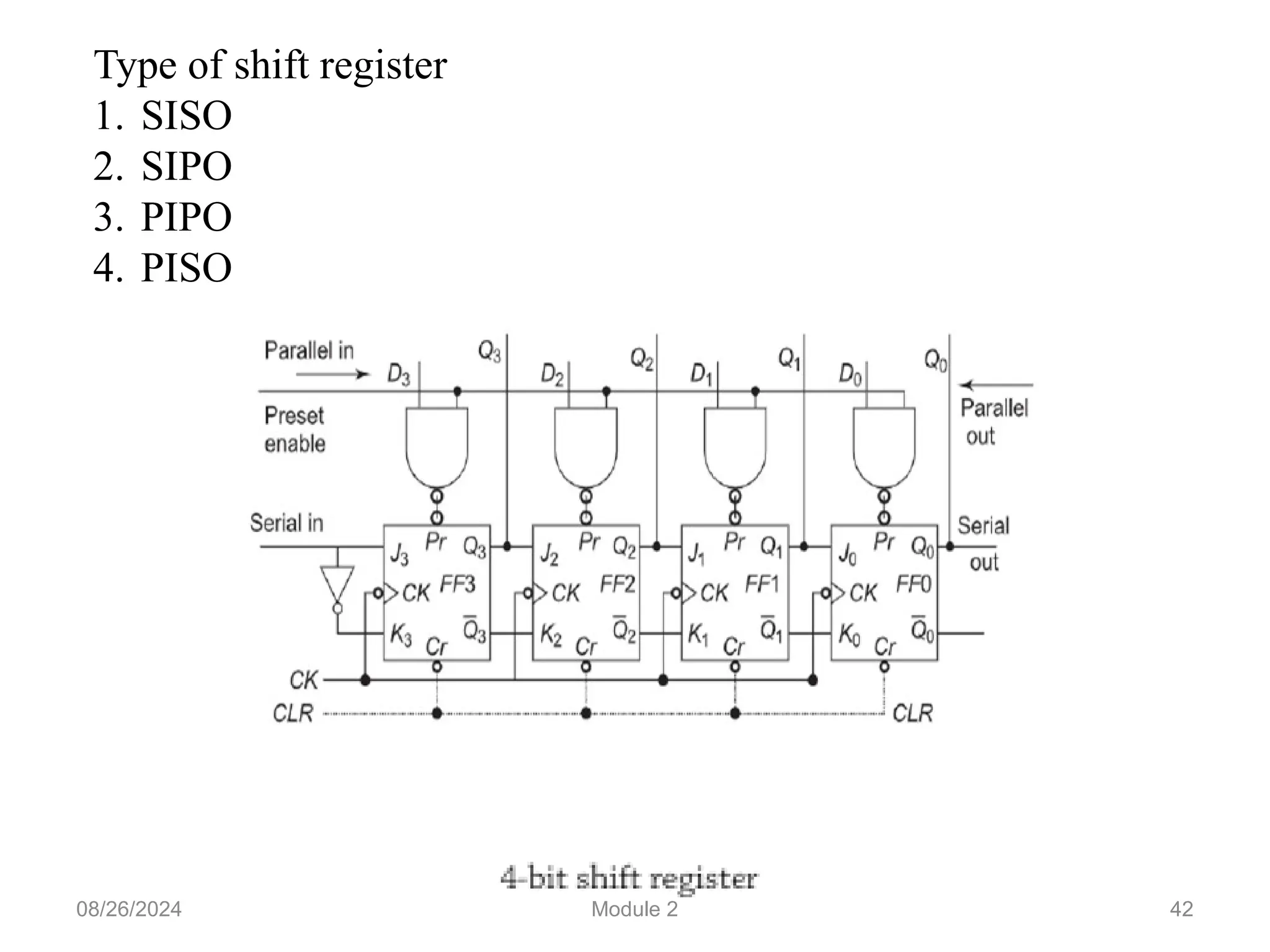
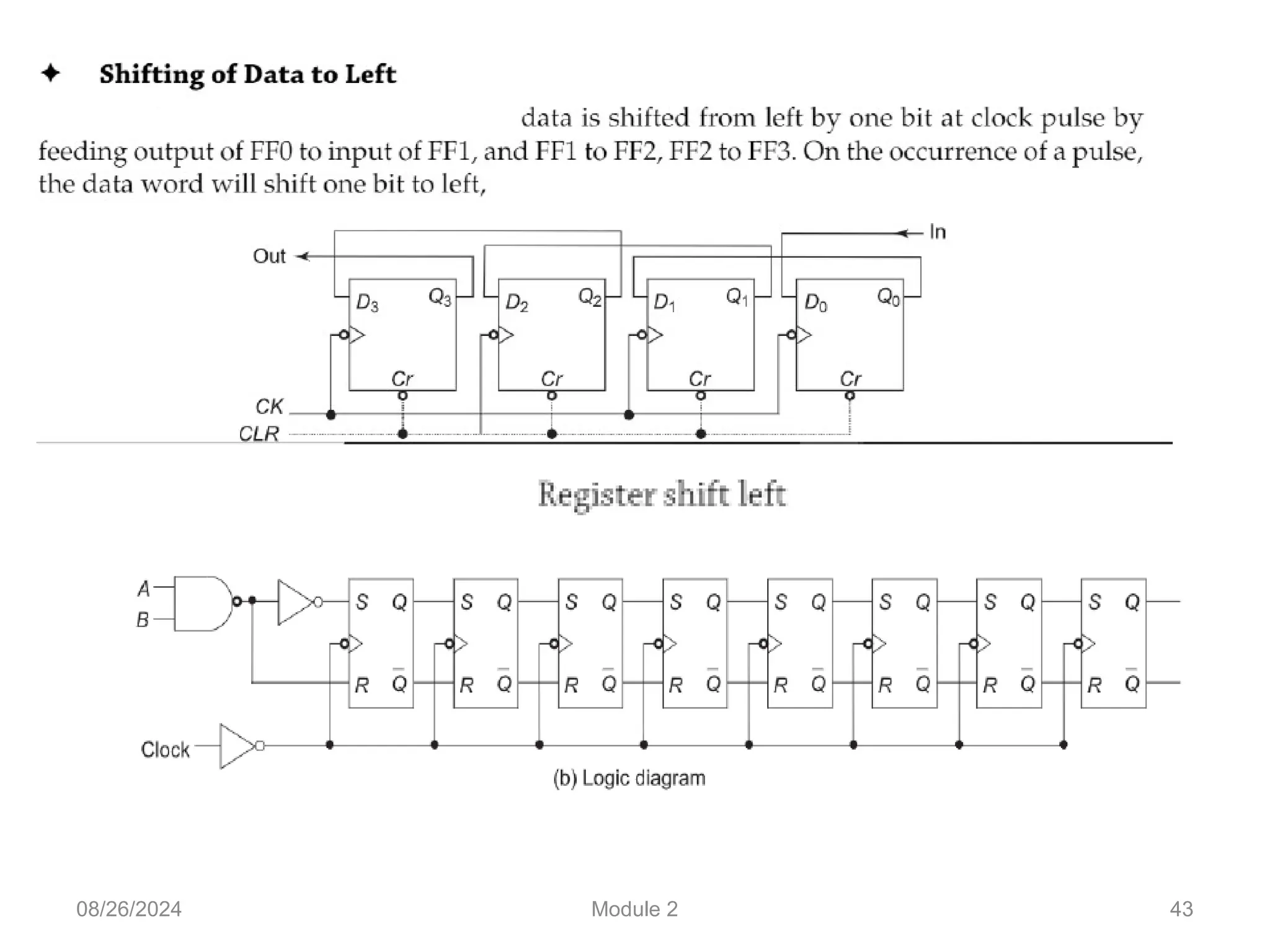
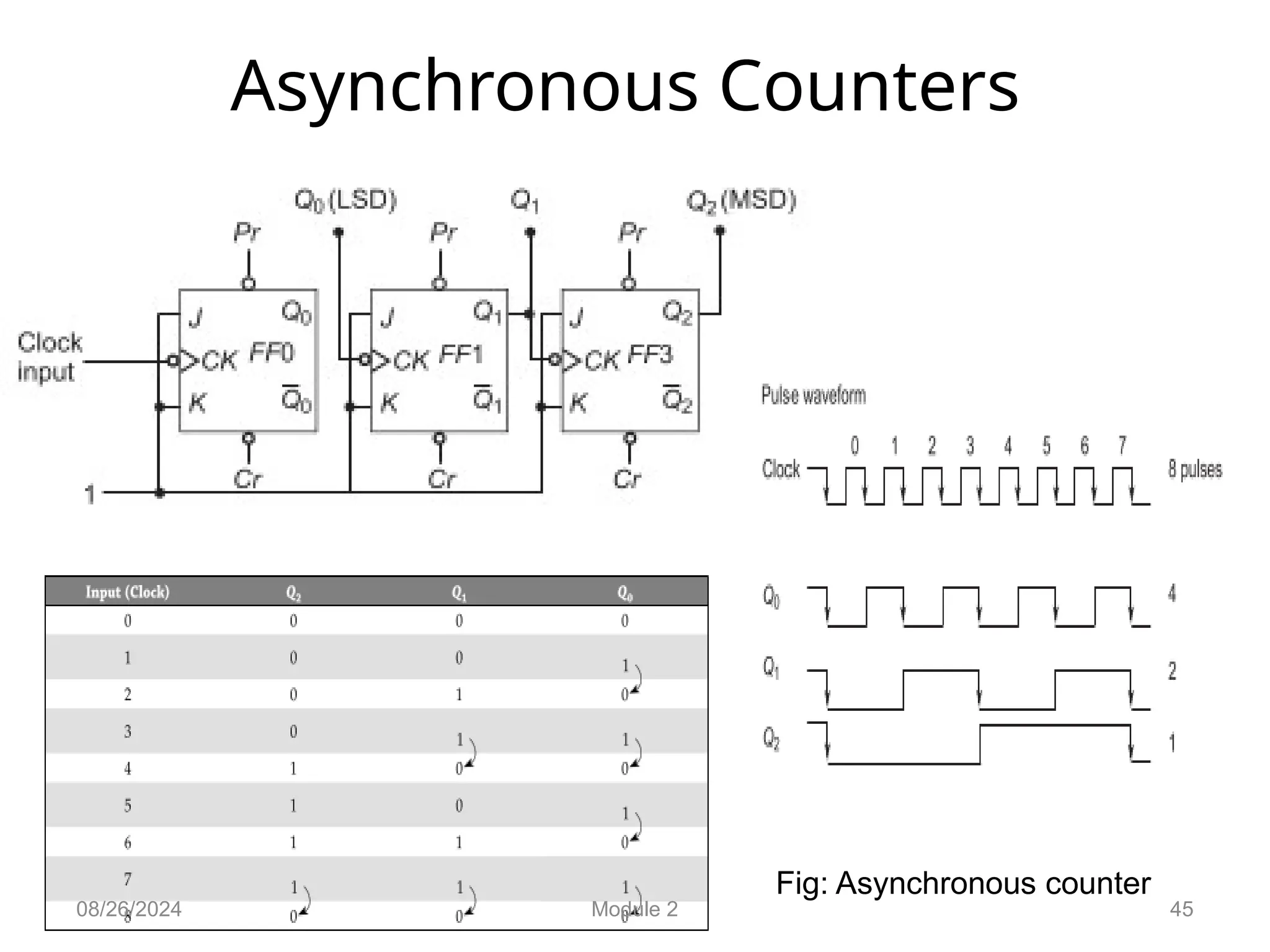
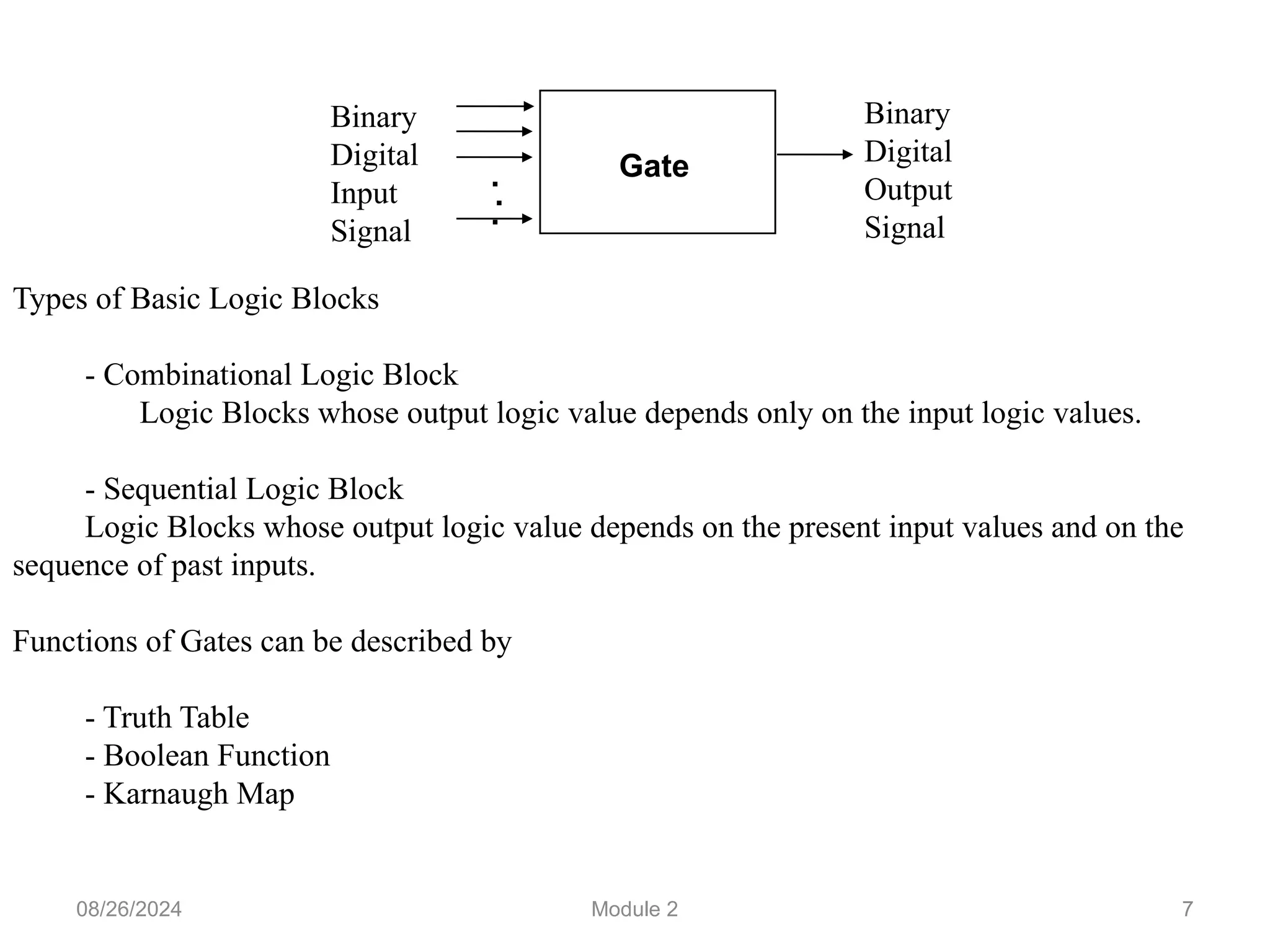
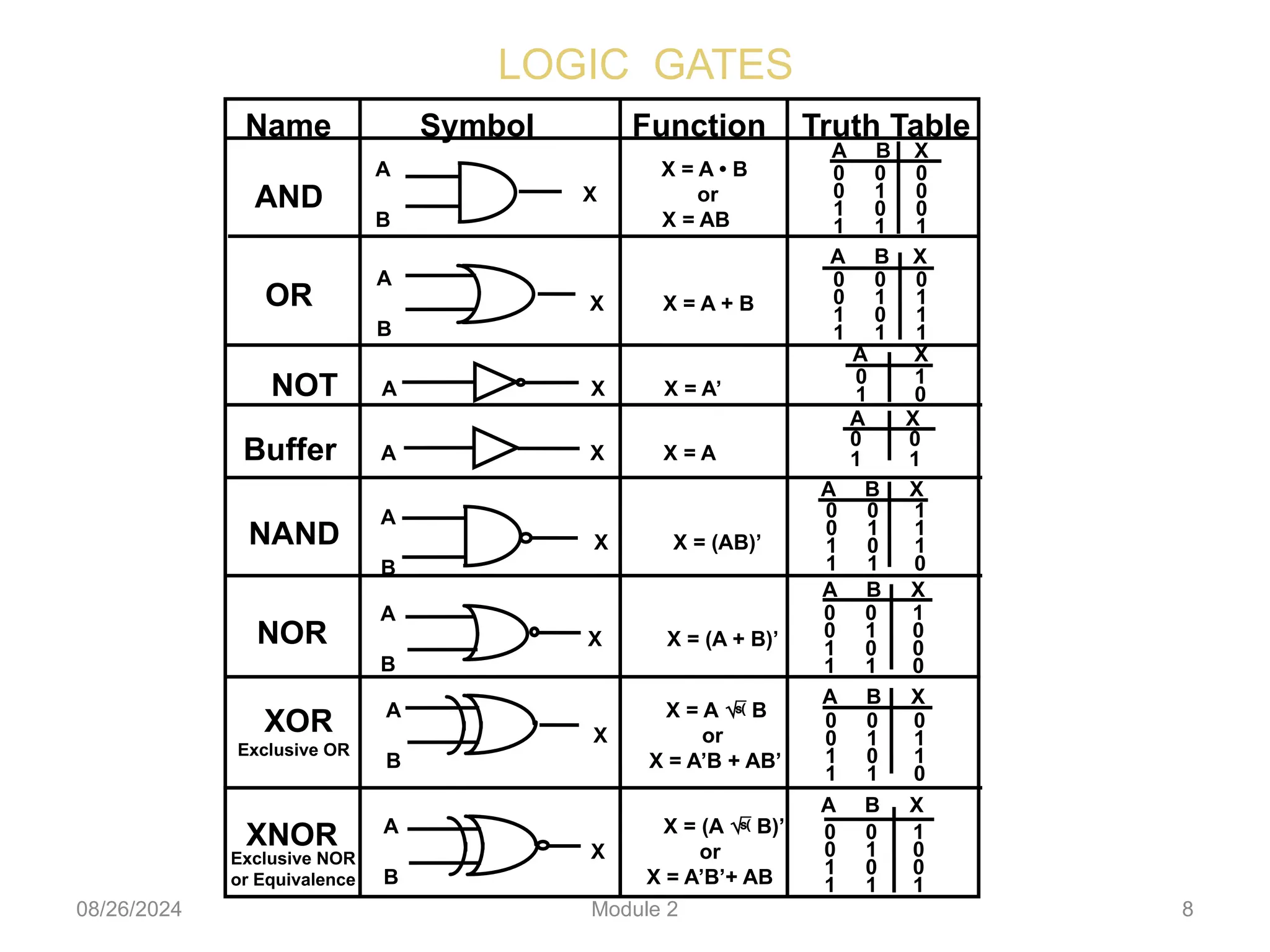
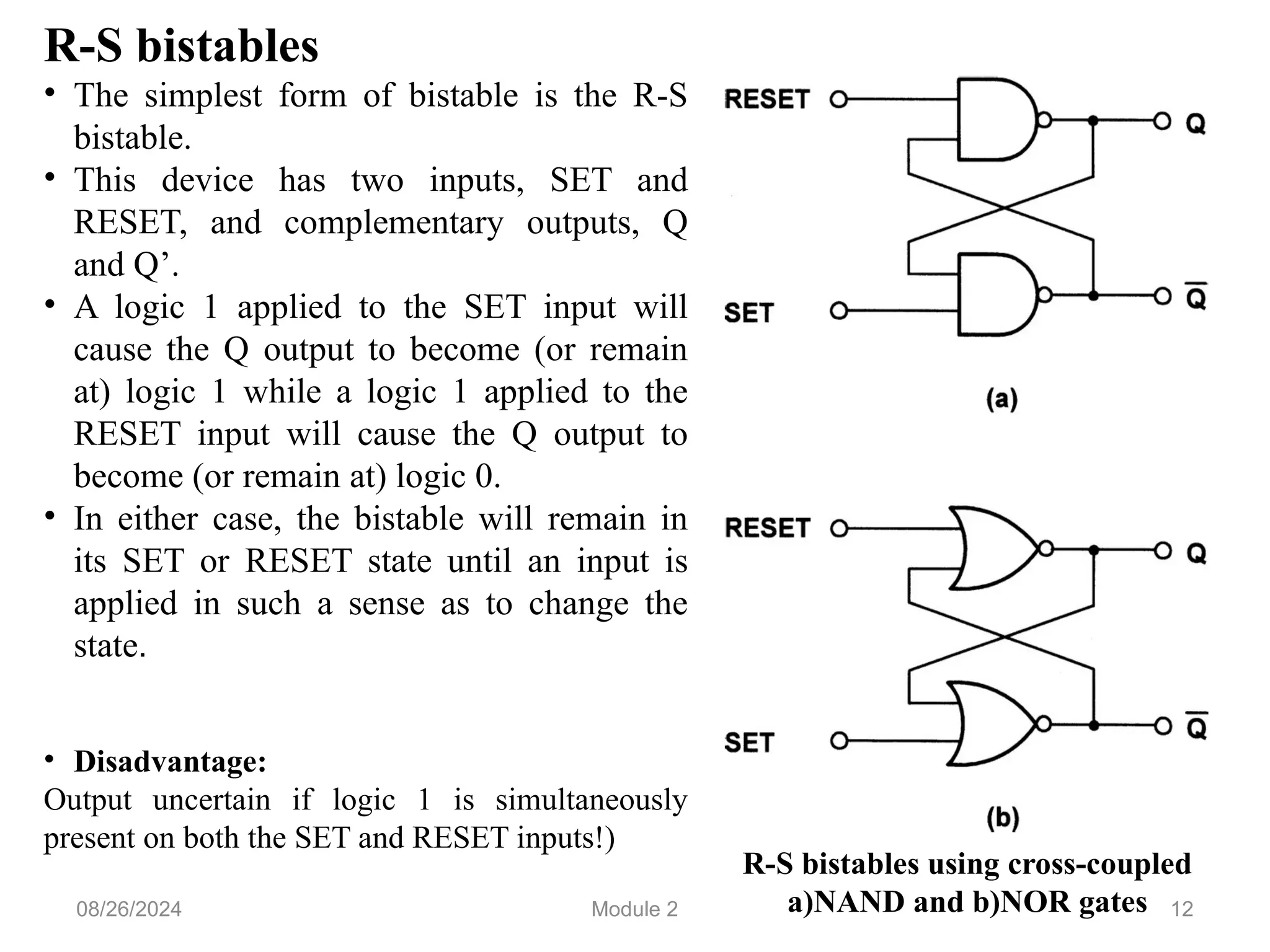
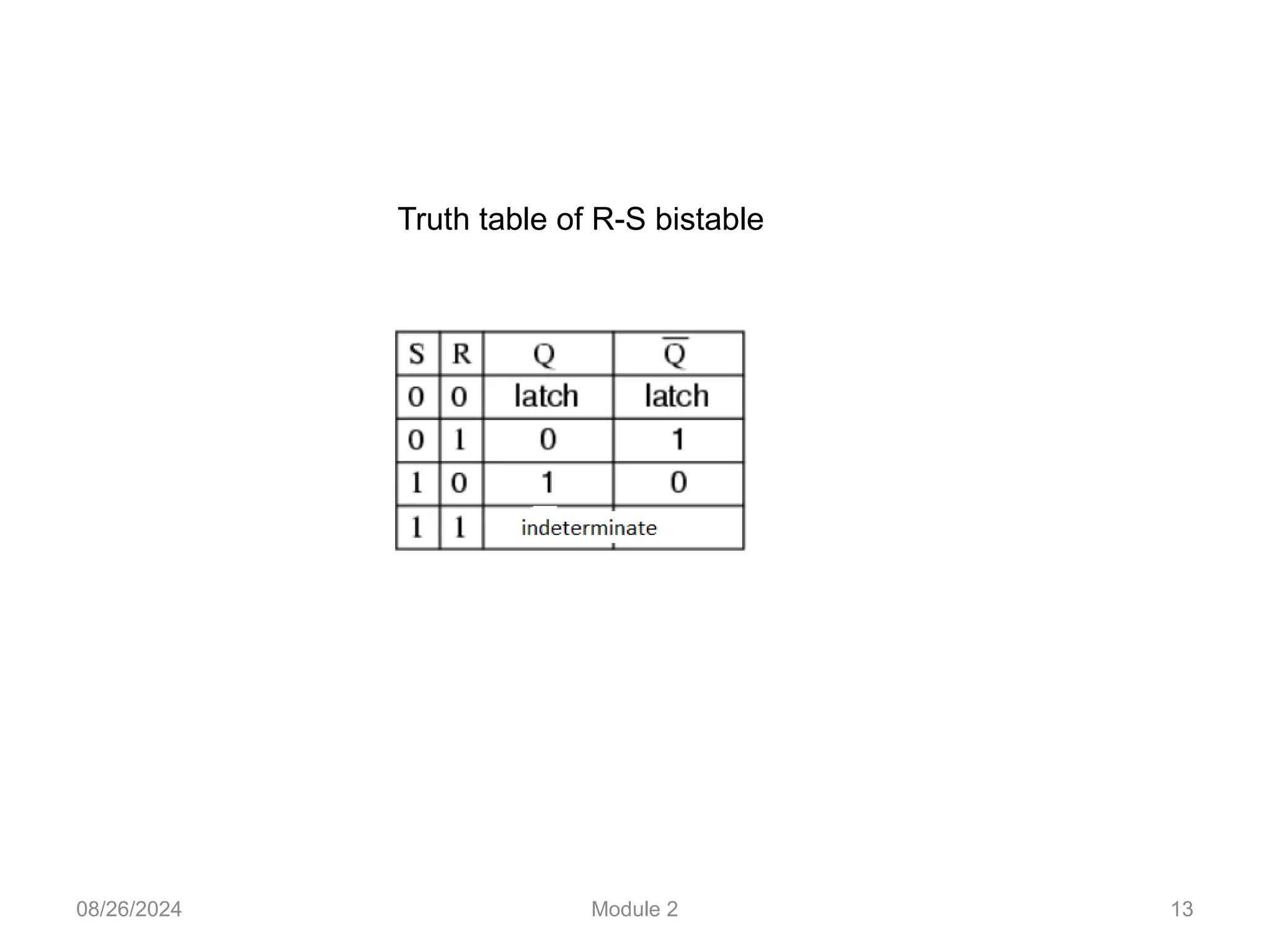
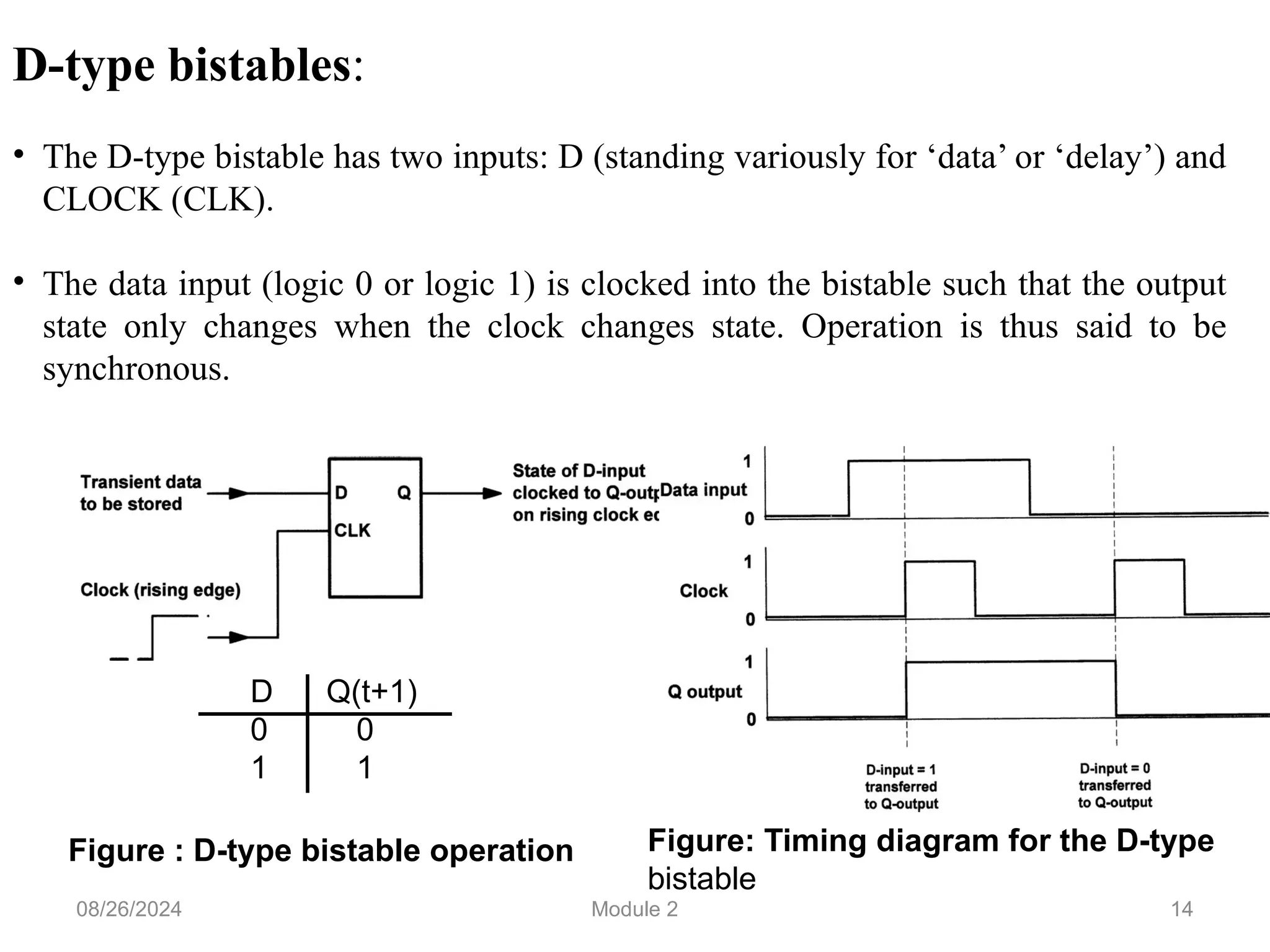
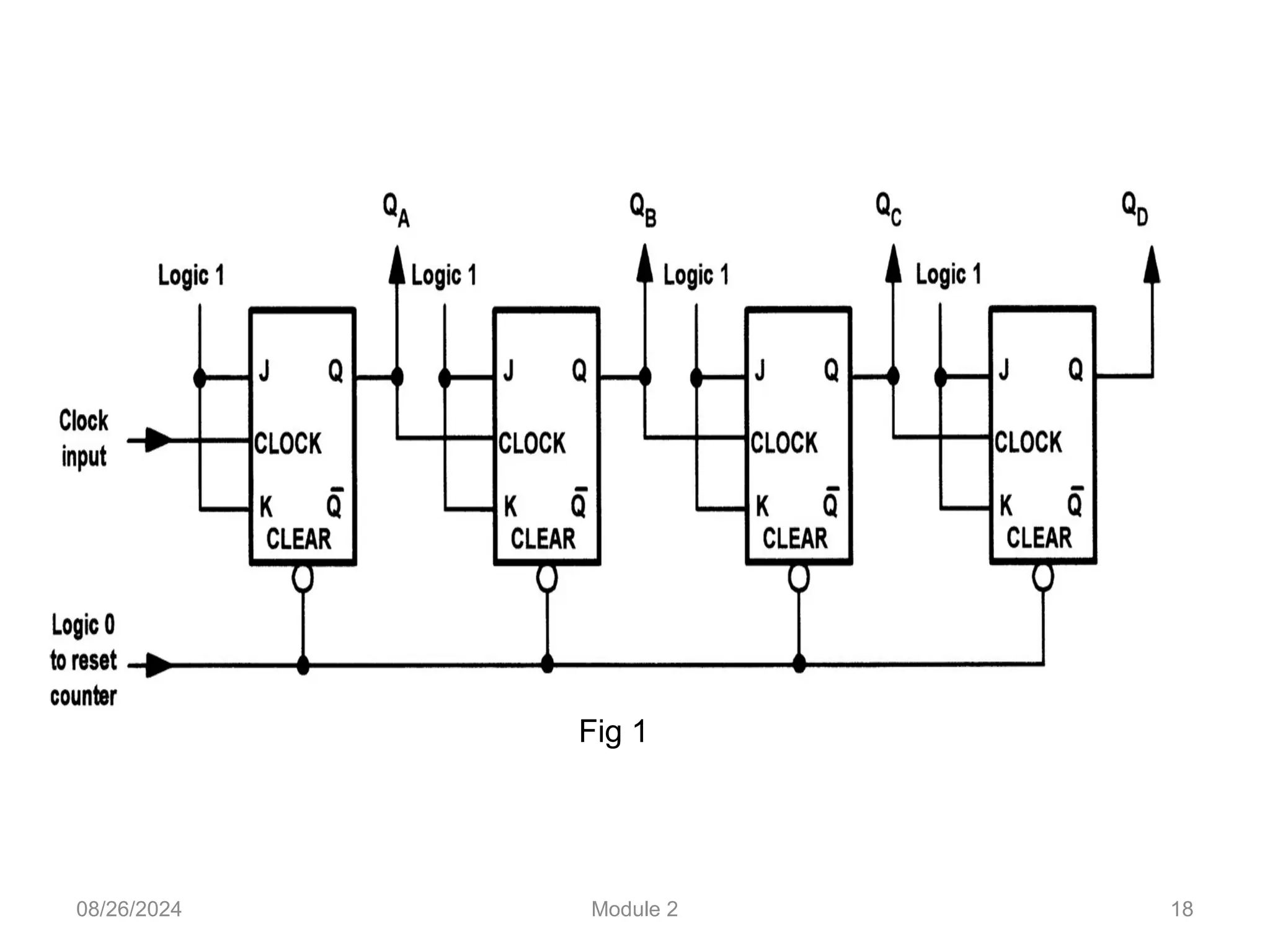
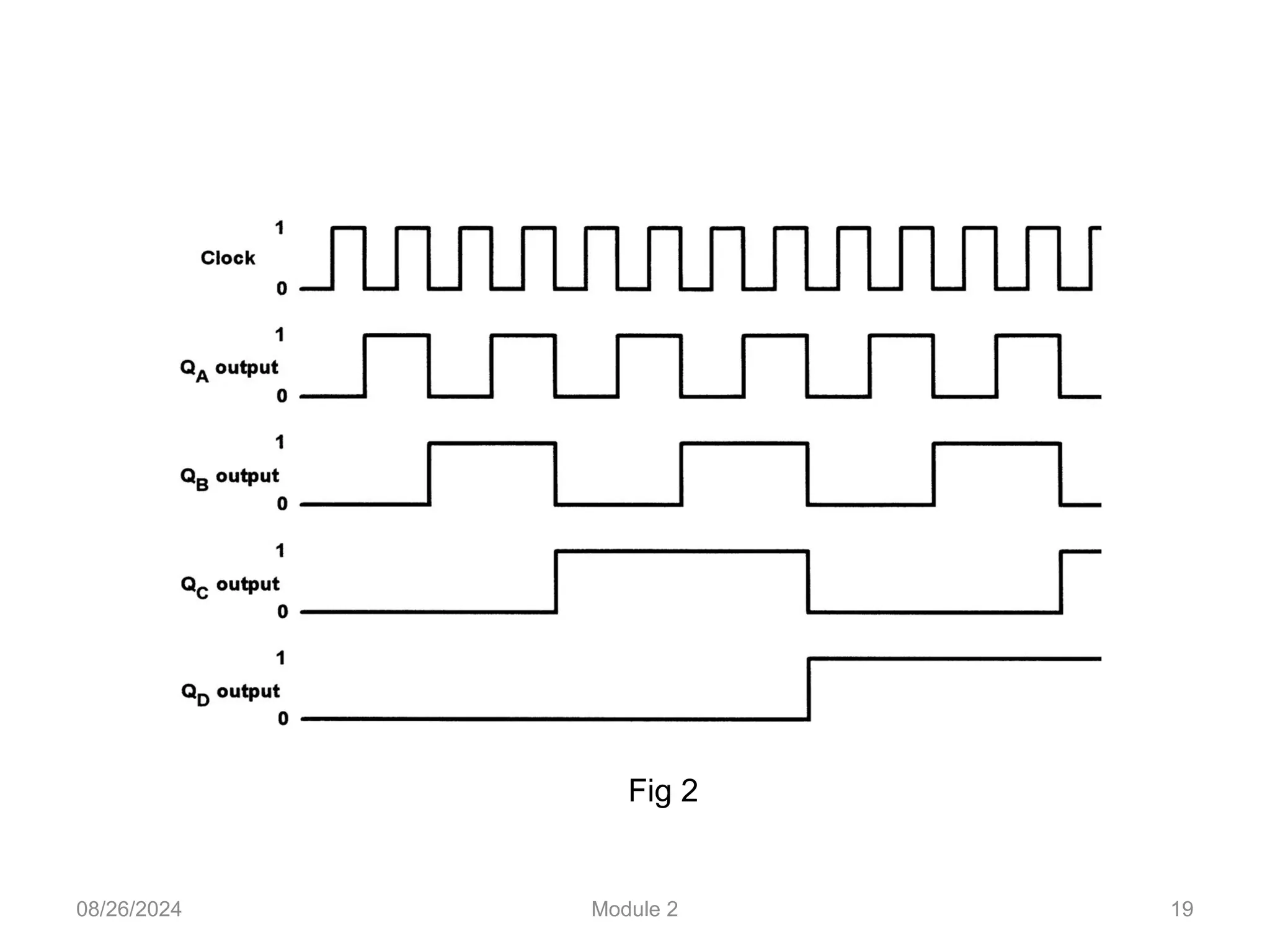
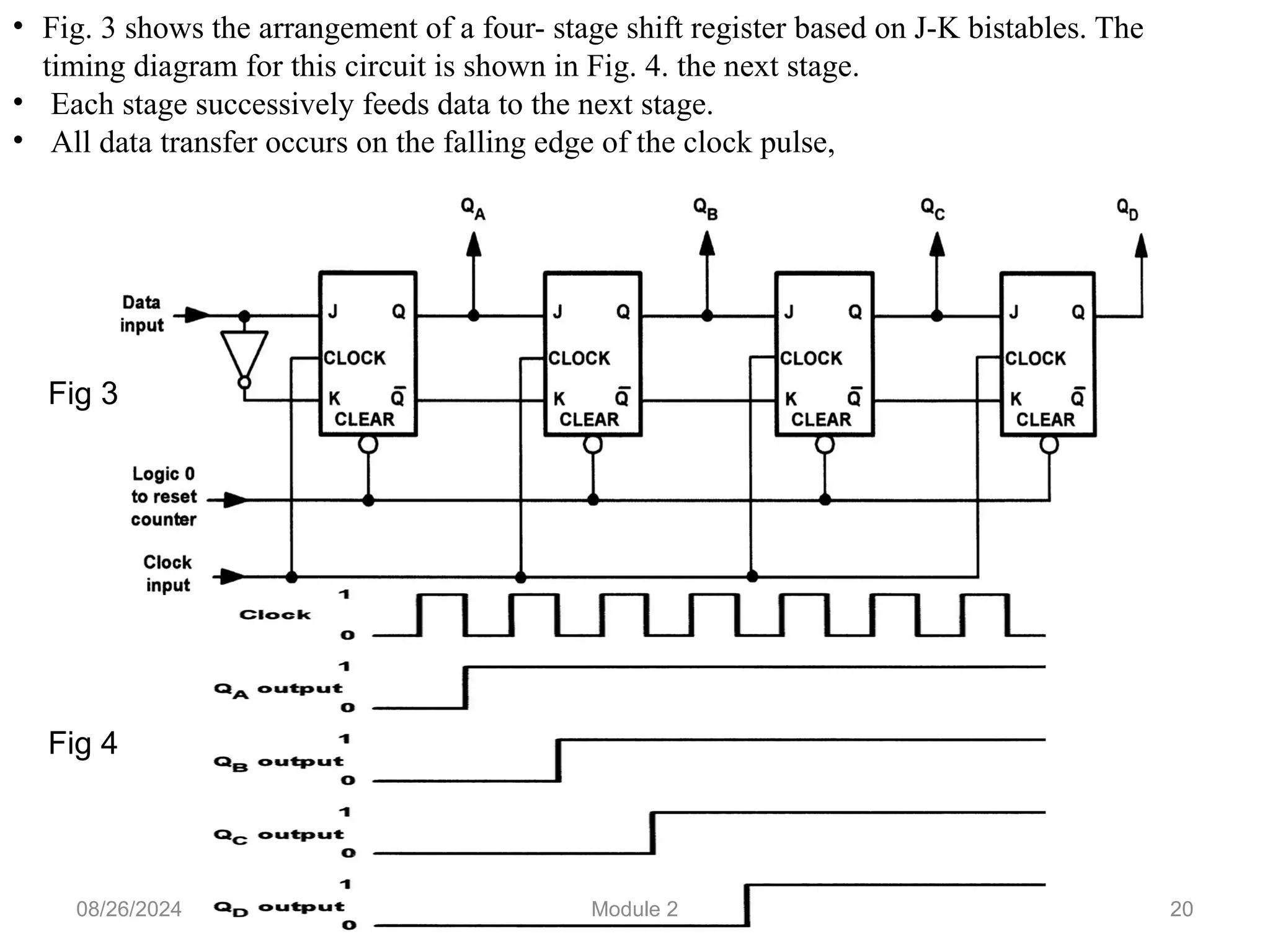
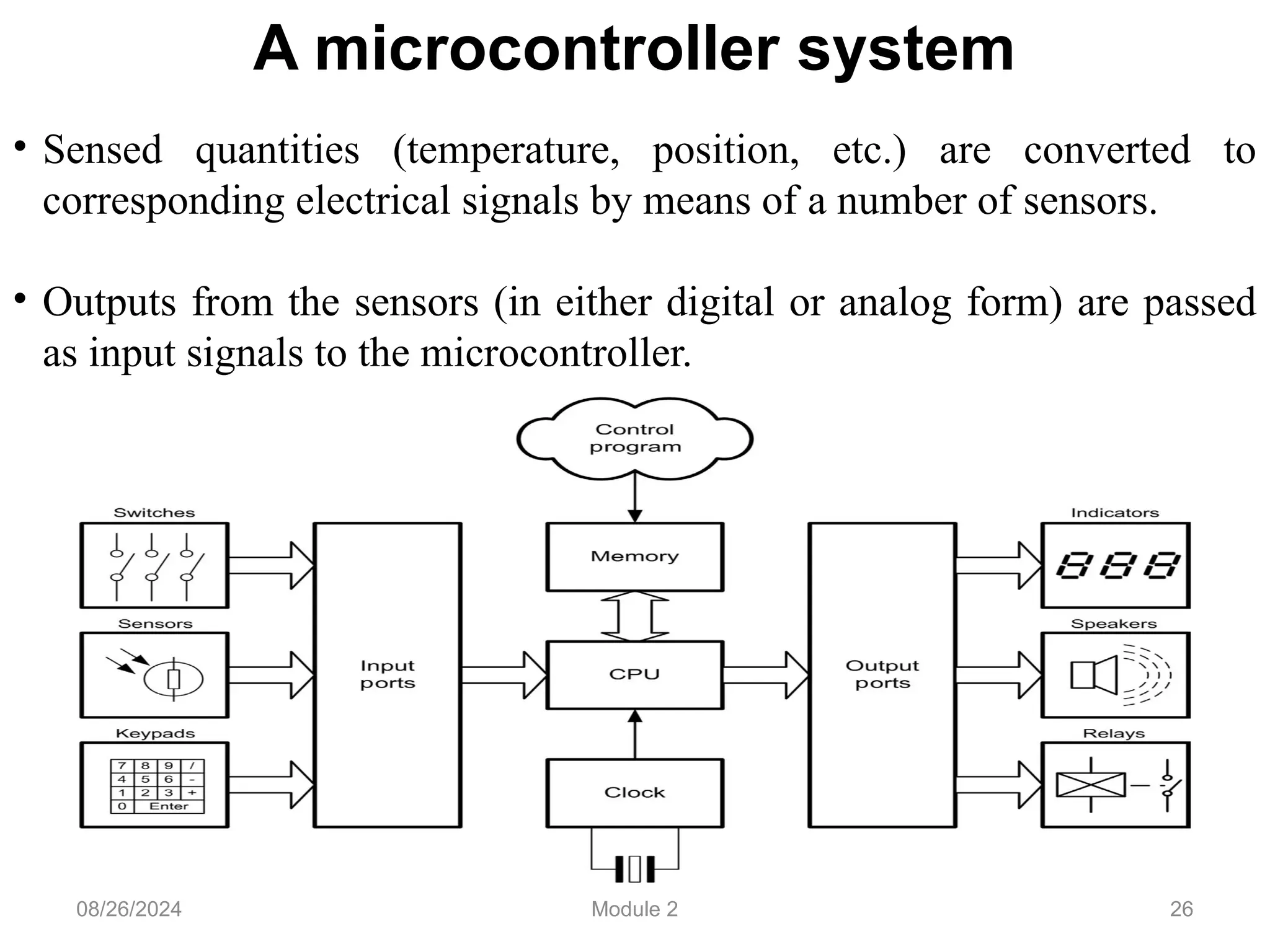
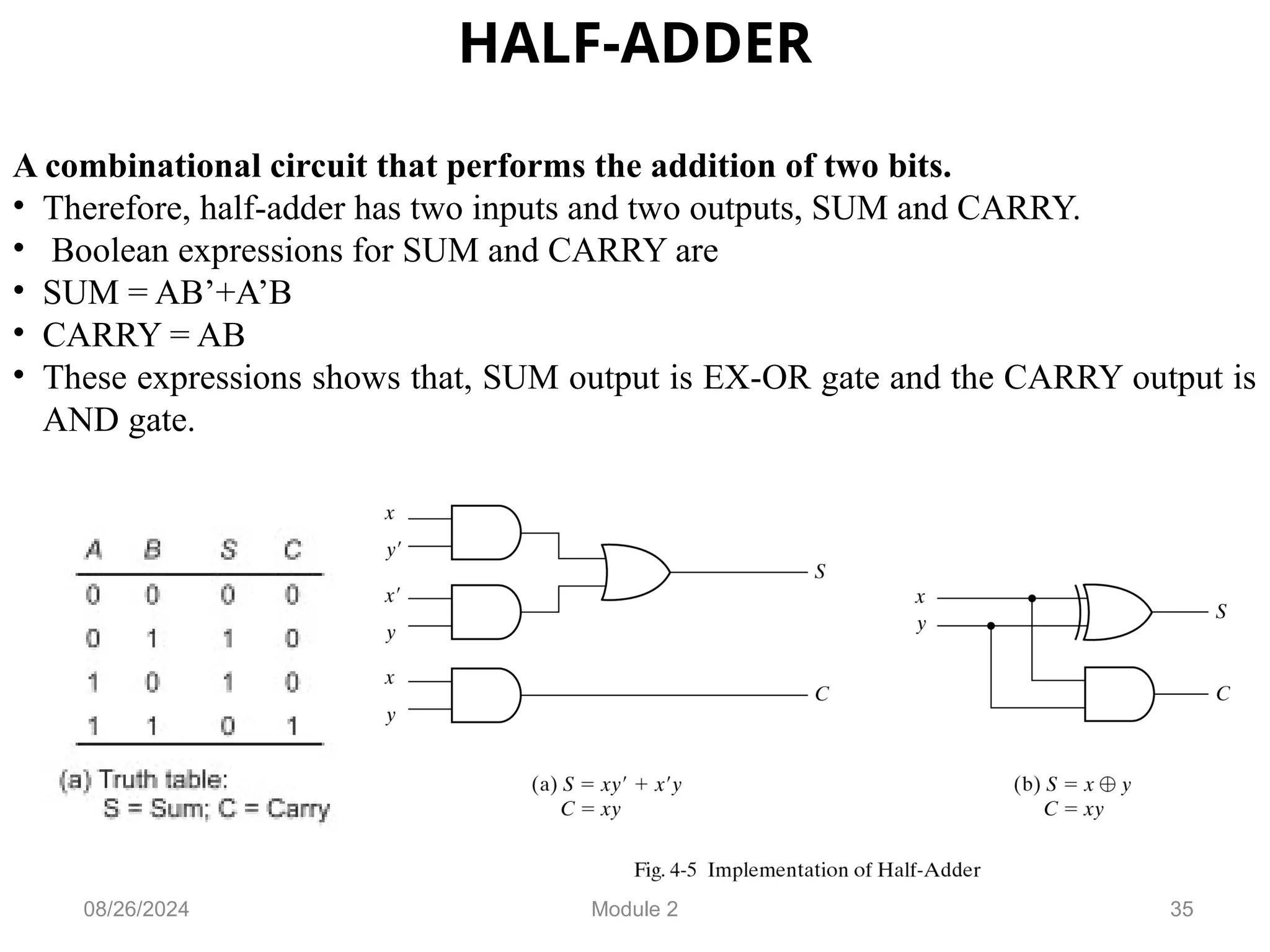
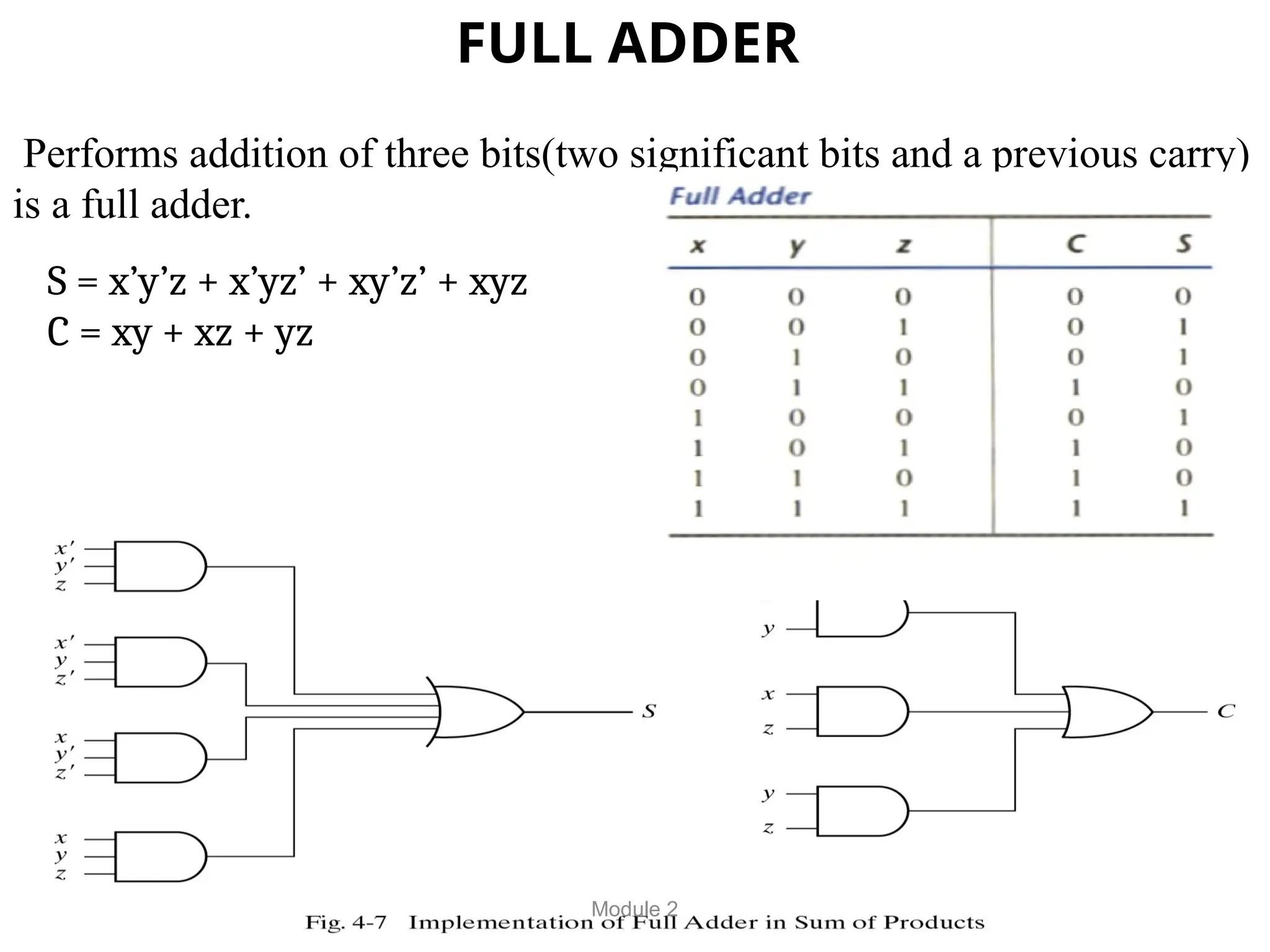
The document outlines the syllabus for a basic electronics course covering modules on electronic circuits, logic circuits, and embedded systems. It details fundamental concepts such as logic gates, bistables, and microcontroller operations, as well as design examples for various logic circuits and their applications. Additionally, it provides information on data representation, input/output devices, and components like multiplexers and decoders.

1. Basic Electronics -21ELN14/24

2. Syllabus
• Module1
Electronic Circuits : Power supplies ,Amplifiers, Operational
Amplifiers ,Oscillators .
• Module2
Logic Circuits
• Module3
Embedded Systems , Sensors and Interfacing , Communication Interface.
• Module 4
Analog and Digital Communication
• Module5
Cellular wireless networks ,wireless network topologies, Satellite
communication ,Optical fiber communication ,Microwave communication
2
08/26/2024 Module 2

3. Text Books
3
Text 1 Text 2
08/26/2024 Module 2

4. Text Books
4
Text 3 Text 4
08/26/2024 Module 2

5. Module 2
Logic Circuits –
Logic gates, Bistables, R-S Bistables, D-type Bistables, J-K Bistables. Text 1:
Chapter 10
Data representation, Data types, Data storage, A microcontroller system. Text 1:
Chapter 11
Realization using basic gates and truth table the Half Adder (Text 4: Fig.11.11) and
Full Adder (Text 4: Table 11.5 & Fig. 11.13), Multiplexer (Text 4: 10.5.3) and
decoder (Text 4: 10.5.4).
Shift registers, Register type – operation and truth table (Text 4: 13.2, 13.3),
Counters and asynchronous counters (Text 4: 13.5, 13.6)
Text 4: Fig. 11.11, Fig. 11.13, 10.5.3, 10.5.4, 13.2, 13.3, 13.5, 13.6
(No simplification of Boolean algebra, no K-maps. Only logic circuit, working
and truth table)

6. Logic Gates
• Logic gates are circuits designed to produce the
basic logic functions, AND, OR, etc.
• These circuits are designed to be interconnected into
larger, more complex, logic circuit arrangements.
• Form the basic building blocks of all digital systems
6
08/26/2024 Module 2

7. 7
Types of Basic Logic Blocks
- Combinational Logic Block
Logic Blocks whose output logic value depends only on the input logic values.
- Sequential Logic Block
Logic Blocks whose output logic value depends on the present input values and on the
sequence of past inputs.
Functions of Gates can be described by
- Truth Table
- Boolean Function
- Karnaugh Map
Gate
.
.
.
Binary
Digital
Input
Signal
Binary
Digital
Output
Signal
08/26/2024 Module 2

8. 8
LOGIC GATES
A
X X = (A + B)’
B
Name Symbol Function Truth Table
AND
A X = A • B
X or
B X = AB
0 0 0
0 1 0
1 0 0
1 1 1
0 0 0
0 1 1
1 0 1
1 1 1
OR
A
X X = A + B
B
NOT A X X = A’
0 1
1 0
Buffer A X X = A
A X
0 0
1 1
NAND
A
X X = (AB)’
B
0 0 1
0 1 1
1 0 1
1 1 0
NOR
0 0 1
0 1 0
1 0 0
1 1 0
XOR
Exclusive OR
A X = A  B
X or
B X = A’B + AB’
0 0 0
0 1 1
1 0 1
1 1 0
A X = (A  B)’
X or
B X = A’B’+ AB
XNOR
Exclusive NOR
or Equivalence
A B X
A B X
A X
A B X
A B X
A B X
A B X
0 0 1
0 1 0
1 0 0
1 1 1
08/26/2024 Module 2

9. 9
Combinational logic
By using a standard range of logic levels (i.e. voltage levels
used to represent the logic 1 and logic 0 states) logic circuits
can be combined in order to solve complex logic functions.
Example 1
A logic circuit is to be constructed
that will produce a logic 1 output
whenever two or more of its three
inputs are at logic 1.
08/26/2024 Module 2

10. 10
Example 2:
A committee of three individuals decide issues for an
organization. Each individual votes either yes or no for each
proposal that arises. A proposal is passed if it receives at least
two yes votes. Design a circuit that determines whether a
proposal passes.
Example 3:
Show how an arrangement of basic logic gates (AND, OR and
NOT) can be used to produce the exclusive-OR function.
08/26/2024 Module 2

11. 11
Bistables
• The output of a bistable has two stable states (logic 0 or logic 1)
and, once set in one of these states, the device will remain at a
particular logic level for an indefinite period until reset.
• Similar to ‘memory cell’ because it will remain in its latched
state (whether set or reset) until a signal is applied to it in order
to change its state.
08/26/2024 Module 2

12. 12
R-S bistables
• The simplest form of bistable is the R-S
bistable.
• This device has two inputs, SET and
RESET, and complementary outputs, Q
and Q’.
• A logic 1 applied to the SET input will
cause the Q output to become (or remain
at) logic 1 while a logic 1 applied to the
RESET input will cause the Q output to
become (or remain at) logic 0.
• In either case, the bistable will remain in
its SET or RESET state until an input is
applied in such a sense as to change the
state.
• Disadvantage:
Output uncertain if logic 1 is simultaneously
present on both the SET and RESET inputs!)
R-S bistables using cross-coupled
a)NAND and b)NOR gates
08/26/2024 Module 2

13. 08/26/2024 Module 2 13
Truth table of R-S bistable

14. 14
D-type bistables:
• The D-type bistable has two inputs: D (standing variously for ‘data’ or ‘delay’) and
CLOCK (CLK).
• The data input (logic 0 or logic 1) is clocked into the bistable such that the output
state only changes when the clock changes state. Operation is thus said to be
synchronous.
Figure : D-type bistable operation Figure: Timing diagram for the D-type
bistable
D Q(t+1)
0 0
1 1
08/26/2024 Module 2

15. 15
D-type bistables:
• Additional subsidiary inputs (usuallyactive low) are provided
which can be used to directly set or reset the bistable. These are
usually called PRESET (PR) and CLEAR (CLR).
• D-type bistables are used both as latches (a simple form of
memory) and as binary dividers.
08/26/2024 Module 2

16. 16
J-K bistables
• J-K bistables have two clocked inputs (J and K), two direct inputs (PRESET and
CLEAR), a CLOCK (CK) input, and outputs (Q and Q’).
• As with R-S bistables, the two outputs are complementary (i.e. when one is 0 the
other is 1, and vice versa).
• Similarly, the PRESET and CLEAR inputs are both active low (i.e. a 0 on the
PRESET input will set the Q output to 1 whereas a 0 on the CLEAR input will set
the Q output to 0).
Truth table
08/26/2024 Module 2

17. 17
• J-K bistables can be configured in various ways including
binary dividers, shift registers and latches
Fig. 1 shows the arrangement of a four-stage binary counter
based on J-K bistables. The timing diagram for this circuit
is shown in Fig. 2.
Each stage successively divides the clock input signal by a
factor of two.
Logic 1 input is transferred to the respective Q-output on the
falling edge of the clock pulse and all J and K inputs must be
taken to logic 1 to enable binary Counting.
08/26/2024 Module 2

18. 18
08/26/2024 Module 2
Fig 1

19. 08/26/2024 Module 2 19
Fig 2

20. 20
• Fig. 3 shows the arrangement of a four- stage shift register based on J-K bistables. The
timing diagram for this circuit is shown in Fig. 4. the next stage.
• Each stage successively feeds data to the next stage.
• All data transfer occurs on the falling edge of the clock pulse,
Fig 3
Fig 4
08/26/2024 Module 2

21. 21
Question:
A logic arrangement has to be designed so that it produces the pulse train shown in
Fig.6. Devise a logic circuit arrangement that will generate this pulse train from a
regular square wave input.
Solution
A two-stage binary divider (based on J-K bistables) can be used together with a two-
input AND gate as shown in Fig. 5. The waveforms for this logic arrangement are
shown in Fig. 7
Fig 6
Fig 5
Fig 7
08/26/2024 Module 2

22. 22
Data representation
• Binary numbers – particularly large
ones – not convenient to handle.
• So binary numbers converted to
decimal (base 10) and hexadecimal
(base 16).
• The first 16 numbers in binary, denary
and hexadecimal are shown in Table 1.
A single hexadecimal character (in the
range zero to F) is used to represent a
group of four binary digits (bits).
Table 1
08/26/2024 Module 2

23. 23
Data representation
• Group of four bits (or single hex
character) is sometimes called a nibble.
• A byte of data comprises a group of
eight bits.
• Thus a byte can be represented by just
two hexadecimal (hex) characters.
• A group of 16 bits (a word) can be
represented by four hex characters.
• 32 bits (a double word) by eight hex
characters.
• A $ symbol or H before the number
denotes hexadecimal.
• For example, 64 means decimal ‘sixty-
four’; whereas $64 means hexadecimal
‘six-four’
Table 1
08/26/2024 Module 2

24. 08/26/2024 Module 2 24
Questions:
• Convert hexadecimal A3
into binary.
• Convert binary 11101000
binary to hexadecimal.

25. 25
Data types
• A byte of data can be stored at each address within the total memory space of a
microprocessor system. Hence one byte can be stored at each of the 65,536 memory
locations within a microprocessor system having a 16-bit address bus.
• Individual bits within a byte are numbered from 0 (least significant bit) to 7 (most
significant bit). In the case of 16-bit words, the bits are numbered from 0 (least
significant bit) to 15 (most significant bit).
• Negative (or signed) numbers can be represented using two’s complement notation
where the leading (most significant) bit indicates the sign of the number (1 =
negative, 0 = positive).
08/26/2024 Module 2
• For example, the signed 8-bit
number 10000001 represents the
denary number −1. The range of
integer data values that can be
represented as bytes, words and
long words are shown in below
Table

26. 26
A microcontroller system
• Sensed quantities (temperature, position, etc.) are converted to
corresponding electrical signals by means of a number of sensors.
• Outputs from the sensors (in either digital or analog form) are passed
as input signals to the microcontroller.
08/26/2024 Module 2

27. 27
• Operation of the microcontroller is controlled by a sequence of
software instructions known as a control program.
• Control program operates continuously, examining inputs from
sensors, user settings and time data before making changes to the
output signals sent to one or more controlled devices.
• The microcontroller also accepts inputs from the user.
08/26/2024 Module 2

28. 28
• Controlled quantities are produced by the controlled devices in
response to output signals from the microcontroller.
• Microcontroller must produce a specific state on each of the lines
connected to its output ports in response to a particular combination of
states present on each of the lines connected to its input ports .
• Microcontrollers must also have a central processing unit (CPU)
capable of performing simple arithmetic, logical and timing operations
08/26/2024 Module 2

29. 29
Input devices
• Input devices supply information to the computer system from the
outside world.
• Example: keyboard, mouse, scanner etc.
• In microcontrollers: sensors, switches, proximity detectors etc.
• Must provide logically compatible signal to the input of
microcontroller.
08/26/2024 Module 2

30. 30
Input devices
• Some microcontrollers provide an internal/external analogue-to-
digital converter (ADC) to convert analog quantities to digital
values.
• Resolution of the ADC will depend upon the number of bits used.
08/26/2024 Module 2

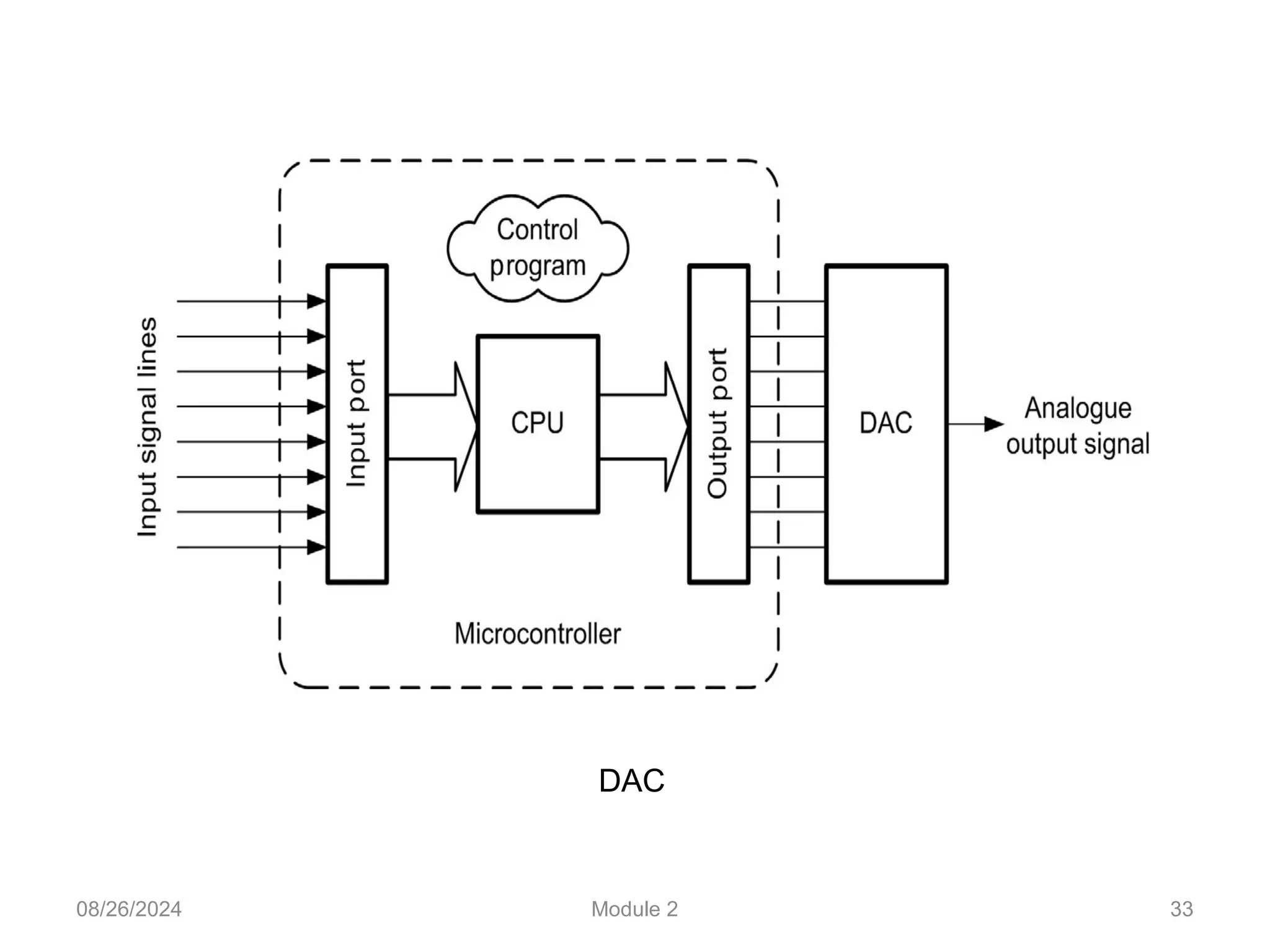
31. 08/26/2024 Module 2 31
ADC [1]

32. 32
Output devices
• Output devices used to communicate information or actions from the processor/
controller to the outside world.
• Example: LEDs, piezoelectric sounders, relays and motors.
• To be connected directly to the output port of a microcontroller, an output device
must accept a logic compatible signal.
• Where analog quantities required at the output a digital-to-analogue converter
(DAC) will be needed.
• Output resolution of a DAC depends on the number of bits.
08/26/2024 Module 2

33. 08/26/2024 Module 2 33
DAC

34. 34
Interface circuits
• Where input and output signals are not logic compatible, some
additional interface circuitry required in order to shift the voltage
levels or to provide additional current drive.
• Additional circuitry may also be required when a load (such as a relay
or motor) requires more current than is available from a standard logic
device or output port.
• For example, a common range of interface circuits (solid-state relays)
is available that will allow a microcontroller to be easily interfaced to
an a.c. mains-connected load.
08/26/2024 Module 2

35. 35
HALF-ADDER
A combinational circuit that performs the addition of two bits.
• Therefore, half-adder has two inputs and two outputs, SUM and CARRY.
• Boolean expressions for SUM and CARRY are
• SUM = AB’+A’B
• CARRY = AB
• These expressions shows that, SUM output is EX-OR gate and the CARRY output is
AND gate.
08/26/2024 Module 2

36. 36
FULL ADDER
Performs addition of three bits(two significant bits and a previous carry)
is a full adder.
S = x’y’z + x’yz’ + xy’z’ + xyz
C = xy + xz + yz
Module 2

37. 37
08/26/2024 Module 2

38. 38
Multiplexers
• Multiplexer is a special type of combinational circuit.
• n-data inputs, one output and m select inputs with 2m
= n.
• It is a digital circuit which selects one of the n data inputs and routes it to the
output based upon data on the select lines.
08/26/2024 Module 2
• Depending on the digital code
applied at the selected inputs, one
out of n data sources is selected
and transmitted to the single
output Y.
• E is called the strobe or enable
input (usually active low).

39. 39
8:1 Multiplexer
Fig reference: [2]
08/26/2024 Module 2

40. 40
Decoders :
• The decoder is called n-to-m-line decoder, where m≤2n
.
• 3-to-8 line decoder: For each possible input combination, there
are seven outputs that are equal to 0 and only one that is equal to
1.
08/26/2024 Module 2

41. 41
Shift Register
08/26/2024 Module 2
4-bit SISO register

42. 42
Type of shift register
1. SISO
2. SIPO
3. PIPO
4. PISO
08/26/2024 Module 2

43. 43
08/26/2024 Module 2

44. 44
Counters
• Sequential logic circuits that proceed through a well defined sequence
of states after application of clock pulses.
• Special type of registers with a capability of counting with the
application of clock pulse
• Used to count pulses
• Constructed using Flipflops and logic gates
• Counters are classified into two categories :
Ripple (or Asynchronous ) Counters
Synchronous Counters
08/26/2024 Module 2

45. 45
Asynchronous Counters
Fig: Asynchronous counter
08/26/2024 Module 2

46. 08/26/2024 Module 2 46
Asynchronous Counters
• Data ripples from the output of one flip flop to the input of the next (ripple counter).
• Output of one flip flop acts as clock to next flip flop.
• In 3 bit asynchronous counter, output of first flip flop toggles for every negative edge
of clock signal.
• Output of second flip flop toggles for every negative edge of output of first flip flop.
• Output of second flip flop toggles for every negative edge of output of first flip flop.
Synchronous Counters
• All flip flops are clocked simultaneously.
• Example: ring counter and johnson counter.

47. 08/26/2024 Module 2 47
• Design a 3-to-8 Decoder and show its implementation using basic gates.
• Construct a logic circuit that will produce a Logic 1 output whenever two or
more of its inputs are at Logic 1.
• With the help of truth table explain full adder using logic gates.
• Explain Input and output states for a J-K bistable using clocked operation.
• With the help of a neat diagram explain the 4-bit shift register operation and
types.
• With a neat block diagram explain the arrangement of a microcontroller
system with typical inputs and outputs.
• Discuss the design of a 3-bit asynchronous up-counter.
• With a neat block diagram show how typical input and output blocks are
connected to a microcontroller unit.
• With the help of a timing diagram explain how D-type bistable circuit works.
• Design a full adder using two half adders and an OR-gate.
• Design a 4-stage shift register using J-K bistables.
• Write a note on different data types mentioning the bit size and range of values
supported.
Model Question Paper Questions

48. 08/26/2024 Module 2 48
Reference:
1. Mike Tooley, ‘Electronic Circuits, Fundamentals &
Applications’, 4th Edition, Elsevier, 2015. DOI
https://doi.org/10.4324/9781315737980. eBook
ISBN9781315737980
2. D P Kothari, I J Nagrath, ‘Basic Electronics’, 2nd edition,
McGraw Hill Education (India), Private Limited, 2018.