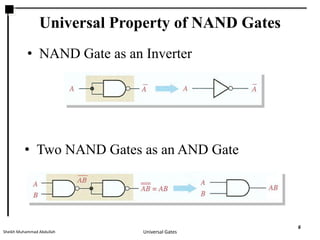
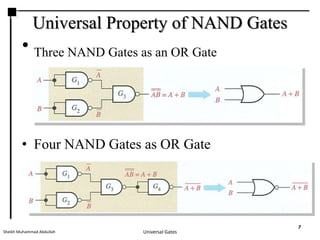
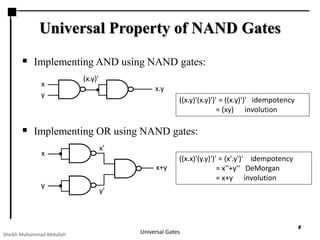
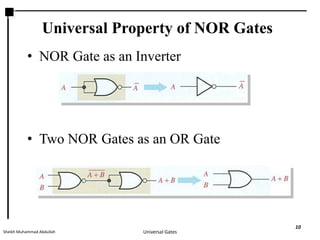
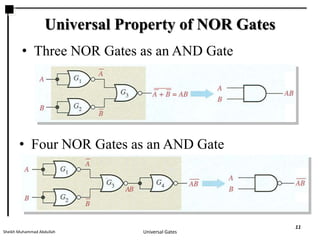
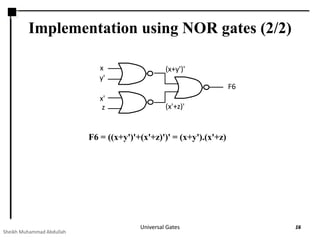
This presentation discusses NAND and NOR gates and their universal properties. It explains that NAND and NOR gates can be used to implement any other logic function, making them universal gates. The document provides examples of how to implement AND, OR, and INVERTER gates using only NAND gates or only NOR gates. It also gives procedures for implementing any Boolean logic expression using a network of only NAND gates or only NOR gates.

1. WELCOME
To Our Presentation
1Sheikh Muhammad Abdullah Universal Gates

2. Our Topics name:
2
NAND and NOR gates are “Universal” because they can
used to produce any of the other logic functions.
Sheikh Muhammad Abdullah Universal Gates

3. MUHAMMAD ABDULLAH(142-0076-511)
MD.KHALID HASAN(142-0106-501)
MD.IBRAHIM(141-0036-511)
Department Name: B.Sc in EEE&CSE
3
Teacher’s Name:
MUHAMMAD WOLI ULLAH
Our Team name:
Subject Name: DIGITAL LOGIC
Sheikh Muhammad Abdullah Universal Gates

4. Sheikh Muhammad Abdullah
Universal Gates 4
Universal Gates: NAND and NOR
 AND/OR/NOT gates are sufficient for building any
Boolean functions.
 We call the set {AND, OR, NOT} a complete set of logic.
 However, other gates are also used because:
(i) usefulness
(ii) economical on transistors
(iii) self-sufficient
NAND/NOR: economical, self-sufficient
XOR: useful (e.g. parity bit generation)

5. Sheikh Muhammad Abdullah
Universal Gates 5
Universal Property of NAND Gates
 NAND gate is self-sufficient (can build any logic circuit
with it).
 Therefore, {NAND} is also a complete set of logic.
 Can be used to implement AND/OR/NOT.
1. Implementing an inverter using NAND gate:
(x.x)' = x' (T1: idempotency)
x x'

6. Universal Property of NAND Gates
• NAND Gate as an Inverter
• Two NAND Gates as an AND Gate
Sheikh Muhammad Abdullah Universal Gates
6

7. Universal Property of NAND Gates
• Three NAND Gates as an OR Gate
• Four NAND Gates as OR Gate
Sheikh Muhammad Abdullah Universal Gates
7

8. Universal Property of NAND Gates
((x.y)'(x.y)')' = ((x.y)')' idempotency
= (xy) involution
((x.x)'(y.y)')' = (x'.y')' idempotency
= x''+y'' DeMorgan
= x+y involution
 Implementing AND using NAND gates:
 Implementing OR using NAND gates:
x
x.y
y
(x.y)'
x
x+y
y
x'
y'
Sheikh Muhammad Abdullah Universal Gates
8

9. Universal Property of NOR Gates
 NOR gate is also self-sufficient.
 Therefore, {NOR} is also a complete set of logic
 Can be used to implement AND/OR/NOT.
 Implementing an inverter using NOR gate:
(x+x)' = x' (T1: idempotency)
x x'
Sheikh Muhammad Abdullah
Universal Gates 9

10. Universal Property of NOR Gates
• NOR Gate as an Inverter
• Two NOR Gates as an OR Gate
Sheikh Muhammad Abdullah Universal Gates
10

11. Universal Property of NOR Gates
• Three NOR Gates as an AND Gate
• Four NOR Gates as an AND Gate
Sheikh Muhammad Abdullah Universal Gates
11

12. Universal Property of NOR Gates
((x+x)'+(y+y)')'=(x'+y')' idempotency
= x''.y'' DeMorgan
= x.y involution
((x+y)'+(x+y)')' = ((x+y)')' idempotency
= (x+y) involution
 Implementing AND using NOR gates:
 Implementing OR using NOR gates:
x
x+y
y
(x+y)'
x
x.y
y
x'
y'
Sheikh Muhammad Abdullah
Universal Gates 12

13. Implementation using NAND gates (1/2)
 Possible to implement any Boolean expression using
NAND gates.
Procedure:
(i) Obtain sum-of-products Boolean expression:
e.g. F3 = x.y'+x'.z
(ii) Use DeMorgan theorem to obtain expression
using 2-level NAND gates
e.g. F3 = x.y'+x'.z
= (x.y'+x'.z)' ' involution
= ((x.y')' . (x'.z)')' DeMorgan
Sheikh Muhammad Abdullah
Universal Gates 13

14. Implementation using NAND gates (2/2)
F3 = ((x.y')'.(x'.z)') ' = x.y' + x'.z
x'
z
F3
(x'.z)'
(x.y')'x
y'
Sheikh Muhammad Abdullah
Universal Gates 14

15. Implementation using NOR gates (1/2)
 Possible to implement any Boolean expression using NOR
gates.
Procedure:
(i) Obtain product-of-sums Boolean expression:
e.g. F6 = (x+y').(x'+z)
(ii) Use DeMorgan theorem to obtain expression
using 2-level NOR gates.
e.g. F6 = (x+y').(x'+z)
= ((x+y').(x'+z))' ' involution
= ((x+y')'+(x'+z)')' DeMorgan
Sheikh Muhammad Abdullah
Universal Gates 15

16. Implementation using NOR gates (2/2)
F6 = ((x+y')'+(x'+z)')' = (x+y').(x'+z)
x'
z
F6
(x'+z)'
(x+y')'x
y'
Sheikh Muhammad Abdullah
Universal Gates 16

17. Sheikh Muhammad Abdullah
17
Mano, M. Morris (October 1992). Computer System Architecture (3rd ed. ed.).
Prentice-Hall. ISBN 0-13-175563-3
Universal Gates
John A. Camara (2010). Electrical and Electronics Reference Manual for the Electrical
and Computer PE Exam. www.ppi2pass.com. p. 41. ISBN 978-1-59126-166-7.

18. THANKS TO ALL
Sheikh Muhammad Abdullah 18Universal Gates