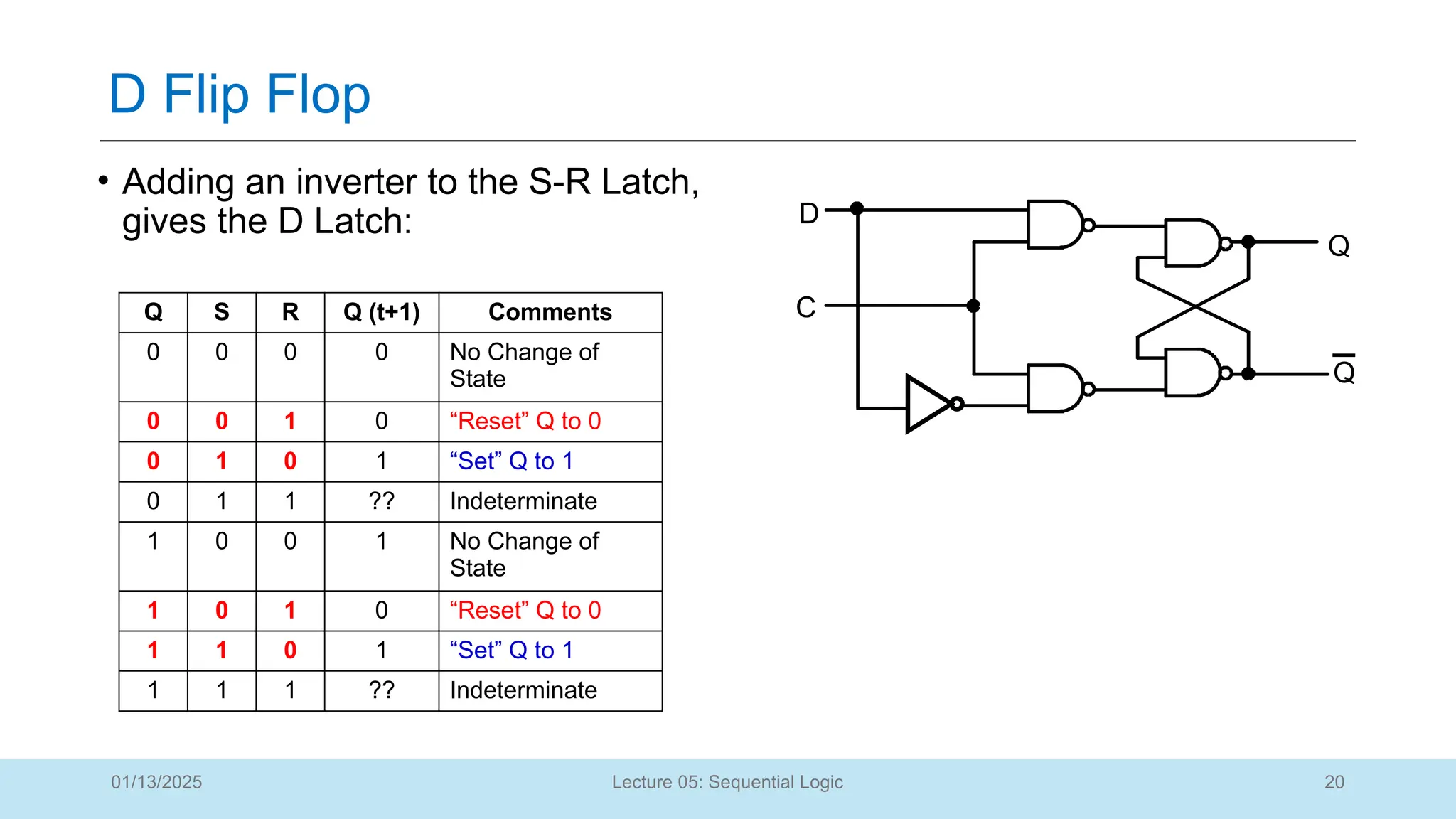
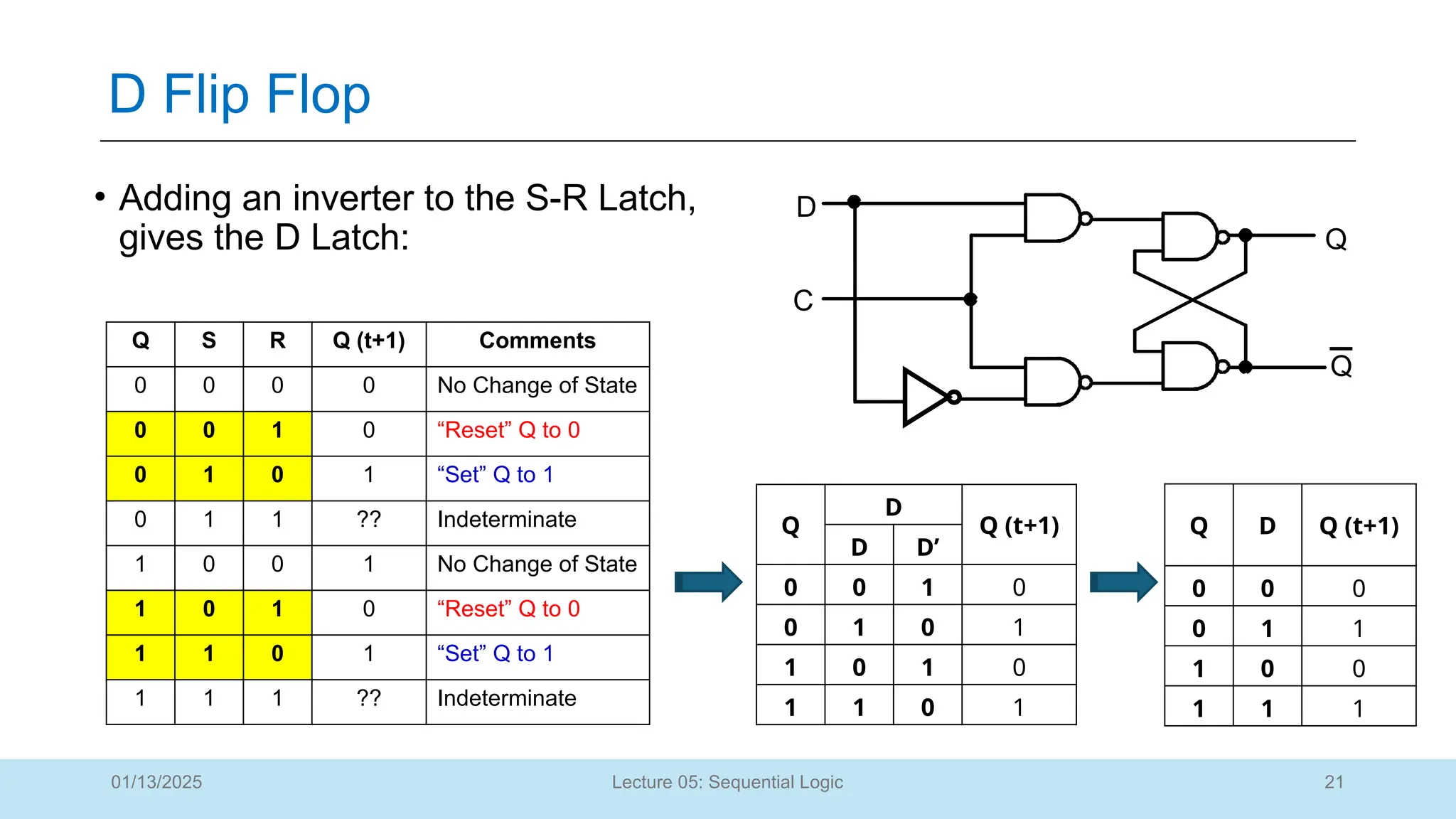
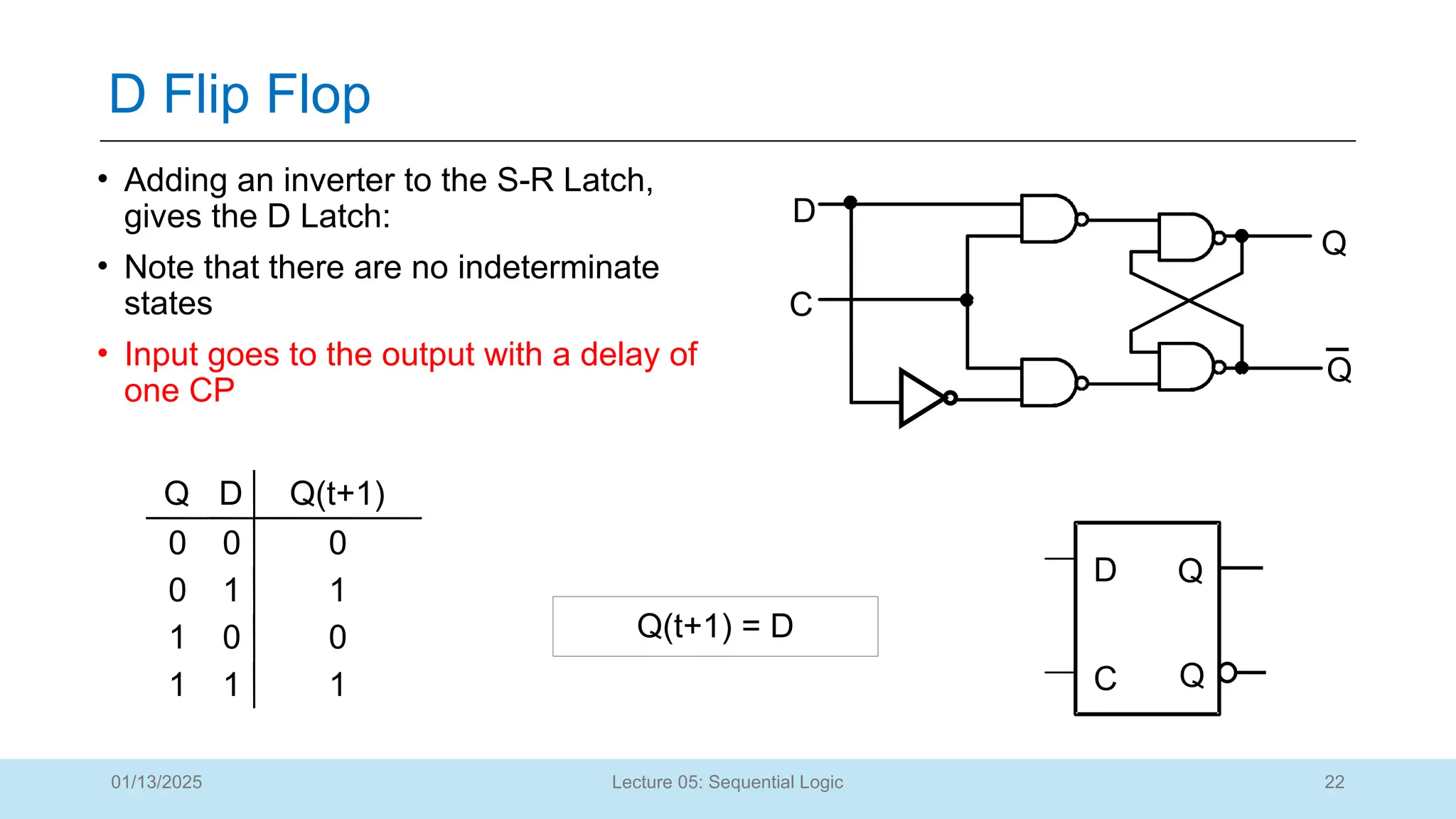
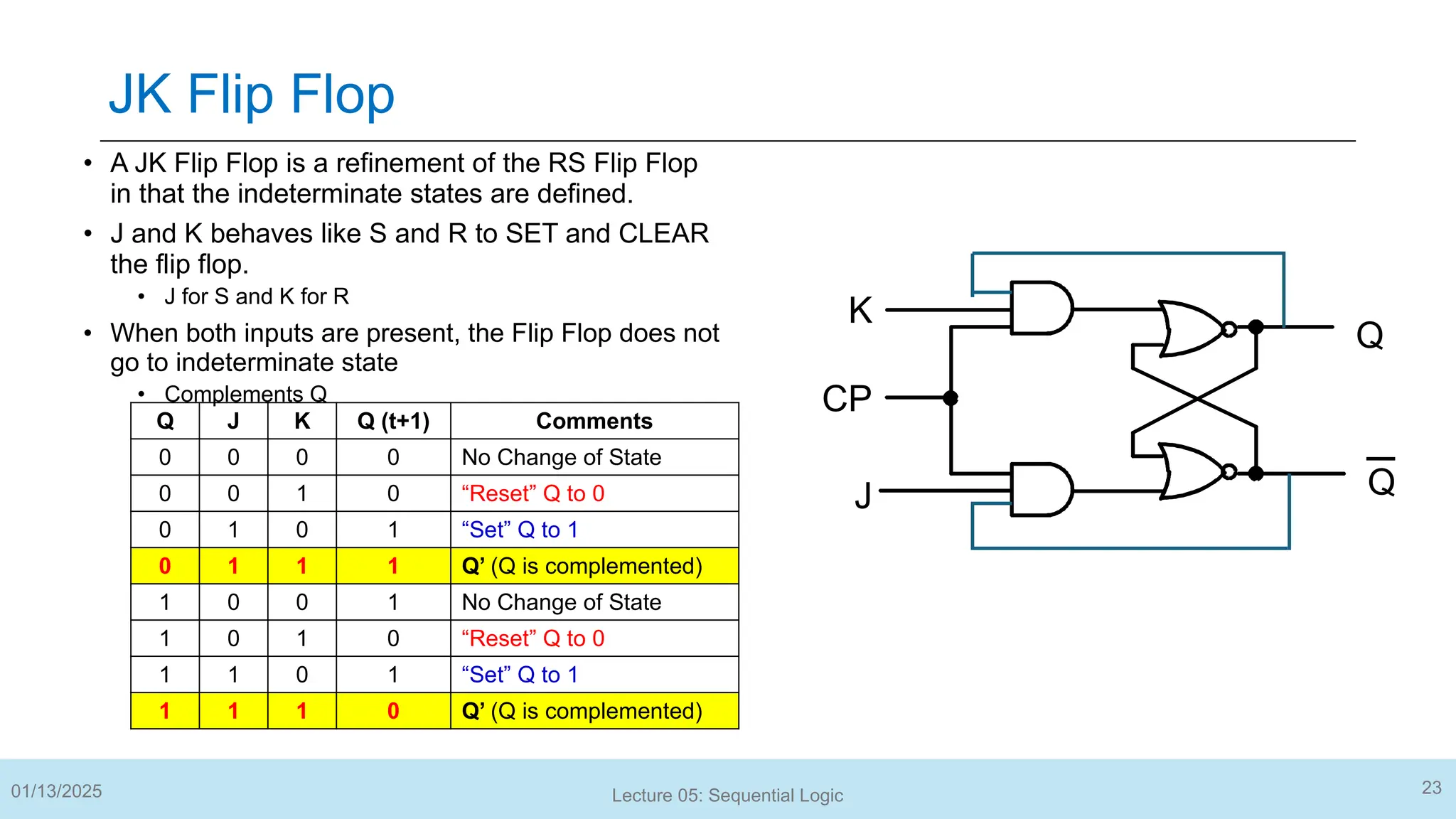
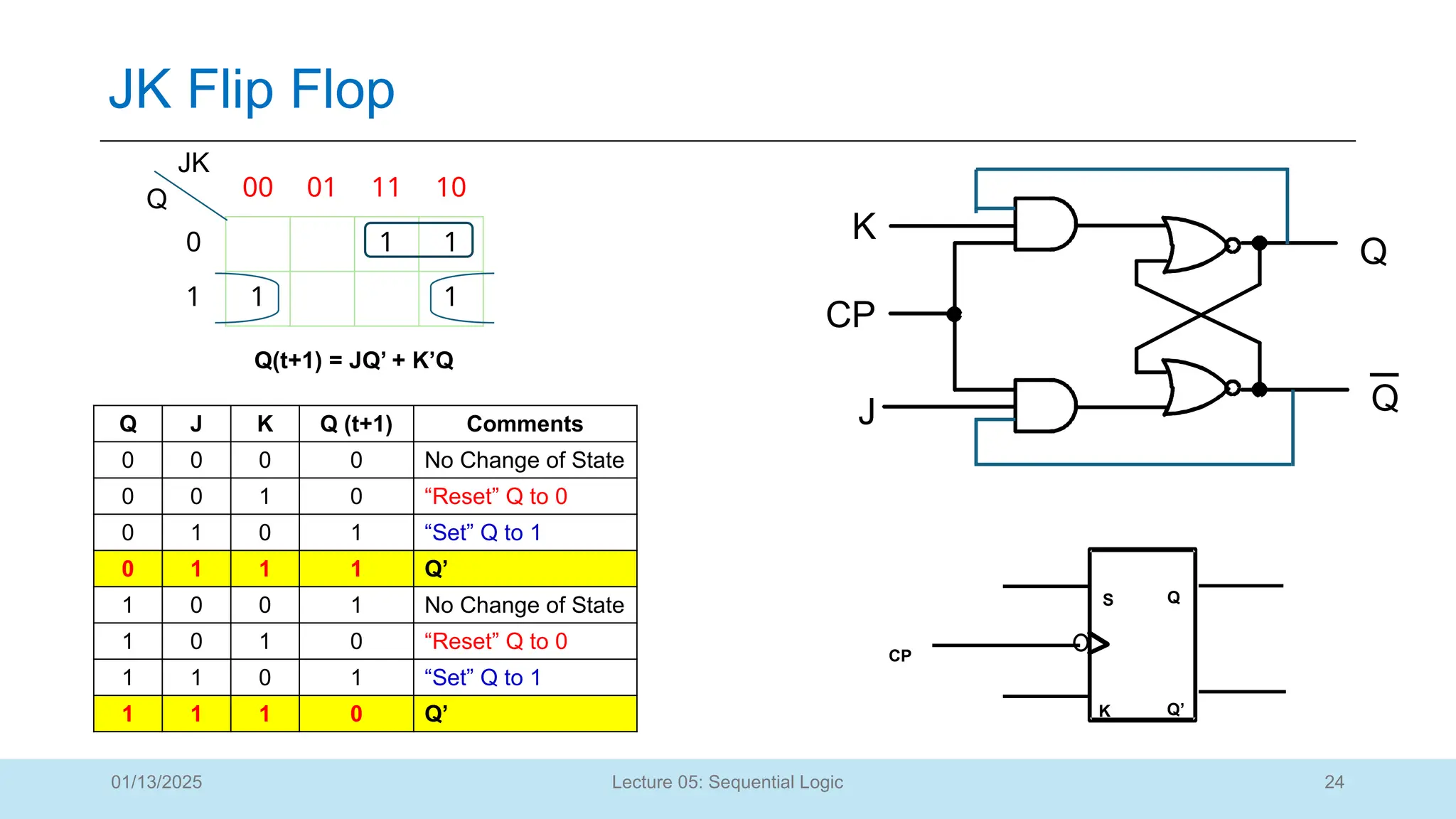
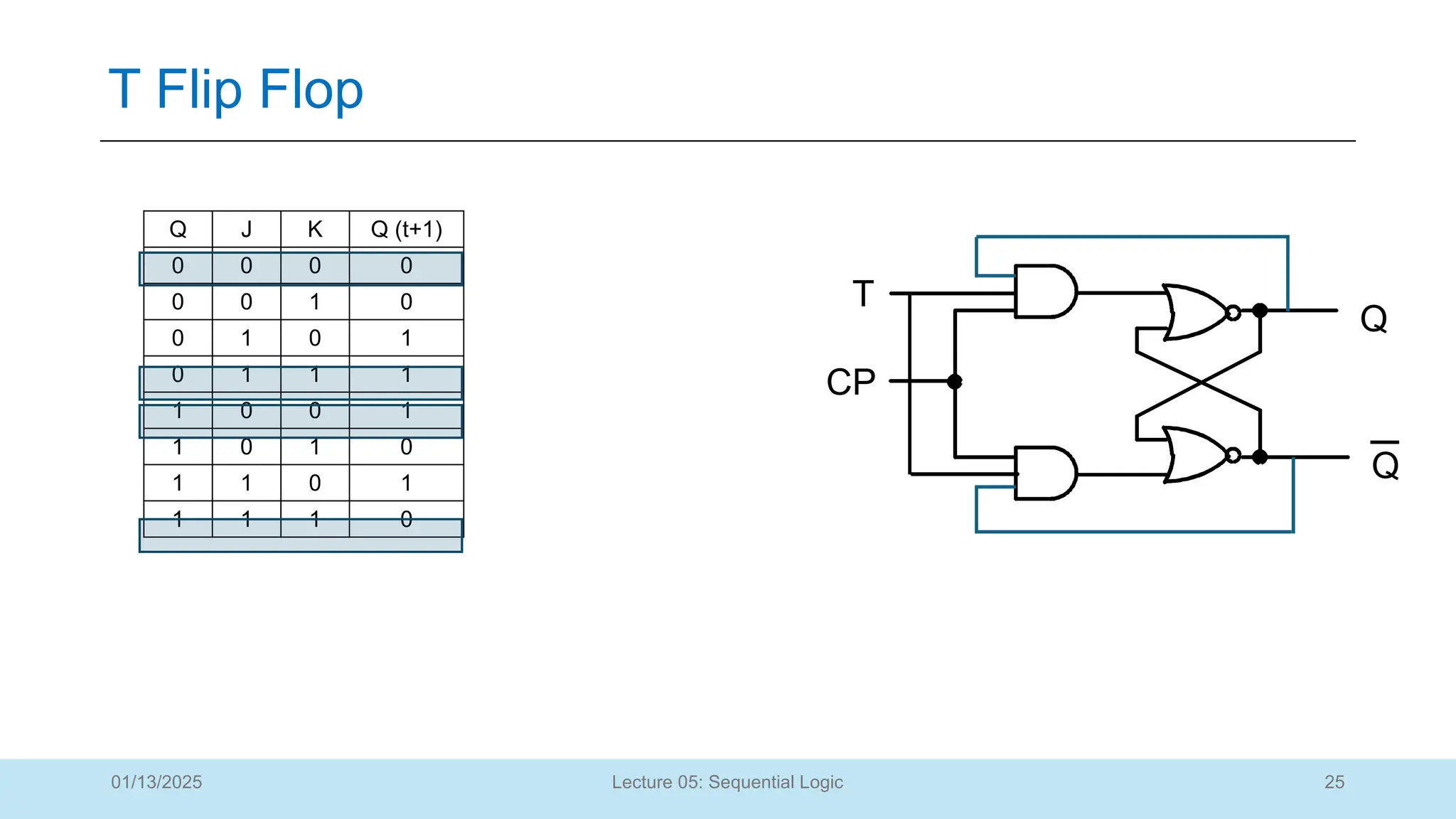
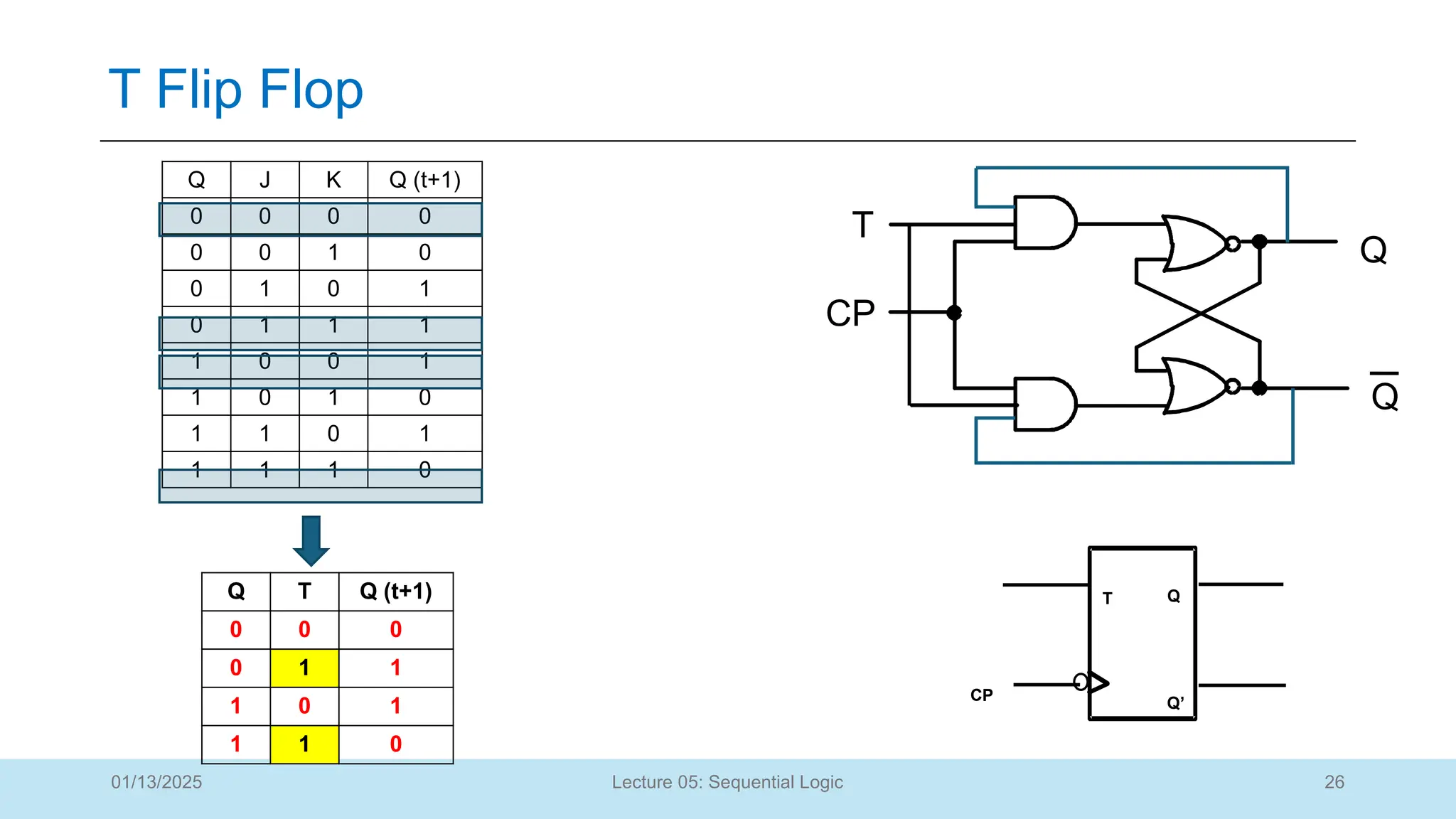
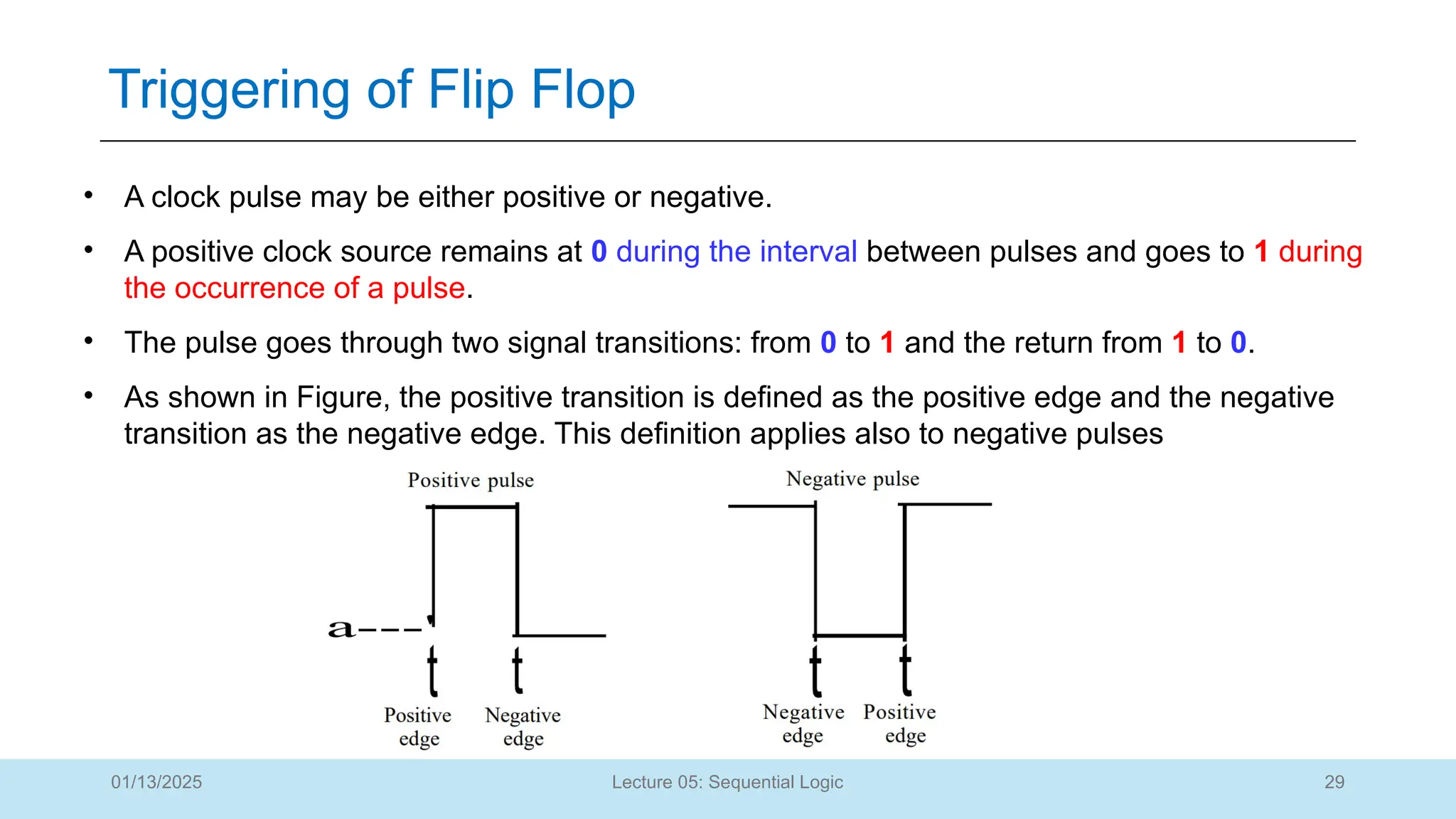
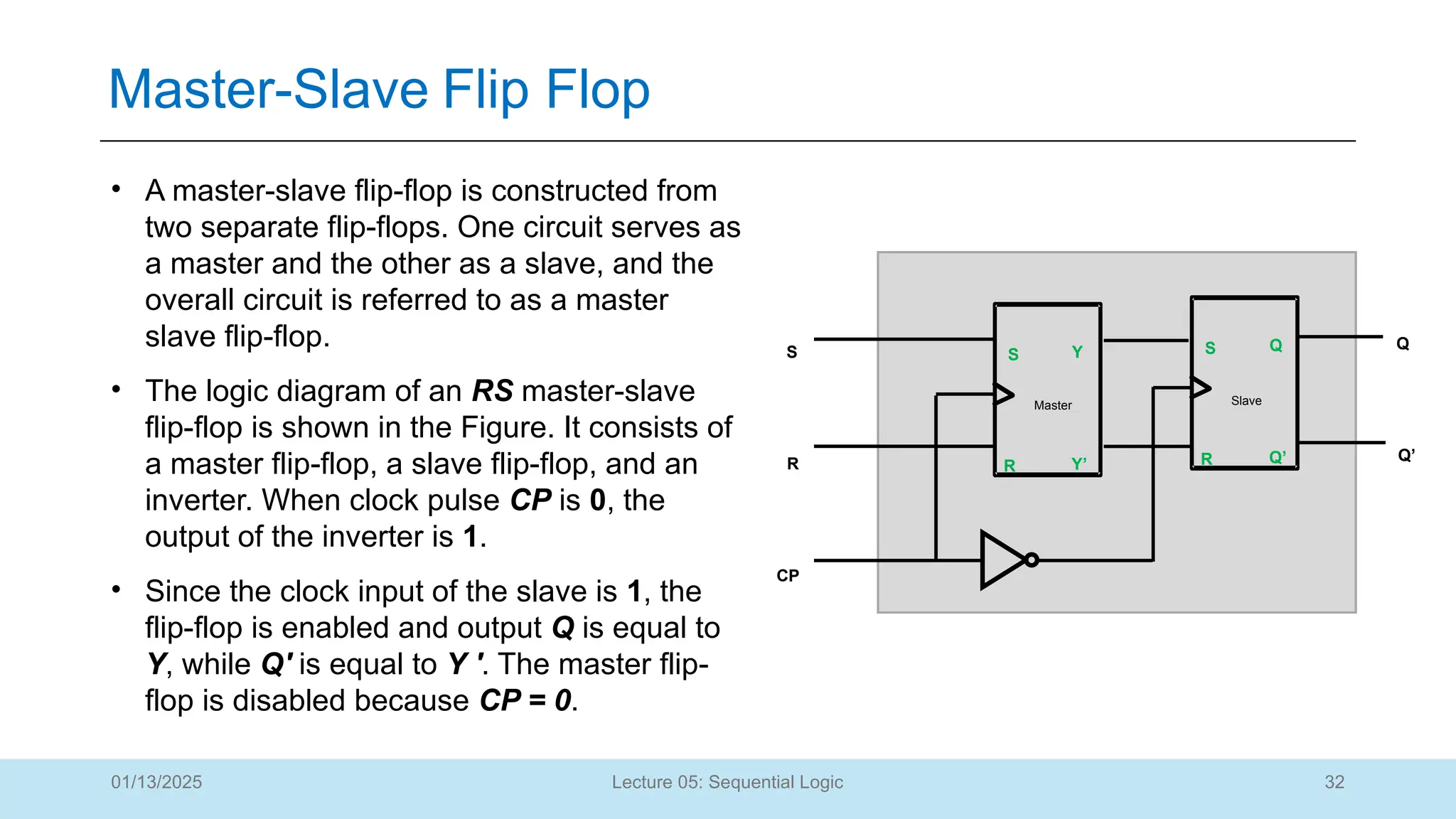
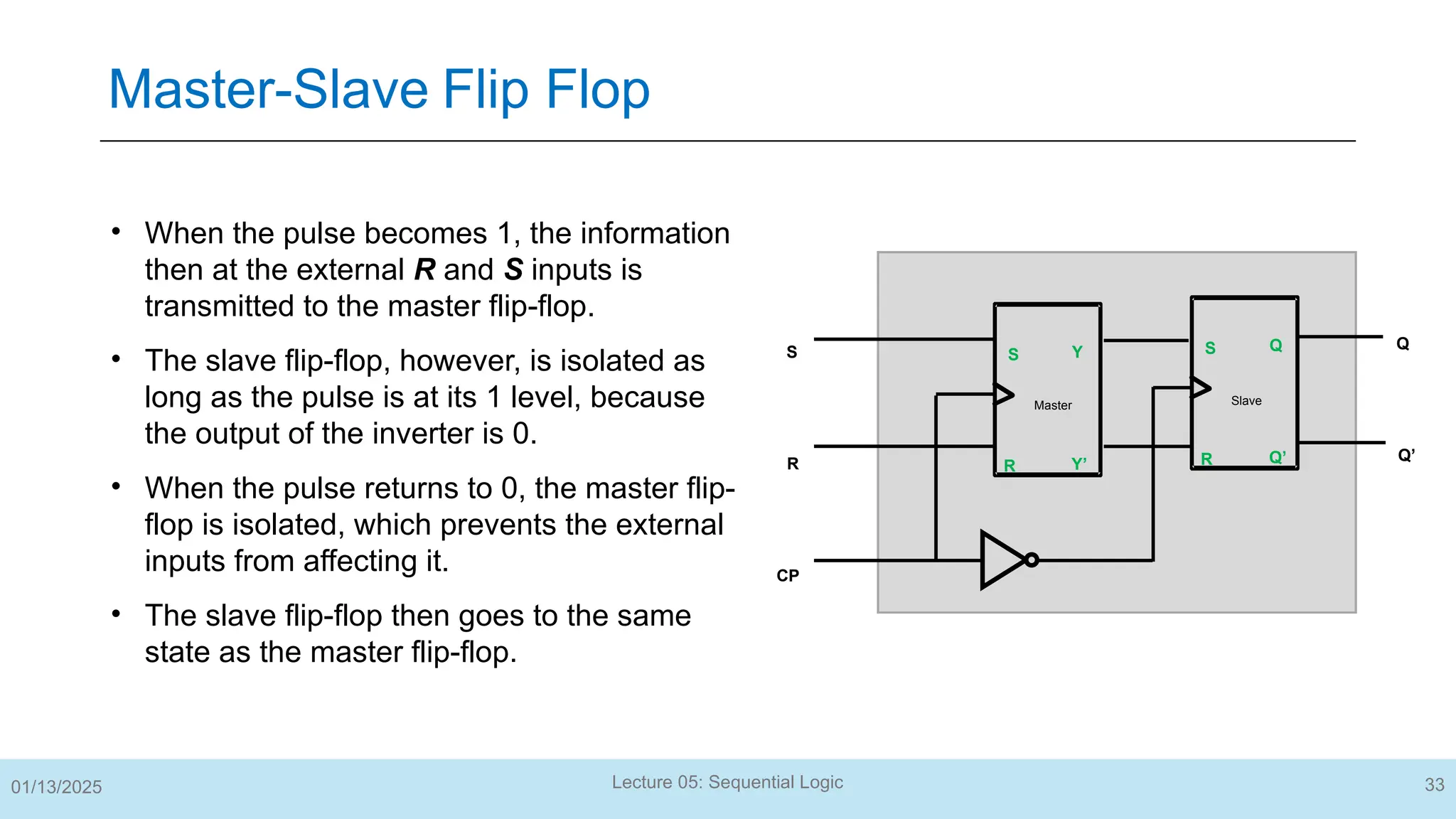
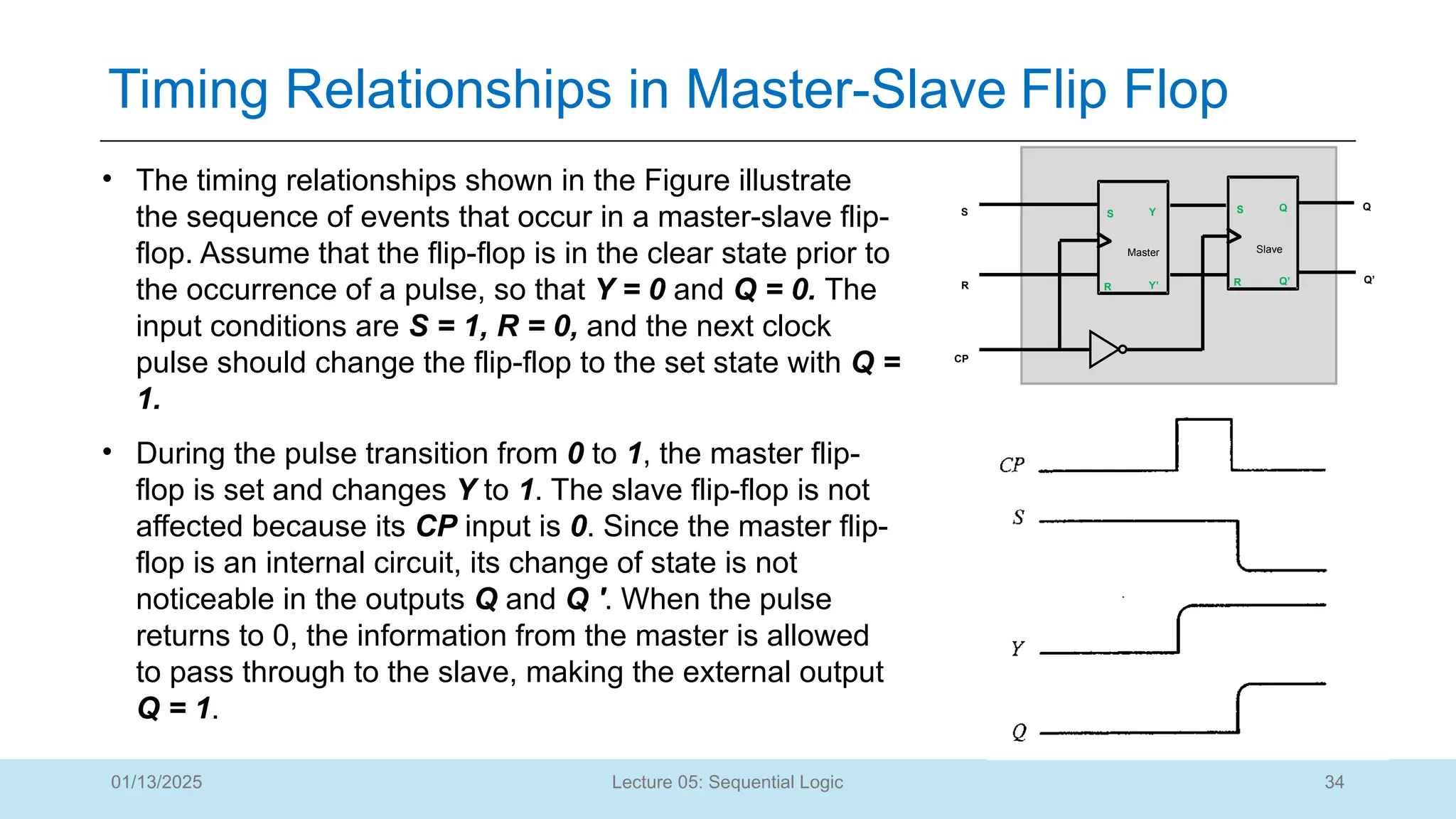
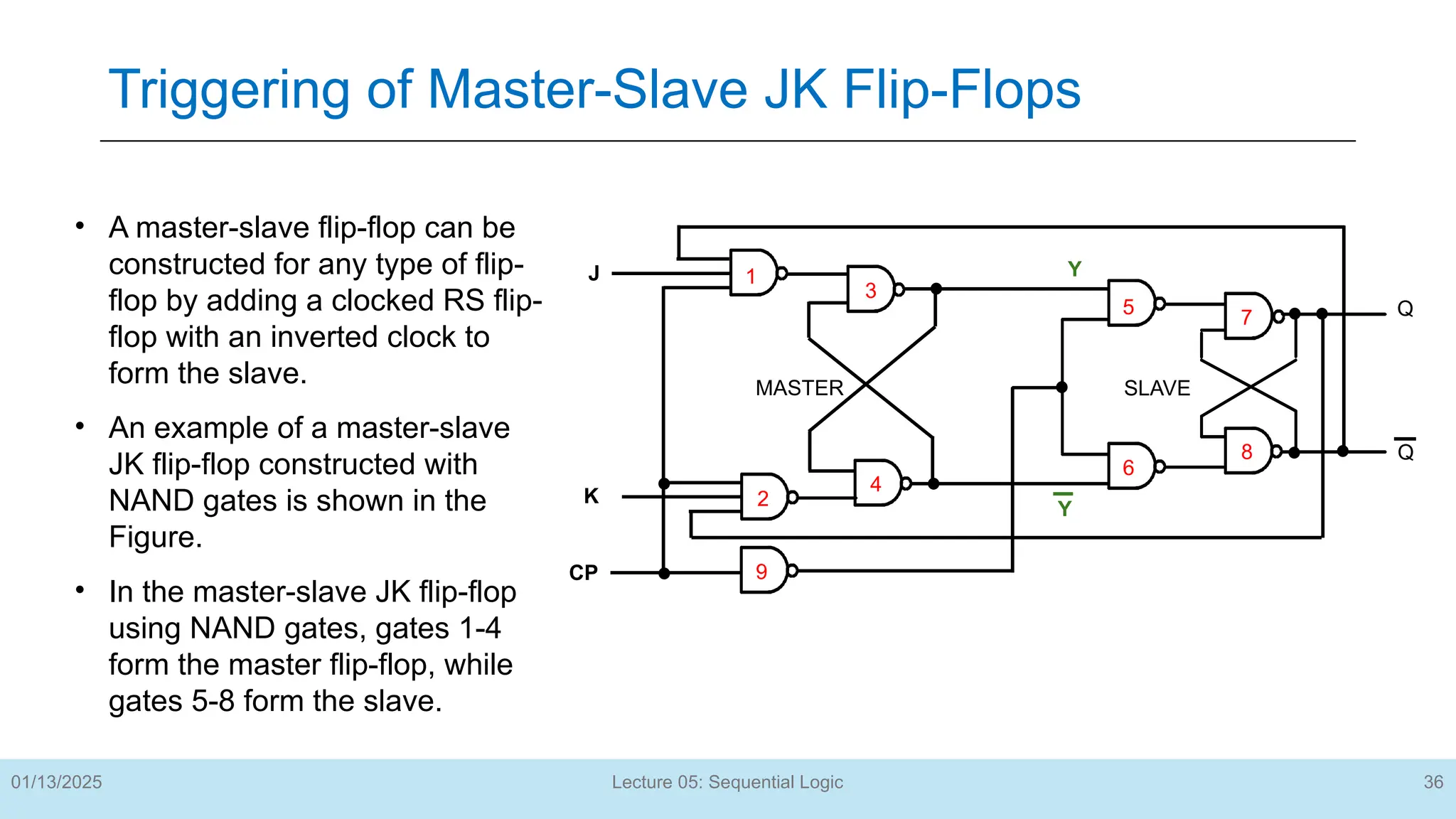
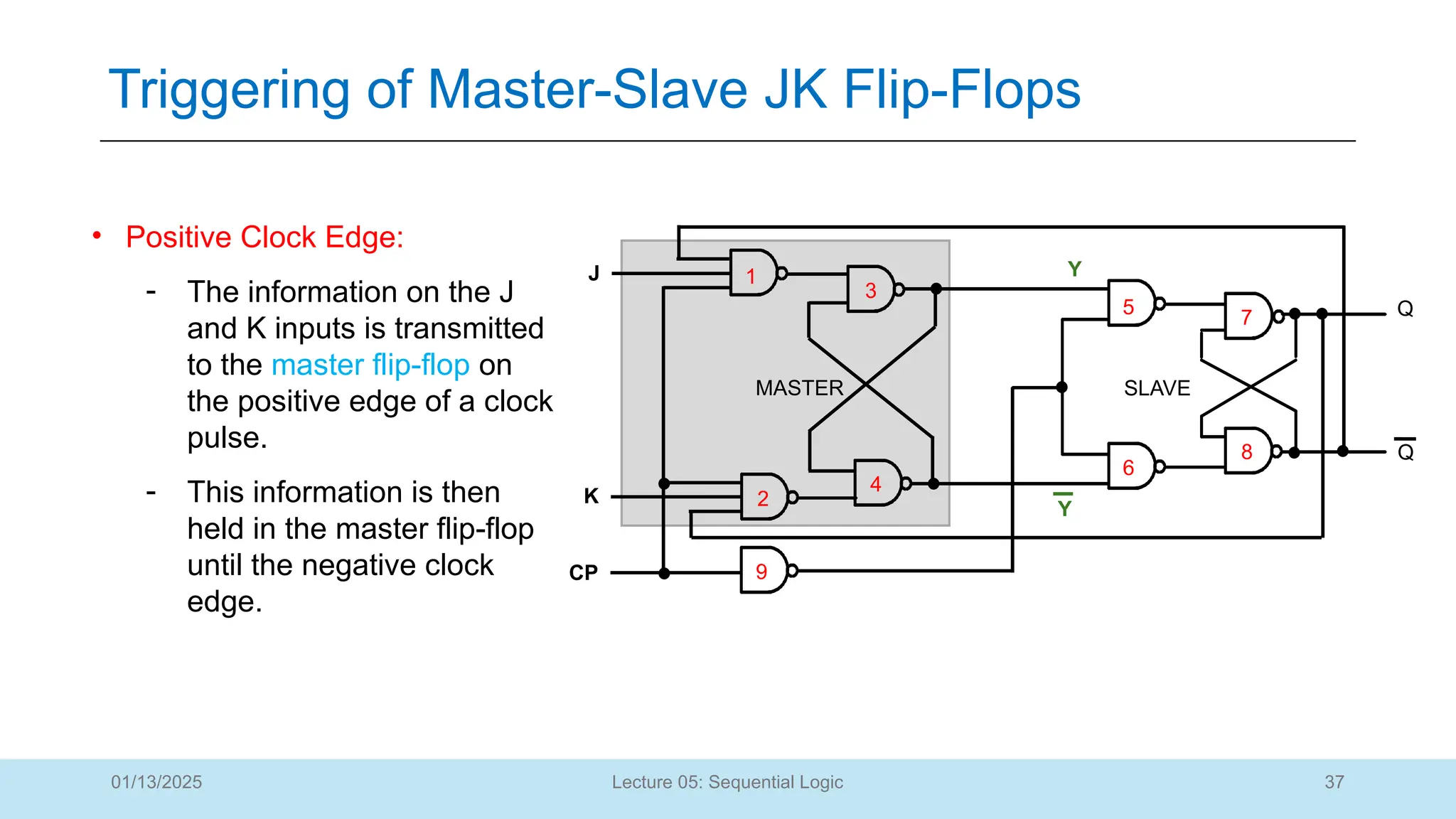
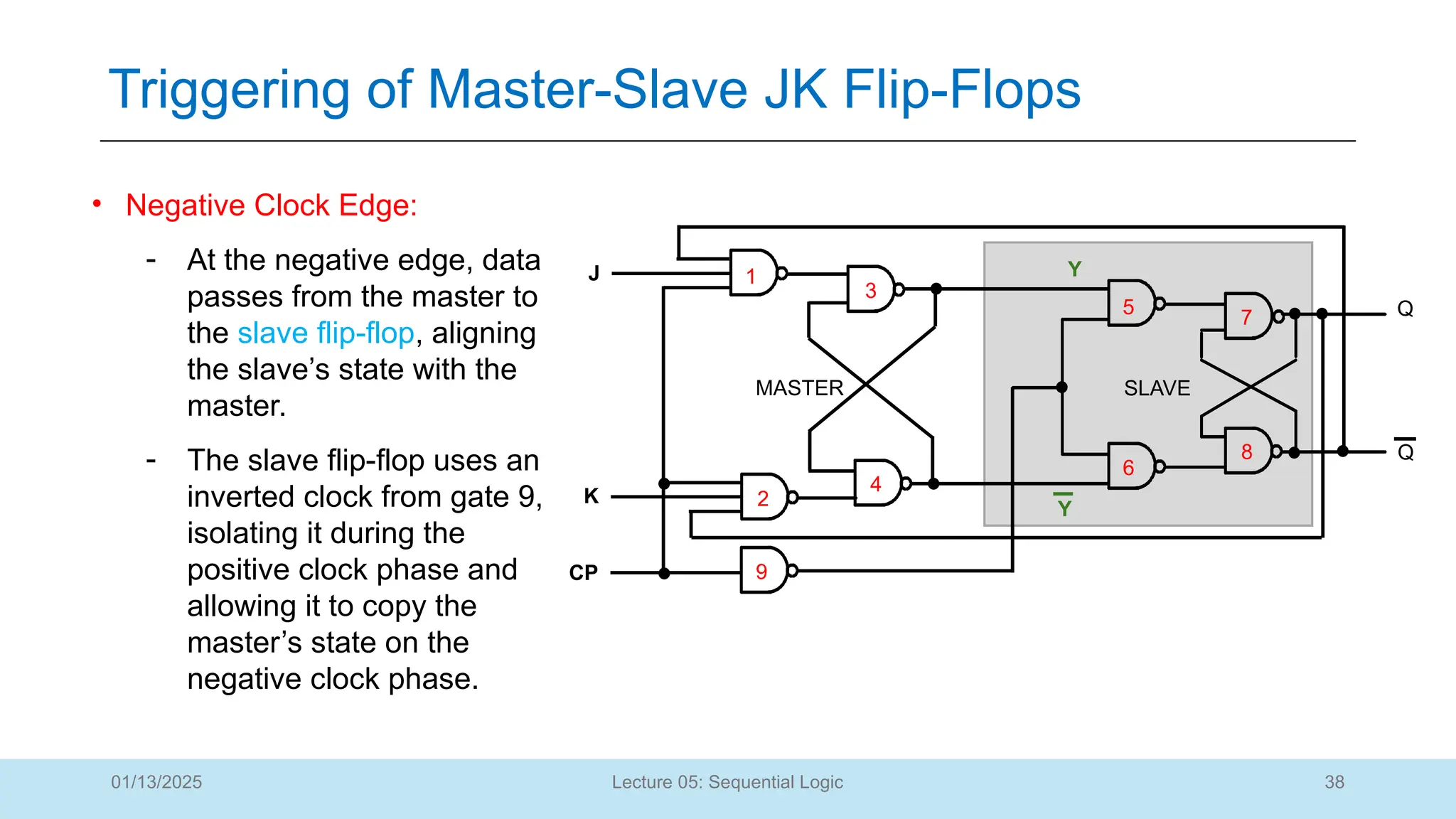
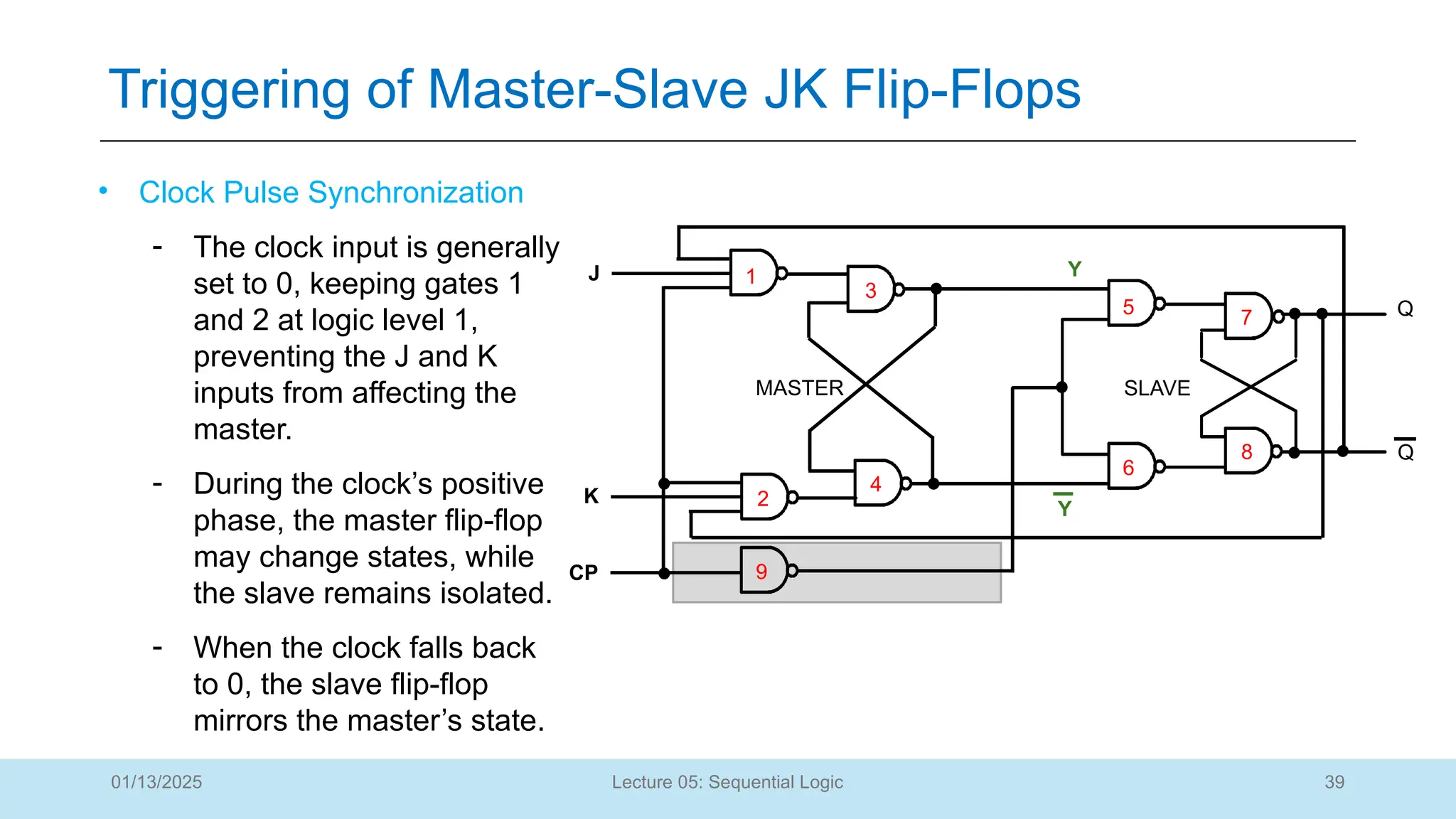
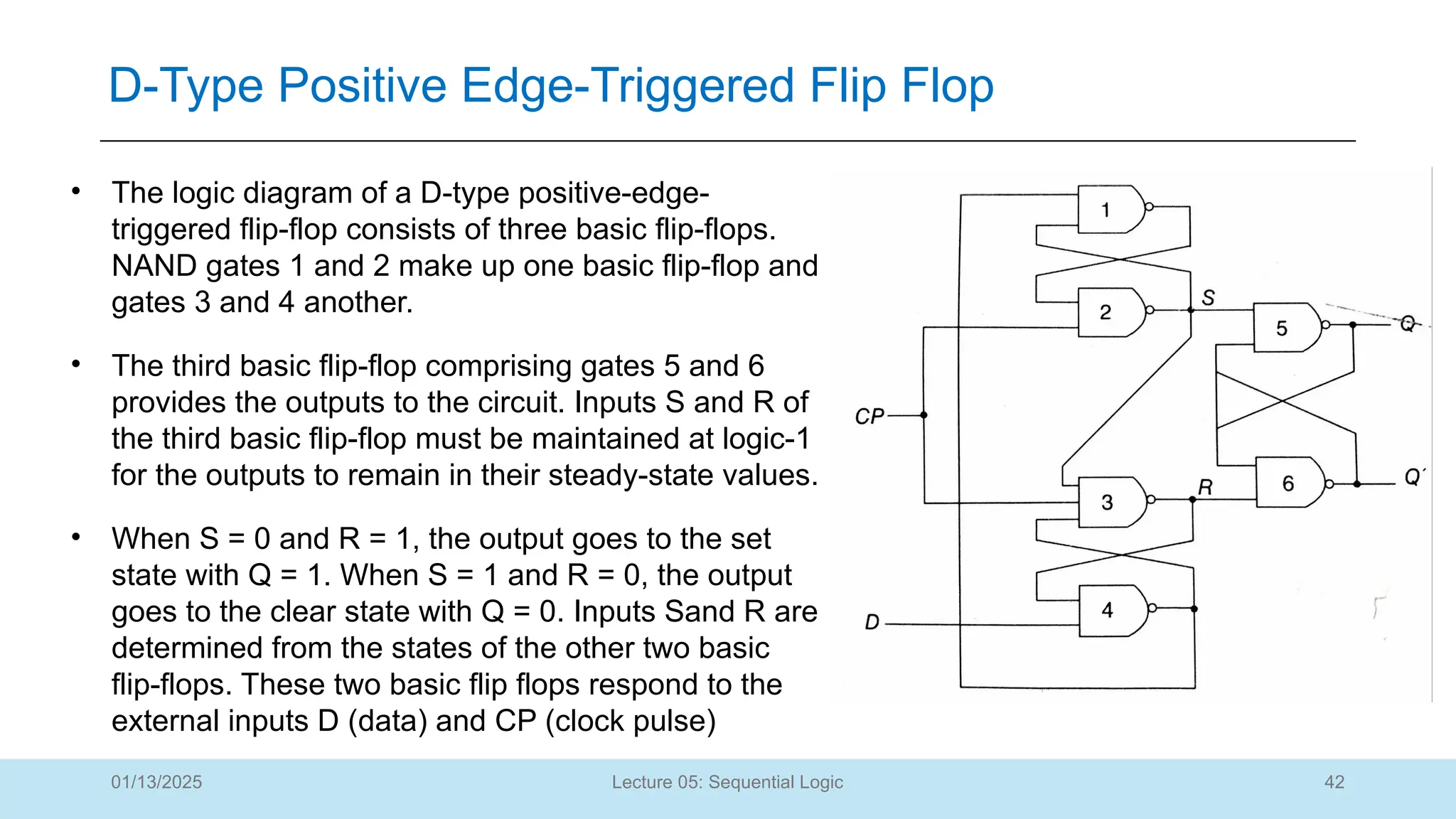
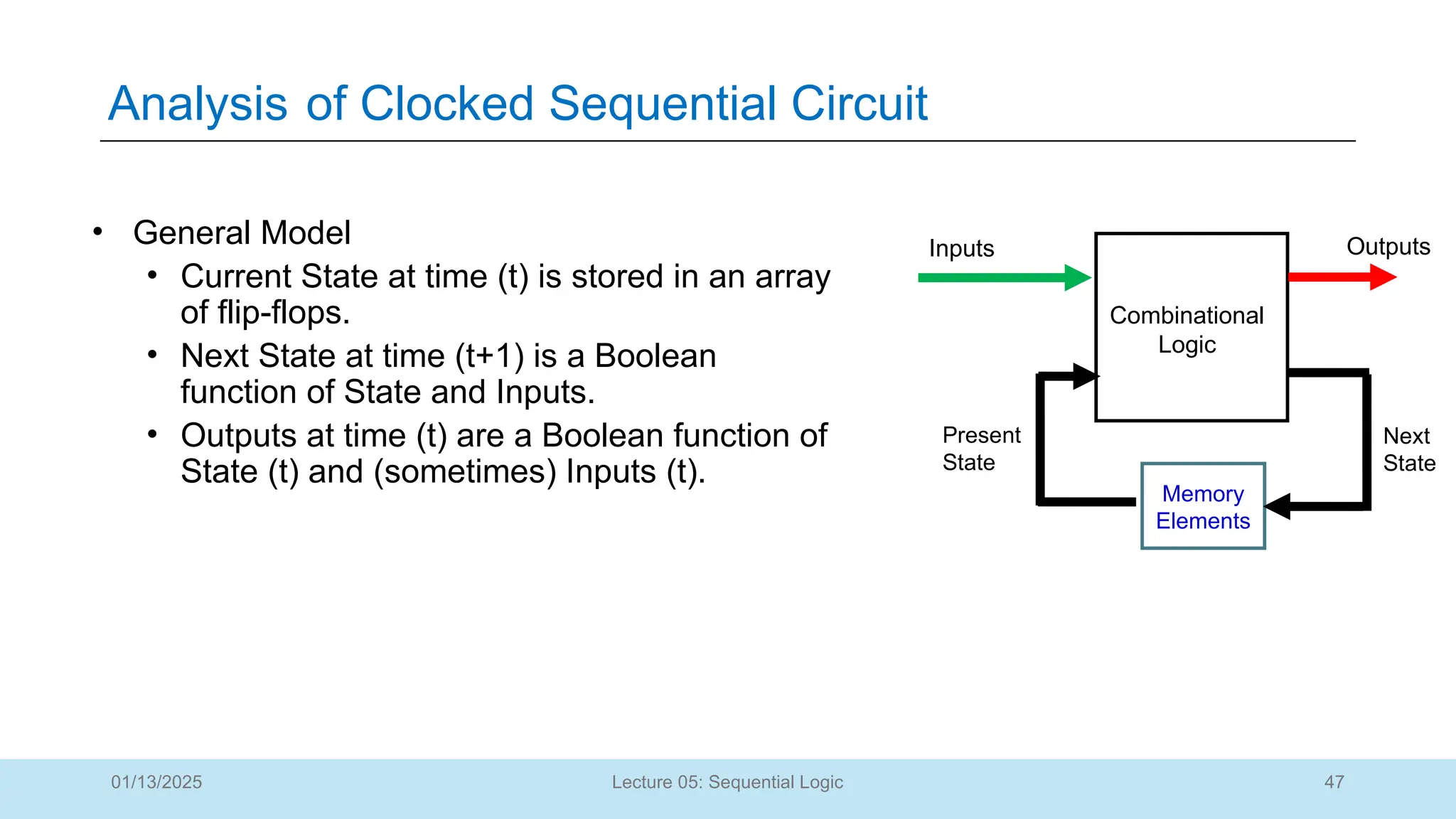
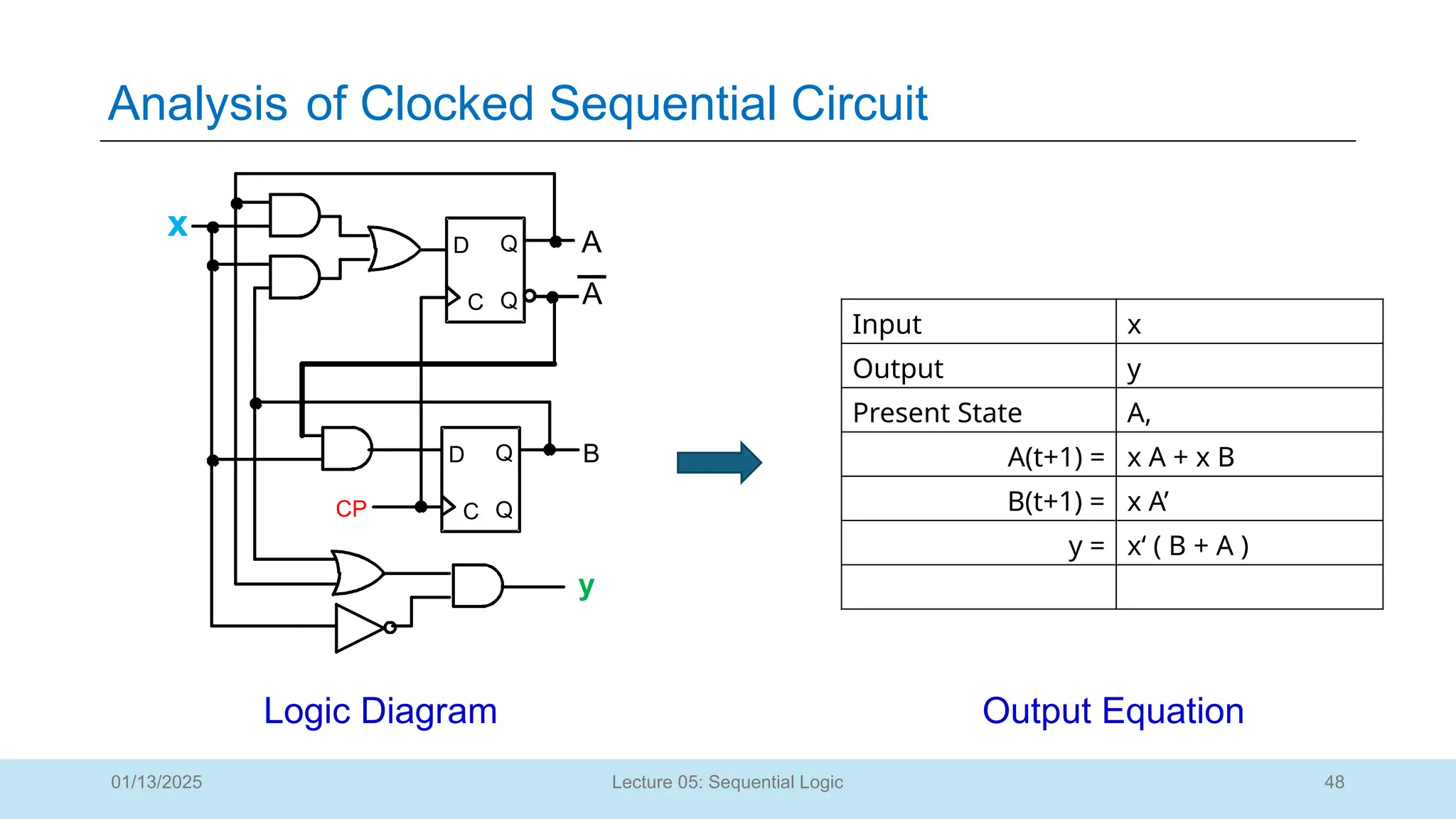
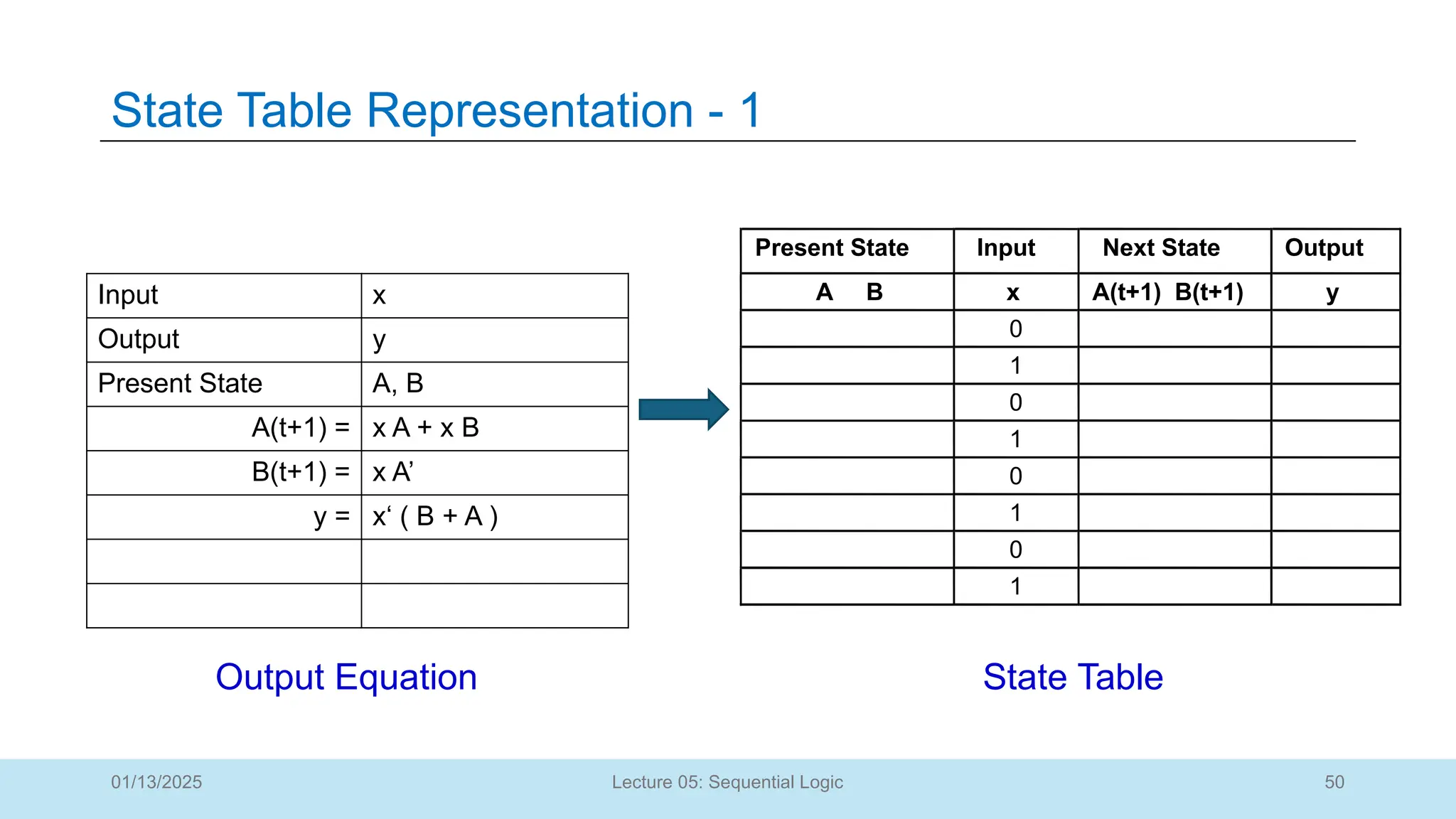
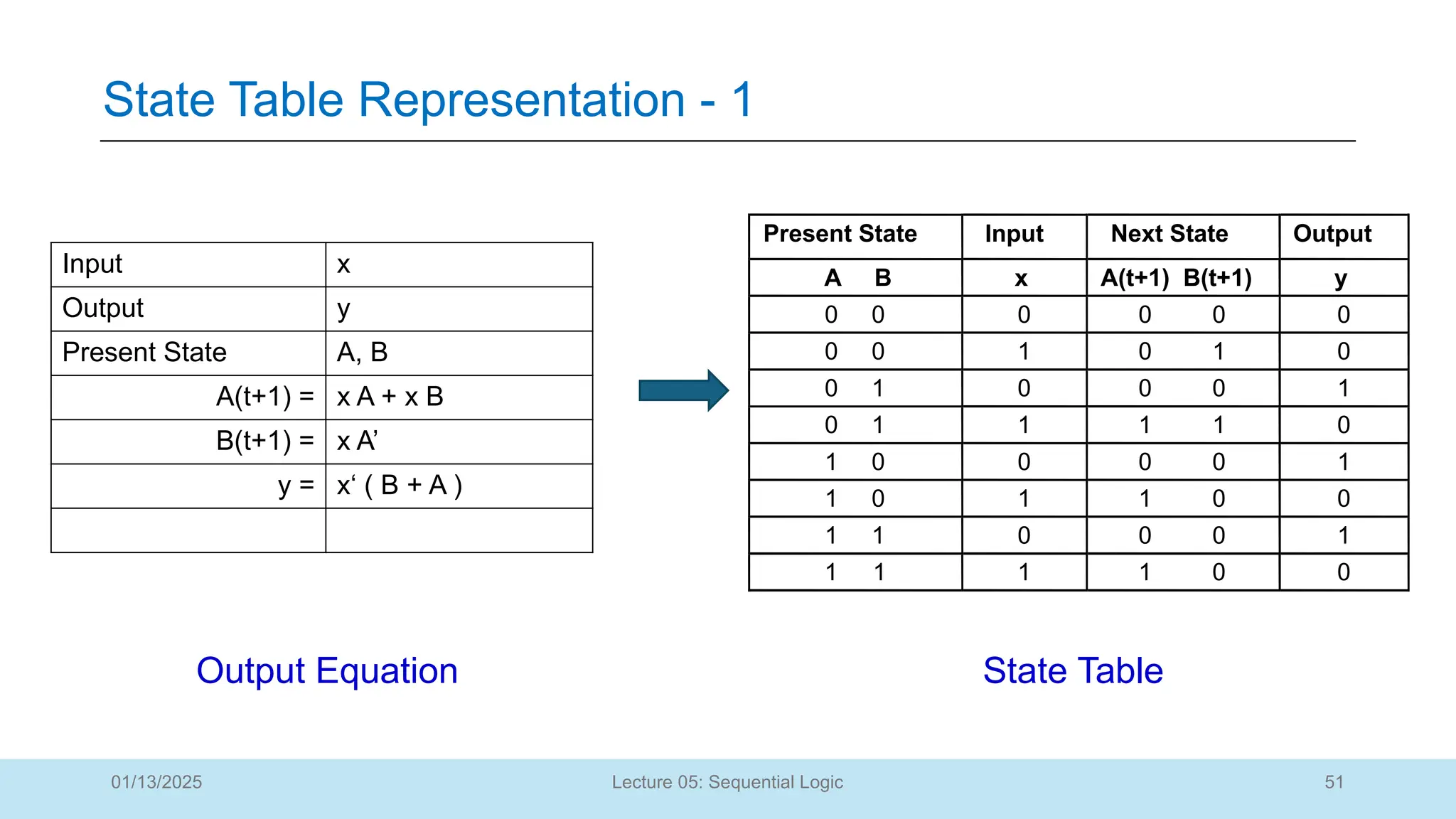
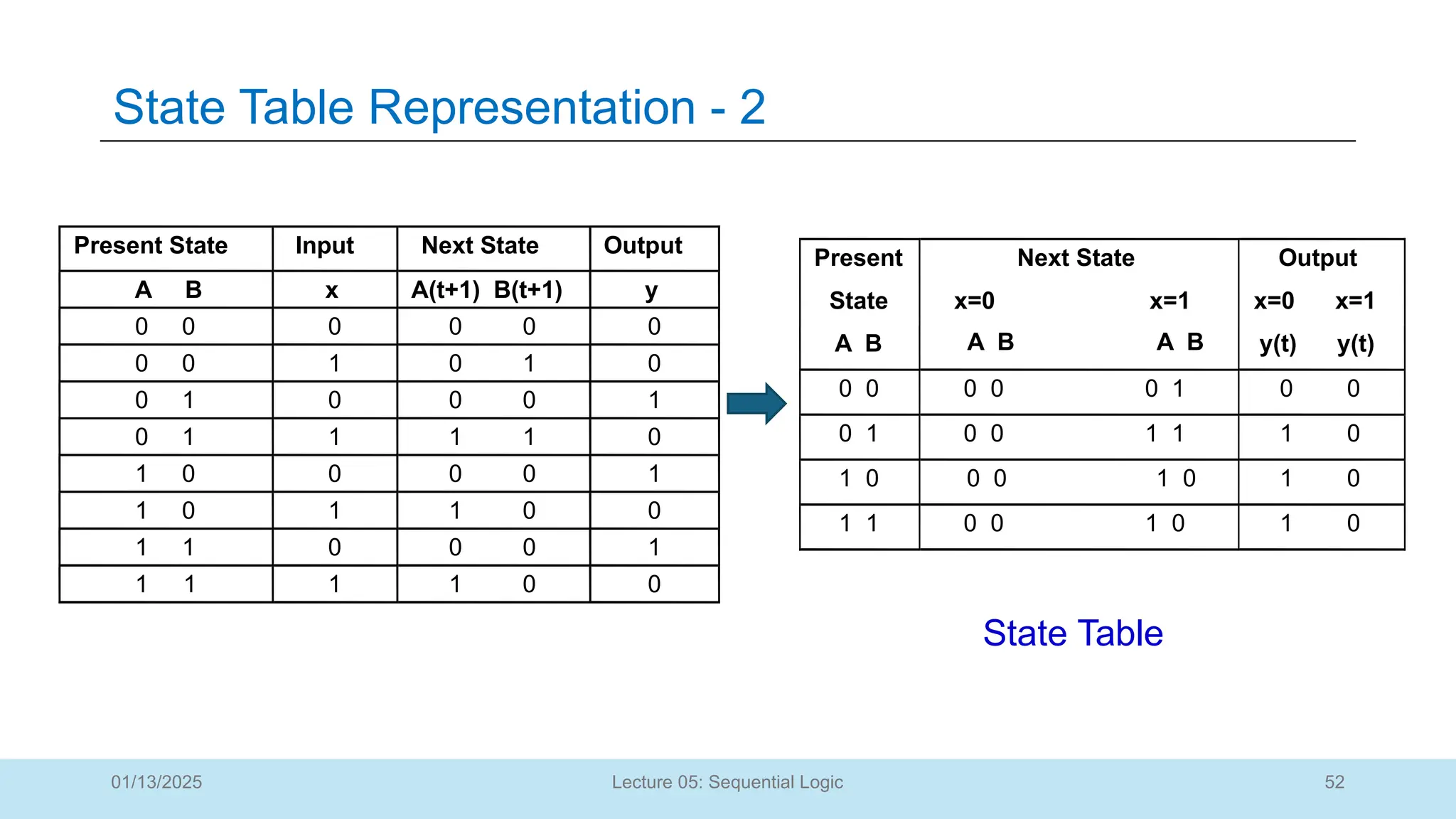
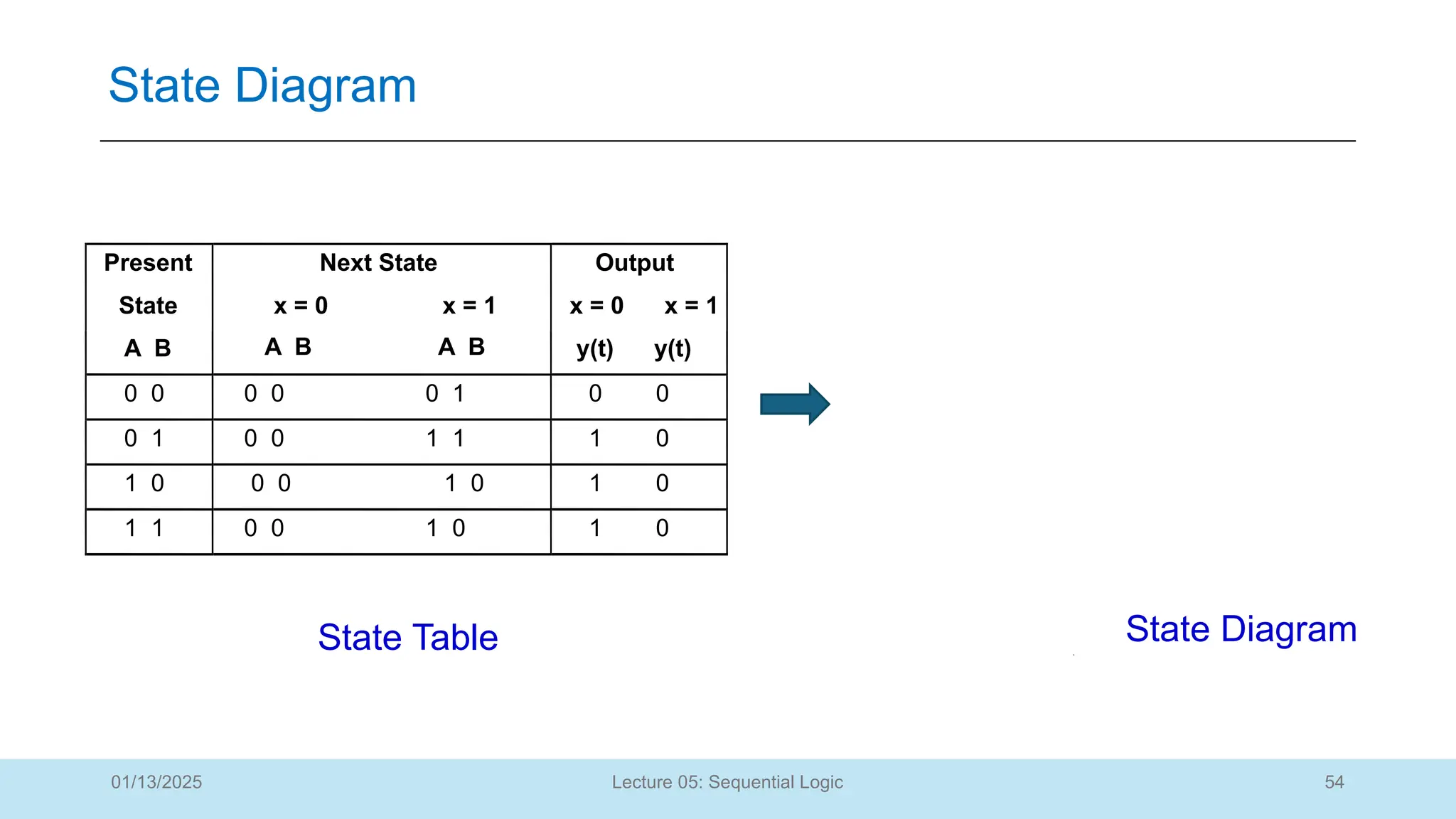
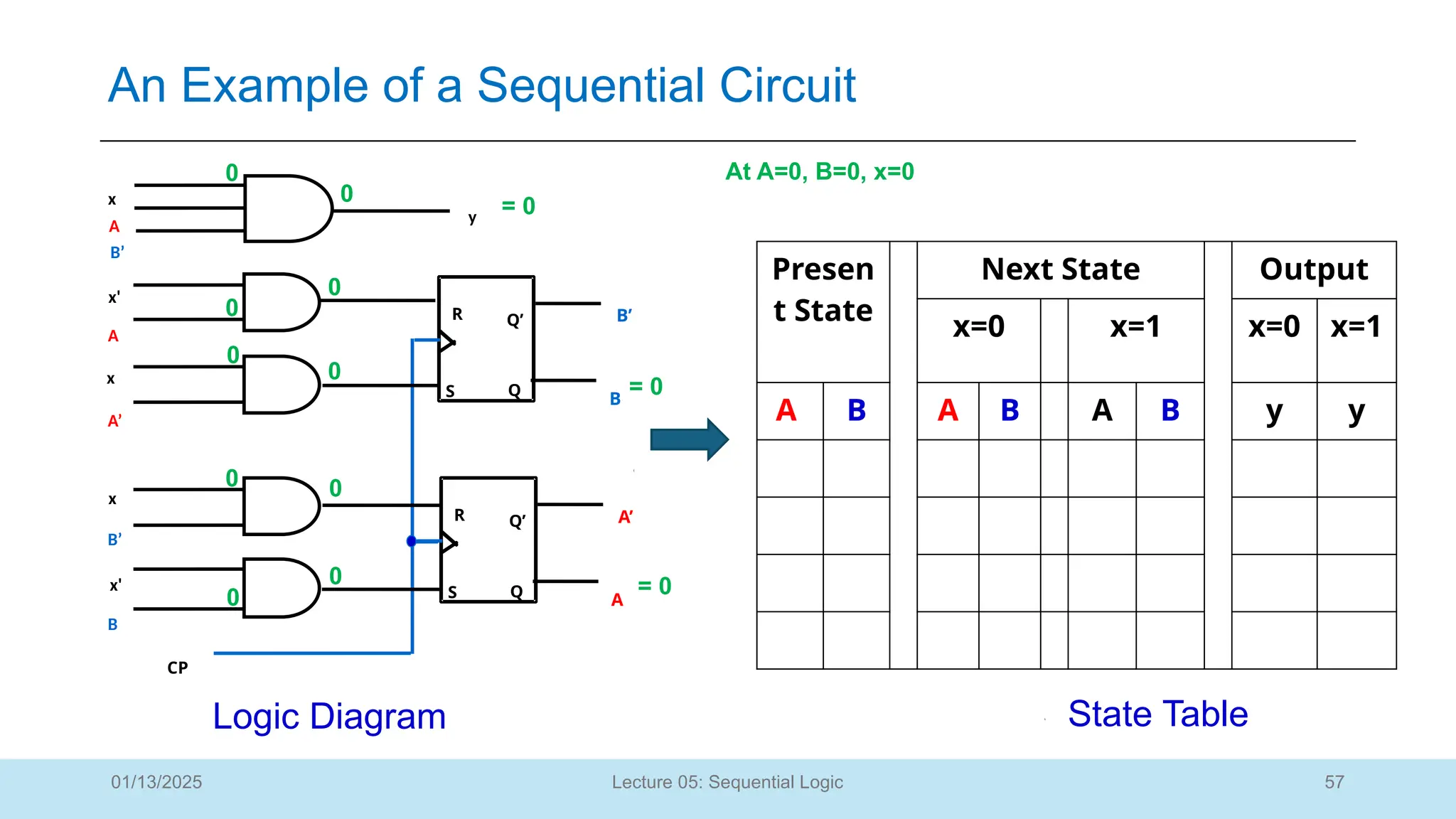
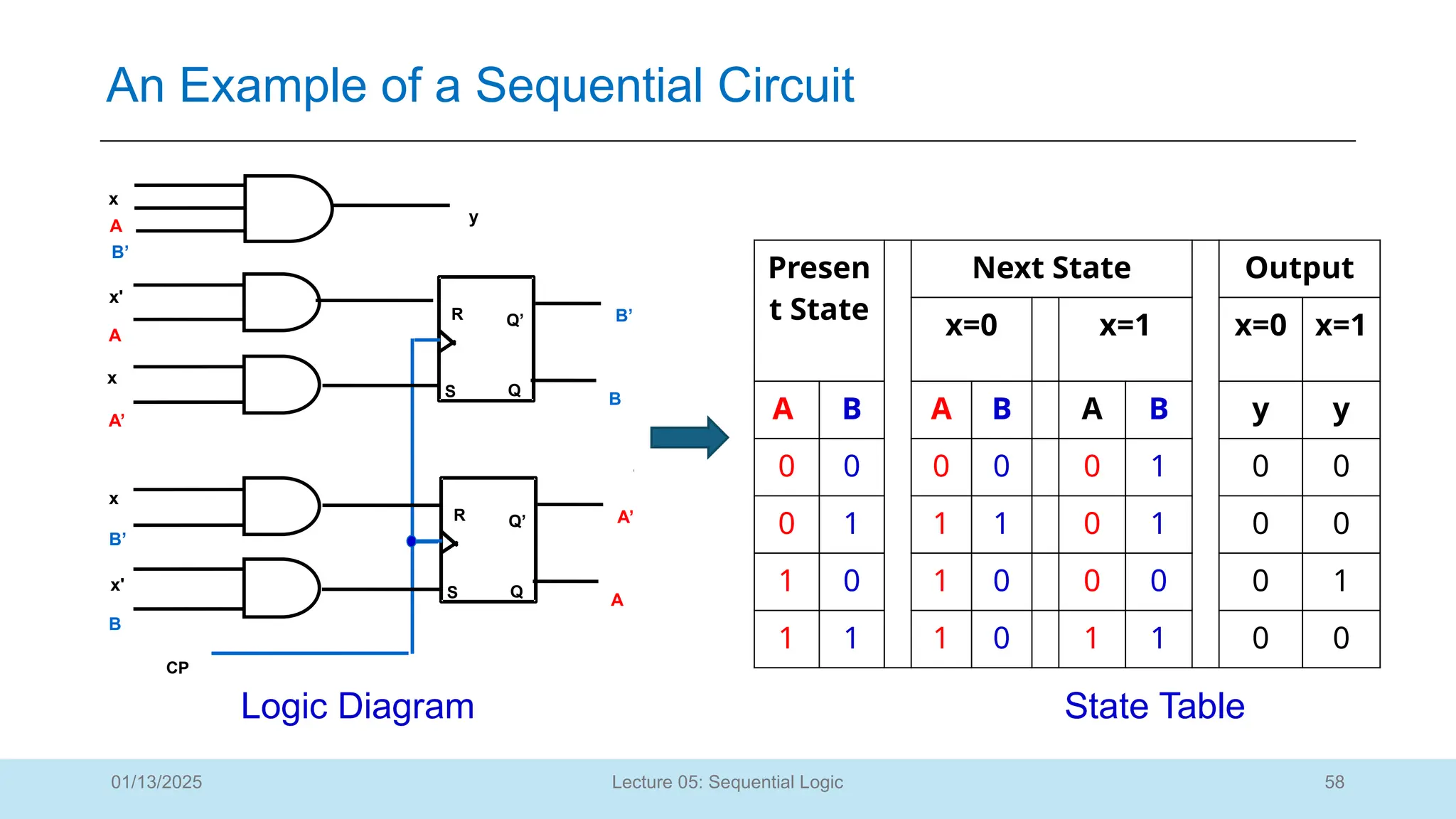
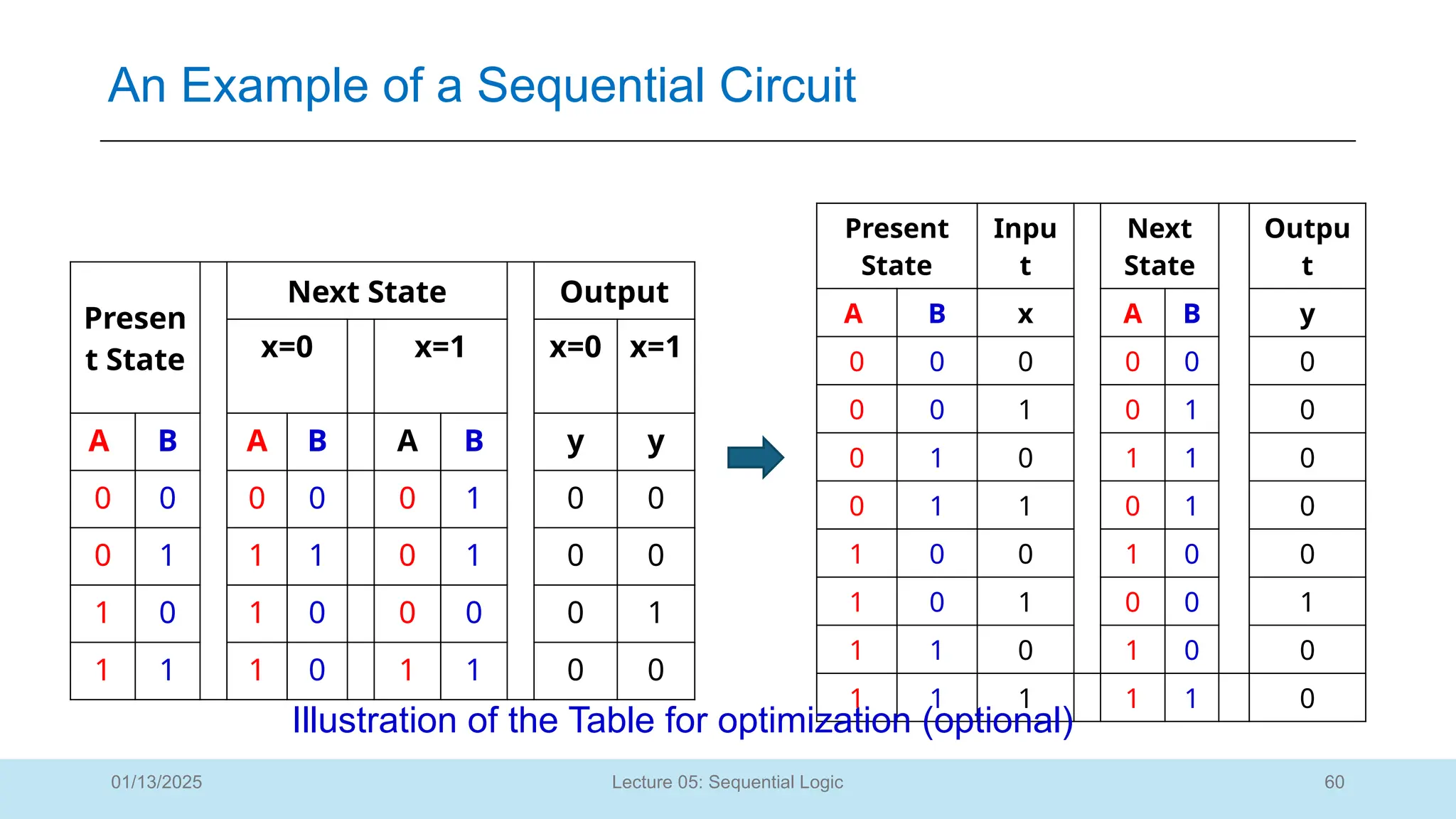
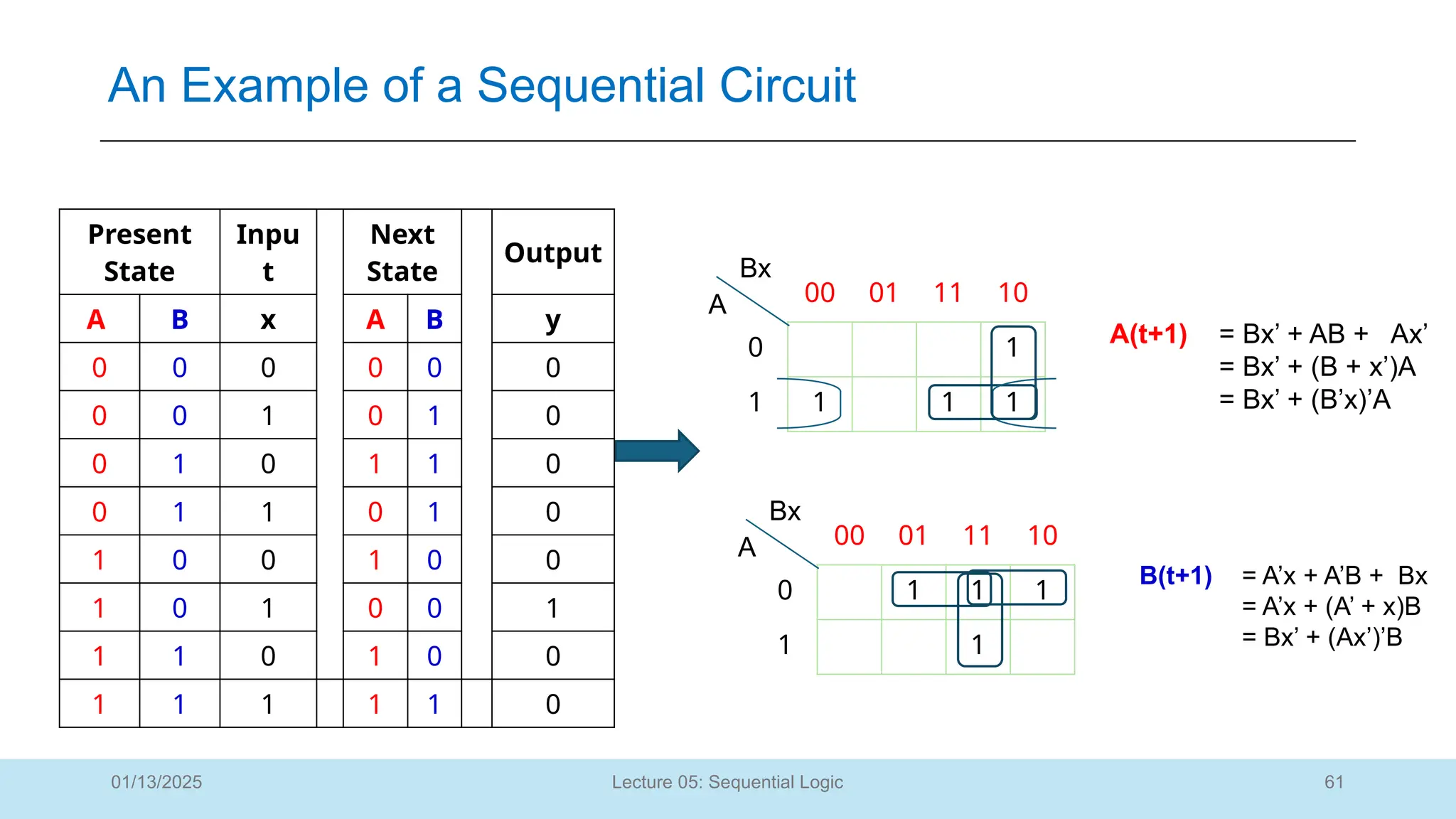
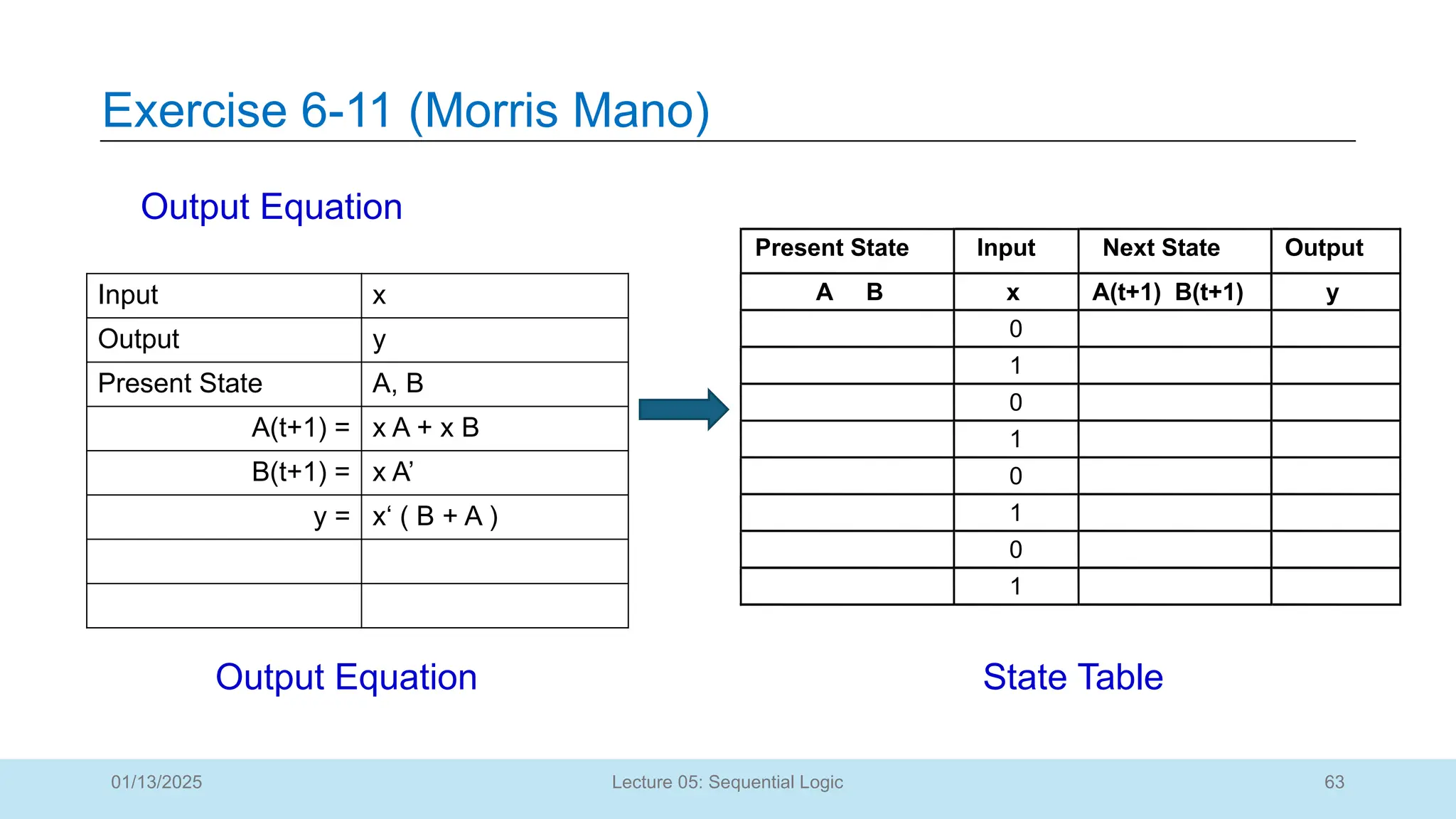
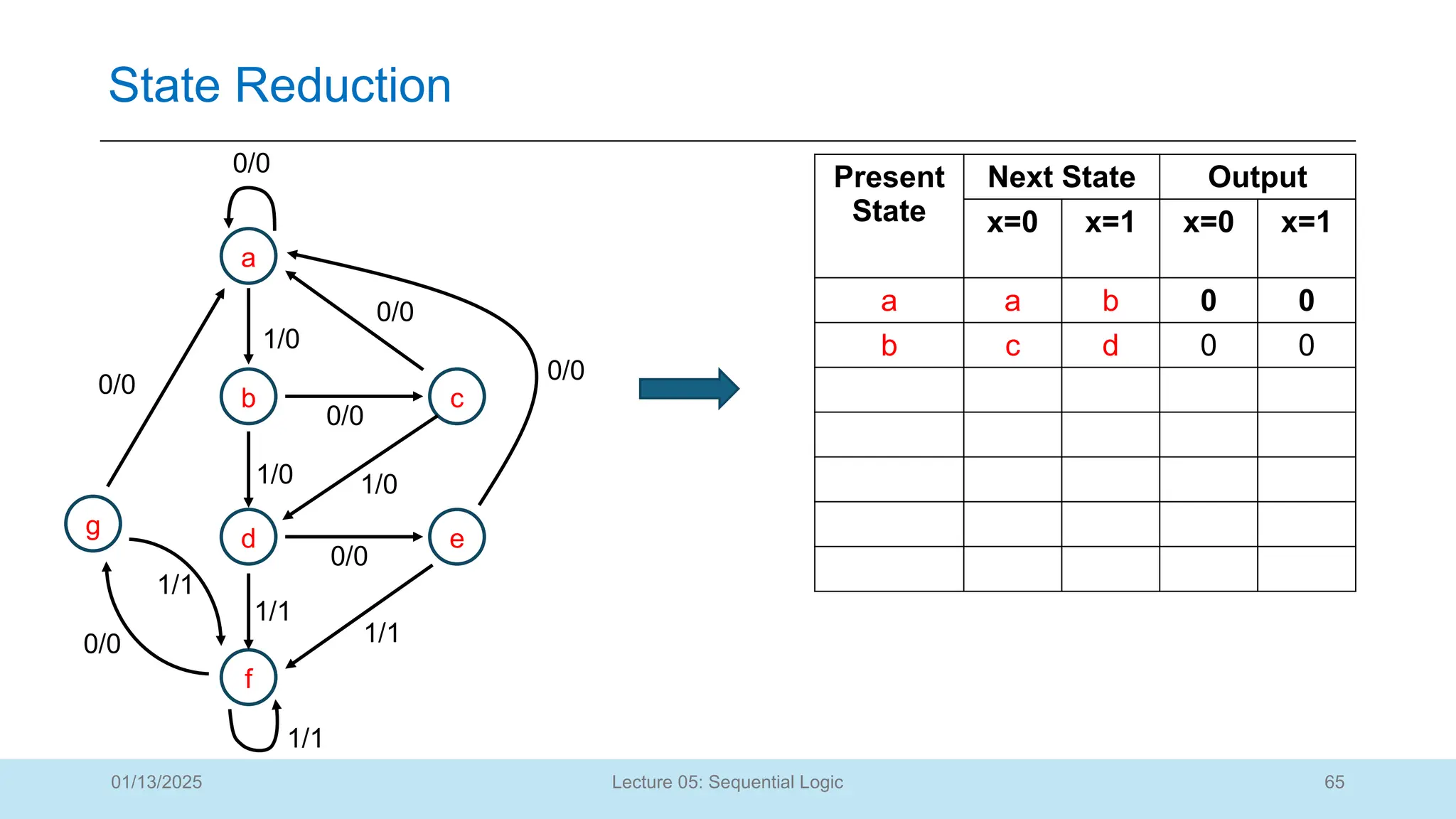
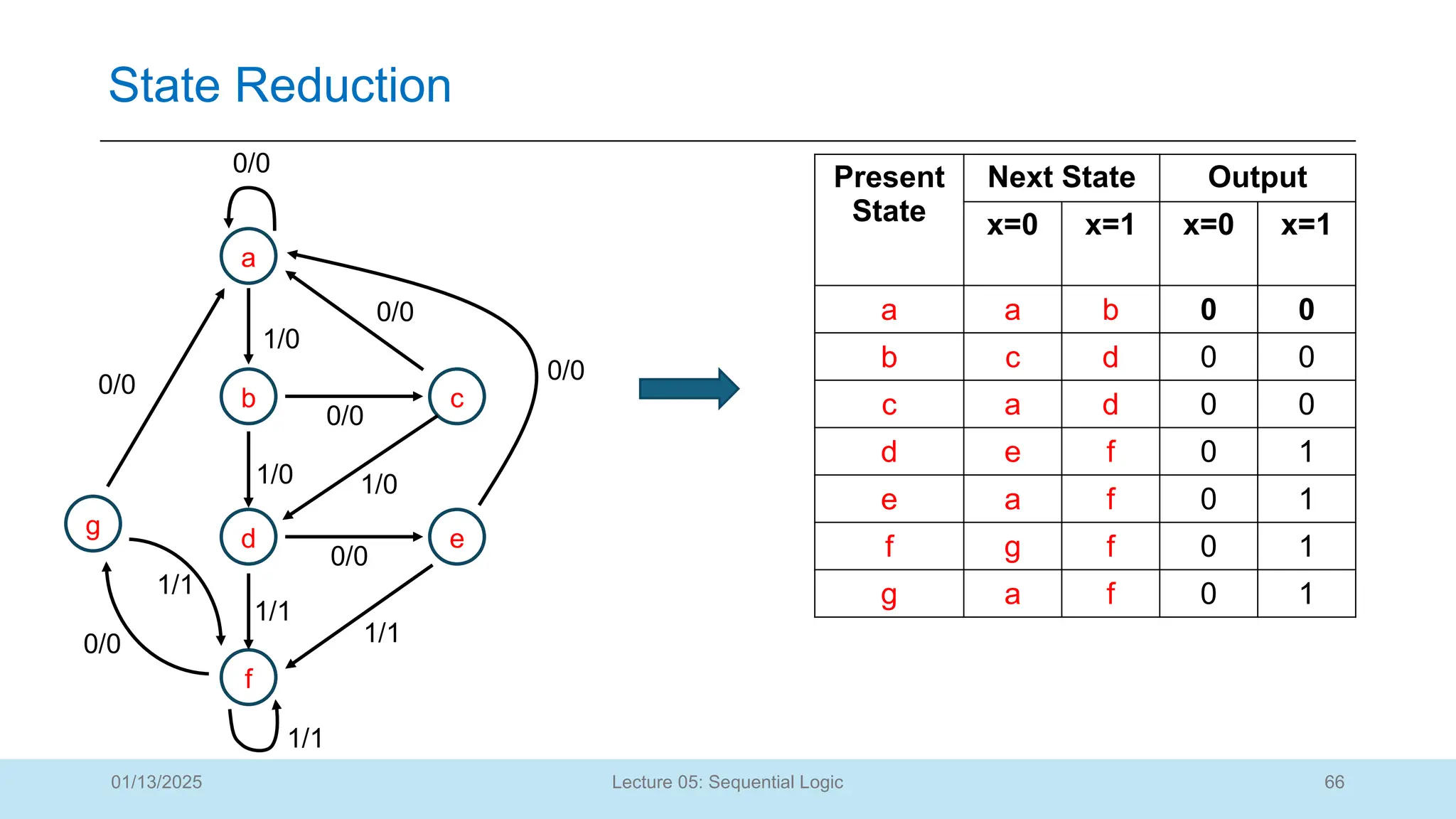
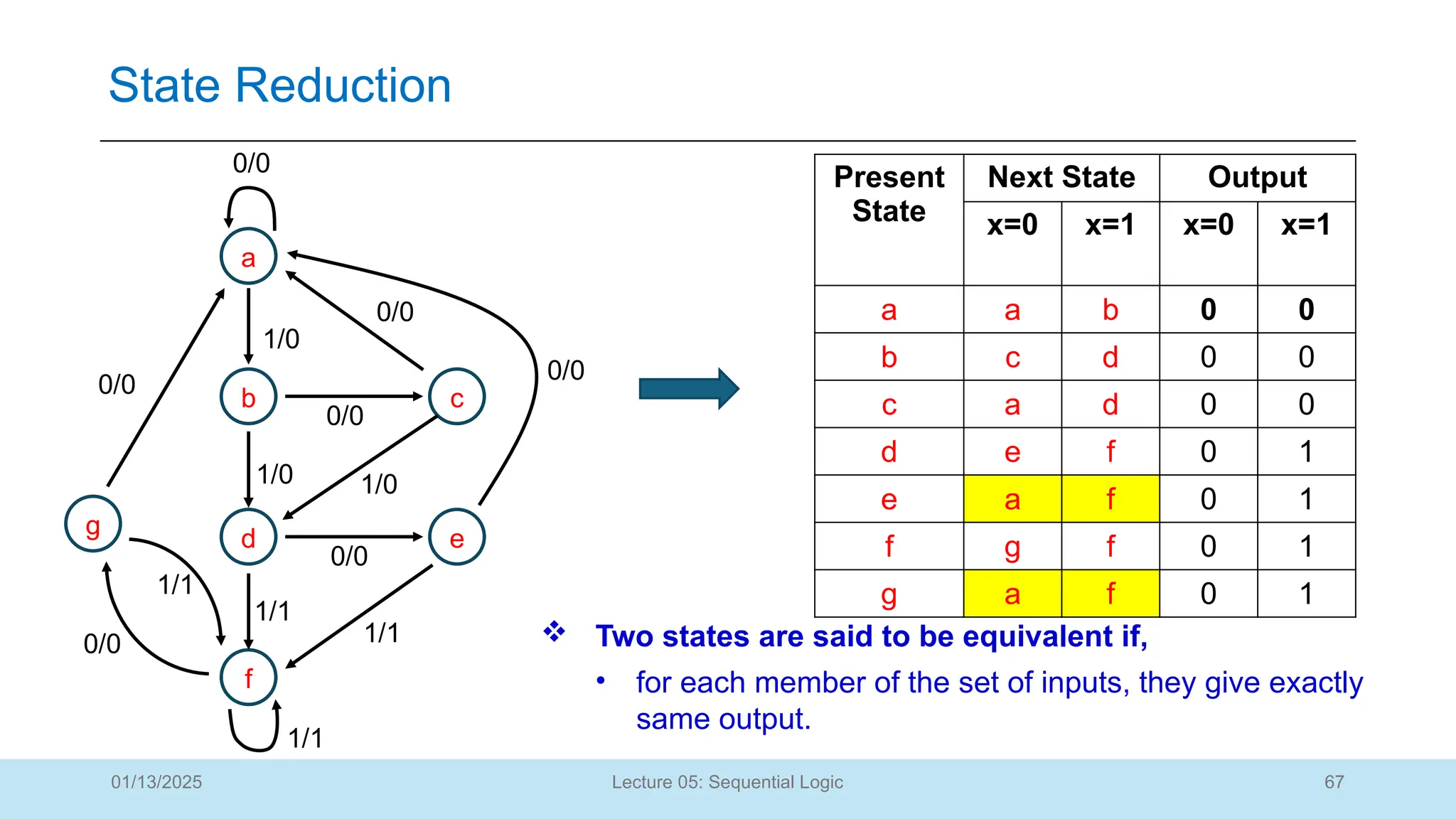
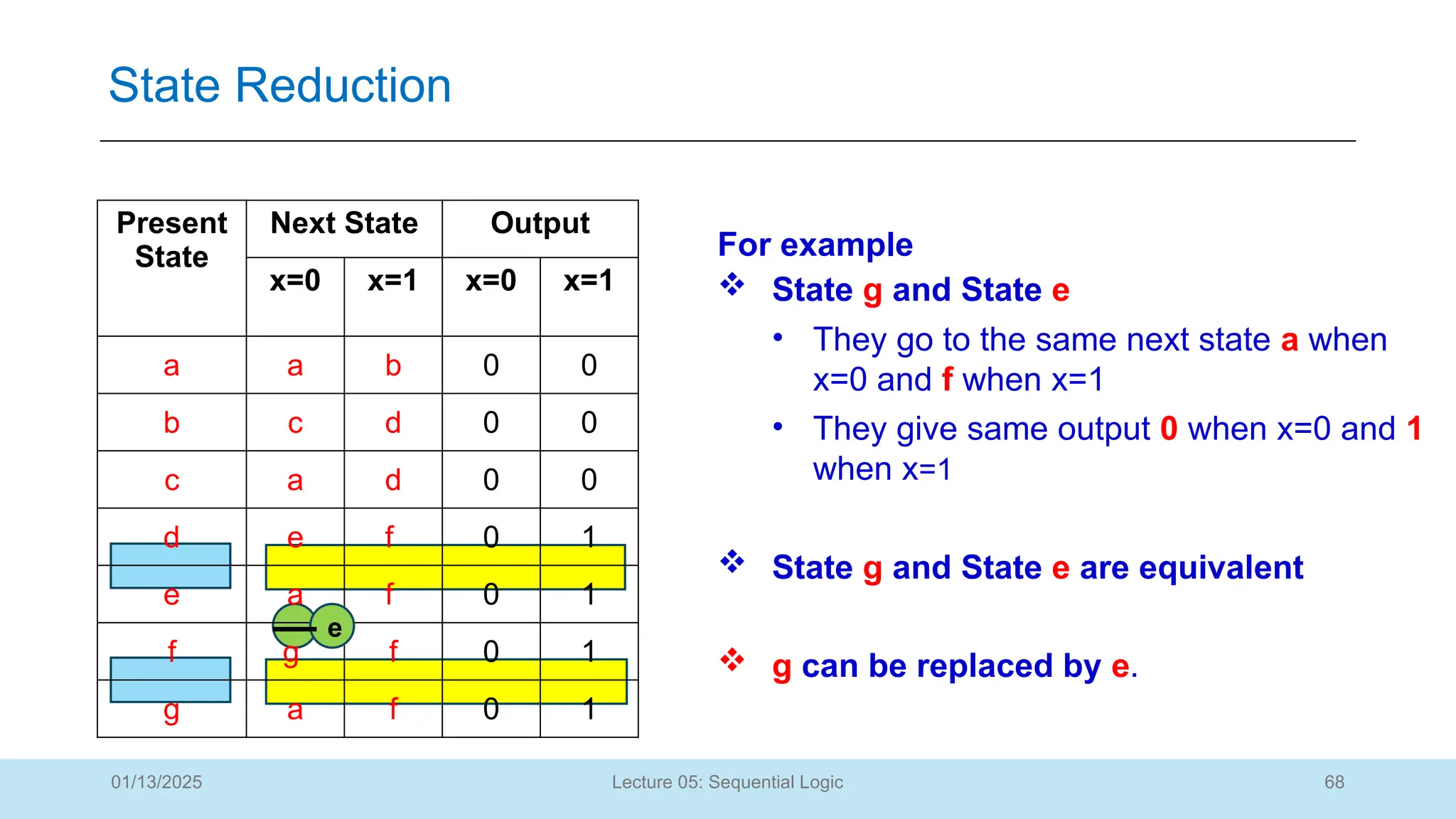
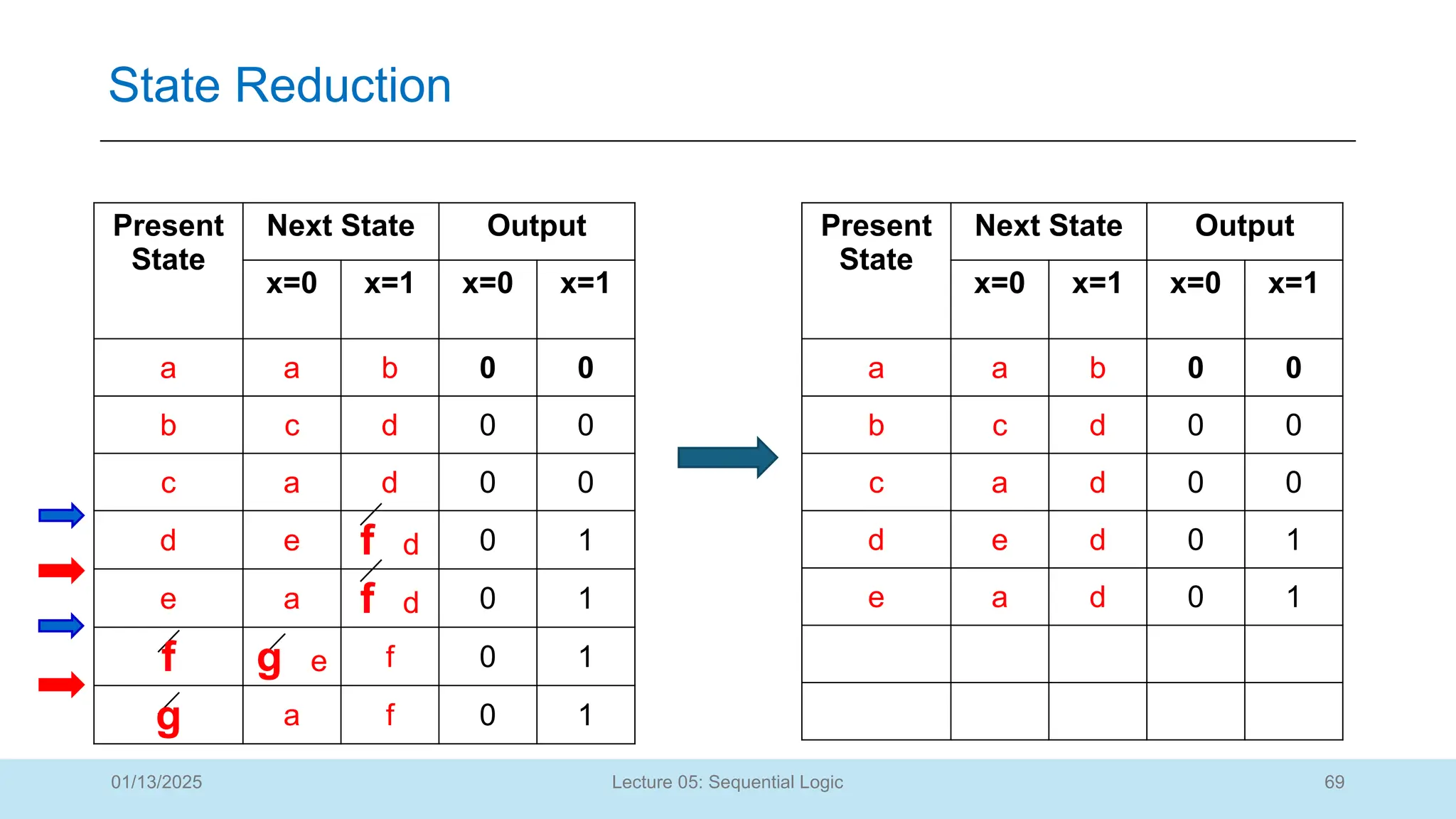
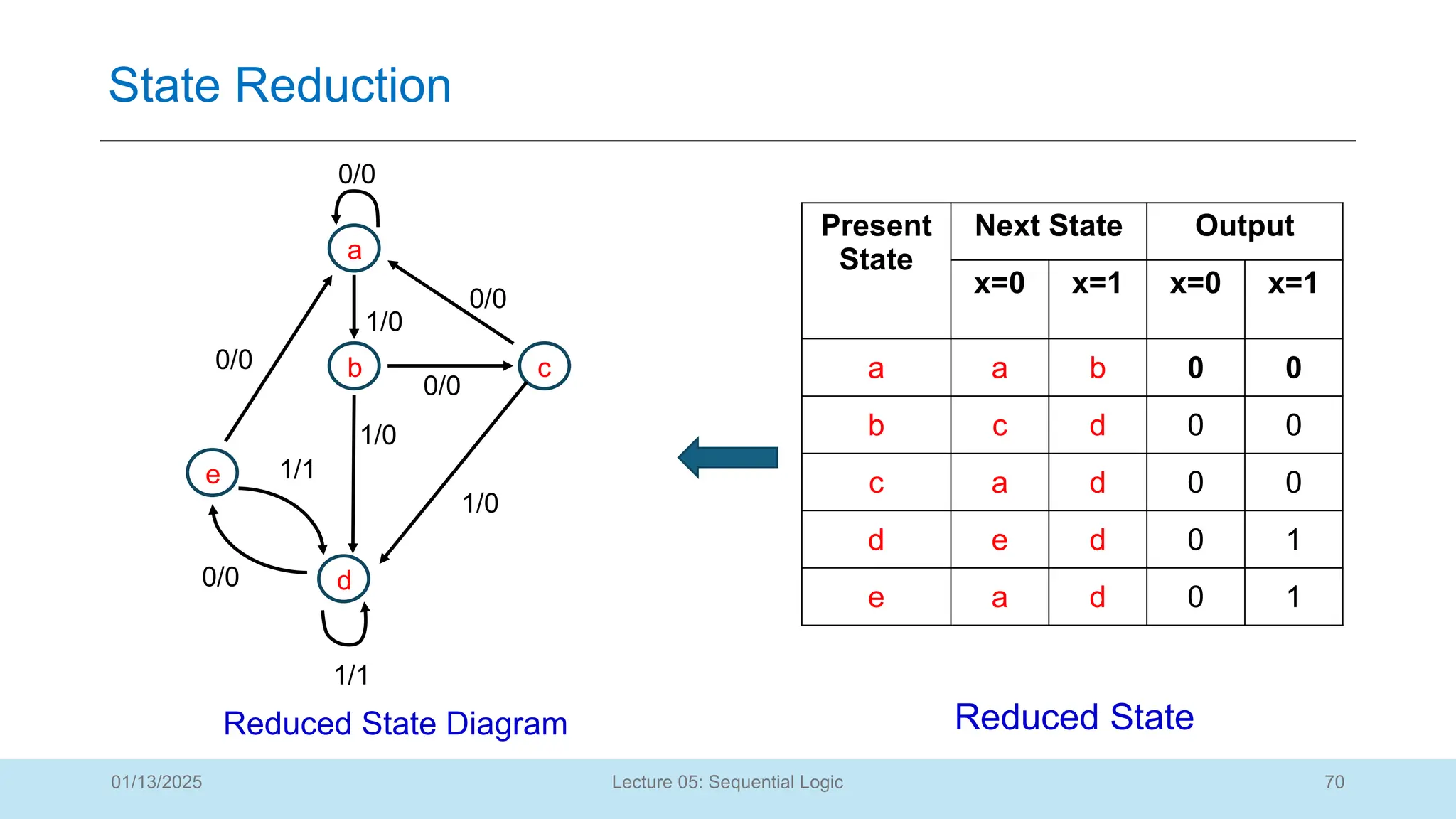
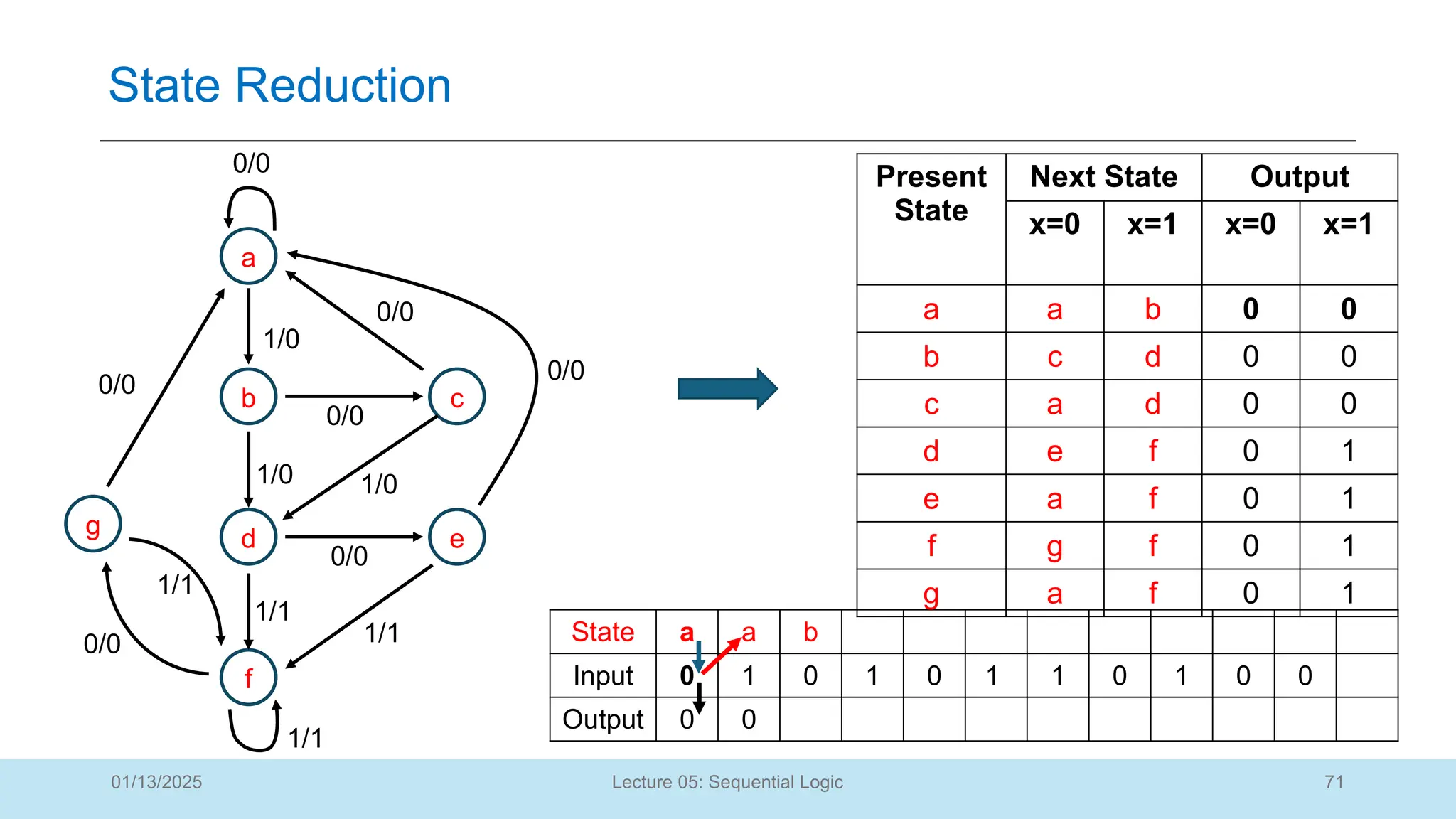
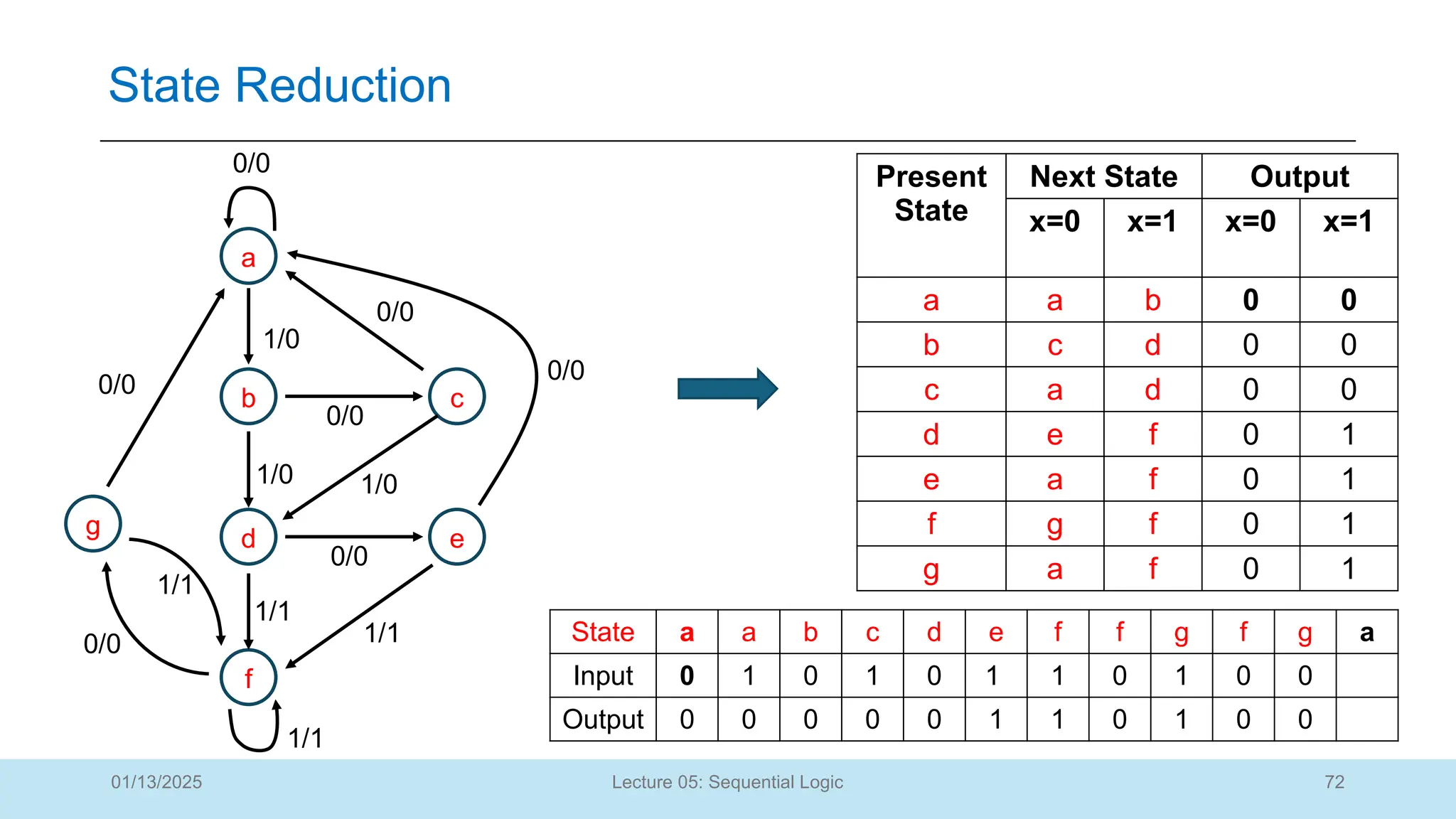
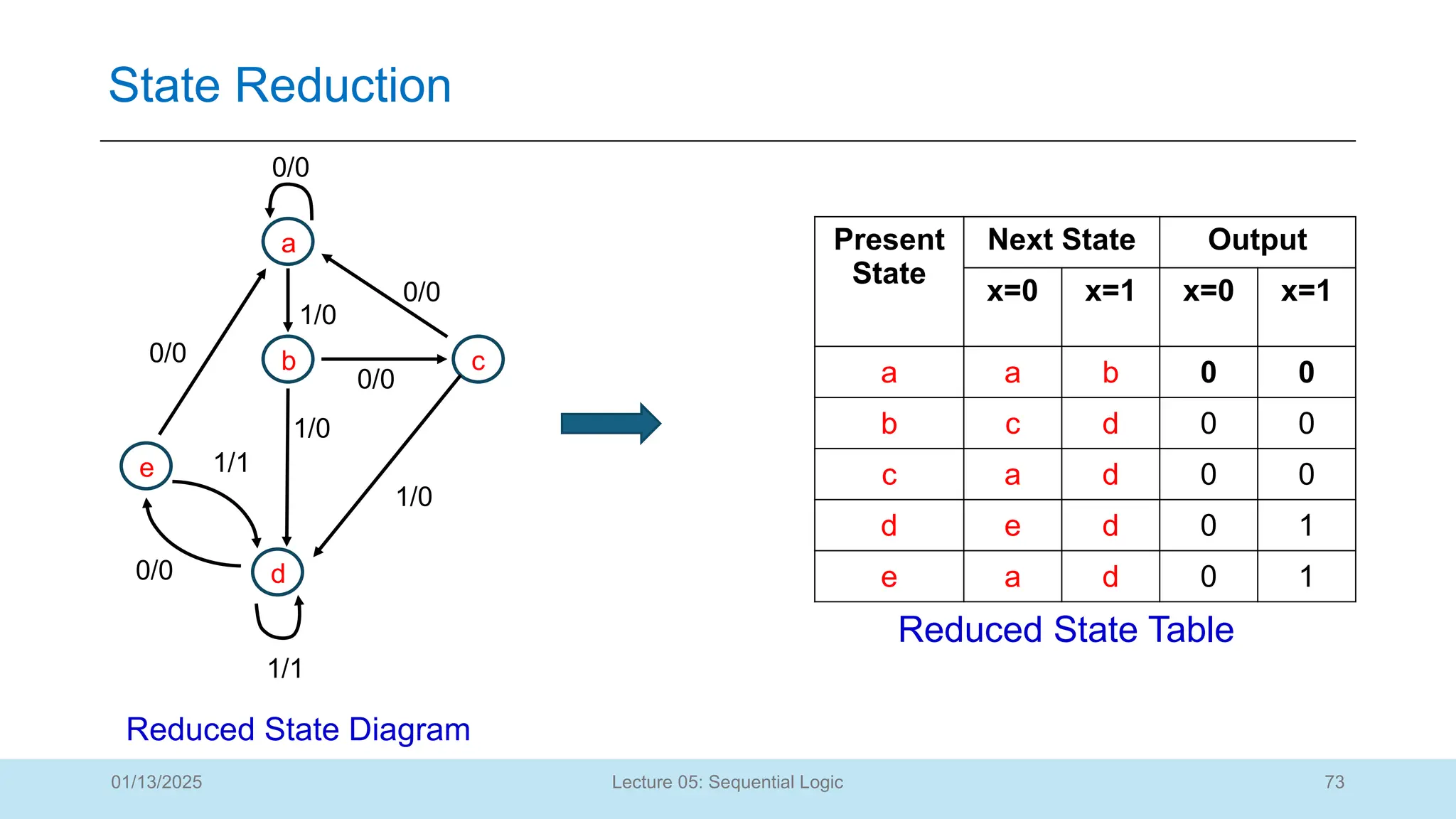
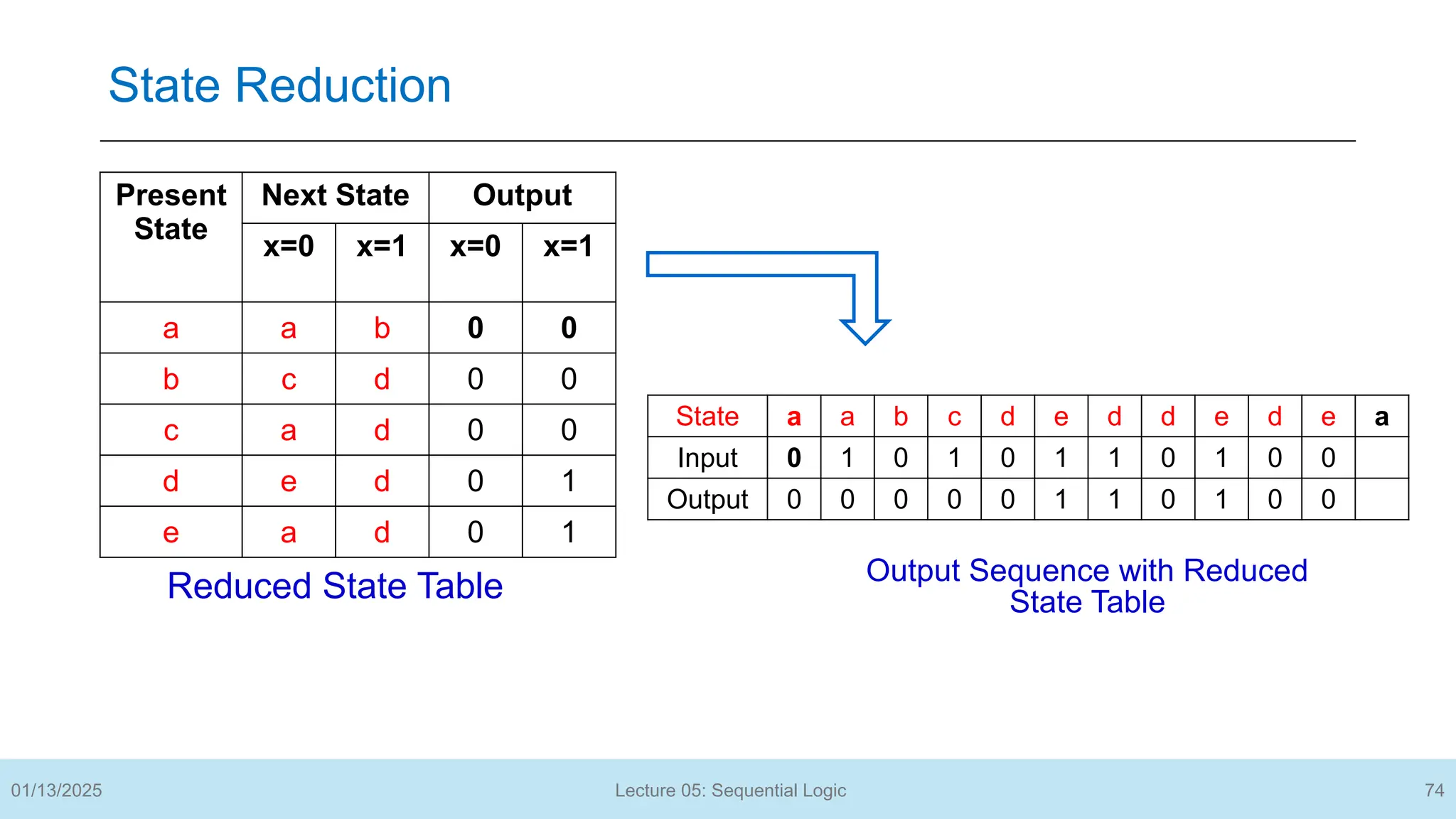
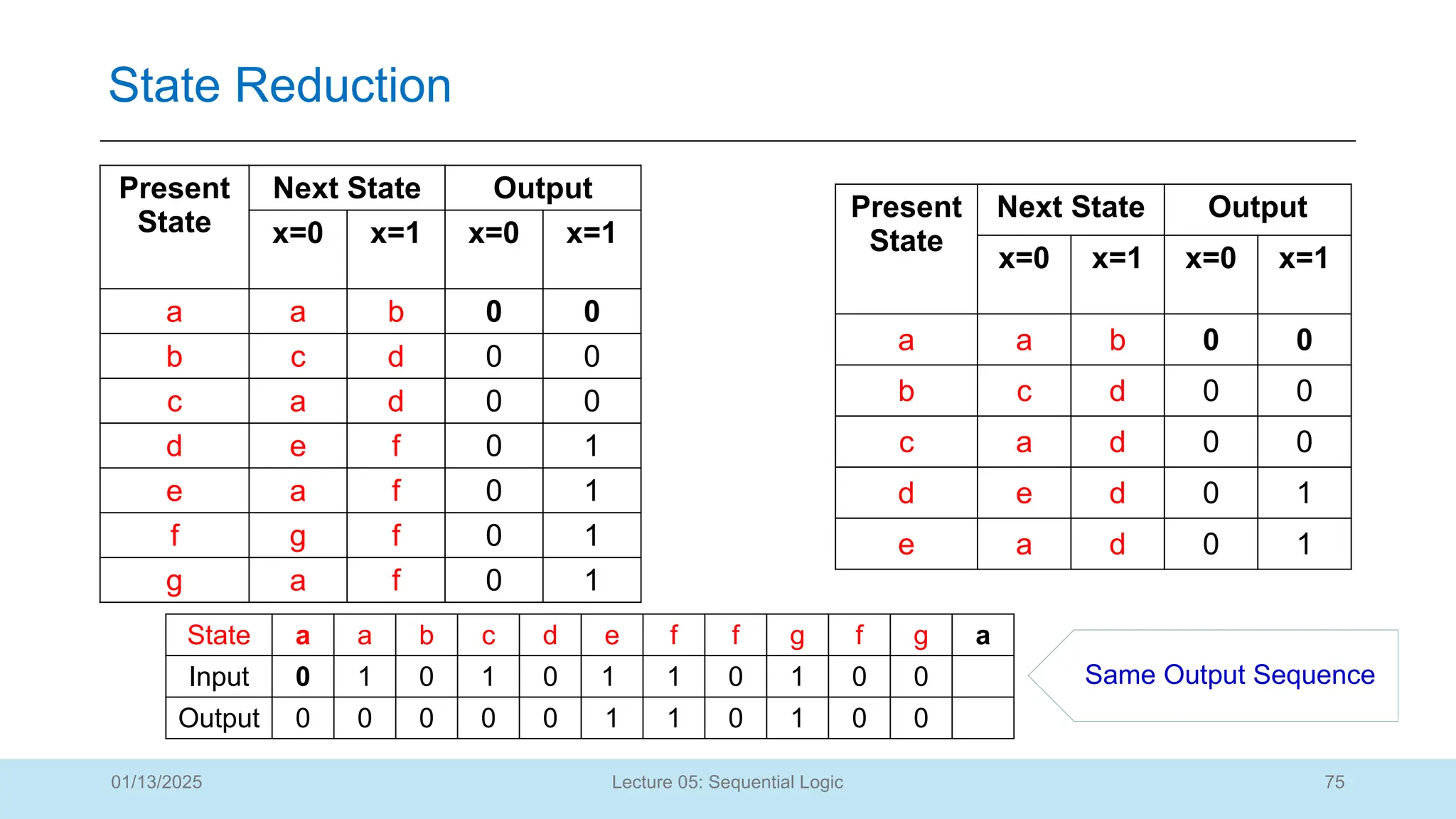
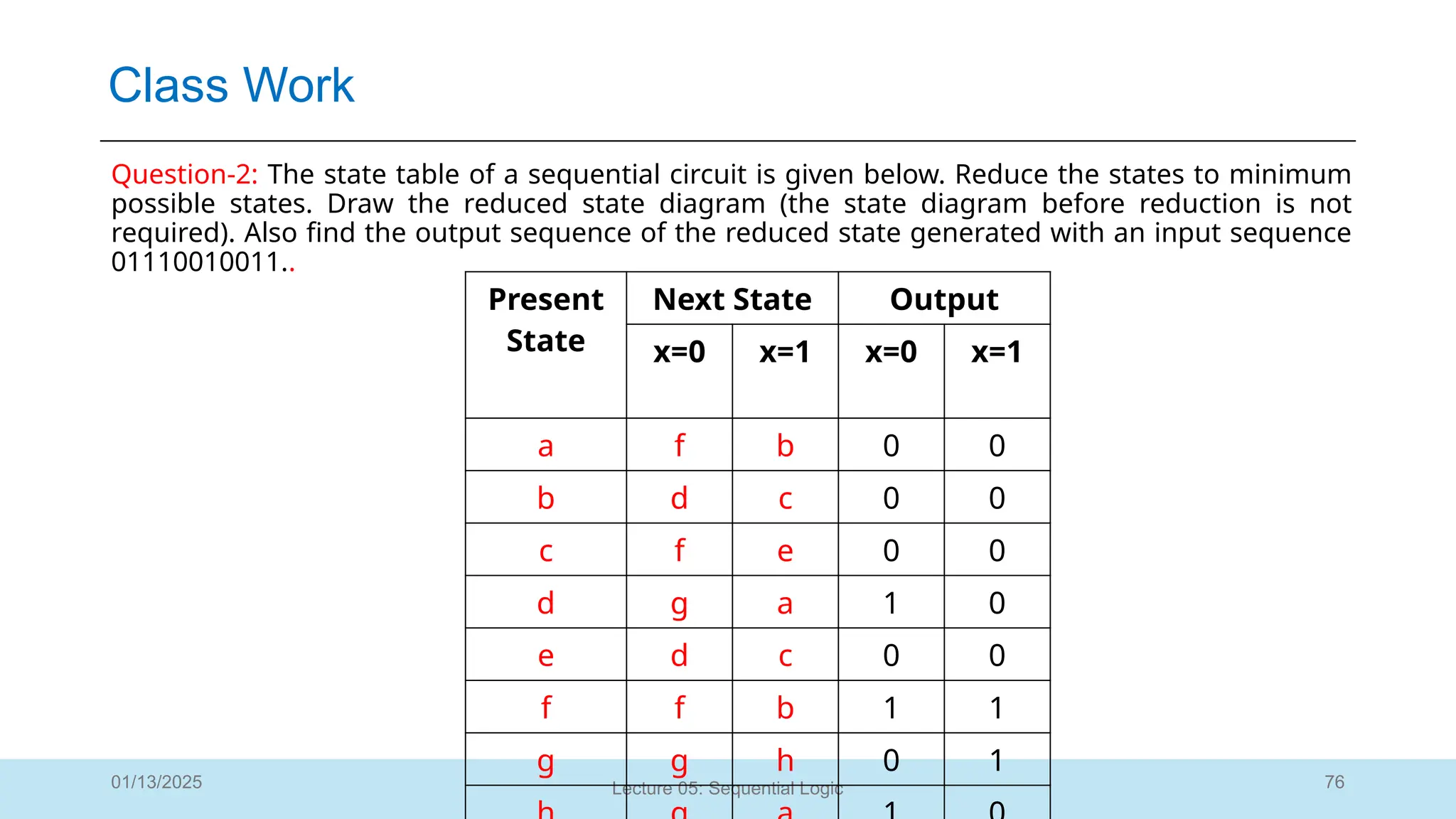
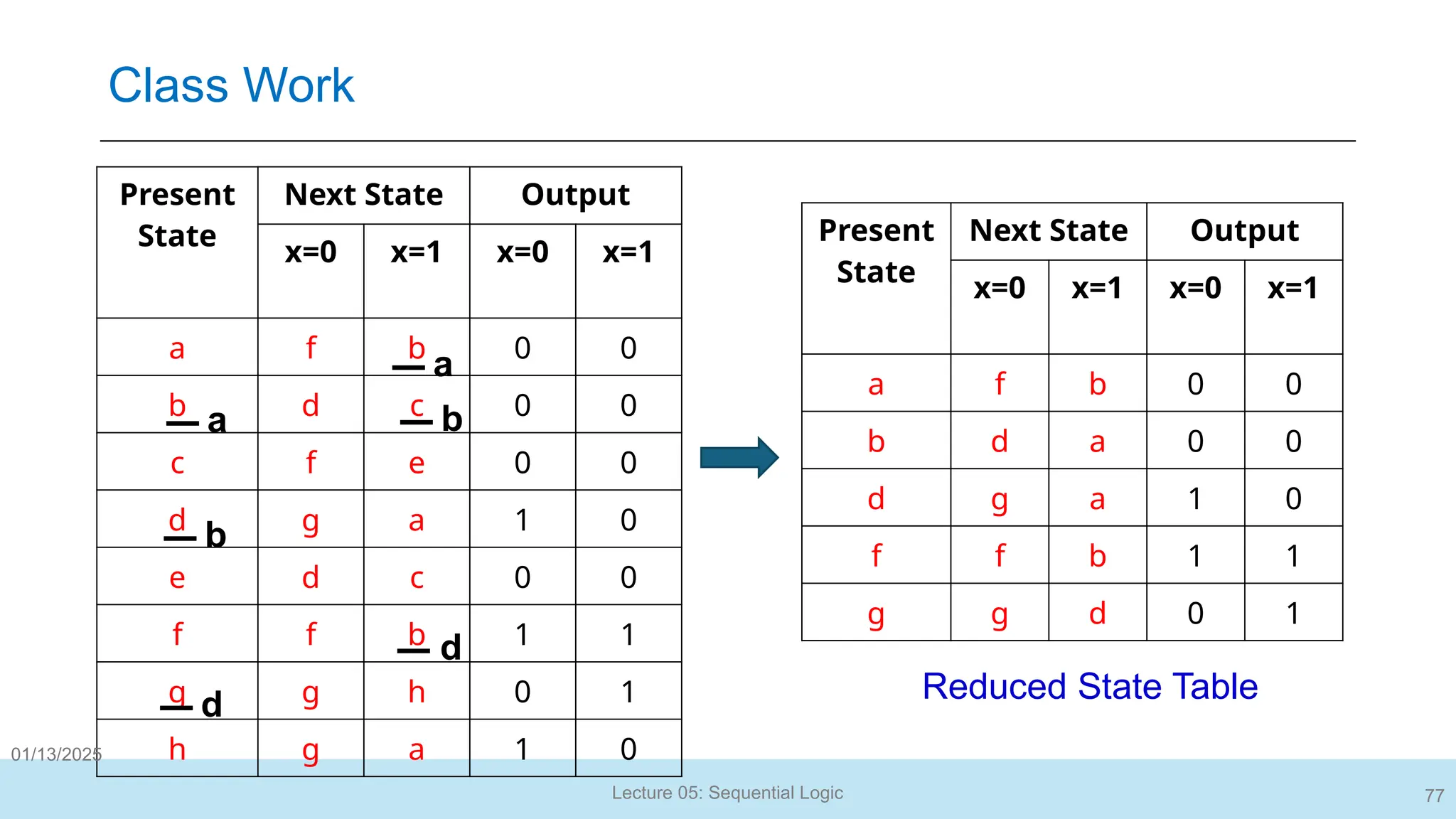
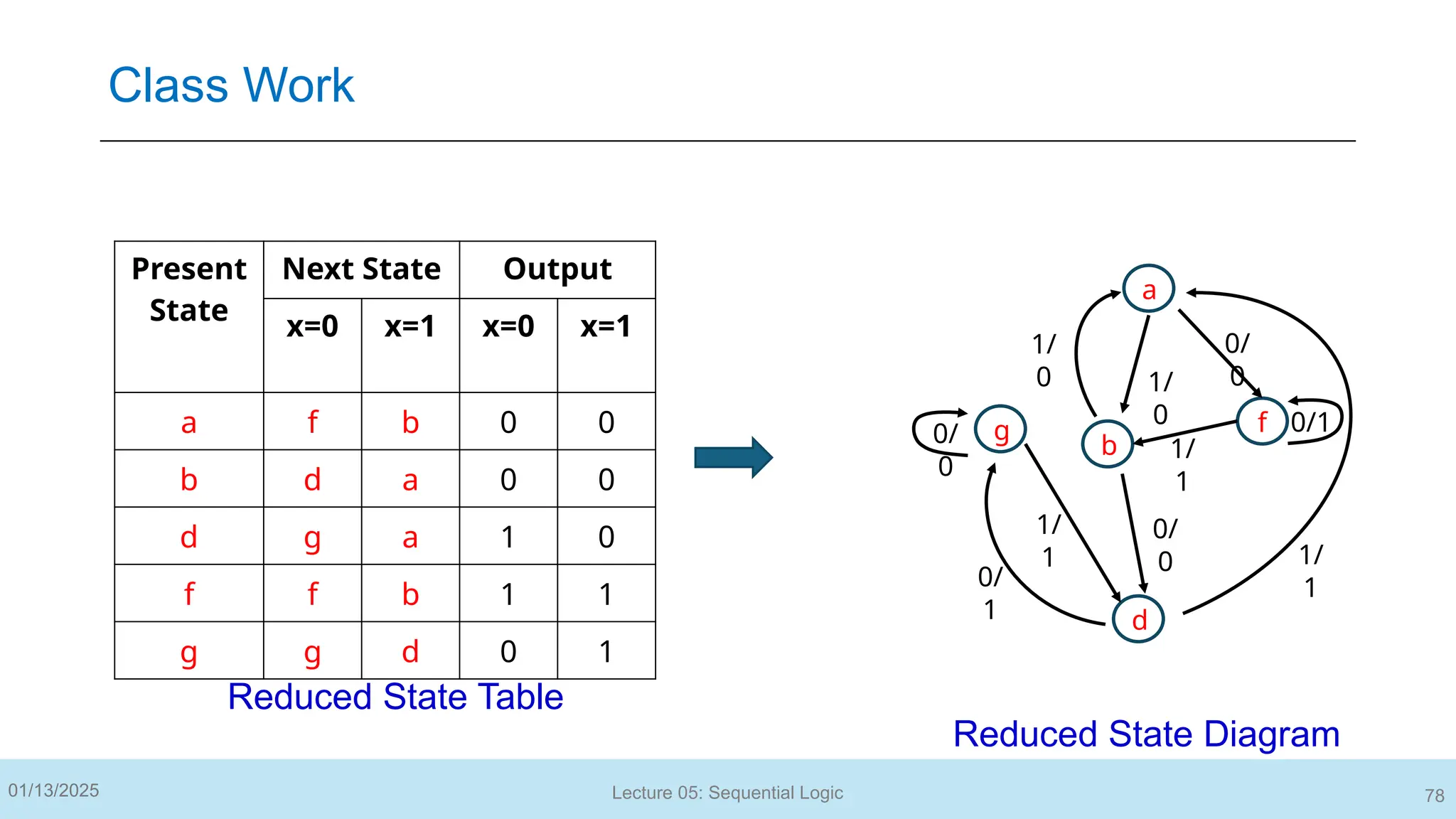
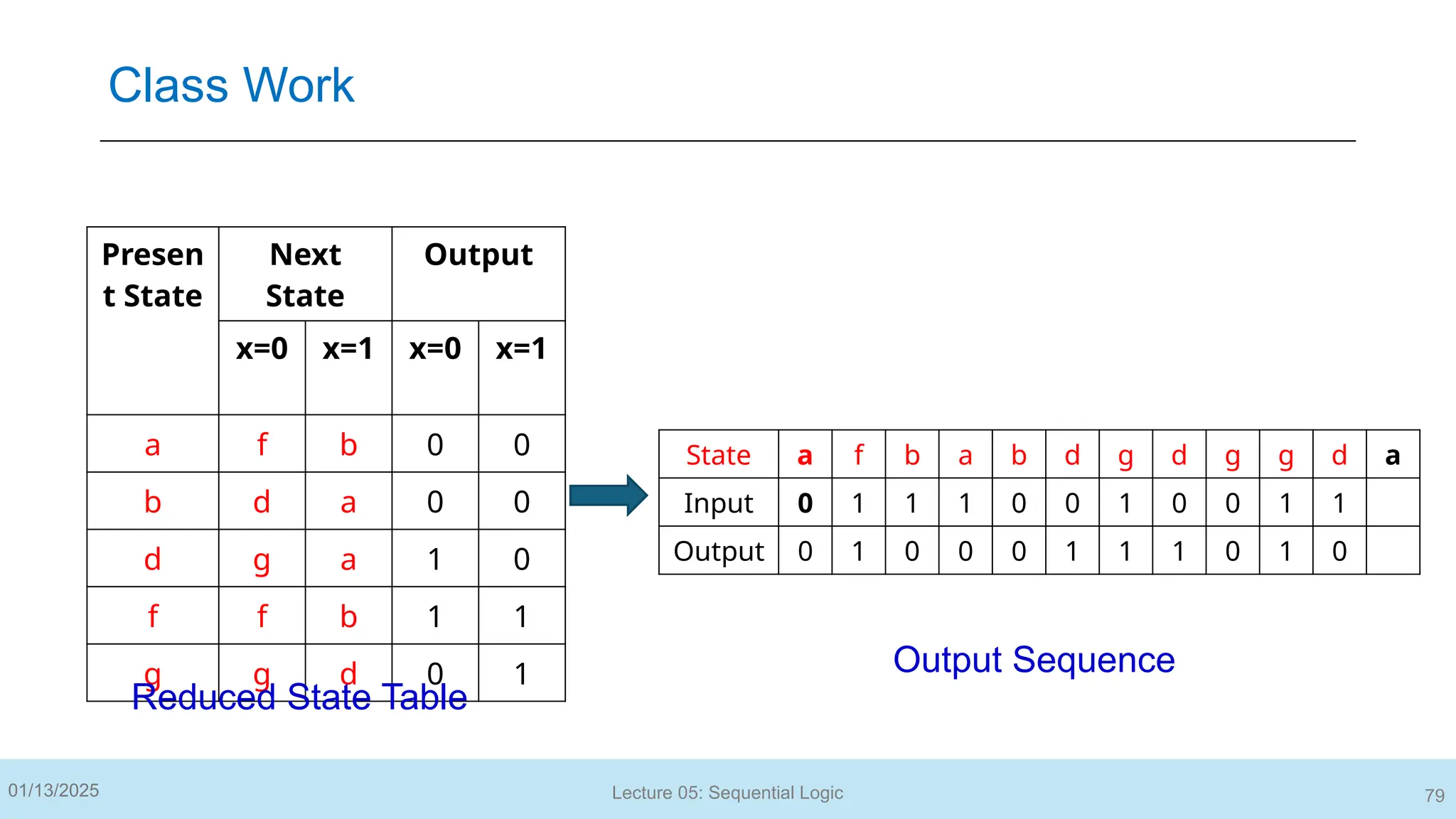
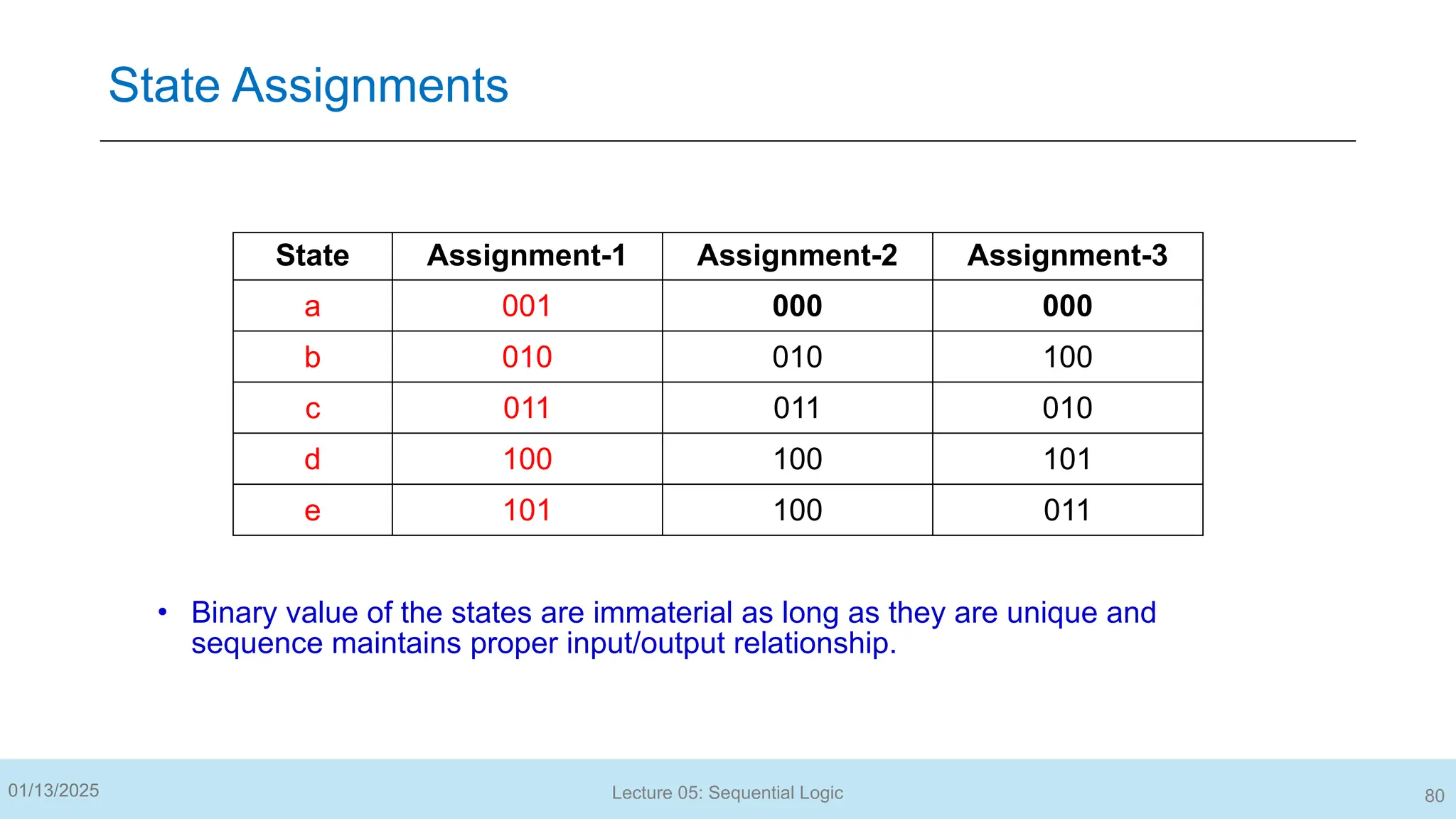
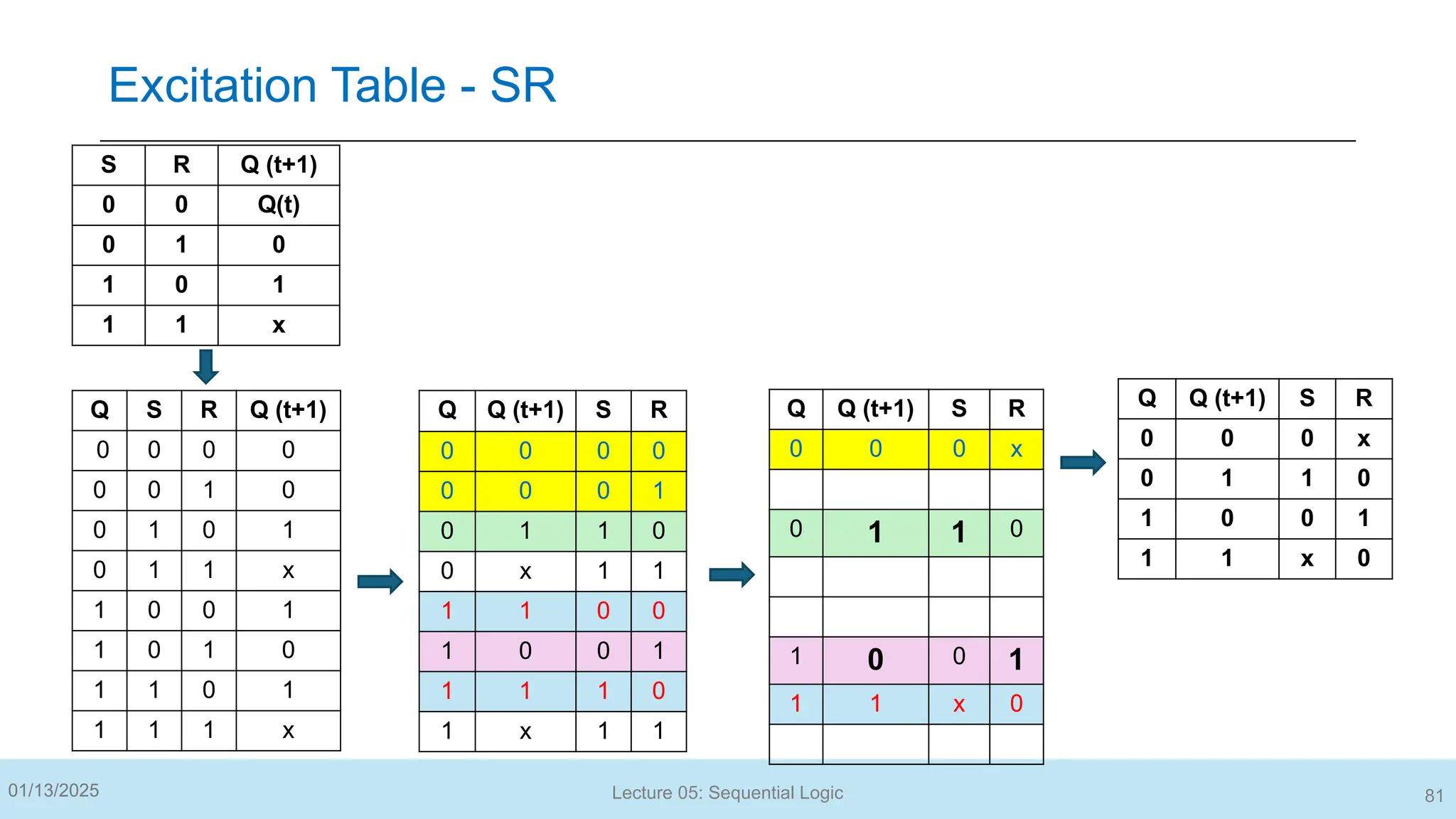
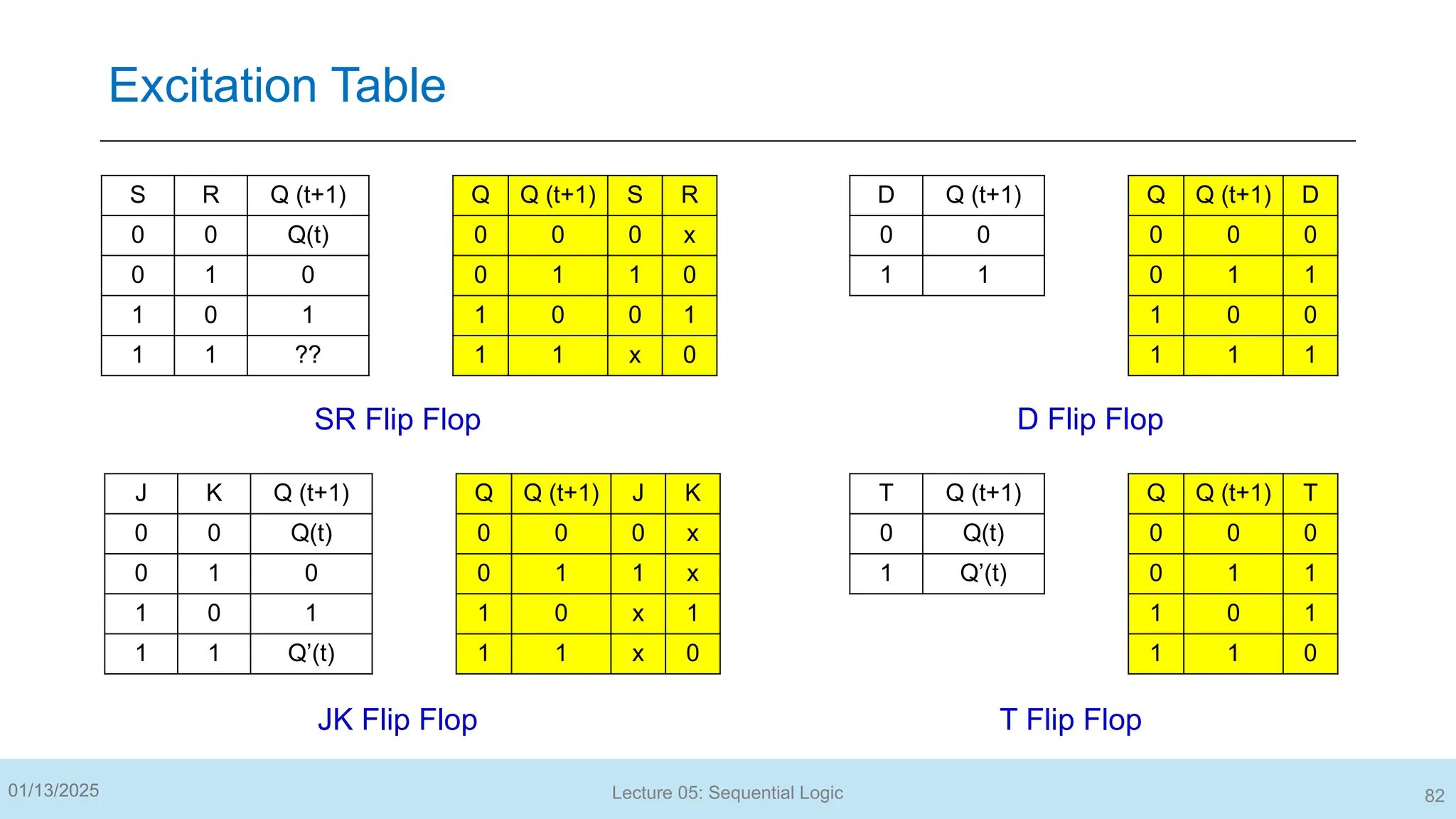
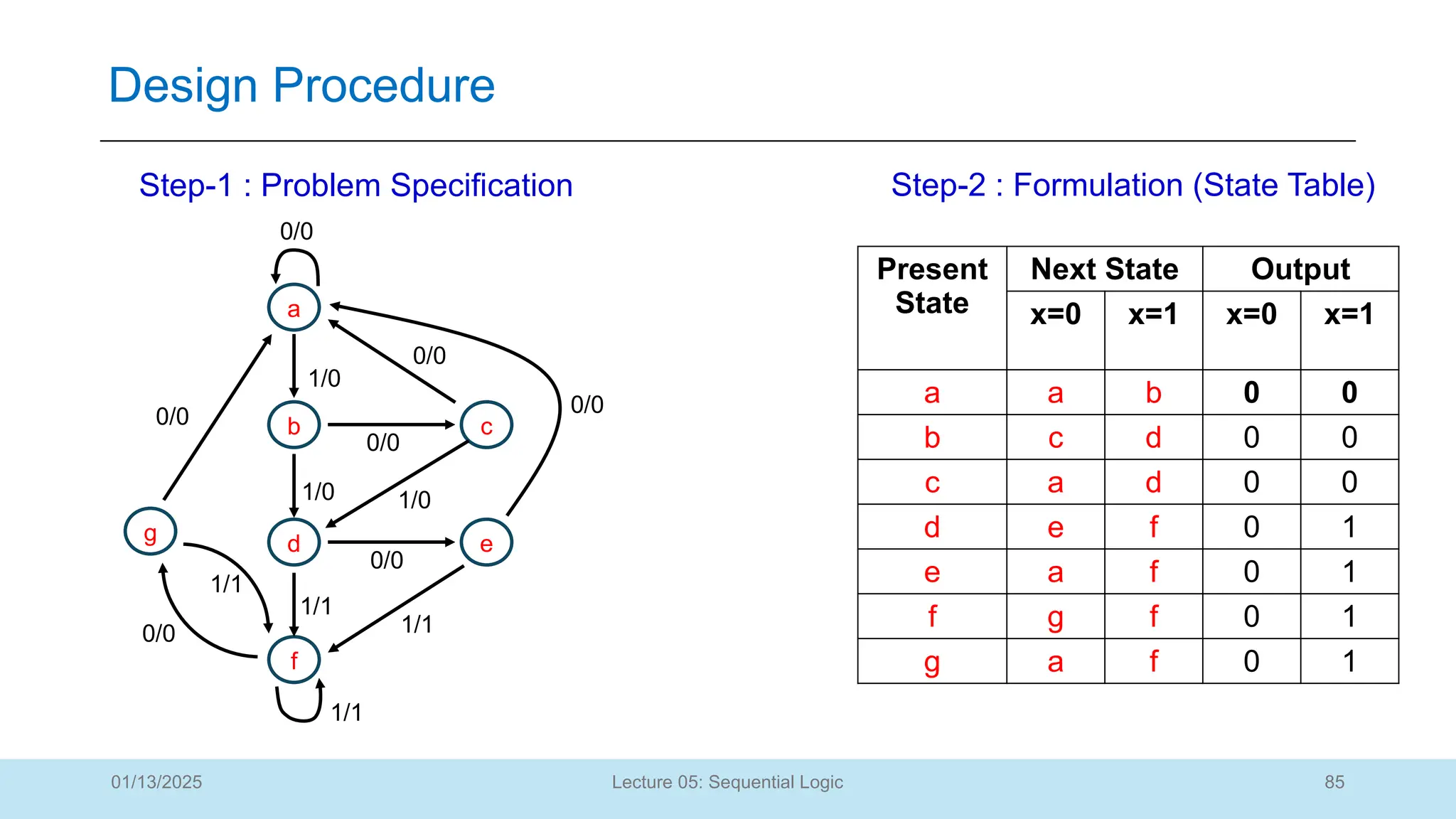
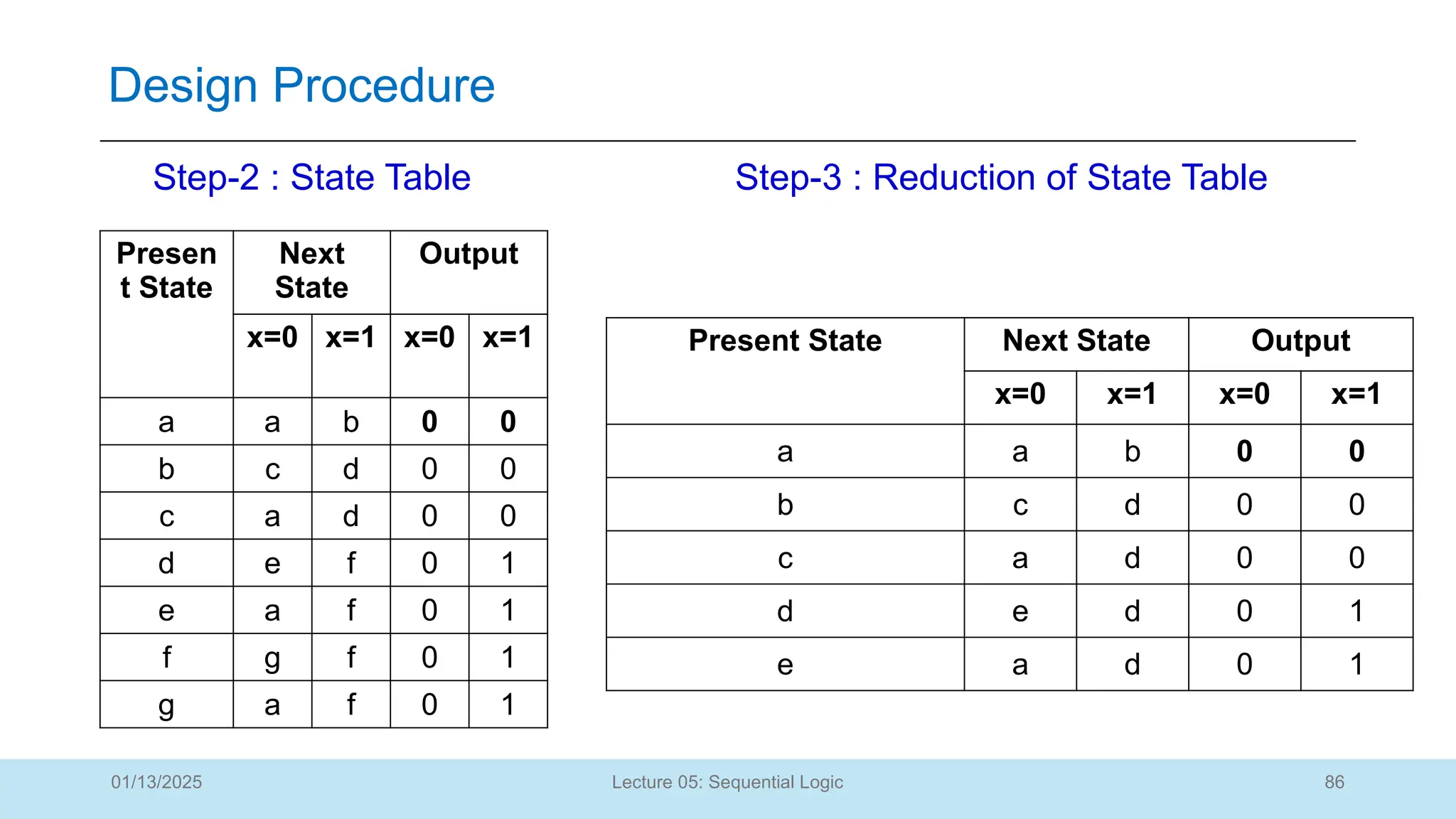
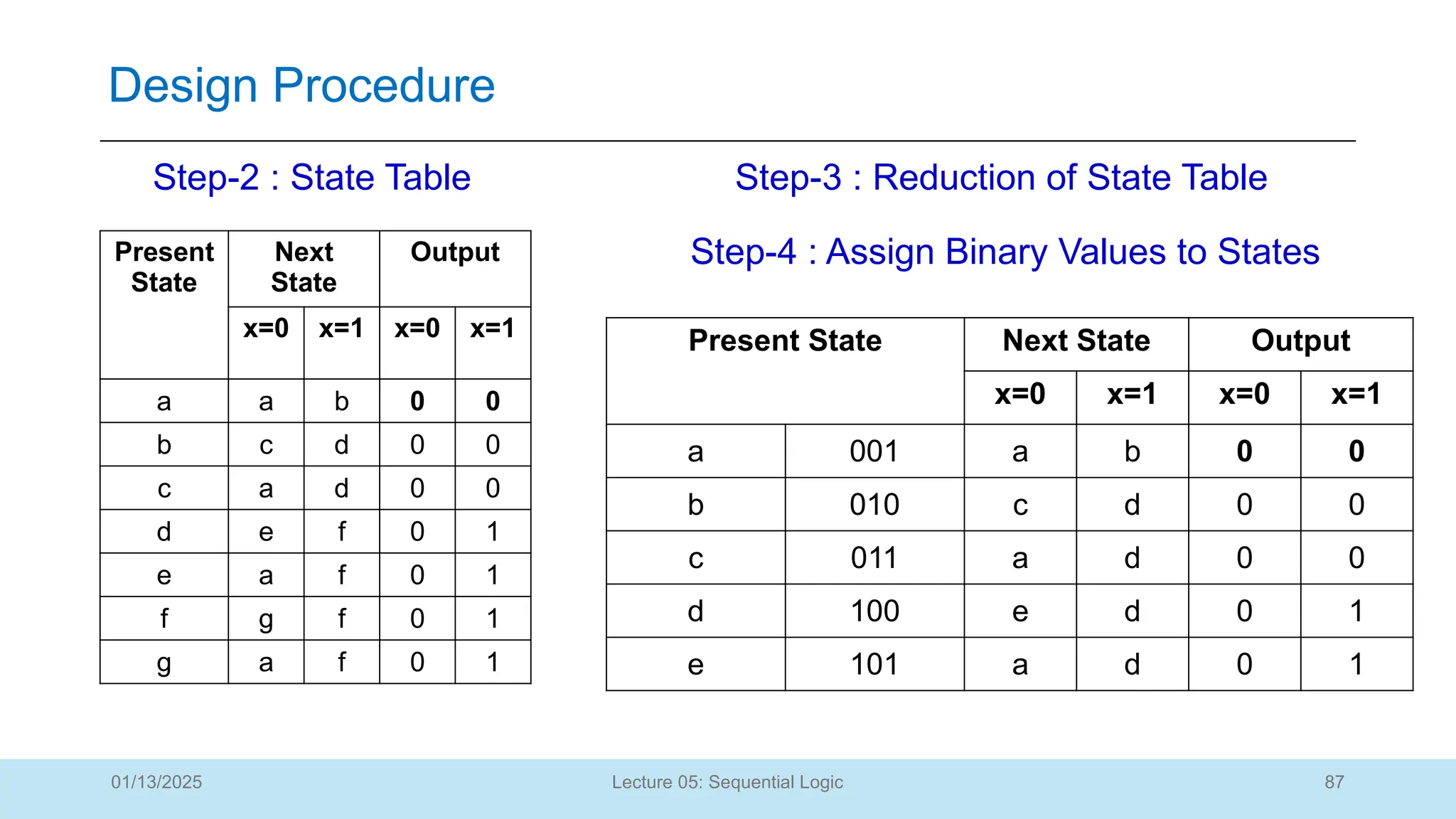
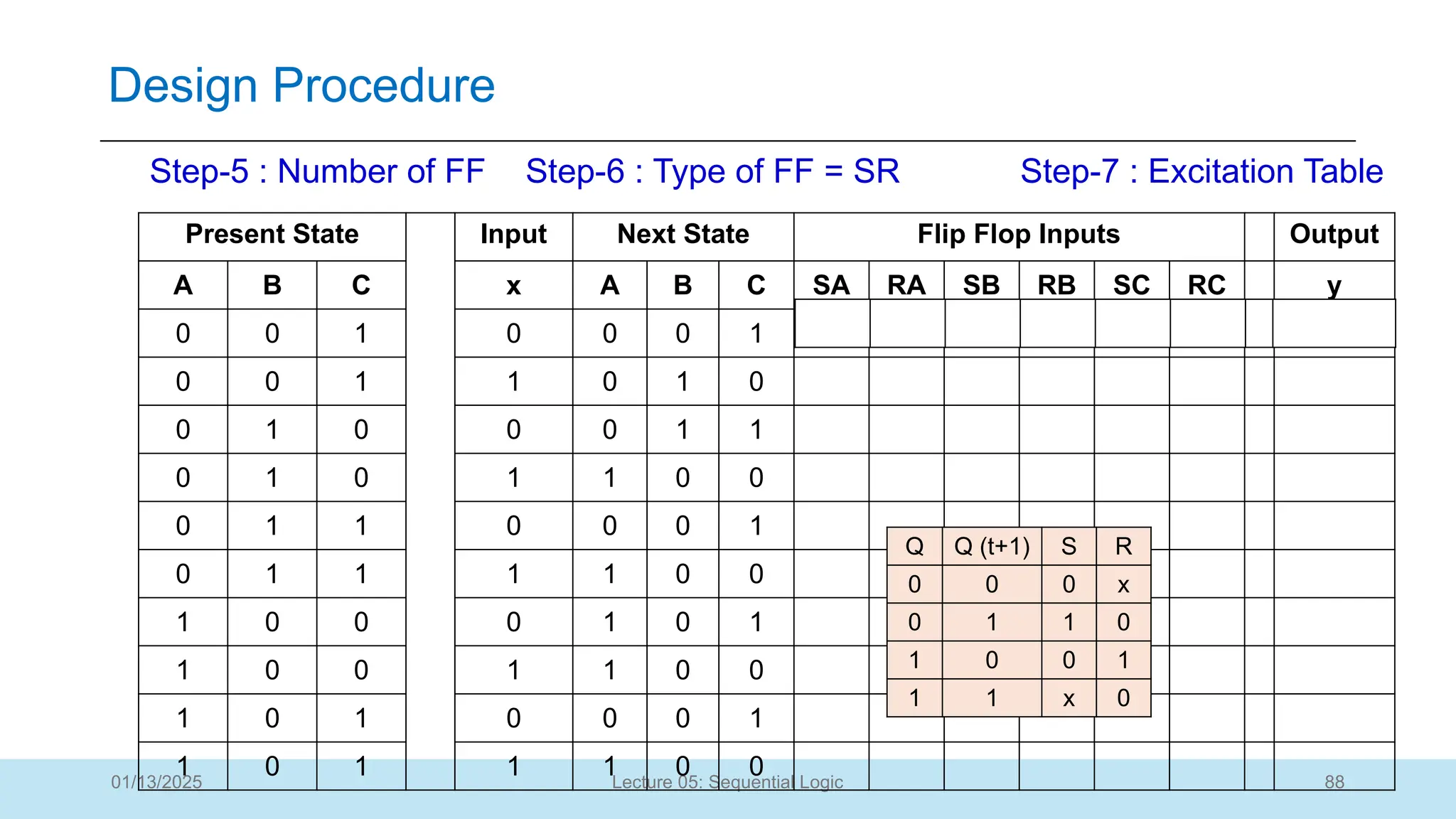
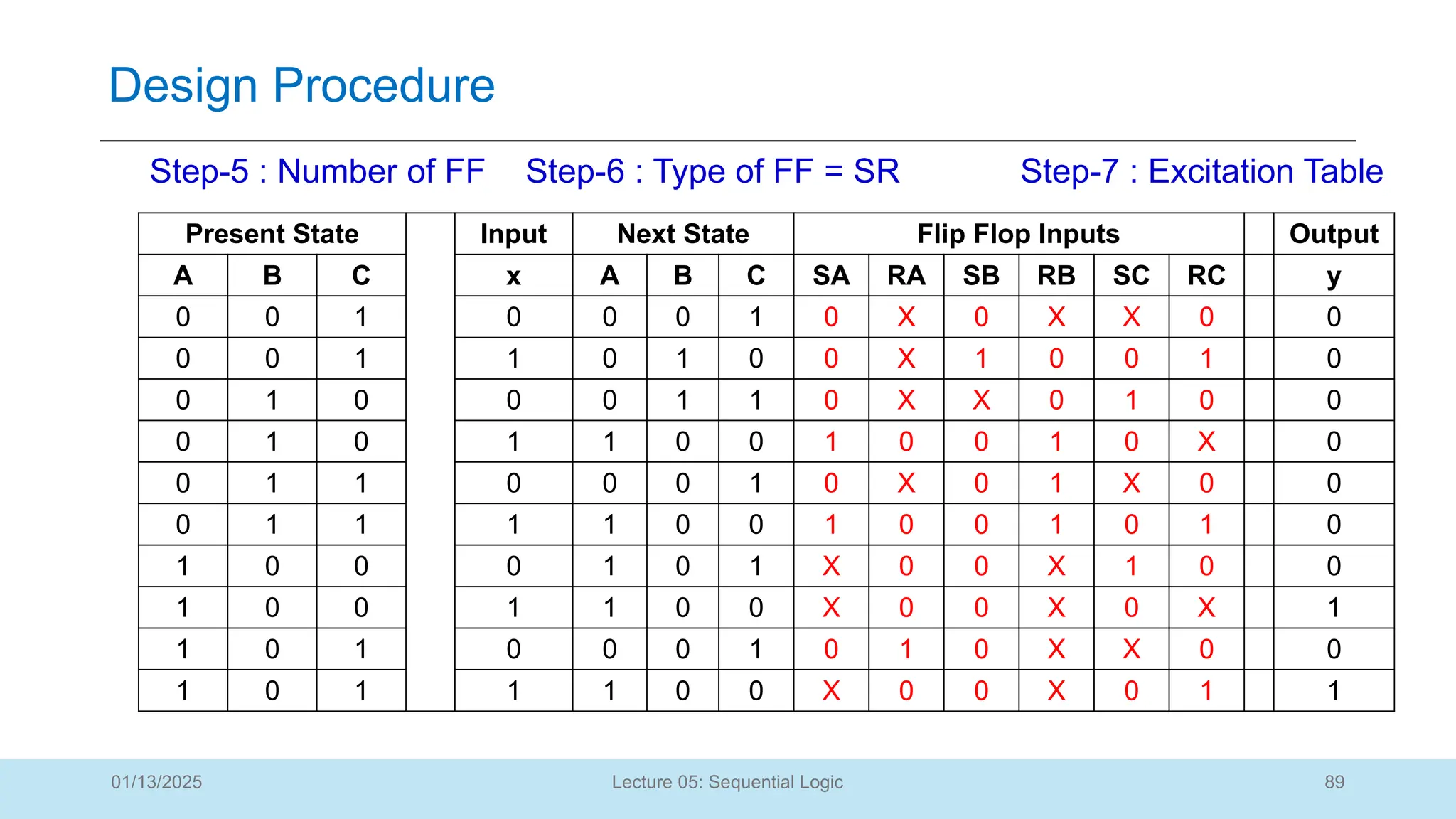
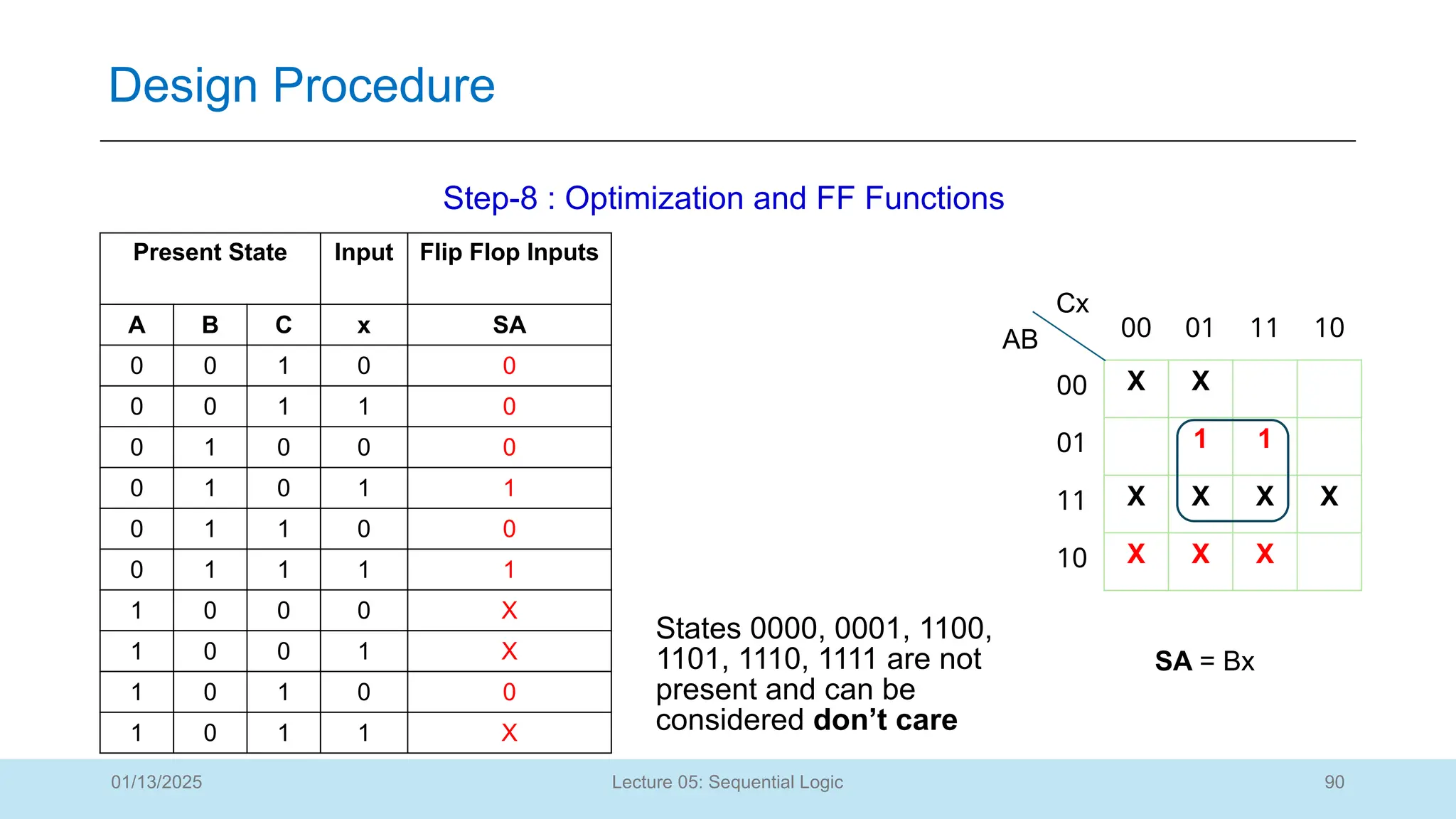
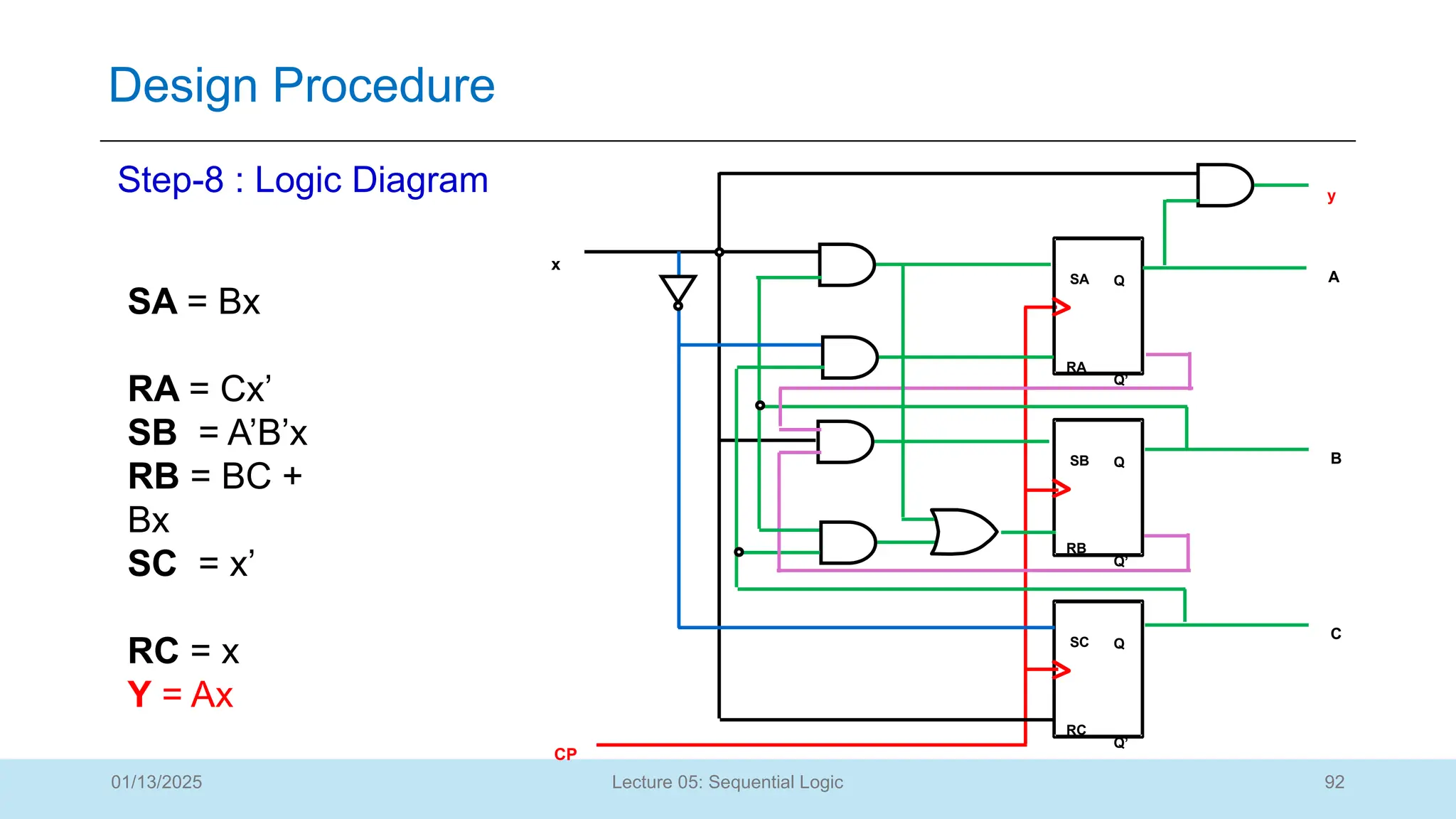
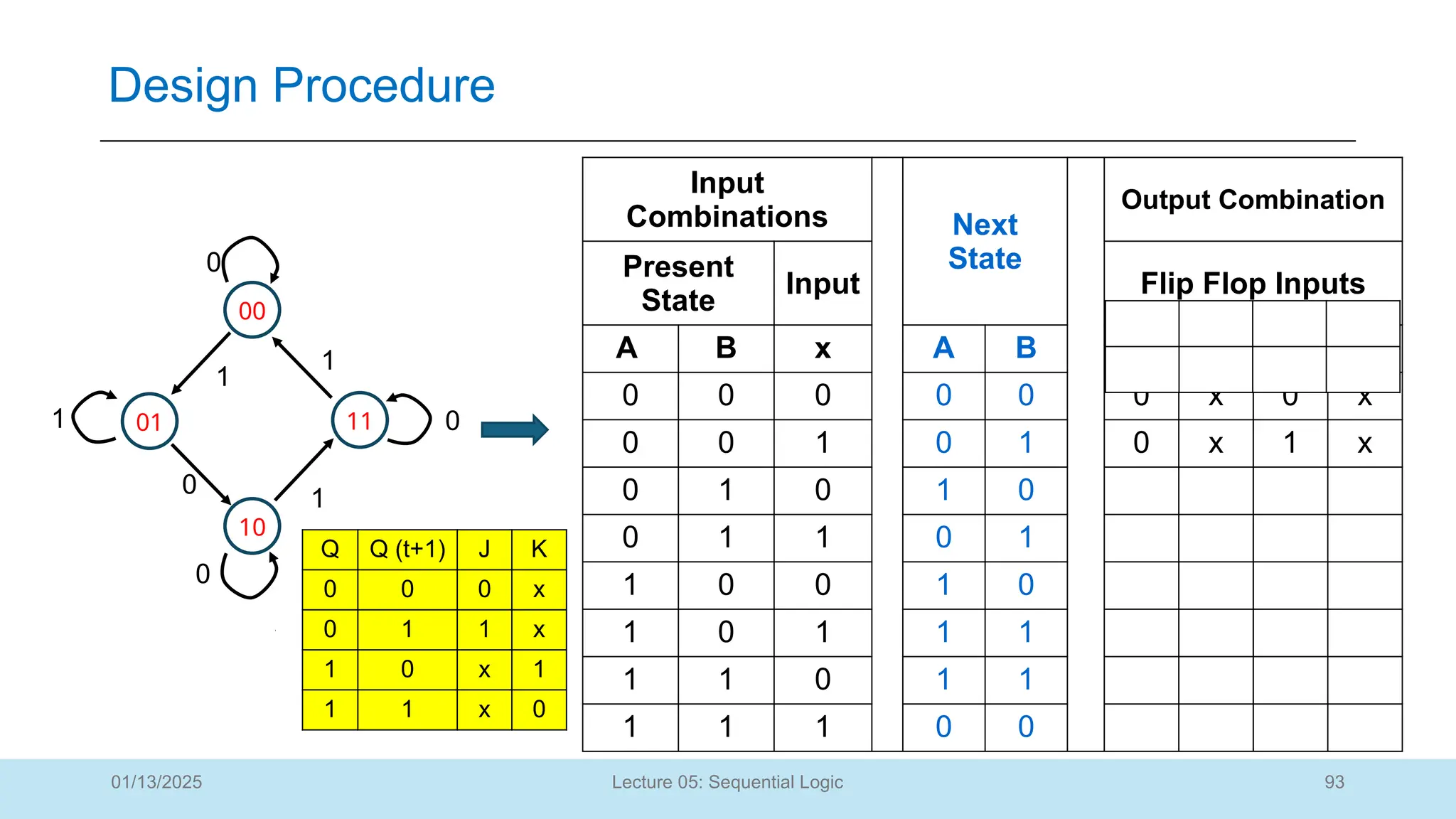
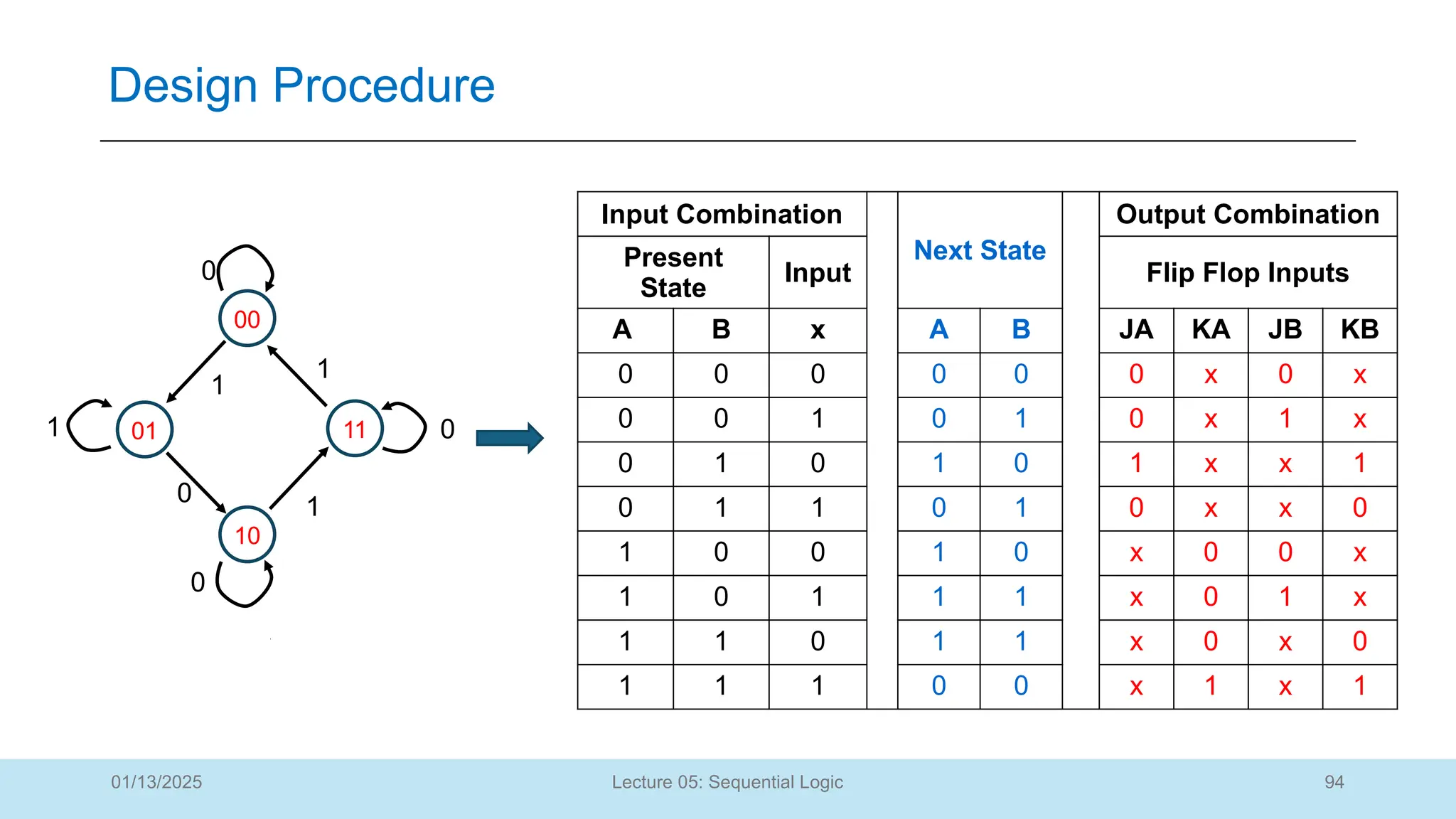
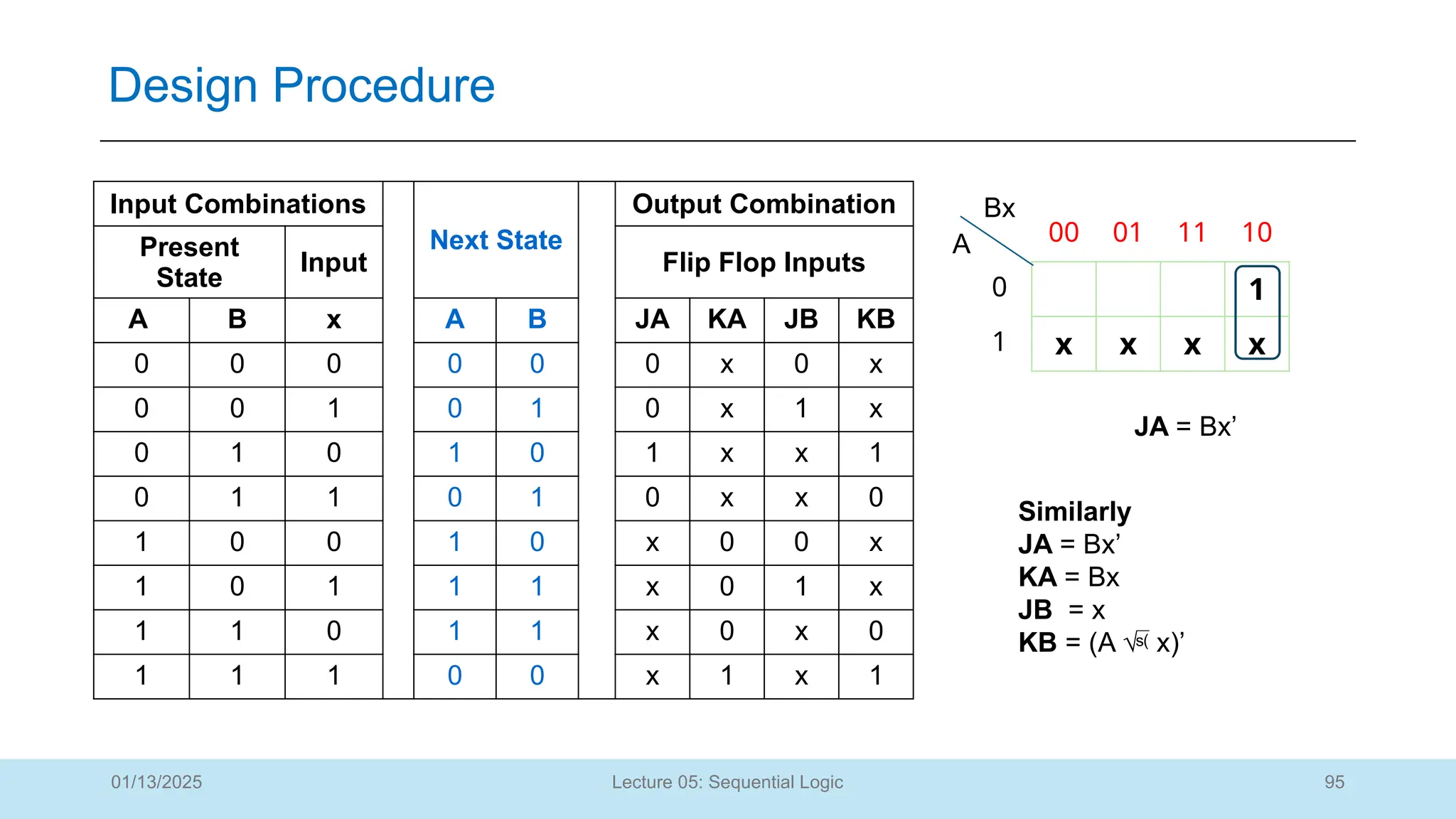
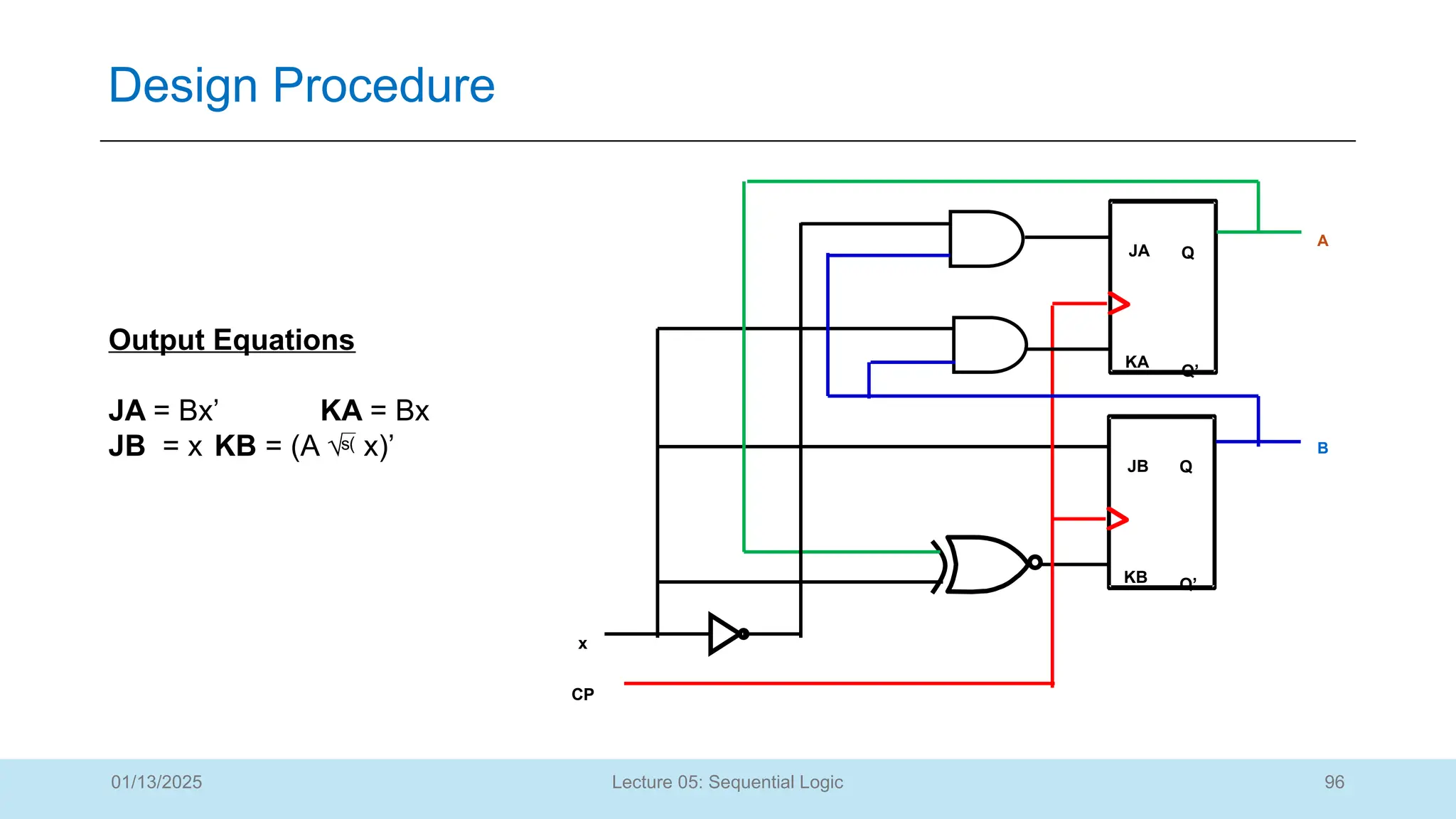
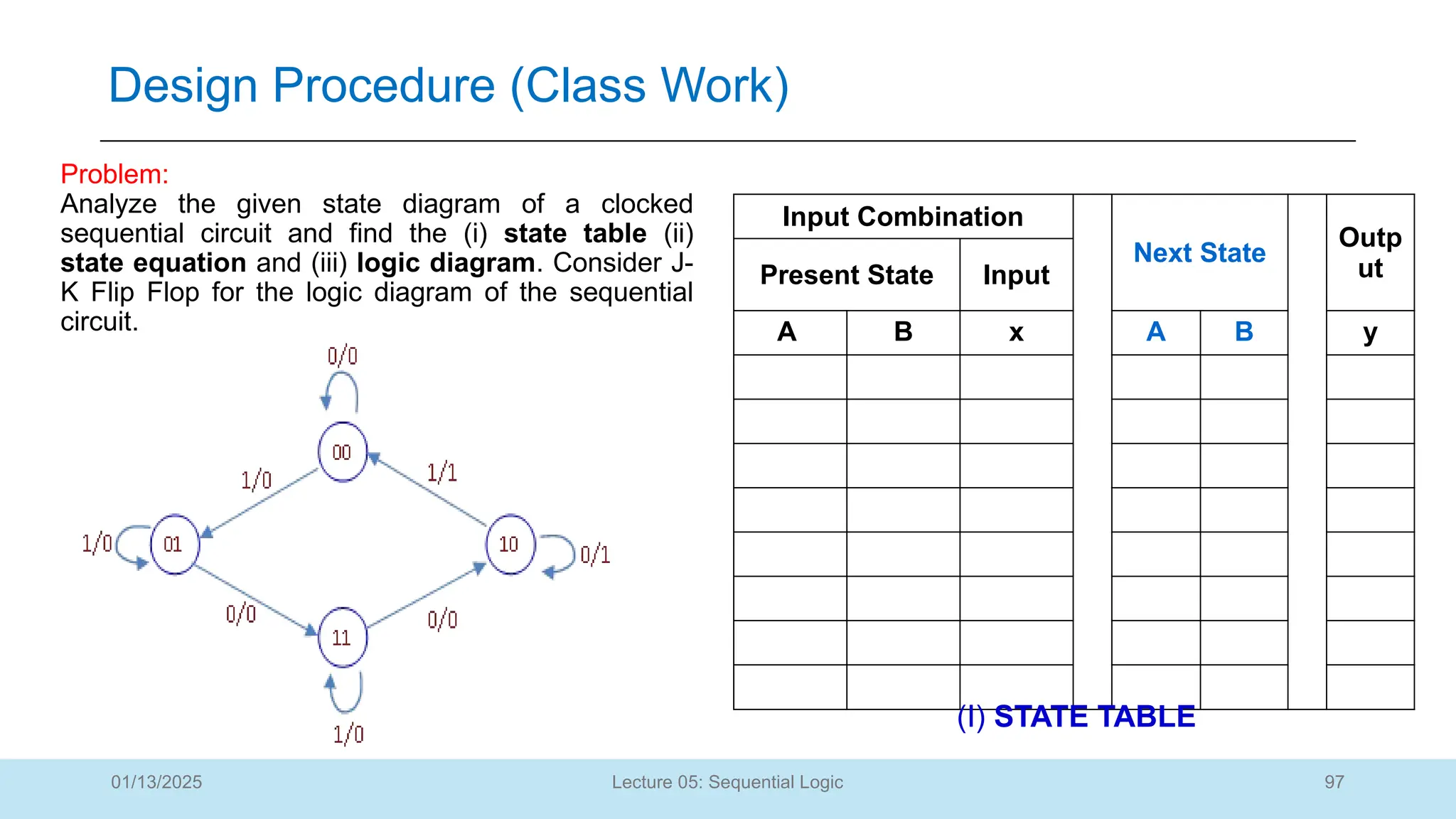
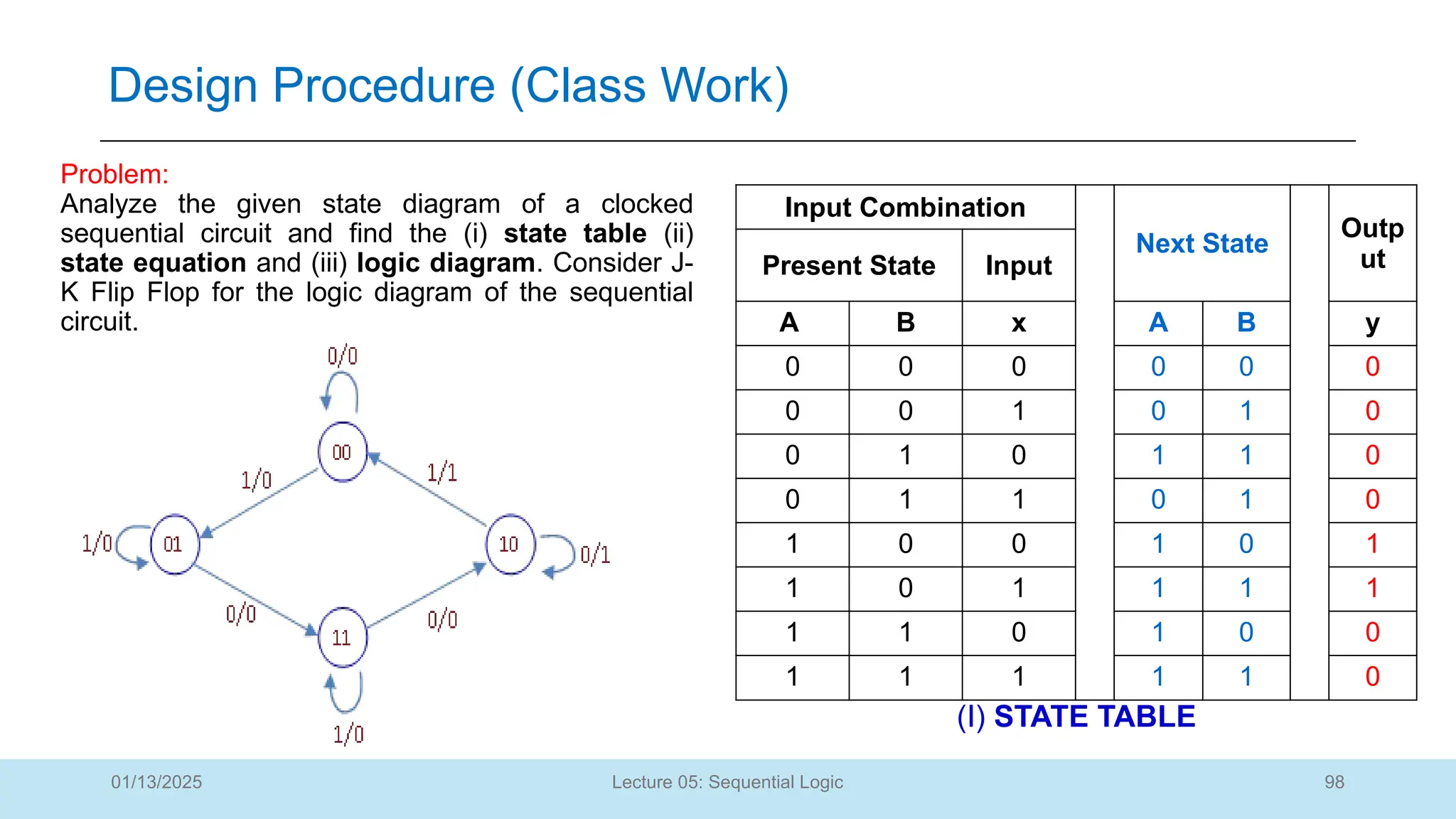
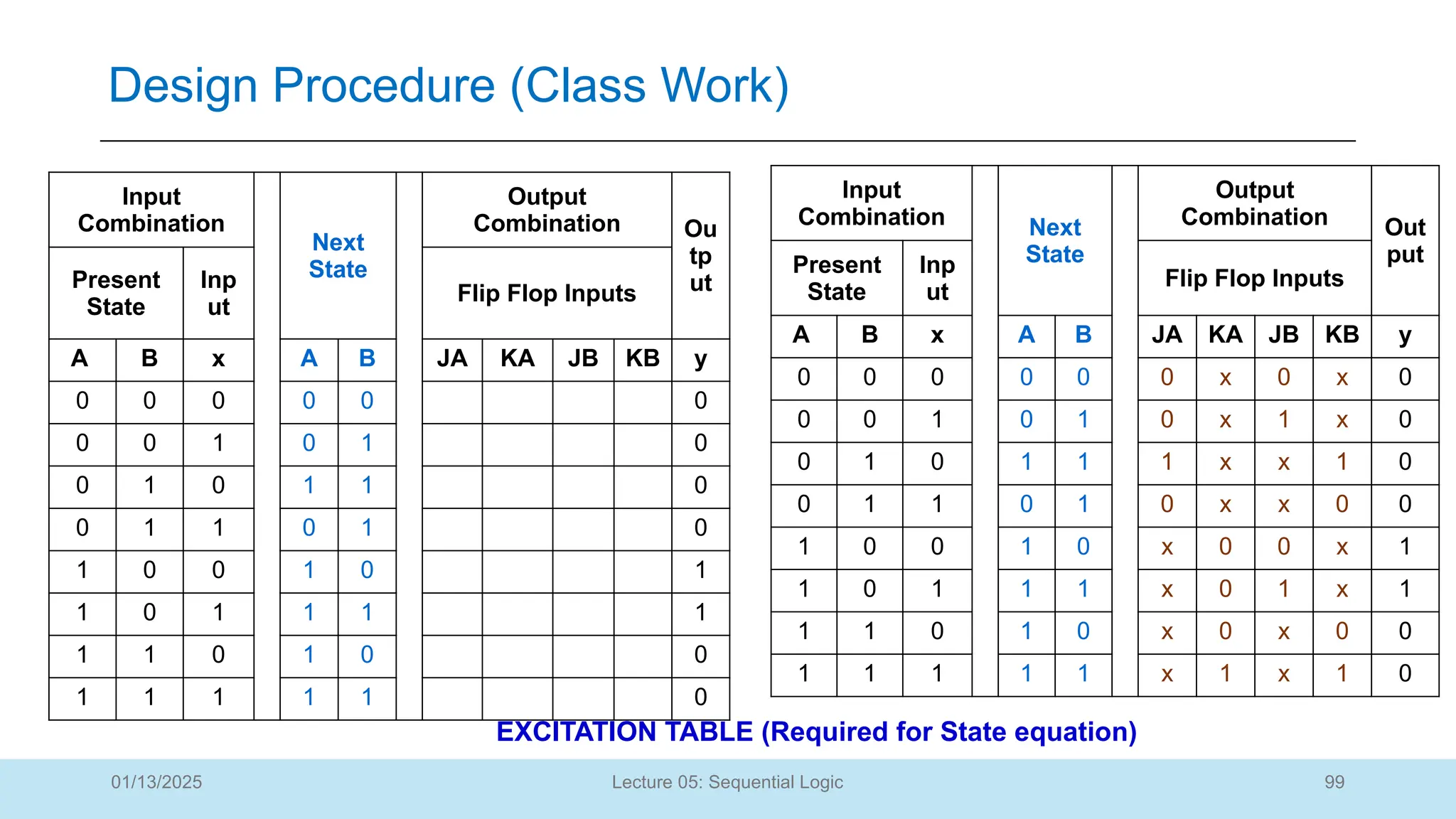
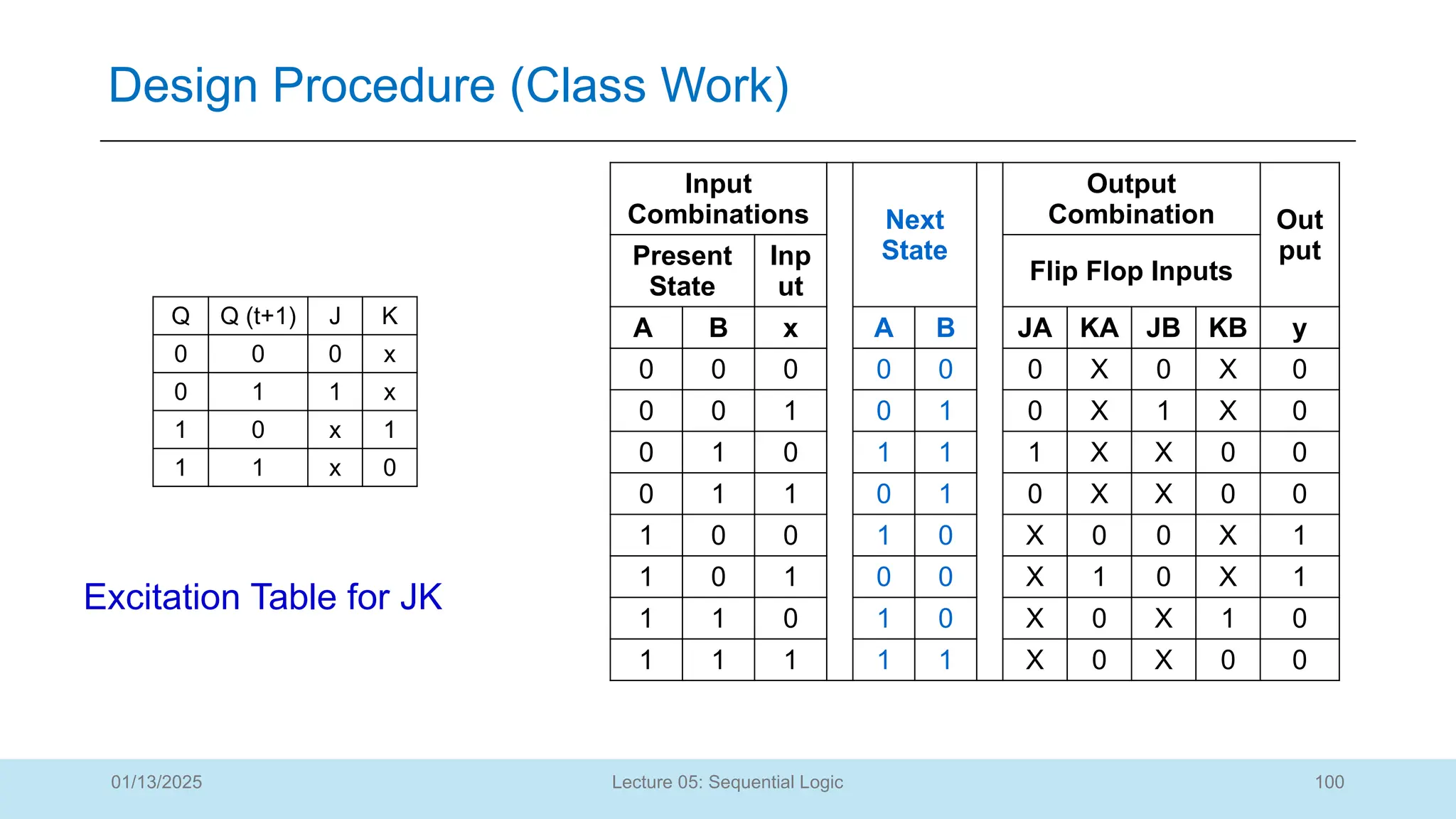
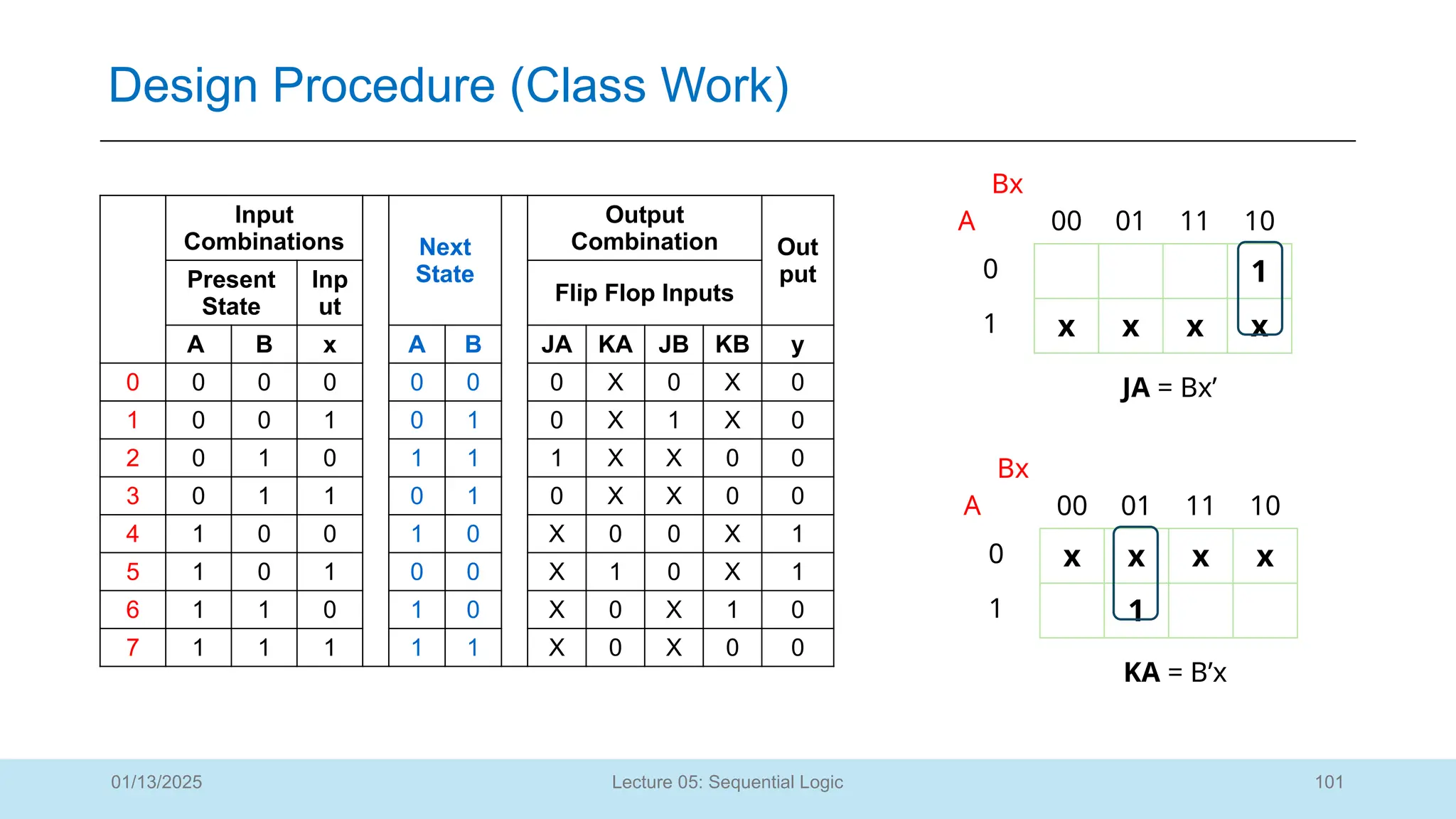
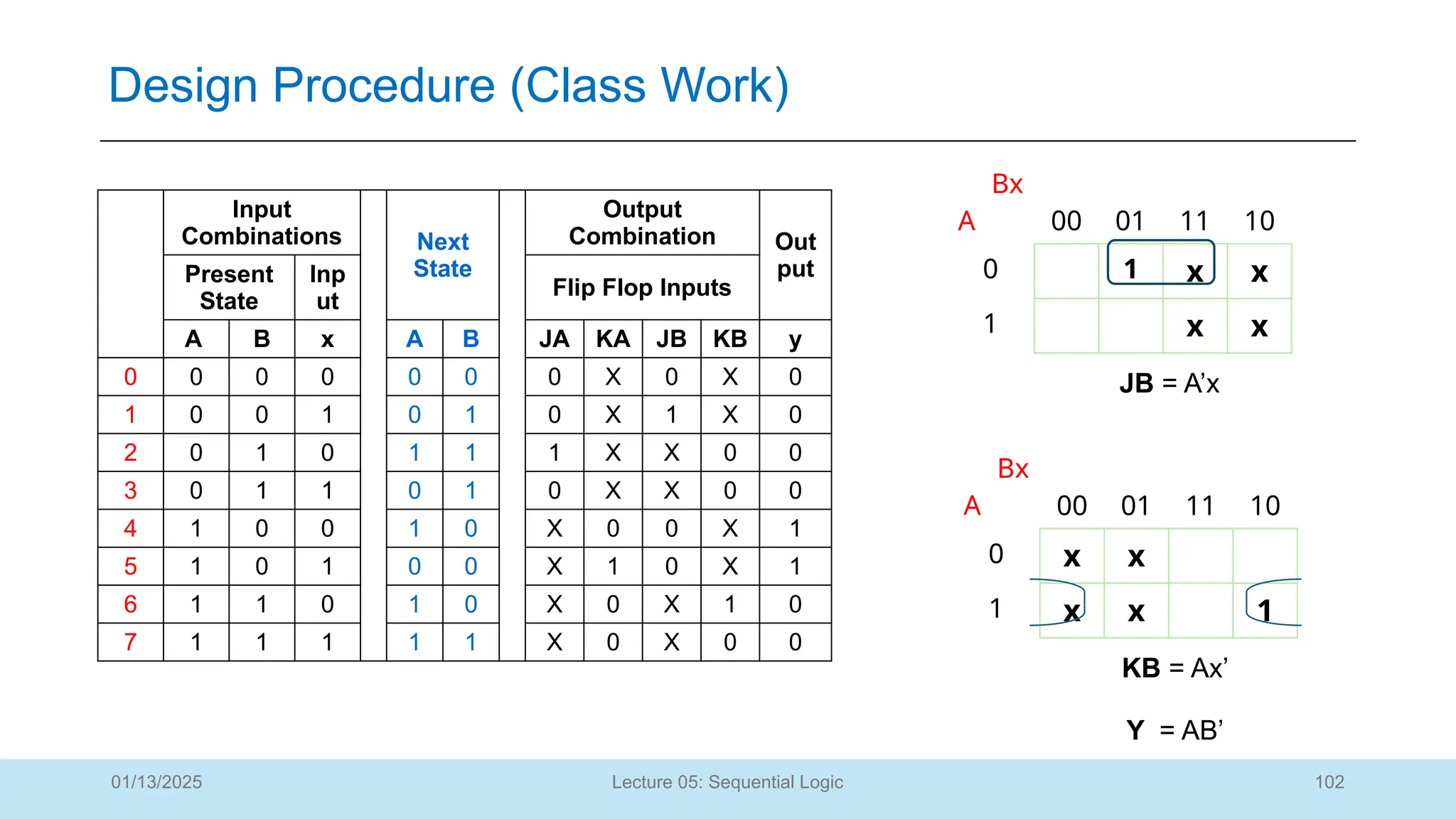
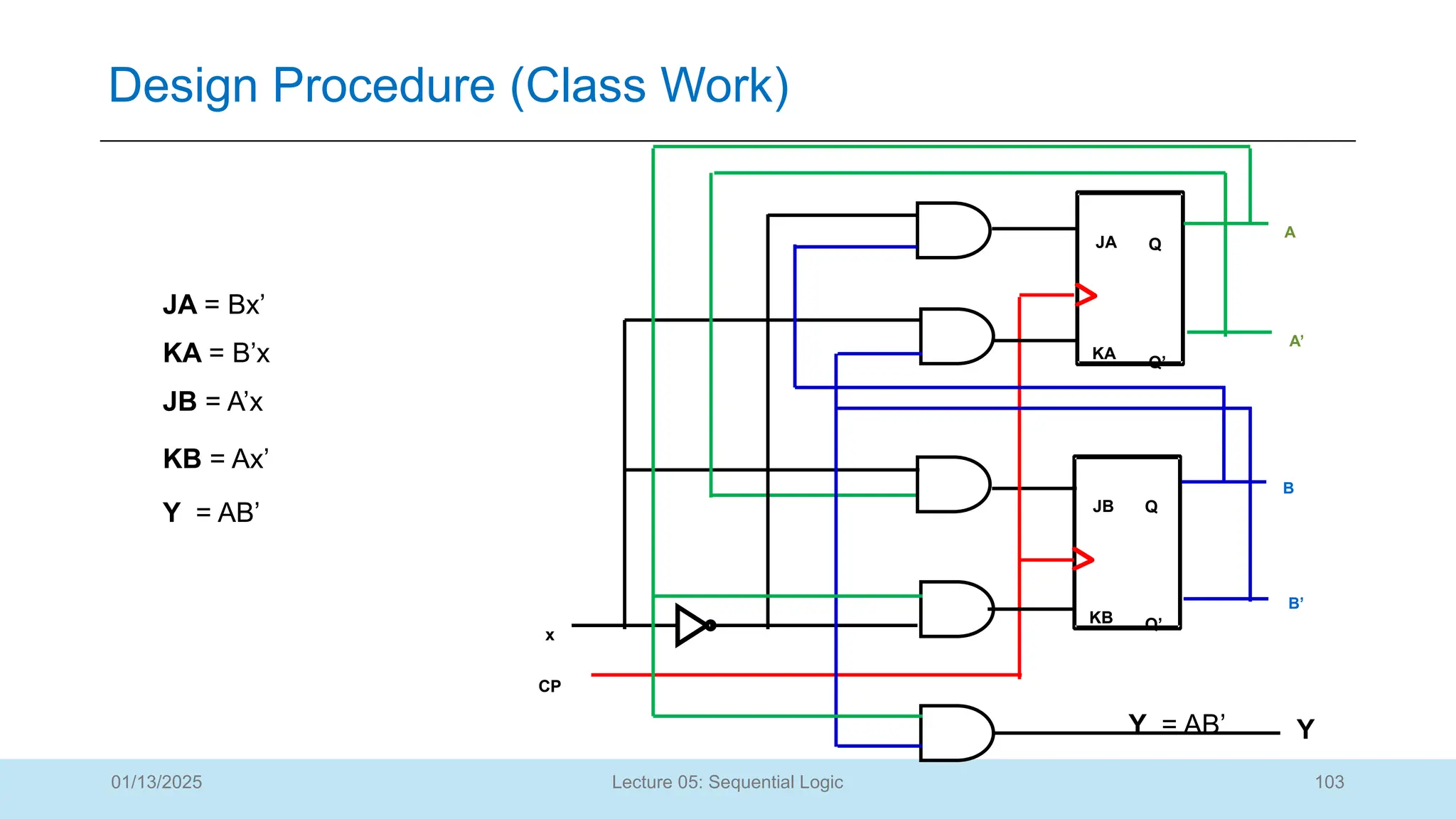
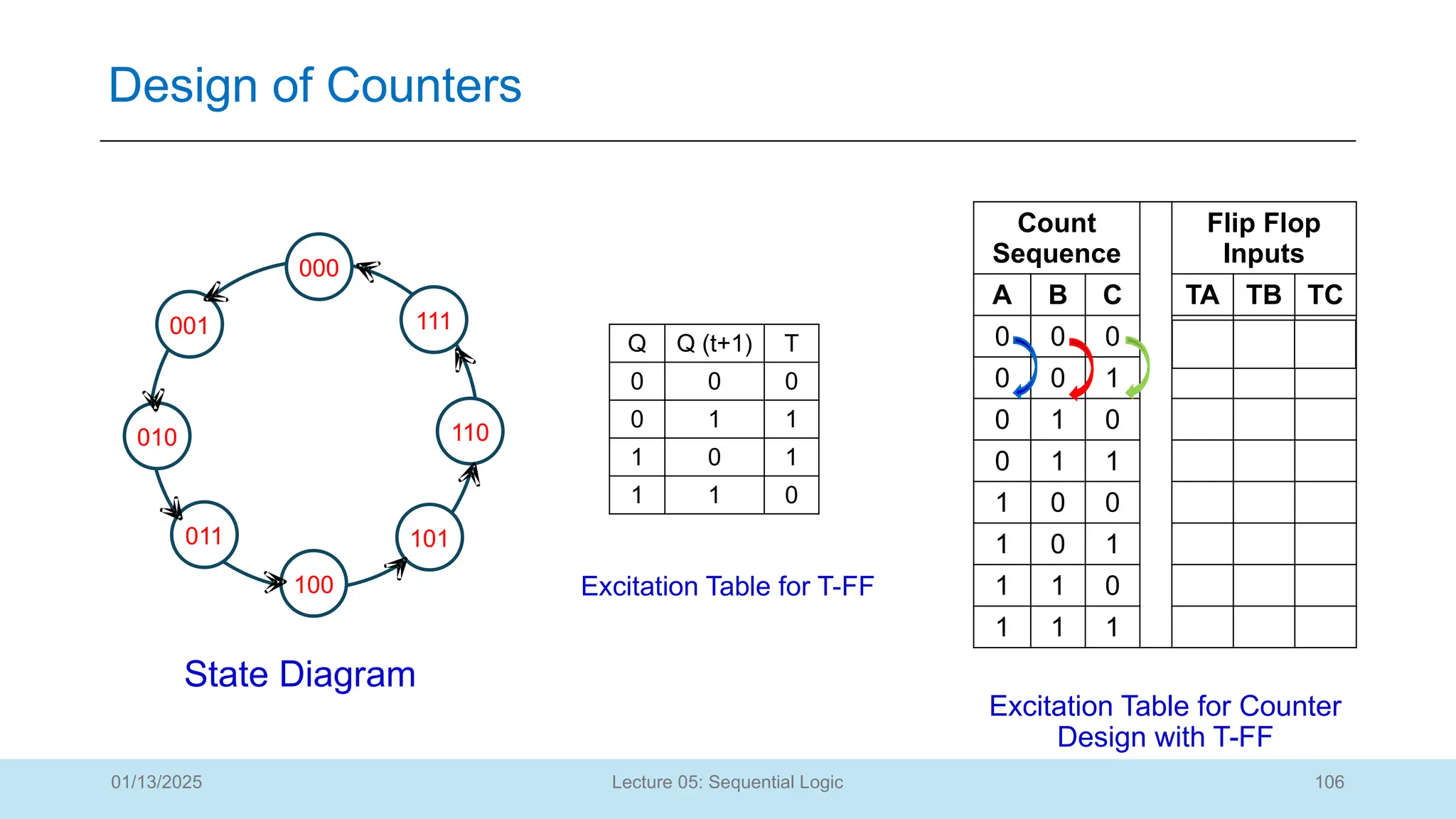
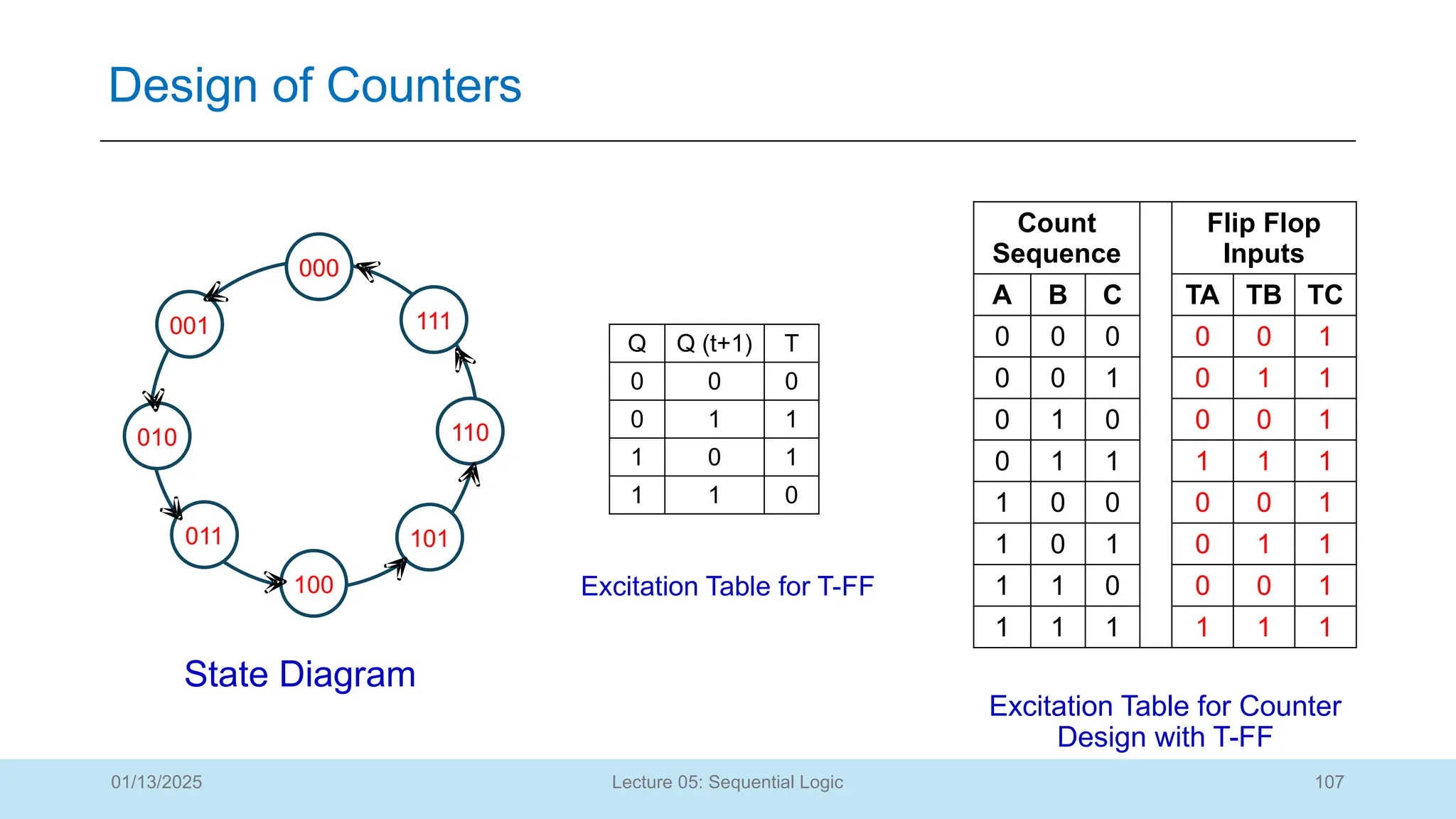
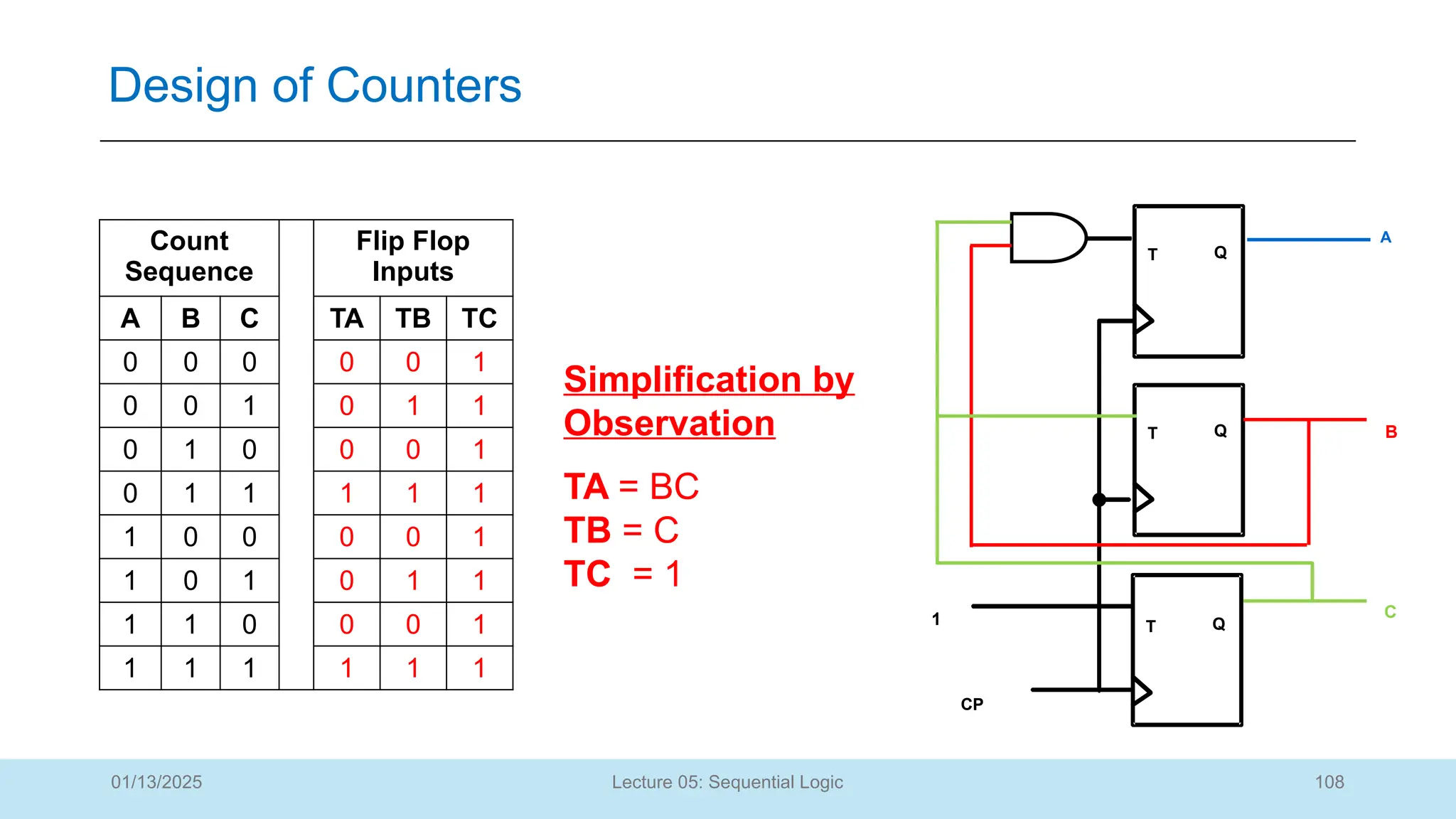
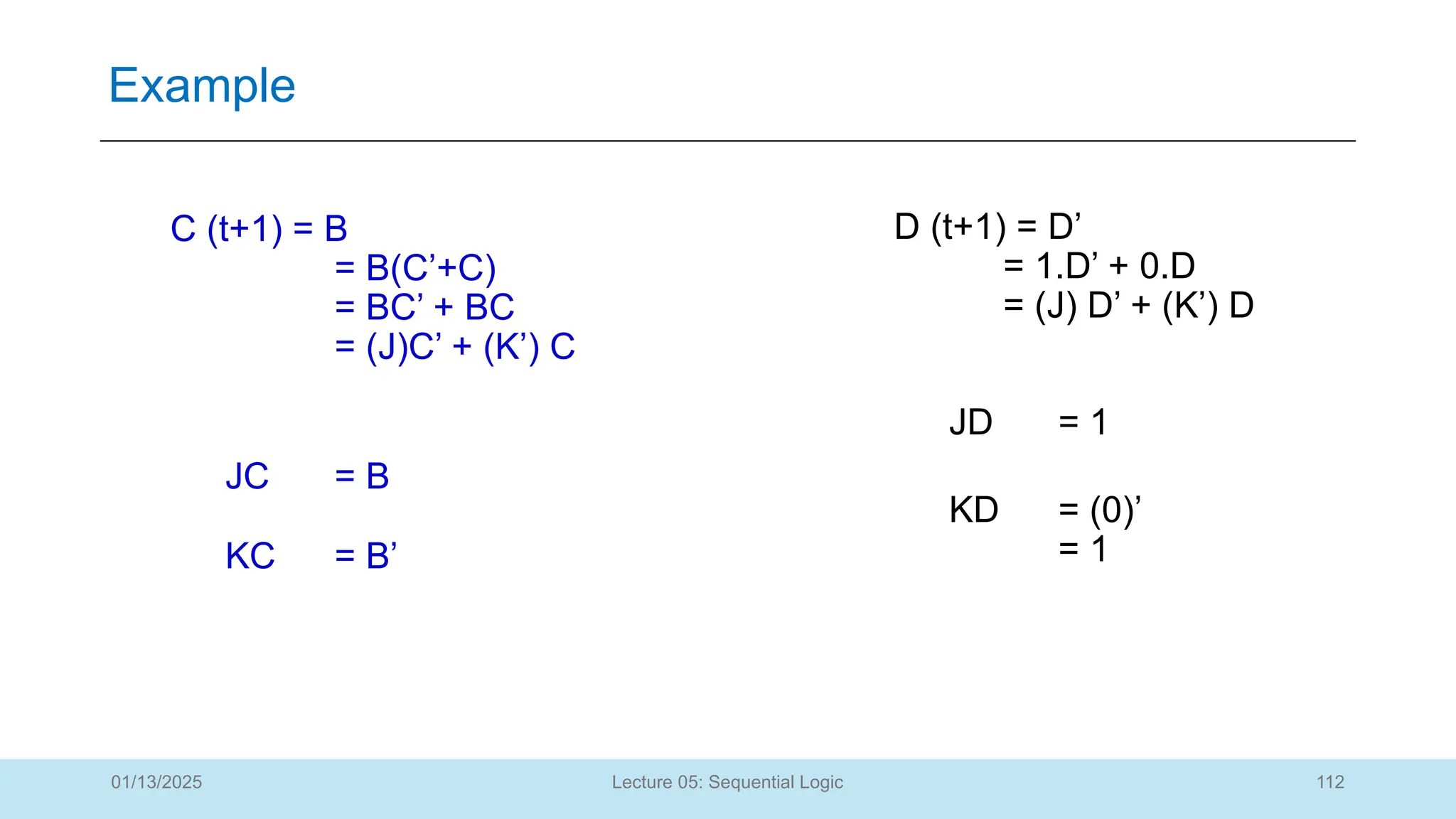
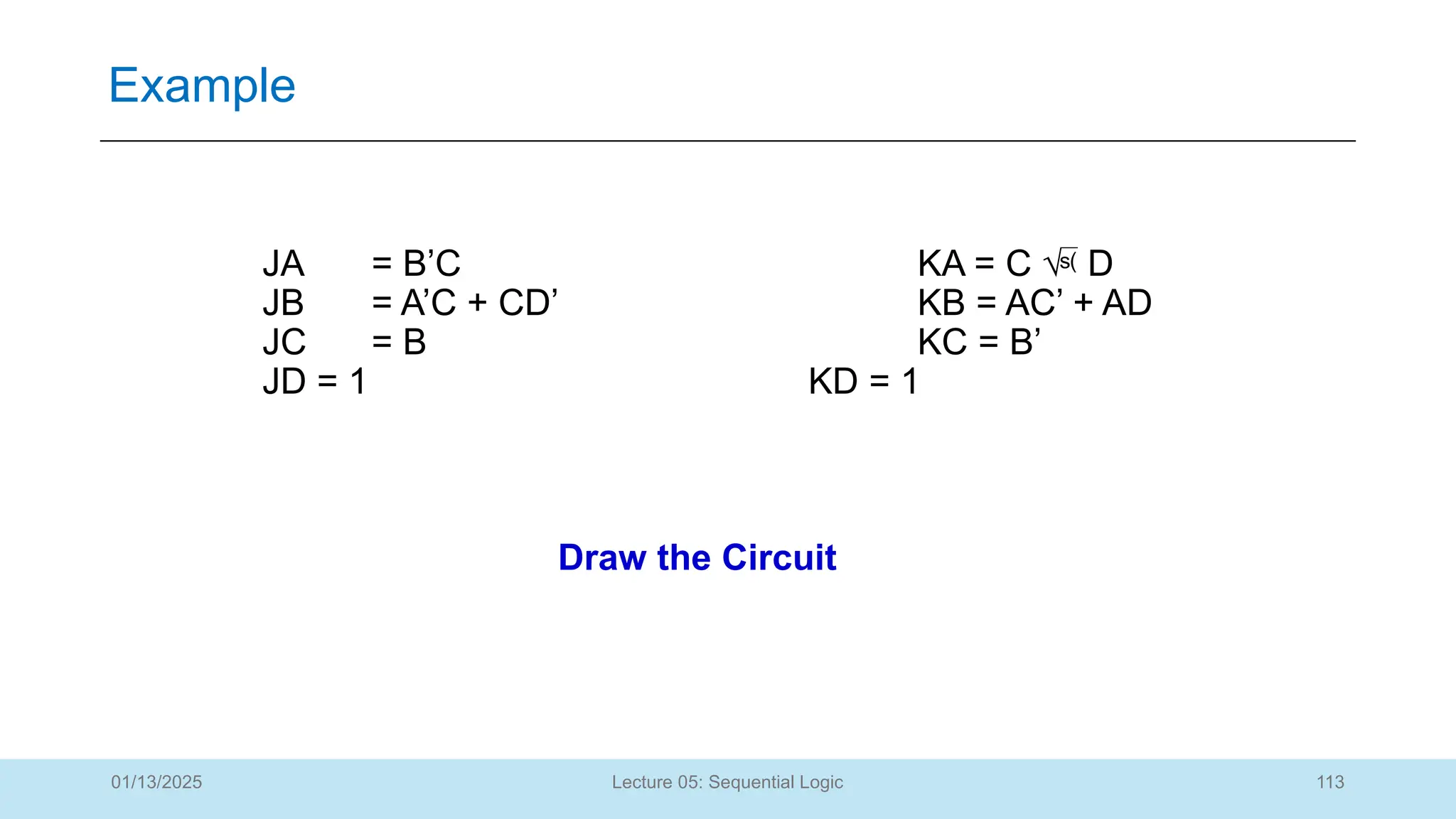
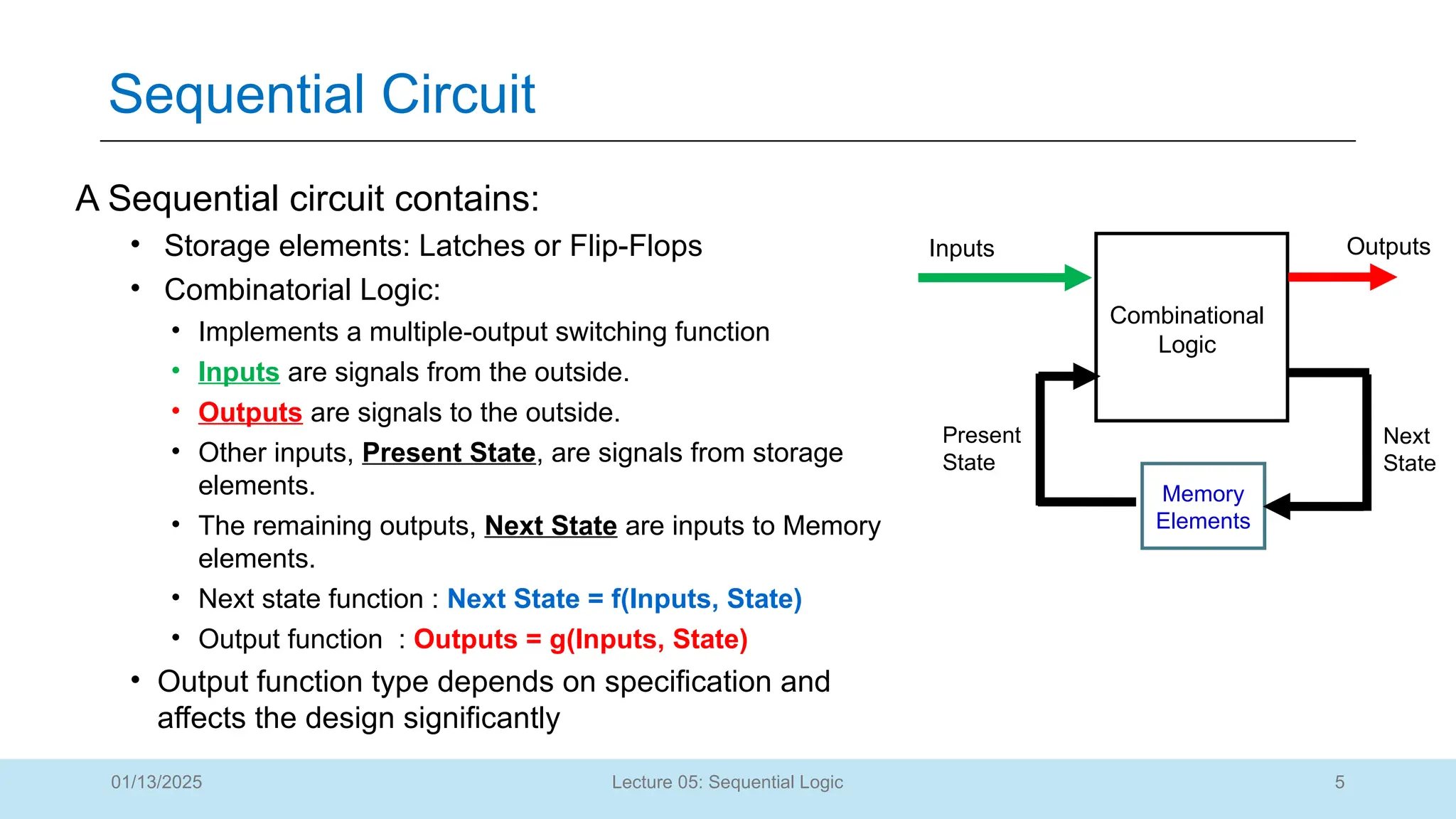
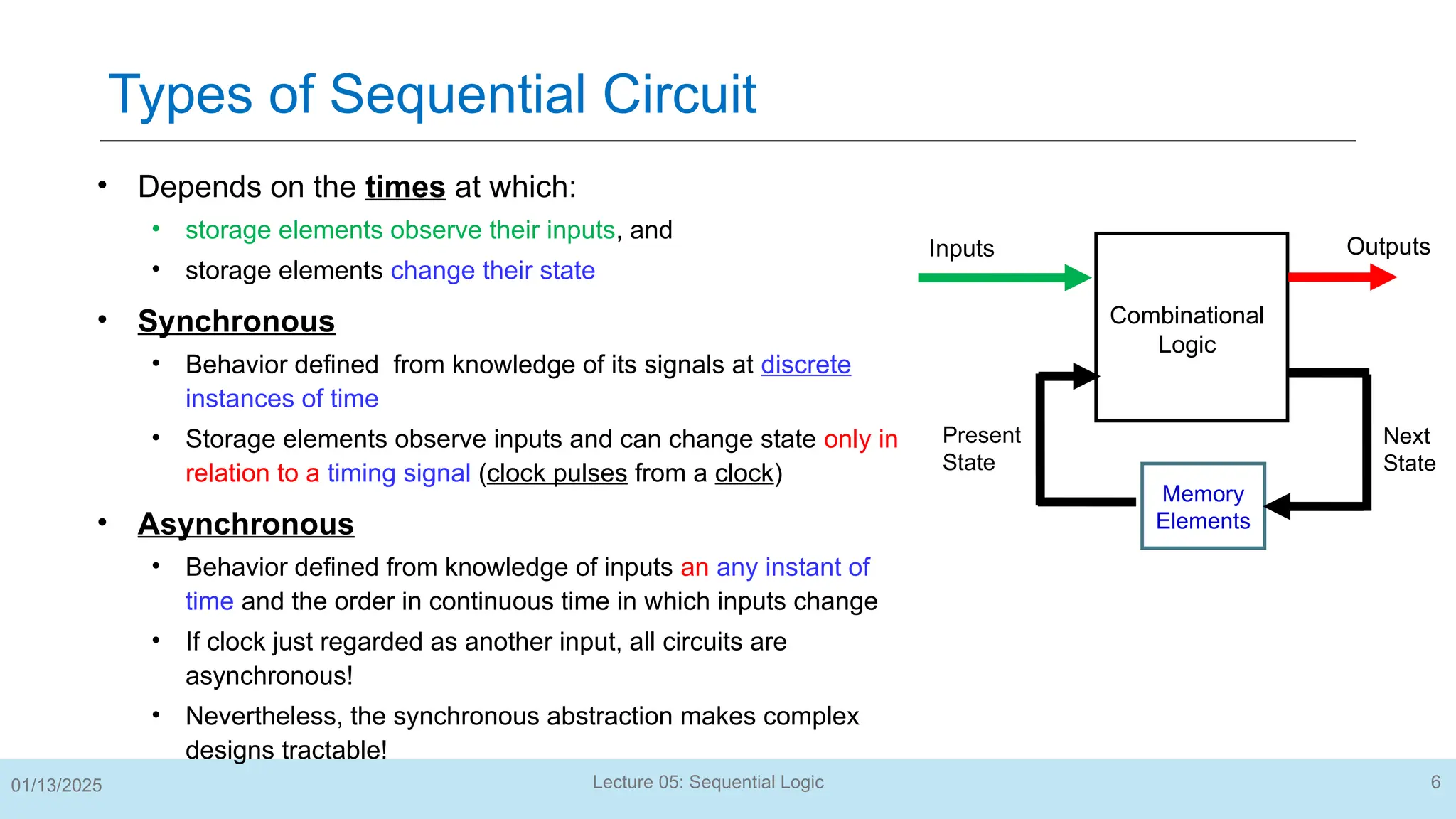
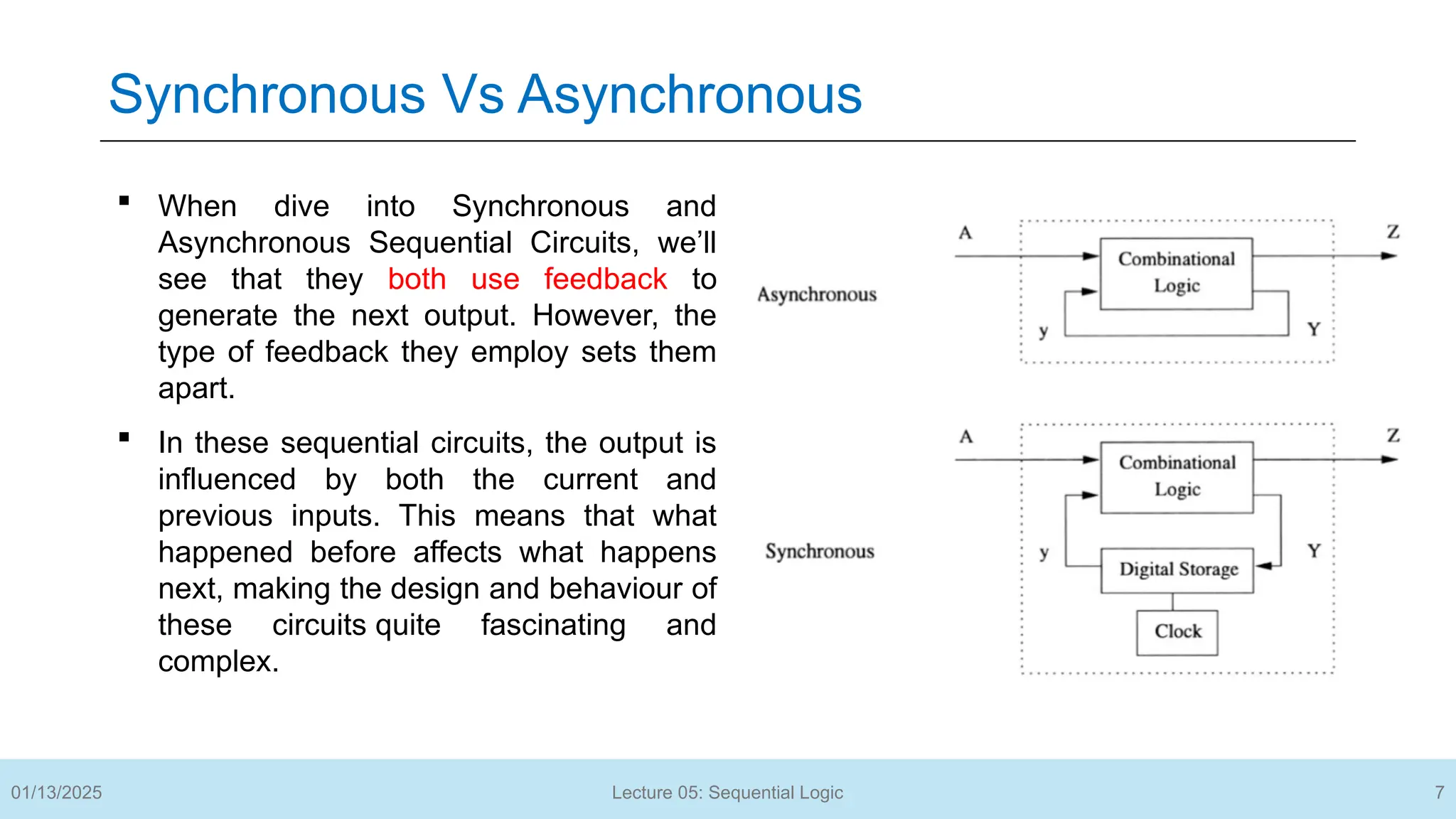
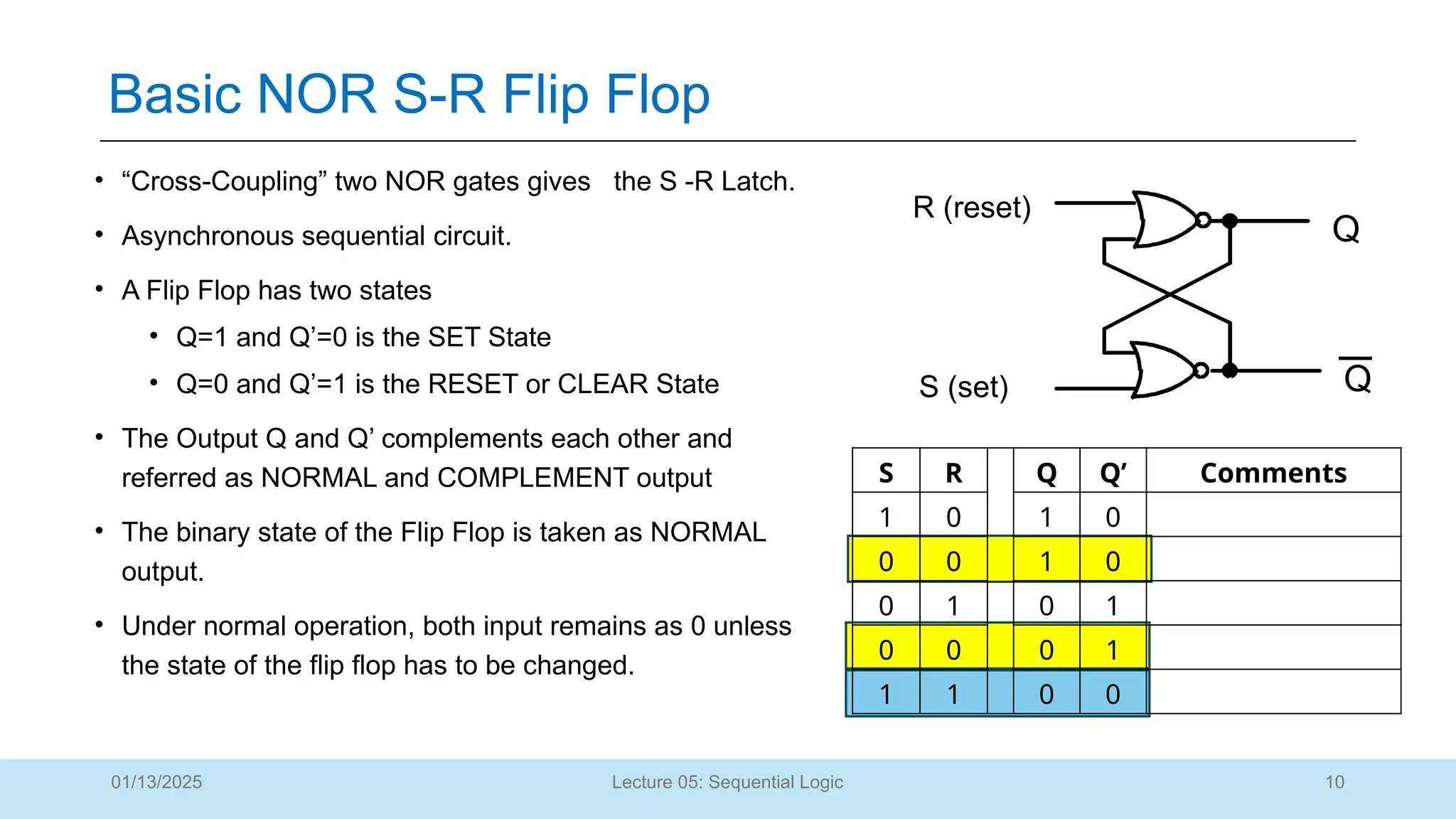
The document outlines a lecture on sequential logic circuits, focusing on components such as latches and flip-flops, and distinguishes between synchronous and asynchronous circuits. It covers various flip-flop types including S-R, D, JK, and T flip-flops, detailing their operations and truth tables. The lecture aims to equip students with the ability to analyze, design, and implement sequential circuits with practical applications in digital systems.

1. 01/13/2025 Lecture 05: Sequential Logic 1
Course Teacher :
Colonel S M Saiful Islam, SUP, psc
CSE (BUET), MBA (IBA), MDS
ITIL®
(Expert), Prince2®
(Practitioner), CDCP®
, ISO 27001 Lead Auditor®
Course Title :
CSE-1201: Digital Logic Design
Credit Hour: 3.0
Department of Computer Science & Engineering
Bangladesh University of Professionals
Lecture 05
SEQUENTIAL LOGIC

2. 2
Lecture 05: Sequential Logic
Learning Objective
 Explain the fundamental components of sequential circuits, including latches,
flip-flops, and their interaction with combinational logic.
 Compare the behaviors of synchronous and asynchronous sequential circuits
and identify scenarios for their practical application.
 Describe the operation of S-R, JK, D, and T Flip-Flops, including clocked and
edge-triggered variations, and construct truth tables and excitation tables.
 Develop state tables and diagrams for sequential circuits, analyze their
transitions, and perform state reduction and assignment.
 .Construct and analyze counters and other sequential circuits, understanding
their role in digital systems and applications.
01/13/2025

3. 3
Lecture 05: Sequential Logic
Overview
1. Sequential Circuit.
2. Different Types of Flip Flops.
3. Analysis of Clocked Sequential Circuit.
4. State Reduction and Assignment.
5. Design Procedure.
01/13/2025

4. 01/13/2025 Lecture 05: Sequential Logic 4
Topic- 11: Sequential Circuit
(Introduction and Basic Design)​

5. 5
Lecture 05: Sequential Logic
Sequential Circuit
01/13/2025
A Sequential circuit contains:
• Storage elements: Latches or Flip-Flops
• Combinatorial Logic:
• Implements a multiple-output switching function
• Inputs are signals from the outside.
• Outputs are signals to the outside.
• Other inputs, Present State, are signals from storage
elements.
• The remaining outputs, Next State are inputs to Memory
elements.
• Next state function : Next State = f(Inputs, State)
• Output function : Outputs = g(Inputs, State)
• Output function type depends on specification and
affects the design significantly
Combinational
Logic
Memory
Elements
Inputs Outputs
Present
State
Next
State

6. 6
Lecture 05: Sequential Logic
Types of Sequential Circuit
01/13/2025
Combinational
Logic
Memory
Elements
Inputs Outputs
Present
State
Next
State
• Depends on the times at which:
• storage elements observe their inputs, and
• storage elements change their state
• Synchronous
• Behavior defined from knowledge of its signals at discrete
instances of time
• Storage elements observe inputs and can change state only in
relation to a timing signal (clock pulses from a clock)
• Asynchronous
• Behavior defined from knowledge of inputs an any instant of
time and the order in continuous time in which inputs change
• If clock just regarded as another input, all circuits are
asynchronous!
• Nevertheless, the synchronous abstraction makes complex
designs tractable!

7. 7
Lecture 05: Sequential Logic
Synchronous Vs Asynchronous
01/13/2025
 When dive into Synchronous and
Asynchronous Sequential Circuits, we’ll
see that they both use feedback to
generate the next output. However, the
type of feedback they employ sets them
apart.
 In these sequential circuits, the output is
influenced by both the current and
previous inputs. This means that what
happened before affects what happens
next, making the design and behaviour of
these circuits quite fascinating and
complex.

8. 8
Lecture 05: Sequential Logic
Synchronous Vs Asynchronous
01/13/2025
Key Synchronous Sequential Circuits Asynchronous Sequential Circuits
Definition
Asynchronous sequential circuits are digital
sequential circuits in which the feedback to the
input for next output generation is governed by
clock signals.
Asynchronous sequential circuits are digital
sequential circuits in which the feedback to the
input for next output generation is not governed
by clock signals.
Memory Unit
In Synchronous sequential circuits, the memory
unit which is being get used for governance is
clocked flip flop.
Unclocked flip flop or time delay is used as
memory element in case of Asynchronous
sequential circuits.
State
The states of Synchronous sequential circuits
are always predictable and thus reliable.
There are chances for the Asynchronous circuits
to enter into a wrong state because of the time
difference between the arrivals of inputs. This is
called "race condition".
Complexity
It is easy to design Synchronous sequential
circuits
The presence of feedback among logic gates
causes instability issues making the design of
Asynchronous sequential circuits difficult.

9. 01/13/2025 Lecture 05: Sequential Logic 9
Topic- 12: Different Types of Flip Flop (S-R, RS,
D, JK, T )​

10. 10
Lecture 05: Sequential Logic
Basic NOR S-R Flip Flop
01/13/2025
• “Cross-Coupling” two NOR gates gives the S -R Latch.
• Asynchronous sequential circuit.
• A Flip Flop has two states
• Q=1 and Q’=0 is the SET State
• Q=0 and Q’=1 is the RESET or CLEAR State
• The Output Q and Q’ complements each other and
referred as NORMAL and COMPLEMENT output
• The binary state of the Flip Flop is taken as NORMAL
output.
• Under normal operation, both input remains as 0 unless
the state of the flip flop has to be changed.
S R Q Q’ Comments
1 0 1 0
0 0 1 0
0 1 0 1
0 0 0 1
1 1 0 0
S (set)
R (reset)
Q
Q

11. 11
Lecture 05: Sequential Logic
Basic NOR S-R Flip Flop
01/13/2025
• “Cross-Coupling” two NOR gates gives the S -R Latch.
• Asynchronous sequential circuit.
• A Flip Flop has two states
• Q=1 and Q’=0 is the SET State
• Q=0 and Q’=1 is the RESET or CLEAR State
• The Output Q and Q’ complements each other and
referred as NORMAL and COMPLEMENT output
• The binary state of the Flip Flop is taken as NORMAL
output.
• Under normal operation, both input remains as 0 unless
the state of the flip flop has to be changed.
• S = 0, R = 0; next state is same as present state
• S = 1, R = 1; is indeterminate as input pattern
S R Q Q’ Comments
1 0 1 0 “Set” Q to 1
0 0 1 0 No Change of
State
0 1 0 1 “Reset” Q to 0
0 0 0 1 No Change of
State
1 1 0 0 Indeterminate
S (set)
R (reset)
Q
Q

12. 12
Lecture 05: Sequential Logic
Basic NAND S-R Flip Flop
01/13/2025
• “Cross-Coupling” two NAND gates gives the S -R
Latch:
• Asynchronous sequential circuit.
• A Flip Flop has two states
• Q=1 and Q’=0 is the SET State
• Q=0 and Q’=1 is the RESET or CLEAR State
• The Output Q and Q’ complements each other and
referred as NORMAL and COMPLEMENT output
• The binary state of the Flip Flop is taken as NORMAL
output.
• Under normal operation, both input remains as 1
unless the state of the flip flop has to be changed.
Q
S (set)
R (reset) Q
S R Q Q’ Comments
1 0 0 1
1 1 0 1
0 1 1 0
1 1 1 0
0 0 1 1

13. 13
Lecture 05: Sequential Logic
Basic NAND S-R Flip Flop
01/13/2025
• “Cross-Coupling” two NAND gates gives the S -R Latch:
• Asynchronous sequential circuit.
• A Flip Flop has two states
• Q=1 and Q’=0 is the SET State
• Q=0 and Q’=1 is the RESET or CLEAR State
• The Output Q and Q’ complements each other and
referred as NORMAL and COMPLEMENT output
• The binary state of the Flip Flop is taken as NORMAL
output.
• Under normal operation, both input remains as 1 unless
the state of the flip flop has to be changed.
• S = 1, R = 1; next state is same as present state
• S = 0, R = 0; is indeterminate as input pattern
Q
S (set)
R (reset) Q
S R Q Q’ Comments
1 0 0 1 “Reset” Q to 0
1 1 0 1 No Change of
State
0 1 1 0 “Set” Q to 1
1 1 1 0 No Change of
State
0 0 1 1 Indeterminate

14. 14
Lecture 05: Sequential Logic
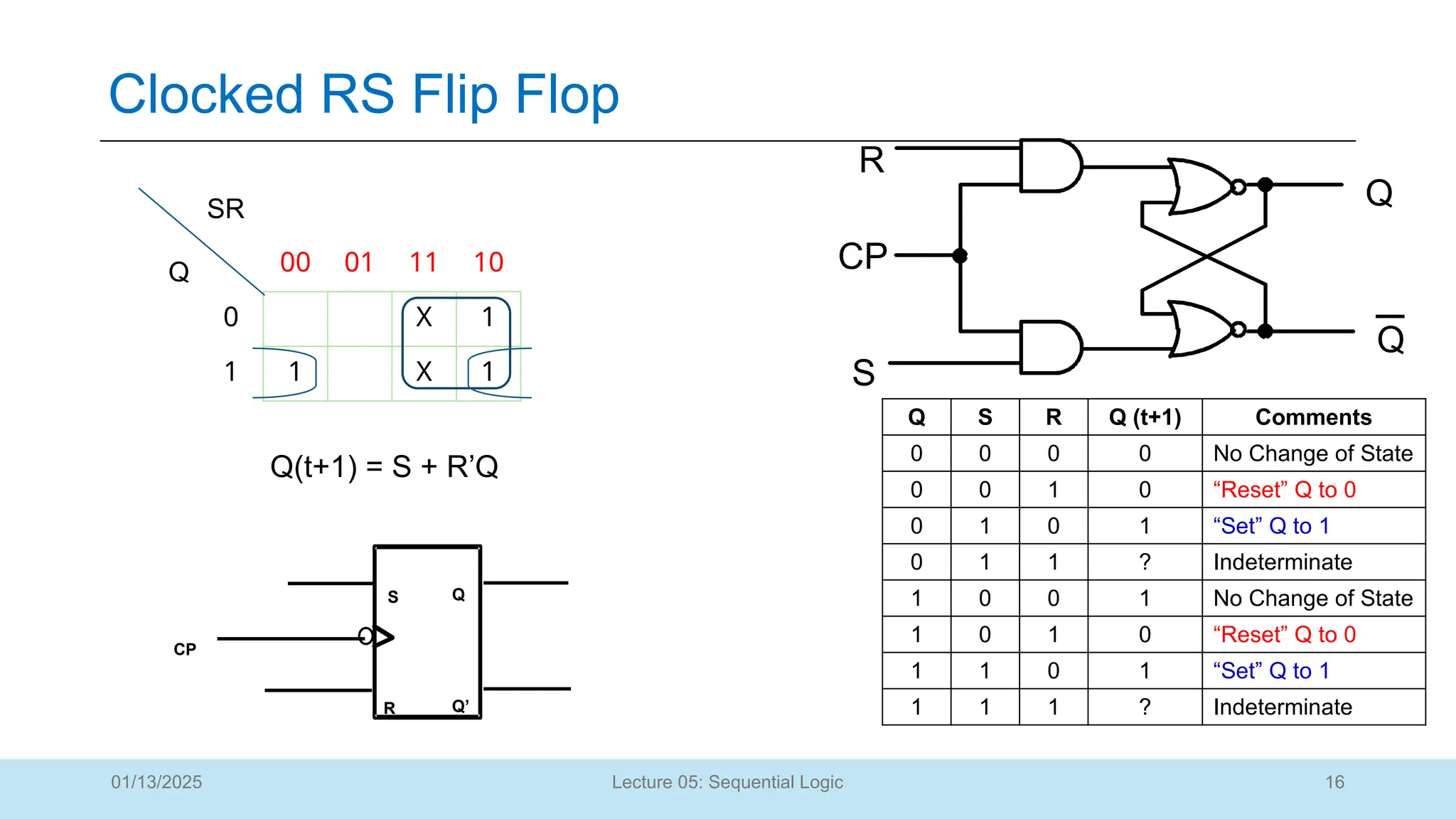
Clocked RS Flip Flop
01/13/2025
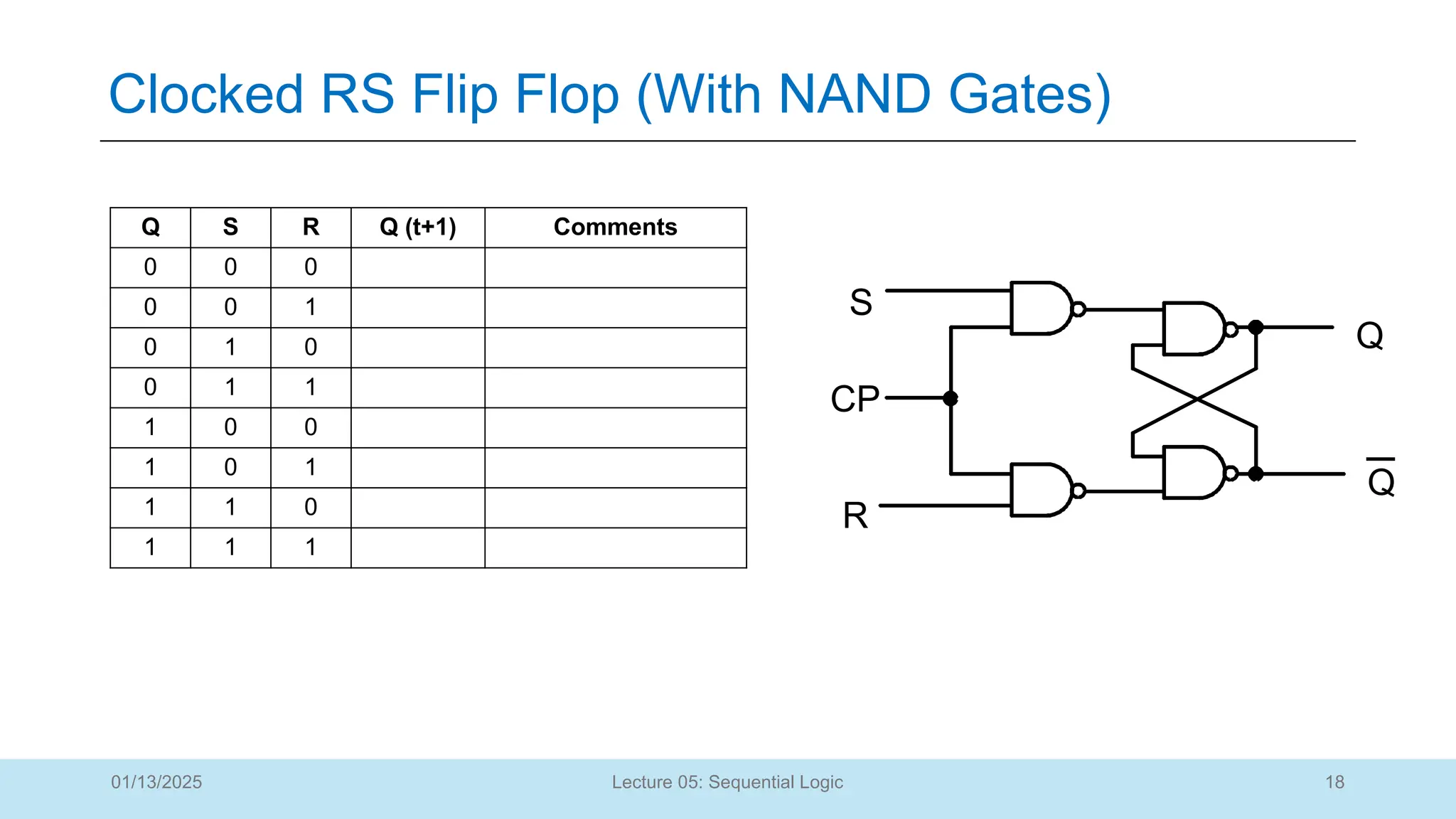
Q S R Q (t+1) Comments
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
• Adding two AND gates to the basic S - R
NOR latch gives the clocked RS Latch:
• Has a time sequence behavior similar to the
basic S-R latch except that the S and R
inputs are only observed when the line C is
high.
• The table describes what happens after the
clock [at time (t+1)] based on:
• Present inputs (S,R) and
• Present State Q(t).
• CP means “Clock Pulse”.
• CP=1, S and R has input and the Flip Flop is in
operation
• CP=0, S=R=0;
R
S
Q
CP
Q

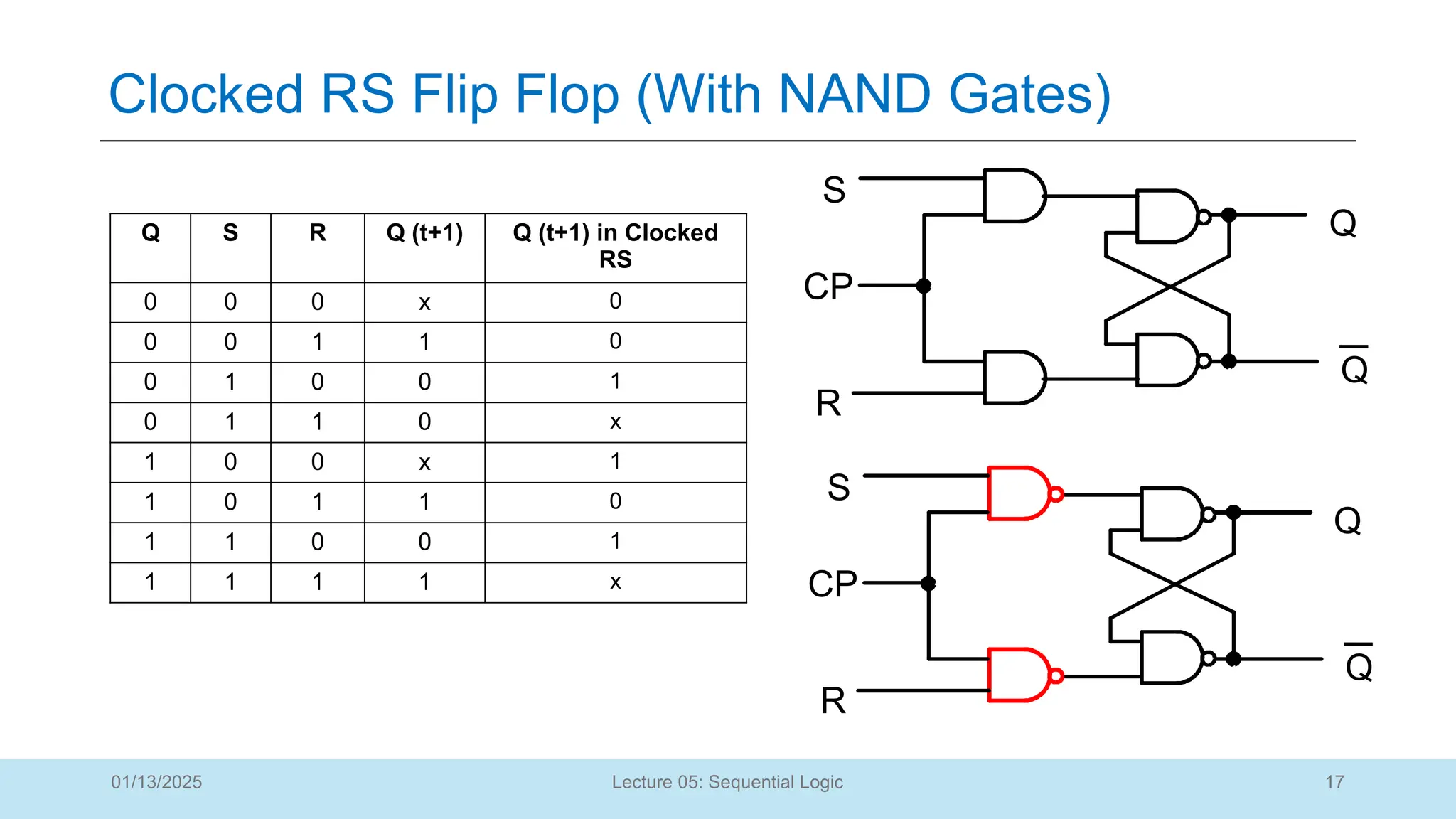
15. 15
Lecture 05: Sequential Logic
Clocked RS Flip Flop
01/13/2025
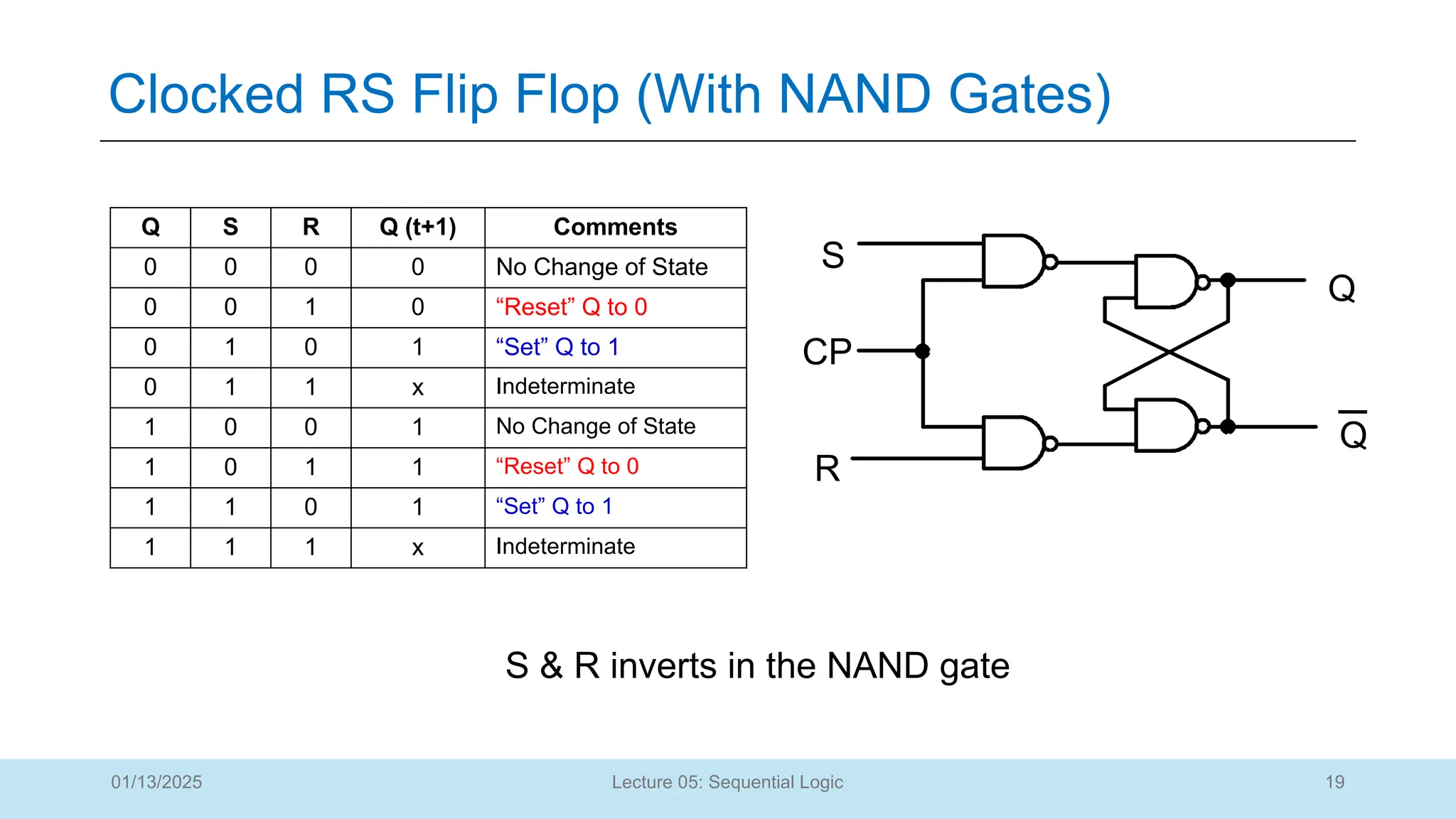
Q S R Q (t+1) Comments
0 0 0 0 No Change of State
0 0 1 0 “Reset” Q to 0
0 1 0 1 “Set” Q to 1
0 1 1 ? Indeterminate
1 0 0 1 No Change of State
1 0 1 0 “Reset” Q to 0
1 1 0 1 “Set” Q to 1
1 1 1 ? Indeterminate
• Adding two NAND gates to the basic S - R
NOR latch gives the clocked RS Latch:
• Has a time sequence behavior similar to the
basic S-R latch except that the S and R
inputs are only observed when the line C is
high.
• The table describes what happens after the
clock [at time (t+1)] based on:
• Present inputs (S,R) and
• Present State Q(t).
• CP means “Clock Pulse”.
• CP=1, S and R has input and the Flip Flop is in
operation
• CP=0, S=R=0;
R
S
Q
CP
Q

16. 16
Lecture 05: Sequential Logic
Clocked RS Flip Flop
01/13/2025
Q S R Q (t+1) Comments
0 0 0 0 No Change of State
0 0 1 0 “Reset” Q to 0
0 1 0 1 “Set” Q to 1
0 1 1 ? Indeterminate
1 0 0 1 No Change of State
1 0 1 0 “Reset” Q to 0
1 1 0 1 “Set” Q to 1
1 1 1 ? Indeterminate
00 01 11 10
0 X 1
1 1 X 1
SR
Q
Q(t+1) = S + R’Q
R
S Q
CP
Q’
R
S
Q
CP
Q

17. 17
Lecture 05: Sequential Logic
Clocked RS Flip Flop (With NAND Gates)
01/13/2025
S
R
Q
CP
Q
Q S R Q (t+1) Q (t+1) in Clocked
RS
0 0 0 x 0
0 0 1 1 0
0 1 0 0 1
0 1 1 0 x
1 0 0 x 1
1 0 1 1 0
1 1 0 0 1
1 1 1 1 x
S
R
Q
CP
Q

18. 18
Lecture 05: Sequential Logic
Clocked RS Flip Flop (With NAND Gates)
01/13/2025
S
R
Q
CP
Q
Q S R Q (t+1) Comments
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

19. 19
Lecture 05: Sequential Logic
Clocked RS Flip Flop (With NAND Gates)
01/13/2025
S
R
Q
CP
Q
Q S R Q (t+1) Comments
0 0 0 0 No Change of State
0 0 1 0 “Reset” Q to 0
0 1 0 1 “Set” Q to 1
0 1 1 x Indeterminate
1 0 0 1 No Change of State
1 0 1 1 “Reset” Q to 0
1 1 0 1 “Set” Q to 1
1 1 1 x Indeterminate
S & R inverts in the NAND gate

20. 20
Lecture 05: Sequential Logic
D Flip Flop
01/13/2025
• Adding an inverter to the S-R Latch,
gives the D Latch: D
Q
C
Q
Q S R Q (t+1) Comments
0 0 0 0 No Change of
State
0 0 1 0 “Reset” Q to 0
0 1 0 1 “Set” Q to 1
0 1 1 ?? Indeterminate
1 0 0 1 No Change of
State
1 0 1 0 “Reset” Q to 0
1 1 0 1 “Set” Q to 1
1 1 1 ?? Indeterminate

21. 21
Lecture 05: Sequential Logic
D Flip Flop
01/13/2025
• Adding an inverter to the S-R Latch,
gives the D Latch:
D
Q
C
Q
Q S R Q (t+1) Comments
0 0 0 0 No Change of State
0 0 1 0 “Reset” Q to 0
0 1 0 1 “Set” Q to 1
0 1 1 ?? Indeterminate
1 0 0 1 No Change of State
1 0 1 0 “Reset” Q to 0
1 1 0 1 “Set” Q to 1
1 1 1 ?? Indeterminate
Q
D
Q (t+1)
D D’
0 0 1 0
0 1 0 1
1 0 1 0
1 1 0 1
Q D Q (t+1)
0 0 0
0 1 1
1 0 0
1 1 1

22. 22
Lecture 05: Sequential Logic
D Flip Flop
01/13/2025
• Adding an inverter to the S-R Latch,
gives the D Latch:
• Note that there are no indeterminate
states
• Input goes to the output with a delay of
one CP
D
Q
C
Q
Q D Q(t+1)
0 0 0
0 1 1
1 0 0
1 1 1 C
D Q
Q
Q(t+1) = D

23. 23
Lecture 05: Sequential Logic
JK Flip Flop
01/13/2025
Q J K Q (t+1) Comments
0 0 0 0 No Change of State
0 0 1 0 “Reset” Q to 0
0 1 0 1 “Set” Q to 1
0 1 1 1 Q’ (Q is complemented)
1 0 0 1 No Change of State
1 0 1 0 “Reset” Q to 0
1 1 0 1 “Set” Q to 1
1 1 1 0 Q’ (Q is complemented)
• A JK Flip Flop is a refinement of the RS Flip Flop
in that the indeterminate states are defined.
• J and K behaves like S and R to SET and CLEAR
the flip flop.
• J for S and K for R
• When both inputs are present, the Flip Flop does not
go to indeterminate state
• Complements Q
K
J
Q
CP
Q

24. 24
Lecture 05: Sequential Logic
JK Flip Flop
01/13/2025
Q J K Q (t+1) Comments
0 0 0 0 No Change of State
0 0 1 0 “Reset” Q to 0
0 1 0 1 “Set” Q to 1
0 1 1 1 Q’
1 0 0 1 No Change of State
1 0 1 0 “Reset” Q to 0
1 1 0 1 “Set” Q to 1
1 1 1 0 Q’
K
J
Q
CP
Q
00 01 11 10
0 1 1
1 1 1
JK
Q
Q(t+1) = JQ’ + K’Q
K
S Q
CP
Q’

25. 25
Lecture 05: Sequential Logic
T Flip Flop
01/13/2025
Q J K Q (t+1)
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0
T
Q
CP
Q

26. 26
Lecture 05: Sequential Logic
T Flip Flop
01/13/2025
Q J K Q (t+1)
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0
T
Q
CP
Q
T Q
CP Q’
Q T Q (t+1)
0 0 0
0 1 1
1 0 1
1 1 0

27. 01/13/2025 Lecture 05: Sequential Logic 27
Topic- 13: Triggering of Flip Flop​

28. 28
Lecture 05: Sequential Logic
Triggering of Flip Flop
01/13/2025
• A flip-flop switches states due to a
trigger, which is a change in the input
signal.
• Types of flip-flop triggering:
 Level Triggering: Triggered by a
constant signal level.
 Edge Triggering: Triggered by a
transition in the signal (positive or
negative edge).
Edge Triggering
Level Triggering

29. 29
Lecture 05: Sequential Logic
Triggering of Flip Flop
01/13/2025
• A clock pulse may be either positive or negative.
• A positive clock source remains at 0 during the interval between pulses and goes to 1 during
the occurrence of a pulse.
• The pulse goes through two signal transitions: from 0 to 1 and the return from 1 to 0.
• As shown in Figure, the positive transition is defined as the positive edge and the negative
transition as the negative edge. This definition applies also to negative pulses

30. 30
Lecture 05: Sequential Logic
Triggering of Flip Flop
01/13/2025
• The clocked flip-flops are triggered during the positive edge of the pulse, and the state
transition starts as soon as the pulse reaches the logic-1 level.
• The new state of the flip-flop may appear at the output terminals while the input pulse is still
1. If the other inputs of the flip-flop change while the clock is still 1, the flip-flop will start
responding to these new values and a new output state may occur.
• When this happens, the output of one flip-flop cannot be applied to the inputs of another flip-
flop when both are triggered by the same clock pulse.
• However, if we can make the flip-flop respond to the positive- (or negative-) edge transition
only, instead of the entire pulse duration, then the multiple-transition problem can be
eliminated.

31. 31
Lecture 05: Sequential Logic
Triggering of Flip Flop
01/13/2025
• One way to make the flip-flop respond only to a pulse transition is to use capacitive coupling.
In this configuration, an RC (resistor-capacitor) circuit is inserted in the clock input of the flip-
flop.
• This circuit generates a spike in response to a momentary change of input signal. A positive
edge emerges from such a circuit with a positive spike, and a negative edge emerges with a
negative spike.
• Edge triggering is achieved by designing the flip-flop to neglect one spike and trigger on the
occurrence of the other spike.
• Another way to achieve edge triggering is to use a master-slave or edge triggered flip-flop.

32. 32
Lecture 05: Sequential Logic
Master-Slave Flip Flop
01/13/2025
• A master-slave flip-flop is constructed from
two separate flip-flops. One circuit serves as
a master and the other as a slave, and the
overall circuit is referred to as a master
slave flip-flop.
• The logic diagram of an RS master-slave
flip-flop is shown in the Figure. It consists of
a master flip-flop, a slave flip-flop, and an
inverter. When clock pulse CP is 0, the
output of the inverter is 1.
• Since the clock input of the slave is 1, the
flip-flop is enabled and output Q is equal to
Y, while Q' is equal to Y '. The master flip-
flop is disabled because CP = 0.
R
S Y
CP
Y’ R
S Q
Q’
Master Slave
S
R
Q
Q’

33. 33
Lecture 05: Sequential Logic
Master-Slave Flip Flop
01/13/2025
• When the pulse becomes 1, the information
then at the external R and S inputs is
transmitted to the master flip-flop.
• The slave flip-flop, however, is isolated as
long as the pulse is at its 1 level, because
the output of the inverter is 0.
• When the pulse returns to 0, the master flip-
flop is isolated, which prevents the external
inputs from affecting it.
• The slave flip-flop then goes to the same
state as the master flip-flop.
R
S Y
CP
Y’ R
S Q
Q’
Master Slave
S
R
Q
Q’

34. 34
Lecture 05: Sequential Logic
Timing Relationships in Master-Slave Flip Flop
01/13/2025
• The timing relationships shown in the Figure illustrate
the sequence of events that occur in a master-slave flip-
flop. Assume that the flip-flop is in the clear state prior to
the occurrence of a pulse, so that Y = 0 and Q = 0. The
input conditions are S = 1, R = 0, and the next clock
pulse should change the flip-flop to the set state with Q =
1.
• During the pulse transition from 0 to 1, the master flip-
flop is set and changes Y to 1. The slave flip-flop is not
affected because its CP input is 0. Since the master flip-
flop is an internal circuit, its change of state is not
noticeable in the outputs Q and Q '. When the pulse
returns to 0, the information from the master is allowed
to pass through to the slave, making the external output
Q = 1.
R
S Y
CP
Y’ R
S Q
Q’
Master Slave
S
R
Q
Q’

35. 35
Lecture 05: Sequential Logic
Timing Relationships in Master-Slave Flip Flop
01/13/2025
• Note that the external S input can be changed at the
same time that the pulse goes through its negative-edge
transition.
• This is because, once the CP reaches 0, the master is
disabled, and its R and S inputs have no influence until
the next clock pulse occurs.
• Thus, in a master-slave flip-flop, it is possible to switch
the output of the flip-flop and its input information with
the same clock pulse. It must be realized that the S input
could come from the output of another master-slave flip-
flop that was switched with the same clock pulse

36. 36
Lecture 05: Sequential Logic
Triggering of Master-Slave JK Flip-Flops
01/13/2025
• A master-slave flip-flop can be
constructed for any type of flip-
flop by adding a clocked RS flip-
flop with an inverted clock to
form the slave.
• An example of a master-slave
JK flip-flop constructed with
NAND gates is shown in the
Figure.
• In the master-slave JK flip-flop
using NAND gates, gates 1-4
form the master flip-flop, while
gates 5-8 form the slave.
Q
Q
CP
J
K
Y
Y
1
2
3
4
5
6
7
8
9
MASTER SLAVE

37. 37
Lecture 05: Sequential Logic
Triggering of Master-Slave JK Flip-Flops
01/13/2025
• Positive Clock Edge:
- The information on the J
and K inputs is transmitted
to the master flip-flop on
the positive edge of a clock
pulse.
- This information is then
held in the master flip-flop
until the negative clock
edge.
Q
Q
CP
J
K
Y
Y
1
2
3
4
5
6
7
8
9
MASTER SLAVE

38. 38
Lecture 05: Sequential Logic
Triggering of Master-Slave JK Flip-Flops
01/13/2025
• Negative Clock Edge:
- At the negative edge, data
passes from the master to
the slave flip-flop, aligning
the slave’s state with the
master.
- The slave flip-flop uses an
inverted clock from gate 9,
isolating it during the
positive clock phase and
allowing it to copy the
master’s state on the
negative clock phase.
Q
Q
CP
J
K
Y
Y
1
2
3
4
5
6
7
8
9
MASTER SLAVE

39. 39
Lecture 05: Sequential Logic
Triggering of Master-Slave JK Flip-Flops
01/13/2025
• Clock Pulse Synchronization
- The clock input is generally
set to 0, keeping gates 1
and 2 at logic level 1,
preventing the J and K
inputs from affecting the
master.
- During the clock’s positive
phase, the master flip-flop
may change states, while
the slave remains isolated.
- When the clock falls back
to 0, the slave flip-flop
mirrors the master’s state.
Q
Q
CP
J
K
Y
Y
1
2
3
4
5
6
7
8
9
MASTER SLAVE

40. 40
Lecture 05: Sequential Logic
System Behaviour with Multiple Master-Slave Flip-Flops
01/13/2025
In a system with multiple synchronized master-slave flip-flops:
• All clock pulses occur simultaneously, ensuring all flip-flops change state in
unison.
• Outputs only change after the clock pulse returns to 0, preventing cascading
effects during state transitions.
• Enables simultaneous data transfer between flip-flops within a single clock
pulse.

41. 41
Lecture 05: Sequential Logic
Edge-Triggered Flip Flop
01/13/2025
• Another type of flip-flop that synchronizes the state changes during a clock-
pulse transition is the edge-triggered flip-flop.
• In this type of flip-flop, output transitions occur at a specific level of the
clock pulse. When the pulse input level exceeds this threshold level, the
inputs are locked out and the flip-flop is therefore unresponsive to further
changes in inputs until the clock pulse returns to 0 and another pulse
occurs.
• Some edge-triggered flip-flops cause a transition on the positive edge of
the pulse, and others cause a transition on the negative edge of the pulse.

42. 42
Lecture 05: Sequential Logic
D-Type Positive Edge-Triggered Flip Flop
01/13/2025
• The logic diagram of a D-type positive-edge-
triggered flip-flop consists of three basic flip-flops.
NAND gates 1 and 2 make up one basic flip-flop and
gates 3 and 4 another.
• The third basic flip-flop comprising gates 5 and 6
provides the outputs to the circuit. Inputs S and R of
the third basic flip-flop must be maintained at logic-1
for the outputs to remain in their steady-state values.
• When S = 0 and R = 1, the output goes to the set
state with Q = 1. When S = 1 and R = 0, the output
goes to the clear state with Q = 0. Inputs Sand R are
determined from the states of the other two basic
flip-flops. These two basic flip flops respond to the
external inputs D (data) and CP (clock pulse)

43. 43
Lecture 05: Sequential Logic
Operation of the 0-Type Edge-Triggered Flip-Flop
01/13/2025
The operation of the circuit is illustrated
through a series of transitions, as shown in
the Figure, which displays gates numbered 1
to 4. These gates demonstrate all possible
states based on clock pulse (CP) and data
(D) inputs. Outputs S and R are obtained
from gates 2 and 3, respectively, which then
feed into additional gates to yield the actual
flip-flop outputs.

44. 44
Lecture 05: Sequential Logic
Operation of the 0-Type Edge-Triggered Flip-Flop
01/13/2025
The clock pulse (CP) is set to 0, which affects the output behavior of the flip-flop in a specific way:
• Inputs and Initial State:
 CP = 0 is applied to all gates, essentially disabling any changes in output states.
 D (Data) input can be either 0 or 1, but due to CP being 0, this input does not affect the flip-
flop's outputs.
• Gate Configurations:
 Gate 1 and Gate 4 have their inputs influenced by the value of D:
 When D=0, Gate 4 outputs 1, causing Gate 1 to output 0.
 When D=1, Gate 4 outputs 0, causing Gate 1 to output 1.
 Gates 2 and 3:
 Since CP = 0, the outputs of both Gate 2 and Gate 3 are set to 1, resulting in S = 1 and R
= 1.
• Steady-State Condition:
 With S = 1 and R = 1, the flip-flop is held in a steady state.
 No changes in the output occur, regardless of the D input, because CP = 0 prevents any
transition.

45. 45
Lecture 05: Sequential Logic
Operation of the 0-Type Edge-Triggered Flip-Flop
01/13/2025
The clock pulse (CP) is set to 1, allowing the flip-flop to respond to changes in the D input and
transition between states.
• Inputs and Initial State:
 CP = 1 enables the flip-flop to react to the D input, allowing changes in output states.
 D input (0 or 1) now directly influences the flip-flop's behavior, thanks to CP = 1.
• Gate Configurations:
 Gate 1 and Gate 4:
 When D=0, Gate 4 outputs 1, causing Gate 1 to output 0.
 When D=1, Gate 4 outputs 0, causing Gate 1 to output 1.
 Gates 2 and 3 respond to these configurations, determining the values of S and R:
 If D = 0: The circuit sets S = 0 and R = 1, representing one possible state of the flip-flop.
 If D = 1: The circuit sets S = 1 and R = 0, representing an alternative flip-flop state.
• Edge-Triggered Operation:
 With CP = 1, the flip-flop is "enabled" and can change states based on the value of D.
 This configuration demonstrates the edge-triggered characteristic, where the flip-flop’s output
states only change during the active clock pulse.

46. 01/13/2025 Lecture 05: Sequential Logic 46
Topic- 14: Analysis of Clocked Sequential
Circuit

47. 47
Lecture 05: Sequential Logic
Analysis of Clocked Sequential Circuit
01/13/2025
Combinational
Logic
Memory
Elements
Inputs Outputs
Present
State
Next
State
• General Model
• Current State at time (t) is stored in an array
of flip-flops.
• Next State at time (t+1) is a Boolean
function of State and Inputs.
• Outputs at time (t) are a Boolean function of
State (t) and (sometimes) Inputs (t).

48. 48
Lecture 05: Sequential Logic
Analysis of Clocked Sequential Circuit
01/13/2025
A
C
D Q
Q
C
D Q
Q
y
x A
B
CP
Input x
Output y
Present State A,
A(t+1) = x A + x B
B(t+1) = x A’
y = x‘ ( B + A )
Logic Diagram Output Equation

49. 49
Lecture 05: Sequential Logic
State Table
01/13/2025
• State table – a multiple variable table with the following four sections:
• Present State – the values of the state variables for each allowed state.
• Input – the input combinations allowed.
• Next-state – the value of the state at time (t+1) based on the present state
and the input.
• Output – the value of the output as a function of the present state and
(sometimes) the input.
• From the viewpoint of a truth table:
• the inputs are Input, Present State
• and the outputs are Output, Next State

50. 50
Lecture 05: Sequential Logic
State Table Representation - 1
01/13/2025
Present State Input Next State Output
A B x A(t+1) B(t+1) y
0
1
0
1
0
1
0
1
Input x
Output y
Present State A, B
A(t+1) = x A + x B
B(t+1) = x A’
y = x‘ ( B + A )
Output Equation State Table

51. 51
Lecture 05: Sequential Logic
State Table Representation - 1
01/13/2025
Present State Input Next State Output
A B x A(t+1) B(t+1) y
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 0 0 1
0 1 1 1 1 0
1 0 0 0 0 1
1 0 1 1 0 0
1 1 0 0 0 1
1 1 1 1 0 0
Input x
Output y
Present State A, B
A(t+1) = x A + x B
B(t+1) = x A’
y = x‘ ( B + A )
Output Equation State Table

52. 52
Lecture 05: Sequential Logic
State Table Representation - 2
01/13/2025
Present
State
Next State
x=0 x=1
Output
x=0 x=1
A B y(t) y(t)
0 0 0 0 0 1 0 0
0 1 0 0 1 1 1 0
1 0 0 0 1 0 1 0
1 1 0 0 1 0 1 0
A B A B
State Table
Present State Input Next State Output
A B x A(t+1) B(t+1) y
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 0 0 1
0 1 1 1 1 0
1 0 0 0 0 1
1 0 1 1 0 0
1 1 0 0 0 1
1 1 1 1 0 0

53. 53
Lecture 05: Sequential Logic
State Diagram
01/13/2025
• The sequential circuit function can be represented in graphical form as a state
diagram with the following components:
• A circle with the state name in it for each state
• A directed arc from the Present State to the Next State for each state
transition
• A label on each directed arc with the Input values which causes the state
transition, and
• A label:
• On each circle with the output value produced, or
• On each directed arc with the output value produced.

54. 54
Lecture 05: Sequential Logic
State Diagram
01/13/2025
Present
State
Next State
x = 0 x = 1
Output
x = 0 x = 1
A B y(t) y(t)
0 0 0 0 0 1 0 0
0 1 0 0 1 1 1 0
1 0 0 0 1 0 1 0
1 1 0 0 1 0 1 0
A B A B
State Table State Diagram

55. 55
Lecture 05: Sequential Logic
State Diagram
01/13/2025
A B
0 0
0 1 1 1
1 0
0/1 1/0
1/0
1/0
0/1
0/1
1/0
0/0
Present
State
Next State
x = 0 x = 1
Output
x = 0 x = 1
A B y(t) y(t)
0 0 0 0 0 1 0 0
0 1 0 0 1 1 1 0
1 0 0 0 1 0 1 0
1 1 0 0 1 0 1 0
A B A B
State Table State Diagram

56. 56
Lecture 05: Sequential Logic
State Equation
01/13/2025
Present State Input Next State Output
A B x A(t+1) B(t+1) y
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 0 0 1
0 1 1 1 1 0
1 0 0 0 0 1
1 0 1 1 0 0
1 1 0 0 0 1
1 1 1 1 0 0
State Table

57. 57
Lecture 05: Sequential Logic
An Example of a Sequential Circuit
01/13/2025
CP
B’
R Q’
S Q
A
x'
x
x
x'
A’
B’
B
B
A’
R Q’
S Q
A
A
x
B’
y
Presen
t State
Next State Output
x=0 x=1 x=0 x=1
A B A B A B y y
Logic Diagram State Table
At A=0, B=0, x=0
0
0
0
0
0
0
0
0
0
0
= 0
= 0
= 0

58. 58
Lecture 05: Sequential Logic
An Example of a Sequential Circuit
01/13/2025
CP
B’
R Q’
S Q
A
x'
x
x
x'
A’
B’
B
B
A’
R Q’
S Q
A
A
x
B’
y
Logic Diagram State Table
Presen
t State
Next State Output
x=0 x=1 x=0 x=1
A B A B A B y y
0 0 0 0 0 1 0 0
0 1 1 1 0 1 0 0
1 0 1 0 0 0 0 1
1 1 1 0 1 1 0 0

59. 59
Lecture 05: Sequential Logic
An Example of a Sequential Circuit
01/13/2025
A B
0 0
0 1 1 1
1 0
1/1 0/0
0/0
1/0
0/0
0/0
1/0
1/0
Prese
nt
State
Next State Output
x=0 x=1 x=0 x=
1
A B A B A B y y
0 0 0 0 0 1 0 0
0 1 1 1 0 1 0 0
1 0 1 0 0 0 0 1
1 1 1 0 1 1 0 0
State Table State Diagram

60. 60
Lecture 05: Sequential Logic
An Example of a Sequential Circuit
01/13/2025
Presen
t State
Next State Output
x=0 x=1 x=0 x=1
A B A B A B y y
0 0 0 0 0 1 0 0
0 1 1 1 0 1 0 0
1 0 1 0 0 0 0 1
1 1 1 0 1 1 0 0
Present
State
Inpu
t
Next
State
Outpu
t
A B x A B y
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 1 1 0
0 1 1 0 1 0
1 0 0 1 0 0
1 0 1 0 0 1
1 1 0 1 0 0
1 1 1 1 1 0
Illustration of the Table for optimization (optional)

61. 61
Lecture 05: Sequential Logic
An Example of a Sequential Circuit
01/13/2025
Present
State
Inpu
t
Next
State
Output
A B x A B y
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 1 1 0
0 1 1 0 1 0
1 0 0 1 0 0
1 0 1 0 0 1
1 1 0 1 0 0
1 1 1 1 1 0
00 01 11 10
0 1
1 1 1 1
Bx
A
A(t+1) = Bx’ + AB + Ax’
= Bx’ + (B + x’)A
= Bx’ + (B’x)’A
00 01 11 10
0 1 1 1
1 1
Bx
A
B(t+1) = A’x + A’B + Bx
= A’x + (A’ + x)B
= Bx’ + (Ax’)’B

62. 62
Lecture 05: Sequential Logic
Exercise 6-11 (Morris Mano)
01/13/2025
A Sequential circuit has four (04) flip-flops A, B, C, D. It is described by following state
equations:
A(t+1) = (CD’+C’D)x + (CD+C’D’)x’
B(t+1) = A
C(t+1) = B
D(t+1) = C
Obtain the sequence of States when x = 1, starting from state ABCD = 0001
Obtain the sequence of States when x = 0, starting from state ABCD = 0000

63. 63
Lecture 05: Sequential Logic
Exercise 6-11 (Morris Mano)
01/13/2025
Present State Input Next State Output
A B x A(t+1) B(t+1) y
0
1
0
1
0
1
0
1
Input x
Output y
Present State A, B
A(t+1) = x A + x B
B(t+1) = x A’
y = x‘ ( B + A )
Output Equation State Table
Output Equation

64. 01/13/2025 Lecture 05: Sequential Logic 64
Topic- 15: State Reduction and Assignment

65. 65
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
a
b
d
f
c
e
g
0/0
1/0
0/0
0/0
1/0 1/0
0/0
1/1
0/0
1/1
0/0
1/1
0/0
1/1

66. 66
Lecture 05: Sequential Logic
State Reduction
01/13/2025
a
b
d
f
c
e
g
0/0
1/0
0/0
0/0
1/0 1/0
0/0
1/1
0/0
1/1
0/0
1/1
0/0
1/1
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1

67. 67
Lecture 05: Sequential Logic
State Reduction
01/13/2025
a
b
d
f
c
e
g
0/0
1/0
0/0
0/0
1/0 1/0
0/0
1/1
0/0
1/1
0/0
1/1
0/0
1/1
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1
 Two states are said to be equivalent if,
• for each member of the set of inputs, they give exactly
same output.

68. 68
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1
For example
 State g and State e
• They go to the same next state a when
x=0 and f when x=1
• They give same output 0 when x=0 and 1
when x=1
e
 State g and State e are equivalent
 g can be replaced by e.

69. 69
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e d 0 1
e a d 0 1
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f d 0 1
e a f d 0 1
f g e f 0 1
g a f 0 1

70. 70
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e d 0 1
e a d 0 1
a
b
d
c
e
0/0
1/0
0/0
0/0
1/0
1/0
0/0
1/1
0/0
1/1
Reduced State Diagram Reduced State

71. 71
Lecture 05: Sequential Logic
State Reduction
01/13/2025
a
b
d
f
c
e
g
0/0
1/0
0/0
0/0
1/0 1/0
0/0
1/1
0/0
1/1
0/0
1/1
0/0
1/1
State a a b
Input 0 1 0 1 0 1 1 0 1 0 0
Output 0 0
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1

72. 72
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1
a
b
d
f
c
e
g
0/0
1/0
0/0
0/0
1/0 1/0
0/0
1/1
0/0
1/1
0/0
1/1
0/0
1/1
State a a b c d e f f g f g a
Input 0 1 0 1 0 1 1 0 1 0 0
Output 0 0 0 0 0 1 1 0 1 0 0

73. 73
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e d 0 1
e a d 0 1
a
b
d
c
e
0/0
1/0
0/0
0/0
1/0
1/0
0/0
1/1
0/0
1/1
Reduced State Diagram
Reduced State Table

74. 74
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e d 0 1
e a d 0 1
State a a b c d e d d e d e a
Input 0 1 0 1 0 1 1 0 1 0 0
Output 0 0 0 0 0 1 1 0 1 0 0
Output Sequence with Reduced
State Table
Reduced State Table

75. 75
Lecture 05: Sequential Logic
State Reduction
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e d 0 1
e a d 0 1
Same Output Sequence
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1
State a a b c d e f f g f g a
Input 0 1 0 1 0 1 1 0 1 0 0
Output 0 0 0 0 0 1 1 0 1 0 0

76. 76
Lecture 05: Sequential Logic
Class Work
01/13/2025
Question-2: The state table of a sequential circuit is given below. Reduce the states to minimum
possible states. Draw the reduced state diagram (the state diagram before reduction is not
required). Also find the output sequence of the reduced state generated with an input sequence
01110010011..
Present
State
Next State Output
x=0 x=1 x=0 x=1
a f b 0 0
b d c 0 0
c f e 0 0
d g a 1 0
e d c 0 0
f f b 1 1
g g h 0 1

77. Lecture 05: Sequential Logic 77
Present
State
Next State Output
x=0 x=1 x=0 x=1
a f b 0 0
b d c 0 0
c f e 0 0
d g a 1 0
e d c 0 0
f f b 1 1
g g h 0 1
h g a 1 0
Present
State
Next State Output
x=0 x=1 x=0 x=1
a f b 0 0
b d a 0 0
d g a 1 0
f f b 1 1
g g d 0 1
d
d
b
b
a
a
Reduced State Table
Class Work
01/13/2025

78. Present
State
Next State Output
x=0 x=1 x=0 x=1
a f b 0 0
b d a 0 0
d g a 1 0
f f b 1 1
g g d 0 1
Reduced State Table
Reduced State Diagram
a
b
d
f
g 0/1
1/
0
1/
1
0/
0
0/
0 1/
1
0/
1
1/
1
1/
0
0/
0
78
01/13/2025 Lecture 05: Sequential Logic
Class Work

79. Presen
t State
Next
State
Output
x=0 x=1 x=0 x=1
a f b 0 0
b d a 0 0
d g a 1 0
f f b 1 1
g g d 0 1
Reduced State Table
Output Sequence
State a f b a b d g d g g d a
Input 0 1 1 1 0 0 1 0 0 1 1
Output 0 1 0 0 0 1 1 1 0 1 0
79
01/13/2025 Lecture 05: Sequential Logic
Class Work

80. State Assignments
State Assignment-1 Assignment-2 Assignment-3
a 001 000 000
b 010 010 100
c 011 011 010
d 100 100 101
e 101 100 011
• Binary value of the states are immaterial as long as they are unique and
sequence maintains proper input/output relationship.
80
01/13/2025 Lecture 05: Sequential Logic

81. Excitation Table - SR
Q S R Q (t+1)
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 x
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 x
S R Q (t+1)
0 0 Q(t)
0 1 0
1 0 1
1 1 x
Q Q (t+1) S R
0 0 0 0
0 0 0 1
0 1 1 0
0 x 1 1
1 1 0 0
1 0 0 1
1 1 1 0
1 x 1 1
Q Q (t+1) S R
0 0 0 x
0 1 1 0
1 0 0 1
1 1 x 0
Q Q (t+1) S R
0 0 0 x
0 1 1 0
1 0 0 1
1 1 x 0
81
01/13/2025 Lecture 05: Sequential Logic

82. Excitation Table
S R Q (t+1)
0 0 Q(t)
0 1 0
1 0 1
1 1 ??
Q Q (t+1) S R
0 0 0 x
0 1 1 0
1 0 0 1
1 1 x 0
J K Q (t+1)
0 0 Q(t)
0 1 0
1 0 1
1 1 Q’(t)
Q Q (t+1) J K
0 0 0 x
0 1 1 x
1 0 x 1
1 1 x 0
D Q (t+1)
0 0
1 1
Q Q (t+1) D
0 0 0
0 1 1
1 0 0
1 1 1
T Q (t+1)
0 Q(t)
1 Q’(t)
Q Q (t+1) T
0 0 0
0 1 1
1 0 1
1 1 0
SR Flip Flop
JK Flip Flop
D Flip Flop
T Flip Flop
82
01/13/2025 Lecture 05: Sequential Logic

83. 01/13/2025 Lecture 05: Sequential Logic 83
Topic- 16: Design Procedure

84. 84
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
1. Problem Specification
• Word description of the circuit behavior
• May have a state diagram, timing diagram, etc.
2. Formulation - Obtain a state diagram or state table
3. Reduction of states, if necessary
4. State Assignment - Assign binary codes to the states
5. Determine the number of Flip-Flops
6. Choose the type of Flip Flops
7. Derive circuit excitation and output equation or table
8. Optimization - Optimize the equations
9. Draw the Logic diagram

85. 85
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Present
State
Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1
a
b
d
f
c
e
g
0/0
1/0
0/0
0/0
1/0 1/0
0/0
1/1
0/0
1/1
0/0
1/1
0/0
1/1
Step-1 : Problem Specification Step-2 : Formulation (State Table)

86. 86
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Present State Next State Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e d 0 1
e a d 0 1
Presen
t State
Next
State
Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1
Step-2 : State Table Step-3 : Reduction of State Table

87. 87
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Present State Next State Output
x=0 x=1 x=0 x=1
a 001 a b 0 0
b 010 c d 0 0
c 011 a d 0 0
d 100 e d 0 1
e 101 a d 0 1
Present
State
Next
State
Output
x=0 x=1 x=0 x=1
a a b 0 0
b c d 0 0
c a d 0 0
d e f 0 1
e a f 0 1
f g f 0 1
g a f 0 1
Step-2 : State Table Step-3 : Reduction of State Table
Step-4 : Assign Binary Values to States

88. 88
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Present State Input Next State Flip Flop Inputs Output
A B C x A B C SA RA SB RB SC RC y
0 0 1 0 0 0 1 0 X 0 X X 0 0
0 0 1 1 0 1 0
0 1 0 0 0 1 1
0 1 0 1 1 0 0
0 1 1 0 0 0 1
0 1 1 1 1 0 0
1 0 0 0 1 0 1
1 0 0 1 1 0 0
1 0 1 0 0 0 1
1 0 1 1 1 0 0
Step-5 : Number of FF Step-6 : Type of FF = SR Step-7 : Excitation Table
Q Q (t+1) S R
0 0 0 x
0 1 1 0
1 0 0 1
1 1 x 0

89. 89
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Present State Input Next State Flip Flop Inputs Output
A B C x A B C SA RA SB RB SC RC y
0 0 1 0 0 0 1 0 X 0 X X 0 0
0 0 1 1 0 1 0 0 X 1 0 0 1 0
0 1 0 0 0 1 1 0 X X 0 1 0 0
0 1 0 1 1 0 0 1 0 0 1 0 X 0
0 1 1 0 0 0 1 0 X 0 1 X 0 0
0 1 1 1 1 0 0 1 0 0 1 0 1 0
1 0 0 0 1 0 1 X 0 0 X 1 0 0
1 0 0 1 1 0 0 X 0 0 X 0 X 1
1 0 1 0 0 0 1 0 1 0 X X 0 0
1 0 1 1 1 0 0 X 0 0 X 0 1 1
Step-5 : Number of FF Step-6 : Type of FF = SR Step-7 : Excitation Table

90. 90
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Step-8 : Optimization and FF Functions
00 01 11 10
00 X X
01 1 1
11 X X X X
10 X X X
Cx
AB
SA = Bx
Present State Input Flip Flop Inputs
A B C x SA
0 0 1 0 0
0 0 1 1 0
0 1 0 0 0
0 1 0 1 1
0 1 1 0 0
0 1 1 1 1
1 0 0 0 X
1 0 0 1 X
1 0 1 0 0
1 0 1 1 X
States 0000, 0001, 1100,
1101, 1110, 1111 are not
present and can be
considered don’t care

91. 91
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Step-8 : Optimization and FF Functions
Similarly
SA = Bx RA = Cx’
SB = A’B’x RB = BC + Bx
SC = x’ RC = x
Y = Ax

92. 92
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Step-8 : Logic Diagram
SA = Bx
RA = Cx’
SB = A’B’x
RB = BC +
Bx
SC = x’
RC = x
Y = Ax
A
Q
Q’
RA
SA
x
CP
Q
Q’
RB
SB
Q
Q’
RC
SC
B
C
y

93. 93
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
0
00
10
11
01 0
0
1
1
1
1
0
Input
Combinations Next
State
Output Combination
Present
State
Input Flip Flop Inputs
A B x A B JA KA JB KB
0 0 0 0 0 0 x 0 x
0 0 1 0 1 0 x 1 x
0 1 0 1 0
0 1 1 0 1
1 0 0 1 0
1 0 1 1 1
1 1 0 1 1
1 1 1 0 0
Q Q (t+1) J K
0 0 0 x
0 1 1 x
1 0 x 1
1 1 x 0

94. 94
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Input Combination
Next State
Output Combination
Present
State
Input Flip Flop Inputs
A B x A B JA KA JB KB
0 0 0 0 0 0 x 0 x
0 0 1 0 1 0 x 1 x
0 1 0 1 0 1 x x 1
0 1 1 0 1 0 x x 0
1 0 0 1 0 x 0 0 x
1 0 1 1 1 x 0 1 x
1 1 0 1 1 x 0 x 0
1 1 1 0 0 x 1 x 1
0
00
10
11
01 0
0
1
1
1
1
0

95. 95
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Input Combinations
Next State
Output Combination
Present
State
Input Flip Flop Inputs
A B x A B JA KA JB KB
0 0 0 0 0 0 x 0 x
0 0 1 0 1 0 x 1 x
0 1 0 1 0 1 x x 1
0 1 1 0 1 0 x x 0
1 0 0 1 0 x 0 0 x
1 0 1 1 1 x 0 1 x
1 1 0 1 1 x 0 x 0
1 1 1 0 0 x 1 x 1
00 01 11 10
0 1
1 x x x x
Bx
A
JA = Bx’
Similarly
JA = Bx’
KA = Bx
JB = x
KB = (A  x)’

96. 96
Lecture 05: Sequential Logic
Design Procedure
01/13/2025
Output Equations
JA = Bx’ KA = Bx
JB = x KB = (A  x)’ B
KB
JB
Q
Q’
A
KA
JA
x
CP
Q
Q’

97. 97
Lecture 05: Sequential Logic
Design Procedure (Class Work)
01/13/2025
Problem:
Analyze the given state diagram of a clocked
sequential circuit and find the (i) state table (ii)
state equation and (iii) logic diagram. Consider J-
K Flip Flop for the logic diagram of the sequential
circuit.
Input Combination
Next State
Outp
ut
Present State Input
A B x A B y
(I) STATE TABLE

98. 98
Lecture 05: Sequential Logic
Design Procedure (Class Work)
01/13/2025
Problem:
Analyze the given state diagram of a clocked
sequential circuit and find the (i) state table (ii)
state equation and (iii) logic diagram. Consider J-
K Flip Flop for the logic diagram of the sequential
circuit.
(I) STATE TABLE
Input Combination
Next State
Outp
ut
Present State Input
A B x A B y
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 1 1 0
0 1 1 0 1 0
1 0 0 1 0 1
1 0 1 1 1 1
1 1 0 1 0 0
1 1 1 1 1 0

99. 99
Lecture 05: Sequential Logic
Design Procedure (Class Work)
01/13/2025
Input
Combination
Next
State
Output
Combination Ou
tp
ut
Present
State
Inp
ut
Flip Flop Inputs
A B x A B JA KA JB KB y
0 0 0 0 0 0
0 0 1 0 1 0
0 1 0 1 1 0
0 1 1 0 1 0
1 0 0 1 0 1
1 0 1 1 1 1
1 1 0 1 0 0
1 1 1 1 1 0
Input
Combination Next
State
Output
Combination Out
put
Present
State
Inp
ut
Flip Flop Inputs
A B x A B JA KA JB KB y
0 0 0 0 0 0 x 0 x 0
0 0 1 0 1 0 x 1 x 0
0 1 0 1 1 1 x x 1 0
0 1 1 0 1 0 x x 0 0
1 0 0 1 0 x 0 0 x 1
1 0 1 1 1 x 0 1 x 1
1 1 0 1 0 x 0 x 0 0
1 1 1 1 1 x 1 x 1 0
EXCITATION TABLE (Required for State equation)

100. 100
Lecture 05: Sequential Logic
Design Procedure (Class Work)
01/13/2025
Excitation Table for JK
Q Q (t+1) J K
0 0 0 x
0 1 1 x
1 0 x 1
1 1 x 0
Input
Combinations Next
State
Output
Combination Out
put
Present
State
Inp
ut
Flip Flop Inputs
A B x A B JA KA JB KB y
0 0 0 0 0 0 X 0 X 0
0 0 1 0 1 0 X 1 X 0
0 1 0 1 1 1 X X 0 0
0 1 1 0 1 0 X X 0 0
1 0 0 1 0 X 0 0 X 1
1 0 1 0 0 X 1 0 X 1
1 1 0 1 0 X 0 X 1 0
1 1 1 1 1 X 0 X 0 0

101. 101
Lecture 05: Sequential Logic
Design Procedure (Class Work)
01/13/2025
Bx
A 00 01 11 10
0 1
1 x x x x
JA = Bx’
Bx
A 00 01 11 10
0 x x x x
1 1
KA = B’x
Input
Combinations Next
State
Output
Combination Out
put
Present
State
Inp
ut
Flip Flop Inputs
A B x A B JA KA JB KB y
0 0 0 0 0 0 0 X 0 X 0
1 0 0 1 0 1 0 X 1 X 0
2 0 1 0 1 1 1 X X 0 0
3 0 1 1 0 1 0 X X 0 0
4 1 0 0 1 0 X 0 0 X 1
5 1 0 1 0 0 X 1 0 X 1
6 1 1 0 1 0 X 0 X 1 0
7 1 1 1 1 1 X 0 X 0 0

102. 102
Lecture 05: Sequential Logic
Design Procedure (Class Work)
01/13/2025
Bx
A 00 01 11 10
0 1 x x
1 x x
JB = A’x
Bx
A 00 01 11 10
0 x x
1 x x 1
KB = Ax’
Y = AB’
Input
Combinations Next
State
Output
Combination Out
put
Present
State
Inp
ut
Flip Flop Inputs
A B x A B JA KA JB KB y
0 0 0 0 0 0 0 X 0 X 0
1 0 0 1 0 1 0 X 1 X 0
2 0 1 0 1 1 1 X X 0 0
3 0 1 1 0 1 0 X X 0 0
4 1 0 0 1 0 X 0 0 X 1
5 1 0 1 0 0 X 1 0 X 1
6 1 1 0 1 0 X 0 X 1 0
7 1 1 1 1 1 X 0 X 0 0

103. 103
Lecture 05: Sequential Logic
Design Procedure (Class Work)
01/13/2025
Y = AB’
JB = A’x
KB = Ax’
Y = AB’
JA = Bx’
KA = B’x
B
KB
JB
Q
Q’
A
KA
JA
x
CP
Q
Q’
A’
B’
Y

104. 01/13/2025 Lecture 05: Sequential Logic 104
Topic- 17: Design of Counters

105. 105
Lecture 05: Sequential Logic
Design of Counters
01/13/2025
• A sequential circuit that goes through a prescribed sequence of states upon the
application of input pulses is called a counter.
• The input pulses, called count pulses, may be clock pulses or they may
originate from an external source and may occur at prescribed intervals of time
or at random.
• In a counter, the sequence of states may follow a binary count or any other
sequence of states.
• Counters are found in almost all equipment containing digital logic. They are
used for counting the number of occurrences of an event and are useful for
generating timing sequences to control operations in a digital system.

106. 106
Lecture 05: Sequential Logic
Design of Counters
01/13/2025
000
100
001
010
011
110
101
111
Count
Sequence
Flip Flop
Inputs
A B C TA TB TC
0 0 0 0 0 1
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
Q Q (t+1) T
0 0 0
0 1 1
1 0 1
1 1 0
State Diagram
Excitation Table for T-FF
Excitation Table for Counter
Design with T-FF

107. 107
Lecture 05: Sequential Logic
Design of Counters
01/13/2025
000
100
001
010
011
110
101
111
Count
Sequence
Flip Flop
Inputs
A B C TA TB TC
0 0 0 0 0 1
0 0 1 0 1 1
0 1 0 0 0 1
0 1 1 1 1 1
1 0 0 0 0 1
1 0 1 0 1 1
1 1 0 0 0 1
1 1 1 1 1 1
Q Q (t+1) T
0 0 0
0 1 1
1 0 1
1 1 0
State Diagram
Excitation Table for T-FF
Excitation Table for Counter
Design with T-FF

108. 108
Lecture 05: Sequential Logic
Design of Counters
01/13/2025
Simplification by
Observation
TA = BC
TB = C
TC = 1
T Q
T Q
CP
A
B
T Q
C
1
Count
Sequence
Flip Flop
Inputs
A B C TA TB TC
0 0 0 0 0 1
0 0 1 0 1 1
0 1 0 0 0 1
0 1 1 1 1 1
1 0 0 0 0 1
1 0 1 0 1 1
1 1 0 0 0 1
1 1 1 1 1 1

109. 109
Lecture 05: Sequential Logic
Example
01/13/2025
Problem:
Design a sequential circuit with four FFs A, B, C & D. The next state of B, C &
D are equal to the present state of A, B, & C. The next state of A is the X-OR
of the present state of C & D.
Boolean illustration of the
Problem Statement:
• A (t+1) = C  D
• B (t+1) = A
• C (t+1) = B
• D (t+1) = C
Solution
• It is a Shift Register (present state of A, B, & C
goes to B, C &D)
• It has a controlled feedback to A (i.e. C  D)
• Simplest plan is to use D-FF
• DA = C  D
• DB = A
• DC = B
• DD = C

110. 110
Lecture 05: Sequential Logic
Example
01/13/2025
Problem:
Design a sequential circuit with JK – FF satisfying following equations
• A (t+1) = A’B’CD + A’B’C + ACD + AC’D’
• B (t+1) = A’C + CD’ + A’B’C
• C (t+1) = B
• D (t+1) = D’
Solution
• The characteristics equation of JK – FF is Q(t+1) = JQ’+K’Q
• Transform all equations in the above format

111. 111
Lecture 05: Sequential Logic
Example
01/13/2025
A (t+1) = A’B’CD + A’B’C + ACD + AC’D’
= (B’CD + B’C) A’ + (CD + C’D’)
A
= (J) A’ + (K’) A
JA = B’CD +
B’C
= B’C (D+1)
= B’C
KA = (CD +
C’D’)’ = C’D + CD’
= C  D
B (t+1) = A’C + CD’ + A’BC’
= (A’C + CD’) + (A’C’) B
= (A’C + CD’) (B’+B) + (A’C’) B
= (A’C + CD’) B’ + (A’C + CD’+A’C’) B
= (J) B’ + (K’) B
JB = A’C + CD’
KB = (A’C + CD’+A’C)’
= (A’(C + C’) + CD’)’
= (A’ + CD’)’
= (A’C+A’D’)’
= AC’ + AD

112. 112
Lecture 05: Sequential Logic
Example
01/13/2025
C (t+1) = B
= B(C’+C)
= BC’ + BC
= (J)C’ + (K’) C
JC = B
KC = B’
D (t+1) = D’
= 1.D’ + 0.D
= (J) D’ + (K’) D
JD = 1
KD = (0)’
= 1

113. 113
Lecture 05: Sequential Logic
Example
01/13/2025
Draw the Circuit
JA = B’C KA = C  D
JB = A’C + CD’ KB = AC’ + AD
JC = B KC = B’
JD = 1 KD = 1

114. 114
Lecture 05: Sequential Logic
Exercise
01/13/2025
• Practice the following examples from book:
 Example 6-1
 Example 6-2
 Example 6-3
 Example 6-4
 Example 6-5