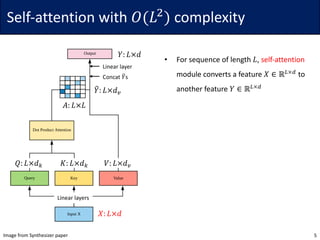
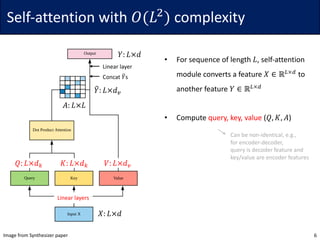
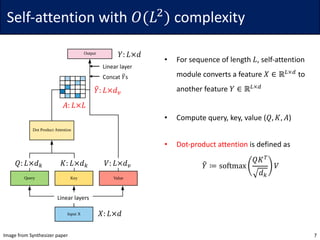
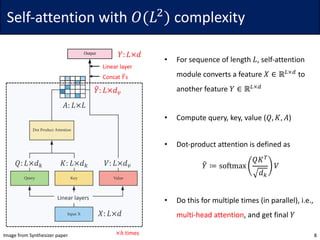
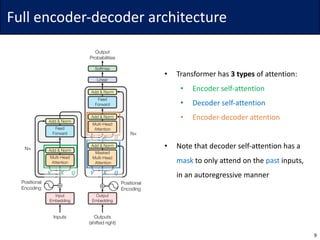
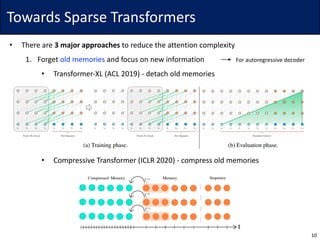
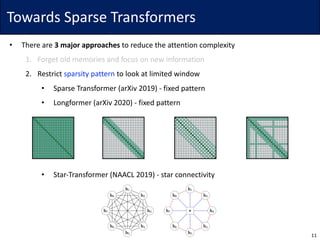
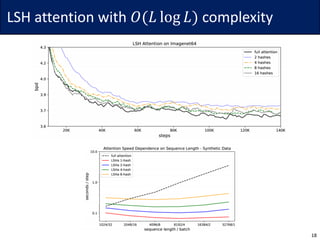
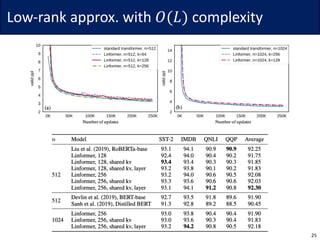
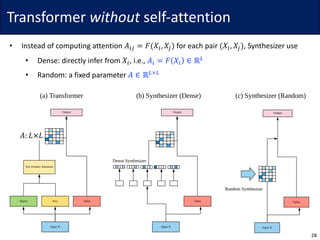
This document summarizes research on reducing the computational complexity of self-attention in Transformer models from O(L2) to O(L log L) or O(L). It describes the Reformer model which uses locality-sensitive hashing to achieve O(L log L) complexity, the Linformer model which uses low-rank approximations and random projections to achieve O(L) complexity, and the Synthesizer model which replaces self-attention with dense or random attention. It also briefly discusses the expressive power of sparse Transformer models.

1. 1
Self-Attention with Linear Complexity
ALIN-LAB @ KAIST - Paper Review Seminar
2020.06.24.
Sangwoo Mo

2. Outline
1. Transformer: 𝑂(𝐿$
) complexity of self-attention
2. Reformer: 𝑂(𝐿 log 𝐿) approximation
3. Linformer: 𝑂(𝐿) approximation
4. Synthesizer: Transformer without self-attention
5. (+1) Expressivity: Are sparse Transformers sufficiently powerful?
2

3. Outline
1. Transformer: 𝑂(𝐿$
) complexity of self-attention
2. Reformer: 𝑂(𝐿 log 𝐿) approximation
3. Linformer: 𝑂(𝐿) approximation
4. Synthesizer: Transformer without self-attention
5. (+1) Expressivity: Are sparse Transformers sufficiently powerful?
3

4. Transformer (NeurIPS 2017)
4

5. Self-attention with 𝑂(𝐿$
) complexity
5
𝑋: 𝐿×𝑑
𝑄: 𝐿×𝑑. 𝐾: 𝐿×𝑑. 𝑉: 𝐿×𝑑1
𝐴: 𝐿×𝐿
Linear layers
𝑌: 𝐿×𝑑
• For sequence of length 𝐿, self-attention
module converts a feature 𝑋 ∈ ℝ6×7
to
another feature 𝑌 ∈ ℝ6×7
Image from Synthesizer paper
𝑌8: 𝐿×𝑑1
Linear layer
Concat 𝑌8s

6. Self-attention with 𝑂(𝐿$
) complexity
6
𝑋: 𝐿×𝑑
𝑄: 𝐿×𝑑. 𝐾: 𝐿×𝑑. 𝑉: 𝐿×𝑑1
𝐴: 𝐿×𝐿
Linear layers
𝑌: 𝐿×𝑑
• For sequence of length 𝐿, self-attention
module converts a feature 𝑋 ∈ ℝ6×7
to
another feature 𝑌 ∈ ℝ6×7
• Compute query, key, value (𝑄, 𝐾, 𝐴)
Image from Synthesizer paper
𝑌8: 𝐿×𝑑1
Linear layer
Concat 𝑌8s
Can be non-identical, e.g.,
for encoder-decoder,
query is decoder feature and
key/value are encoder features

7. Self-attention with 𝑂(𝐿$
) complexity
7
𝑋: 𝐿×𝑑
𝑄: 𝐿×𝑑. 𝐾: 𝐿×𝑑. 𝑉: 𝐿×𝑑1
𝐴: 𝐿×𝐿
𝑌8: 𝐿×𝑑1
Linear layers
𝑌: 𝐿×𝑑
• For sequence of length 𝐿, self-attention
module converts a feature 𝑋 ∈ ℝ6×7
to
another feature 𝑌 ∈ ℝ6×7
• Compute query, key, value (𝑄, 𝐾, 𝐴)
• Dot-product attention is defined as
𝑌8 ≔ softmax
𝑄𝐾A
𝑑.
𝑉
Image from Synthesizer paper
Linear layer
Concat 𝑌8s

8. Self-attention with 𝑂(𝐿$
) complexity
8
𝑋: 𝐿×𝑑
𝑄: 𝐿×𝑑. 𝐾: 𝐿×𝑑. 𝑉: 𝐿×𝑑1
𝐴: 𝐿×𝐿
Linear layers
Linear layer
𝑌: 𝐿×𝑑
• For sequence of length 𝐿, self-attention
module converts a feature 𝑋 ∈ ℝ6×7
to
another feature 𝑌 ∈ ℝ6×7
• Compute query, key, value (𝑄, 𝐾, 𝐴)
• Dot-product attention is defined as
𝑌8 ≔ softmax
𝑄𝐾A
𝑑.
𝑉
• Do this for multiple times (in parallel), i.e.,
multi-head attention, and get final 𝑌
Image from Synthesizer paper
Concat 𝑌8s
×ℎ times
𝑌8: 𝐿×𝑑1

9. Full encoder-decoder architecture
9
• Transformer has 3 types of attention:
• Encoder self-attention
• Decoder self-attention
• Encoder-decoder attention
• Note that decoder self-attention has a
mask to only attend on the past inputs,
in an autoregressive manner𝐾 𝑄𝑉 𝐾 𝑄𝑉
𝐾 𝑄𝑉

10. Towards Sparse Transformers
• There are 3 major approaches to reduce the attention complexity
1. Forget old memories and focus on new information
• Transformer-XL (ACL 2019) - detach old memories
• Compressive Transformer (ICLR 2020) - compress old memories
10
For autoregressive decoder

11. Towards Sparse Transformers
• There are 3 major approaches to reduce the attention complexity
1. Forget old memories and focus on new information
2. Restrict sparsity pattern to look at limited window
• Sparse Transformer (arXiv 2019) - fixed pattern
• Longformer (arXiv 2020) - fixed pattern
• Star-Transformer (NAACL 2019) - star connectivity
11

12. Towards Sparse Transformers
• There are 3 major approaches to reduce the attention complexity
1. Forget old memories and focus on new information
2. Restrict sparsity pattern to look at limited window
3. Learn sparsity pattern using extra components
• Adaptive Span Transformer (ACL 2019) - binary mask
• Reformer (ICLR 2020) - locally sensitive hashing
• Routing Transformer (arXiv 2020) - 𝑘-means clustering
• BP-Transformer (arXiv 2019) - bipartite partitioning
12

13. Outline
1. Transformer: 𝑂(𝐿$
) complexity of self-attention
2. Reformer: 𝑂(𝐿 log 𝐿) approximation
3. Linformer: 𝑂(𝐿) approximation
4. Synthesizer: Transformer without self-attention
5. (+1) Expressivity: Are sparse Transformers sufficiently powerful?
13

14. Reformer (ICLR 2020)
• Propose two tricks to improve the efficiency of Transformer
• Locality-sensitive hashing (LSH) to reduce the complexity of self-attention
• Reversible residual layers to reduce the memory of feed-forward layer
• We only focus on the LSH attention part here
14

15. LSH attention with 𝑂(𝐿 log 𝐿) complexity
15
• Since query and key are identical for self-attention, the authors set 𝑄 = 𝐾
• This additional constraint does not degrade the performance
• One can define the similarity of indices thanks to the symmetry
=

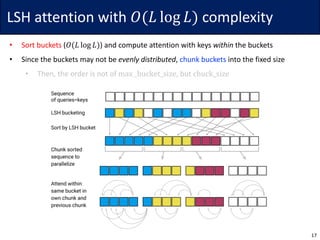
16. LSH attention with 𝑂(𝐿 log 𝐿) complexity
16
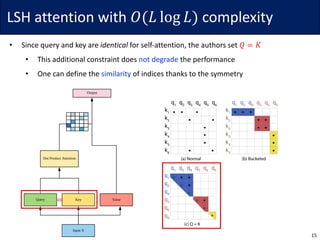
• Idea: For each query 𝑞G, consider only the closest subset of keys
• Since softmax is dominated by the largest elements, it may be sufficient
• To find the nearest neighbors, the authors use locally sensitive hashing (LSH)
• The hash function ℎ maps similar vector 𝑥 to similar bucket ℎ 𝑥 ∈ {0, … , 𝑏 − 1}
• The vectors should be evenly distributed, i.e., the size of buckets should be similar
• Define ℎ 𝑥 = arg max([𝑥𝑅; −𝑥𝑅]) for a (fixed) random matrix 𝑅 ∈ ℝ7V×W/$
Andoni et al. Practical and optimal LSH for angular distance. NeurIPS 2015.

17. LSH attention with 𝑂(𝐿 log 𝐿) complexity
17
• Sort buckets (𝑂(𝐿 log 𝐿)) and compute attention with keys within the buckets
• Since the buckets may not be evenly distributed, chunk buckets into the fixed size
• Then, the order is not of max _bucket_size, but chuck_size

18. LSH attention with 𝑂(𝐿 log 𝐿) complexity
18

19. Outline
1. Transformer: 𝑂(𝐿$
) complexity of self-attention
2. Reformer: 𝑂(𝐿 log 𝐿) approximation
3. Linformer: 𝑂(𝐿) approximation
4. Synthesizer: Transformer without self-attention
5. (+1) Expressivity: Are sparse Transformers sufficiently powerful?
19

20. Linformer (NeurIPS 2020 submission)
20

21. Low-rank approx. with 𝑂(𝐿) complexity
• For 𝑄, 𝐾 ∈ ℝ6×7
for 𝑑 ≪ 𝐿, the attention 𝐴 = softmax 𝑄𝐾A
∈ ℝ6×6
≈ low-rank
• Note that 𝐴d ≔ 𝑄𝐾A
is rank 𝑑, but 𝐴 is not due to the non-linearity of softmax
• Instead, one may apply random projection (Johnson-Lindenstrauss, or JL lemma)
that 𝑃𝑅A
𝑅𝑤A
≈ 𝑃𝑤A
for gaussian vector 𝑅 ∈ ℝ.×6
for 𝑘 = Ω(log 𝐿)
• Experiments show that 𝐴 is approximately low-rank
• 𝐿 = 512 and 𝑑 = 128, but rank is not exactly 128
21

22. Low-rank approx. with 𝑂(𝐿) complexity
• For 𝑄, 𝐾 ∈ ℝ6×7
for 𝑑 ≪ 𝐿, the attention 𝐴 = softmax 𝑄𝐾A
∈ ℝ6×6
≈ low-rank
• Note that 𝐴d ≔ 𝑄𝐾A
is rank 𝑑, but 𝐴 is not due to the non-linearity of softmax
• Instead, one may apply random projection (Johnson-Lindenstrauss, or JL lemma)
that 𝑃𝑅A
𝑅𝑤A
≈ 𝑃𝑤A
for gaussian vector 𝑅 ∈ ℝ.×6
for 𝑘 = Ω(log 𝐿)
• There are two challenges in naively applying low-rank approx. for 𝐴
1. How to reduce 𝑘 = Ω(1)?
2. How to get low-rank 𝐴hij ≈ 𝐴 ∈ ℝ6×6
, e.g., without costly SVD?
• Contribution:
1. Using the property rank 𝐴d = 𝑑, the authors reduce 𝑘 = Θ log 𝑑
2. Instead of SVD, the authors reduce 𝐴 ∈ ℝ6×.
, 𝑉 ∈ ℝ.×6
to compute 𝑌8
22

23. Low-rank approx. with 𝑂(𝐿) complexity
23
• Apply projection 𝐸, 𝐹 ∈ ℝ6×.
to 𝐾, 𝑉,
respectively; now the attention is given by
𝑌8 ≔ softmax
𝑄 ⋅ 𝐾A
𝐸
𝑑.
𝐹A
𝑉

24. Low-rank approx. with 𝑂(𝐿) complexity
24
• Apply projection 𝐸, 𝐹 ∈ ℝ6×.
to 𝐾, 𝑉,
respectively; now the attention is given by
𝑌8 ≔ softmax
𝑄 ⋅ 𝐾A
𝐸
𝑑.
𝐹A
𝑉
• Applying JL lemma to a submatrix of size Θ(𝑑)
instead of the original matrix size 𝑂(𝐿), one
can approx. the output with 𝑘 = Θ(log 𝑑)
• In practice, the authors learn 𝐸, 𝐹 instead of
random projection (but share parameters)

25. Low-rank approx. with 𝑂(𝐿) complexity
25

26. Outline
1. Transformer: 𝑂(𝐿$
) complexity of self-attention
2. Reformer: 𝑂(𝐿 log 𝐿) approximation
3. Linformer: 𝑂(𝐿) approximation
4. Synthesizer: Transformer without self-attention
5. (+1) Expressivity: Are sparse Transformers sufficiently powerful?
26

27. Synthesizer (NeurIPS 2020 submission)
27

28. Transformer without self-attention
• Instead of computing attention 𝐴Gp = 𝐹(𝑋G, 𝑋p) for each pair (𝑋G, 𝑋p), Synthesizer use
• Dense: directly infer from 𝑋G, i.e., 𝐴G = 𝐹 𝑋G ∈ ℝ6
• Random: a fixed parameter 𝐴 ∈ ℝ6×6
28
𝐴: 𝐿×𝐿

29. Transformer without self-attention
• Surprisingly, this synthesized attention show comparable results in many NLP tasks
• It works well for machine translation, language modeling, and text generation
• However, it does not work well for natural language understanding (NLI)
• Remark: This is because the attention of former ones are aligned (i.e., diagonal-like),
but NLI needs more complex attention structure
29

30. Outline
1. Transformer: 𝑂(𝐿$
) complexity of self-attention
2. Reformer: 𝑂(𝐿 log 𝐿) approximation
3. Linformer: 𝑂(𝐿) approximation
4. Synthesizer: Transformer without self-attention
5. (+1) Expressivity: Are sparse Transformers sufficiently powerful?
30

31. Expressive power of (sparse) Transformers
• Universal approximation of Transformers (ICLR 2020)
• Universal approximation of sparse Transformers (NeurIPS 2020 submission)
31

32. Universal approx. for Transformers
• Definition. Let 𝒯r,s,t
be a family of Transformers without positional encoding (PE) that
has ℎ heads of size 𝑚 each, and feed-forward layer with 𝑟 hidden nodes
• Definition. Let 𝒯w
r,s,t
be a family of Transformers with PE such that
𝒯w
r,s,t
≔ {𝑔w 𝑿 = 𝑔 𝑿 + 𝑬 ∣ 𝑔 ∈ 𝒯r,s,t
, 𝑬 ∈ ℝ7×6
}
32

33. Universal approx. for Transformers
• Definition. Let 𝒯r,s,t
be a family of Transformers without positional encoding (PE) that
has ℎ heads of size 𝑚 each, and feed-forward layer with 𝑟 hidden nodes
• Definition. Let 𝒯w
r,s,t
be a family of Transformers with PE such that
𝒯w
r,s,t
≔ {𝑔w 𝑿 = 𝑔 𝑿 + 𝑬 ∣ 𝑔 ∈ 𝒯r,s,t
, 𝑬 ∈ ℝ7×6
}
• Theorem 1. Transformer without PE, specifically 𝑔 ∈ 𝒯$,},~
, can approximate any
permutation equivariant function 𝑓 ∈ ℱw•
• Theorem 2. Transformer with PE, specifically 𝑔w ∈ 𝒯w
$,},~
, can approximate any
continuous seq2seq function (in compact domain) 𝑓 ∈ ℱ‚ƒ
• Remark: It is nontrivial since self-attention is pair-wise and shared among layers
33

34. Universal approx. for Transformers
• Theorem 1. Transformer without positional encoding (PE), specifically 𝑔 ∈ 𝒯$,},~
,
can approximate any permutation equivariant function 𝑓 ∈ ℱw•
• Proof sketch:
1. Approx. 𝑓 ∈ ℱw• with piece-wise constant function 𝑓̅ ∈ ℱ…w•
• Classical result in analysis
2. Approx. 𝑓̅ ∈ ℱ…w• with modified Transformer 𝑔̅ ∈ 𝒯…$,},}
such that
• Softmax → Max / ReLU → piece-wise linear activation 𝝓 with ≤ 3 pieces
1. Approx. modified Transformer 𝑔̅ ∈ 𝒯…$,},}
with original Transformer 𝑔 ∈ 𝒯$,},~
• Approx. 𝜙 with 4 ReLUs (hence 𝒯…$,},}
→ 𝒯$,},~
)
34
Main contribution

35. Universal approx. for Transformers
• Lemma 1.1. Approx. 𝑓̅ ∈ ℱ…w• with modified Transformer 𝑔̅ ∈ 𝒯…$,},}
• Softmax → Max / ReLU → piece-wise linear activation 𝝓 with ≤ 3 pieces
• Proof sketch:
1. Convert input 𝑿 to a quantized set 𝑳 with a series of feed-forward layers
• piece-wise linear activation 𝝓 with ≤ 3 pieces condition is used here
2. Convert 𝑳 to a distinct embedding 𝑞(𝑳) with a series of self-attention layers
• Max operation condition is used here
3. Convert 𝑞(𝑳) to the desired output of 𝑓̅ with a series of feed-forward layers
35
Main contribution

36. Universal approx. for Transformers
• Lemma 1.1. Approx. 𝑓̅ ∈ ℱ…w• with modified Transformer 𝑔̅ ∈ 𝒯…$,},}
• Lemma 1.2. Convert 𝑳 to a distinct embedding 𝑞(𝑳) with a series of self-attention layers
• Definition. A mapping 𝑞: 𝕃 ⊂ ℝ7×6
→ ℝ}×6
is contextual embedding if it satisfies
1. For any 𝑳 ∈ 𝕃, all 𝐿 entries of q(𝑳) are distinct
2. For any 𝑳 ≠ 𝑳•
∈ 𝕃, all 𝐿 entries of q(𝑳) and q(𝑳•
) are distinct
• Namely, the contextual embedding maps all sets/entries in distinct space
36

37. Universal approx. for Transformers
• Lemma 1.1. Approx. 𝑓̅ ∈ ℱ…w• with modified Transformer 𝑔̅ ∈ 𝒯…$,},}
• Lemma 1.2. Convert 𝑳 to a distinct embedding 𝑞(𝑳) with a series of self-attention layers
• Proof sketch:
• Using two attention heads of size 1, one can implement selective shift operation,
which shifts the entries in a specific interval, while leaving all others intact
• Recall: 𝑔̅ is a modified Transformer using Max operation and 𝝓 activation
• Concretely, the attention is given by 𝒁 → 𝒁 + Ψ 𝒁; 𝑏, 𝑏•
where
• Stacking this operation, one can construct the contextual embedding 𝑞
37

38. Universal approx. for Transformers
• Theorem 2. Transformer with PE, specifically 𝑔w ∈ 𝒯w
$,},~
, can approximate any
continuous seq2seq function (in compact domain) 𝑓 ∈ ℱ‚ƒ
• Proof sketch:
• For 𝑿 ∈ 0,1 7×6
, define positional encoding 𝐸 as follows:
• Then, columns are monotonically increasing for all rows
• Following similar steps, one can express any continuous seq2seq functions
38

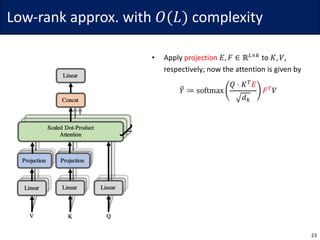
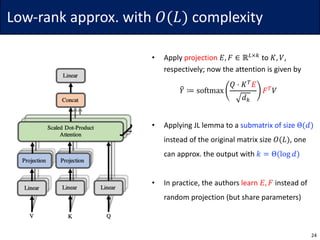
39. Universal approx. for sparse Transformers
• Definition. Let {𝒜.
“
} be a sparsity pattern of 𝑘-th token for 𝑙 ∈ 𝑝 ≔ {1,2, … , 𝑝}
• Dense Transformer: 𝑝 = 1, 𝒜.
}
= [𝑛] for all 𝑘 ∈ [𝑛]
• Theorem 3. If sparsity pattern satisfies the following:
• it can approximate any continuous seq2seq function (in compact domain)
• Proof sketch:
• Due to the assumption, every index
can be connected as the layer goes
39

40. Universal approx. for sparse Transformers
• Definition. Let {𝒜.
“
} be a sparsity pattern of 𝑘-th token for 𝑙 ∈ 𝑝 ≔ {1,2, … , 𝑝}
• Theorem 3. If sparsity pattern satisfies the following:
• it can approximate any continuous seq2seq function (in compact domain)
• In particular, the following architectures satisfy the condition:
• Sparse Transformer - 𝑂(𝐿˜/$
) connections
• Star-Transformer - 𝑂(𝐿) connections
• Longformer - 𝑂(𝐿) connections
40

41. Discussion
• Linformer reduce the complexity of self-attention from 𝑂(𝐿$
) to 𝑂(𝐿)
• However, there are several remaining questions:
1. Empirical performance
• While Linformer has the best provable complexity, other architectures (e.g.,
Reformer or non-provable methods) may show the better performance
(especially, for the problems with moderately long sequences)
• We may need extensive comparison of numerous Transformer architectures
2. Expressive power
• It is unclear if Reformer and Linformer are expressive as the dense Transformer
• It is hard to apply Yun et al. since they do not assume a fixed sparsity pattern
41

42. Thank you for listening!