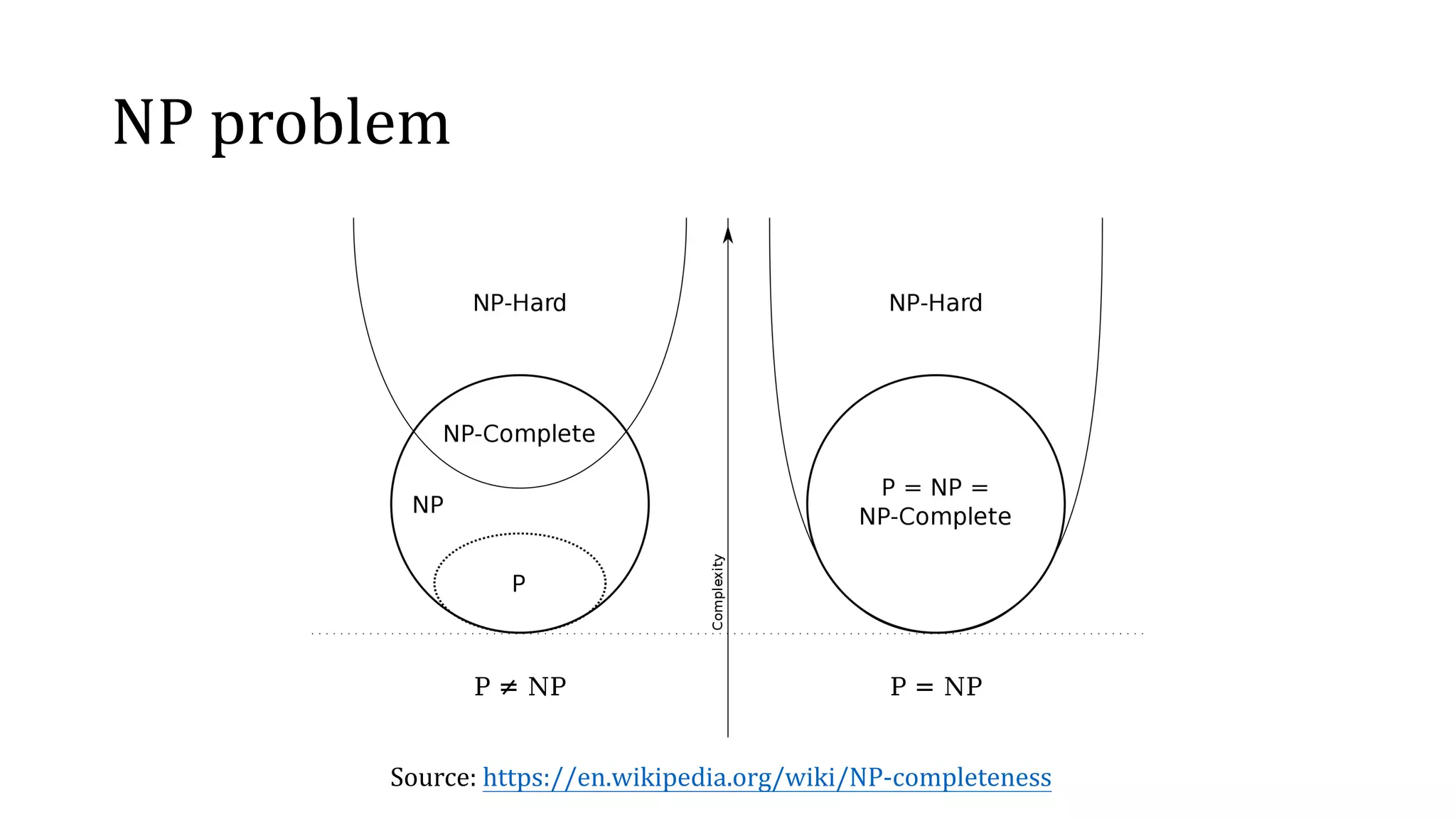
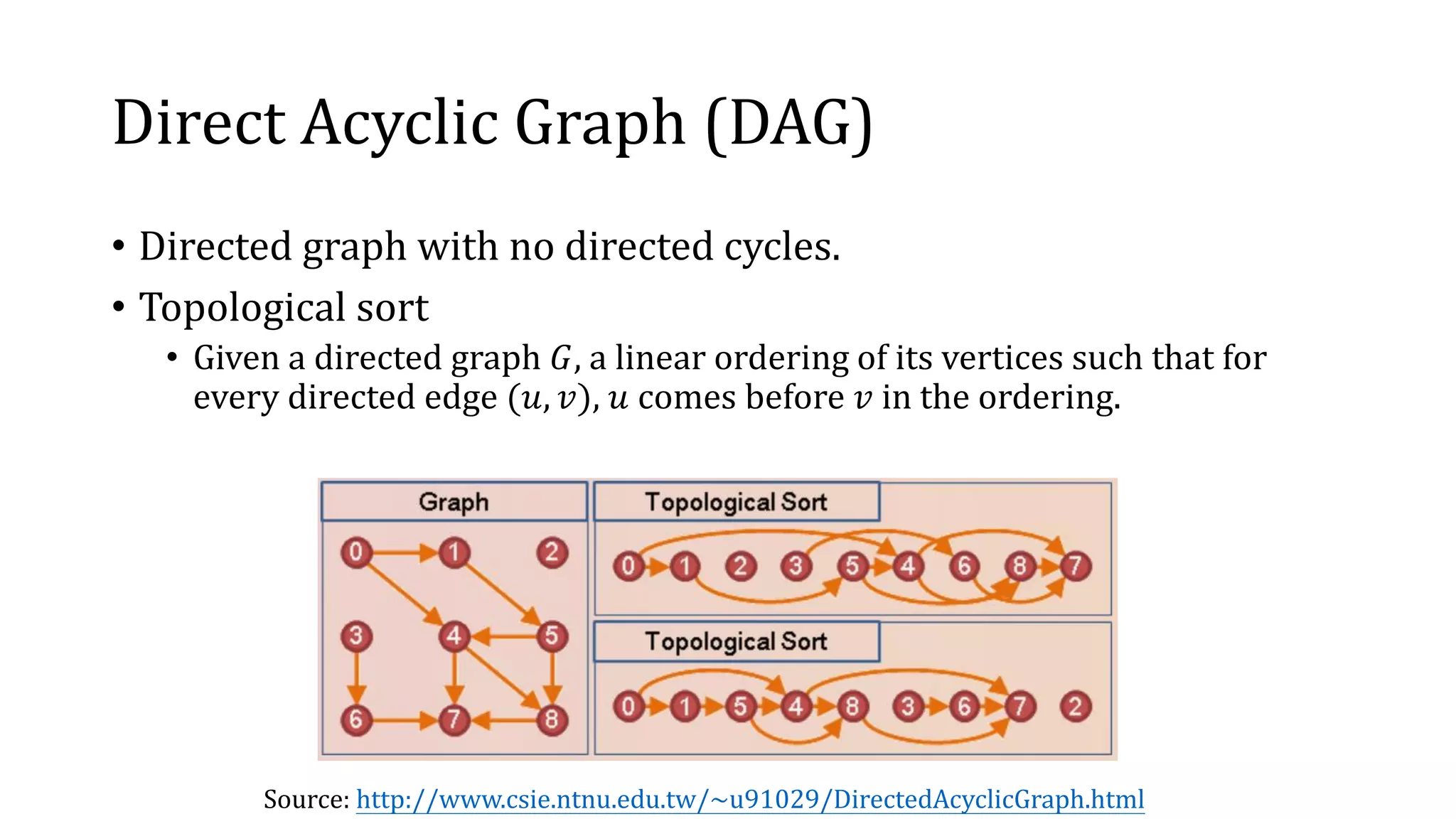
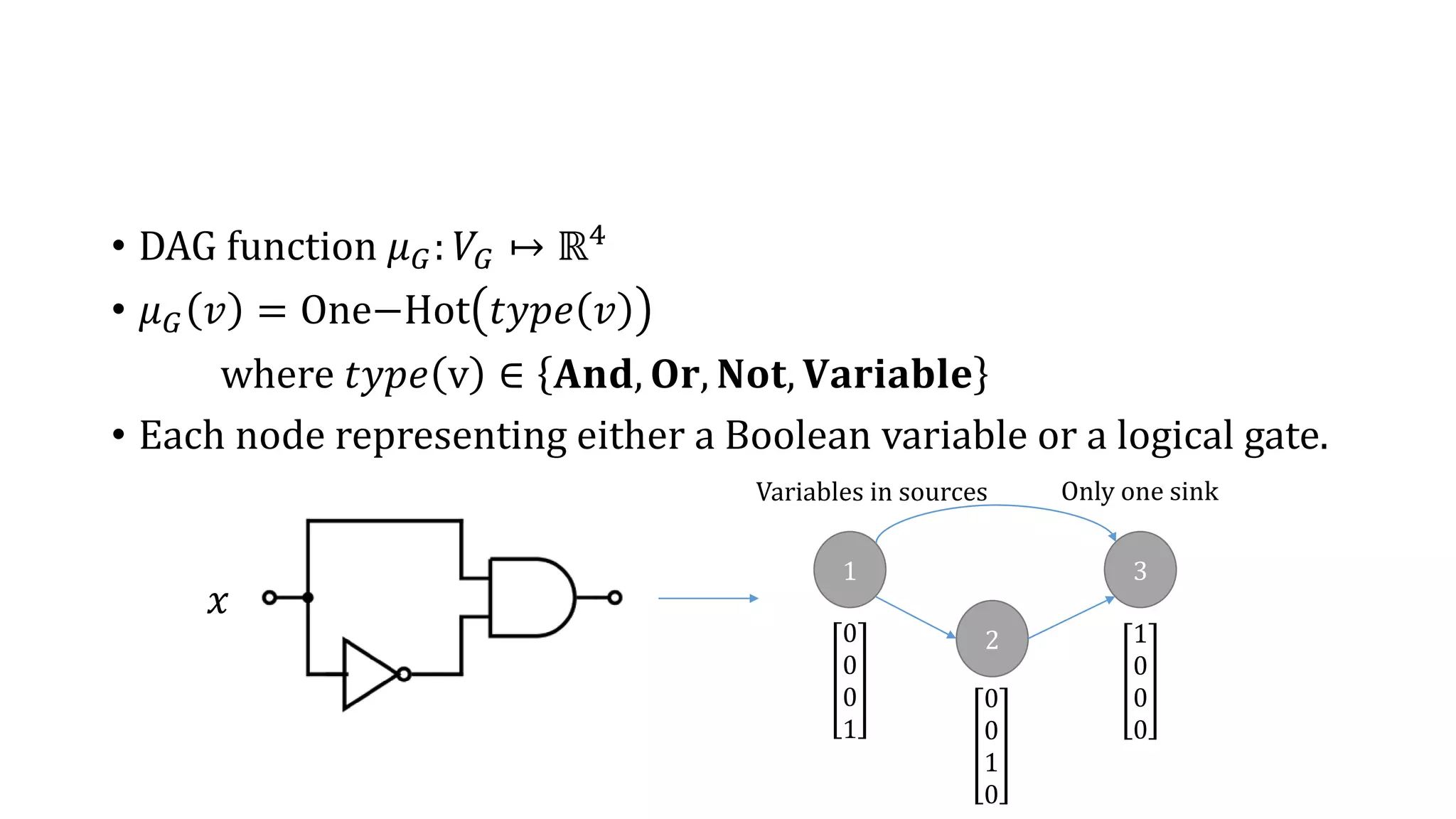
The document presents a neural framework designed to solve the circuit-satisfiability (circuit-sat) problem using a differentiable approach and a directed acyclic graph embedding. It highlights the advantages of this model over the neurosat method, showcasing greater out-of-sample generalization performance while addressing the inherent structures of combinatorial optimization problems. Experimental results demonstrate the model's effectiveness in generating solutions for various Boolean circuits with improved efficiency compared to traditional methods.

1. Learning to Solve Circuit-SAT:
an Unsupervised
Differentiable Approach
Saeed Amizadeh, Sergiy Matusevych and Markus Weimer
Microsoft
ICLR 2019

2. Outline
• Abstract
• Introduction
• Background
• DAG embedding
• Application to the Circuit-SAT problem
• Experimental evaluation
• Discussion

3. Abstract
• New trend of applying rich neural architectures to solve classical
combinatorial optimization problems.
• Propose a neural framework that can learn to solve the Circuit-SAT
problem.
• Rich embedding architecture that encode the problem structure
• Differentiable training procedure that mimics RL
• Train the model directly toward solving the SAT problem
• Show the superior out-of-sample generalization performance
compared to NeuroSAT method.

4. Introduction

5. • The emergence of neural models for learning how to solve the
classical combinatorial optimization problems.
• In practice, for a given class of combinatorial problems, the
problem instances are typically drawn from a certain (unknown)
distribution.
• If there are sufficient number of problem instances, ML (DL) is
capable of extracting the common structures among these
instances and produce models that would outperform the carefully
hand-crafted algorithms.

6. • Supervised learning
• Be shown to be effective for various NP-complete problems.
• The resulted model is bounded by greedy strategy (sub-optimal in
general).
• Reinforcement learning
• Learn the optimal decision and search heuristics beyond the greedy
strategy.
• Challenging work to train such model.
• Propose a neural Circuit-SAT training the model directly toward
the end goal.

7. Represent the instance
• Classical architectures like RNNs or LSTMs
• Ignore the inherent structure present in the problem instances.
• Neural graph embedding embraces the information on graph that
represents the problem structure.
• Most methods synchronously propagate local information on an
underlying graph.
• The information is propagated sequentially rather than
synchronously in the proposed model.

8. Background

9. NP problem
Source: https://en.wikipedia.org/wiki/NP-completeness

10. SAT
• The problem of determining if there exists an assignment that satisfies
a given Boolean formula (consisted of variable, AND, OR and NOT).
• E.g.
• 𝑢1 ∨ ¬𝑢2 ∧ (¬𝑢1 ∨ 𝑢2)
• 𝑢1 = 𝑢2 = TRUE → SAT
• Variable: 𝑢1, 𝑢2
• Literals: 𝑢1, ¬𝑢1, 𝑢2, ¬𝑢2
• Clauses: 𝑢1 ∨ ¬𝑢2 , (¬𝑢1 ∨ 𝑢2)
• Conjunctive normal form (CNF)
• Conjunction (AND) of one or more clauses, where a clause is a disjunction (OR)
of literals.
Source: https://en.wikipedia.org/wiki/Conjunctive_normal_form

11. Circuit-SAT
• The decision problem of determining whether a given Boolean
circuit (only composed of AND, OR and NOT gate) has an
assignment of its inputs that makes the output true.
Source : https://en.wikipedia.org/wiki/Circuit_satisfiability_problem
𝒙 𝟏 𝒙 𝟐 𝒚
0 0 0
0 1 0
1 0 0
1 1 1
𝒙 𝒚
0 0
1 0
𝑥1
𝑥2
𝑦 𝑦𝑥
SAT UNSAT

12. NeuroSAT (Selsam et al. (2018))
• Approach the SAT problem as a binary classification problem.
• Find the SAT solution by clustering the latent representation
extracted from the learned classifier.
• NOT directly trained toward finding SAT solutions.
Source: https://github.com/dselsam/neurosat

13. Direct Acyclic Graph (DAG)
• Directed graph with no directed cycles.
• Topological sort
• Given a directed graph 𝐺, a linear ordering of its vertices such that for
every directed edge (𝑢, 𝑣), 𝑢 comes before 𝑣 in the ordering.
Source: http://www.csie.ntnu.edu.tw/~u91029/DirectedAcyclicGraph.html

14. DAG embedding

15. • DAG 𝐺 = 𝑉𝐺, 𝐸 𝐺
• Reversed DAG 𝐺 𝑟
with the same set of nodes but reversed edges
• For 𝑣 ∈ 𝑉𝐺, 𝜋 𝐺(𝑣) represents the set of direct predecessors
• DAG function 𝜇 𝐺: 𝑉𝐺 ↦ ℝ 𝑑
• Define 𝒢 𝑑 as the space of all possible 𝑑-dimensional functions 𝜇 𝐺
• Model ℱ 𝜃 𝜇 𝐺 = 𝒞 𝒶(𝒫(ℰℬ(𝜇 𝐺)))
• Embedding function ℰℬ: 𝒢 𝑑
↦ 𝒢 𝑞
• Pooling function 𝒫: 𝒢 𝑞
↦ 𝒢 𝑞
• Retrieve only the sink nodes in the input DAG
• Classification function 𝒞 𝒶: 𝒢 𝑞
↦ 𝒪

16. • For simplicity, define
• Feature vector 𝒙 𝑣 = 𝜇 𝐺 𝑣 ∈ ℝ 𝑑
• State vector 𝒉 𝑣 = 𝛿 𝐺 𝑣 ∈ ℝ 𝑞 where 𝛿 𝐺: 𝑉𝐺 ↦ ℝ 𝑞
• Update logic that applying on each node:
𝒉 𝑣 = 𝐺𝑅𝑈 𝒙 𝑣, 𝒉 𝑣
′
, where 𝒉 𝑣
′
= 𝒜({𝒉 𝑢|𝑢 ∈ 𝜋(𝑣)})
• Aggregator function 𝒜: 2 𝑉 𝐺 ↦ ℝ 𝑞
• Aggregate state of node’s direct predecessors.
• Apply the update logic sequentially in the topological sort order.

17. Deep-Gated DAG Recursive Neural
Network (DG-DAGRNN)
• Stack 𝐿-layer embedding layer where the 𝑖th layer has its own parameters ℬ𝑖
and output DAG function dimensionality 𝑞𝑖.
• Apply sequentially 𝑇 times on stacked 𝐿 layers.
ℰℬ 𝜇 𝐺 ≡ ℰℬ
𝑇
𝜇 𝐺 , where ℰℬ
𝑡
𝜇 𝐺 = ℰ 𝑠𝑡𝑎𝑐𝑘 𝑃𝑟𝑜𝑗 𝑯 ℰℬ
𝑡−1
𝜇 𝐺 , ∀𝑡 ∈ 2. . 𝑇
ℰℬ
1
𝜇 𝐺 = ℰ 𝑠𝑡𝑎𝑐𝑘(𝜇 𝐺)
s. t. ℰ 𝑠𝑡𝑎𝑐𝑘 = ℰℬ 𝐿
∘ ℰℬ 𝐿−1
∘ ℰ1
• 𝑤ℎ𝑒𝑟𝑒 ℬ = 〈ℬ1, … , ℬ 𝐿, 𝑯〉 is the list of parameters and 𝑃𝑟𝑜𝑗 𝑯: 𝒢 𝑞 𝐿 ↦ 𝒢 𝑑 is the
linear projection with the projection matrix 𝑯 𝑑×𝑞 𝐿
.

19. Application to Circuit-SAT
problem

20. • DAG function 𝜇 𝐺: 𝑉𝐺 ↦ ℝ4
• 𝜇 𝐺 𝑣 = One−Hot 𝑡𝑦𝑝𝑒 𝑣
where 𝑡𝑦𝑝𝑒 v ∈ 𝐀𝐧𝐝, 𝐎𝐫, 𝐍𝐨𝐭, 𝐕𝐚𝐫𝐢𝐚𝐛𝐥𝐞
• Each node representing either a Boolean variable or a logical gate.
𝑥
1
2
3
0
0
0
1
0
0
1
0
1
0
0
0
Variables in sources Only one sink

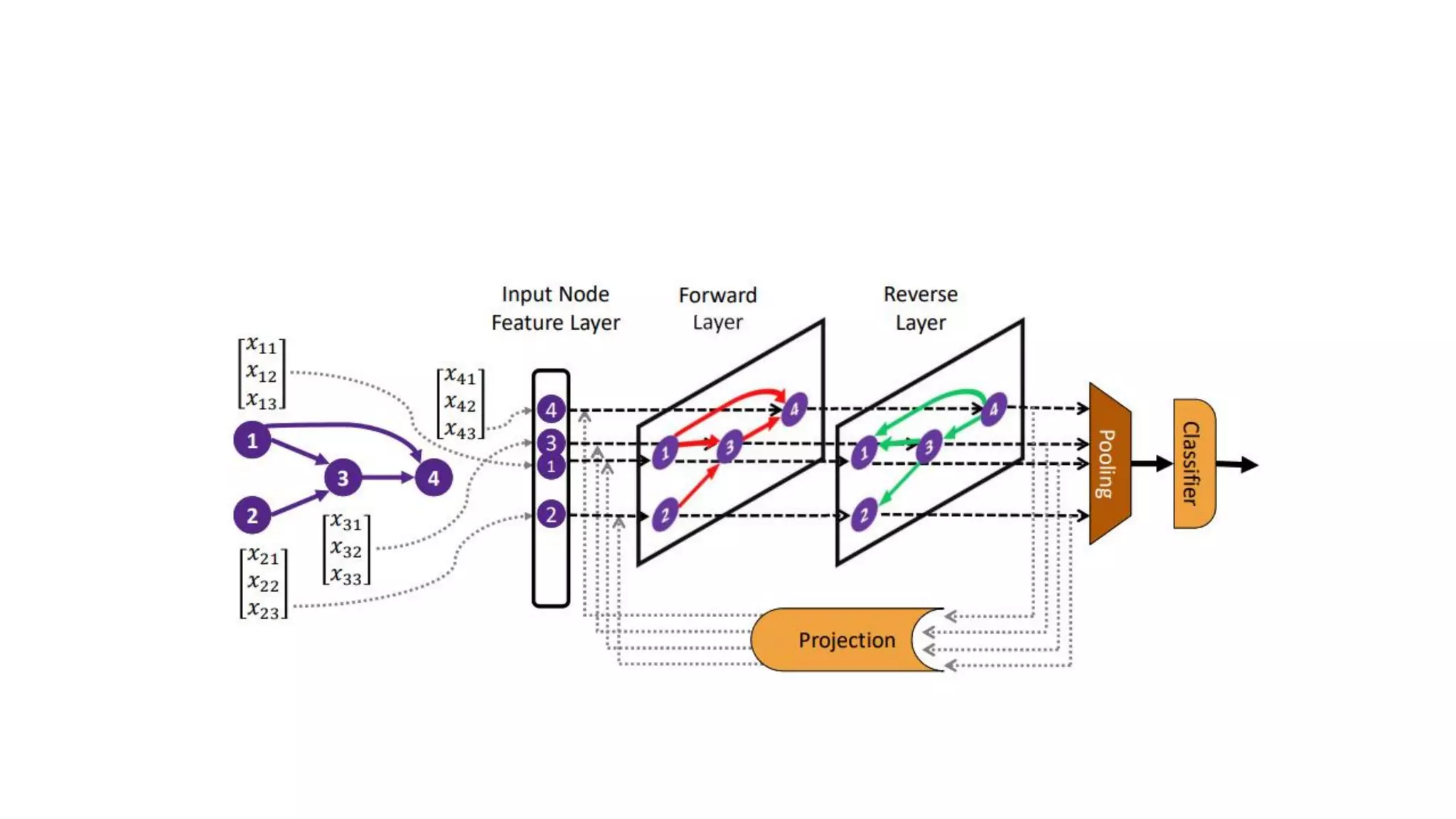
21. Solver Network
• Embedding function ℰℬ:
• multi-layer recursive embedding with interleaving forward and
reversed layers
• Last layer is a reversed layer so we can read the output from
Variable nodes.
• Output space encode the soft assignment (in range [0−1]) to the
corresponding variable node in the input circuit.
• ℱ 𝜃 acts as policy network.
Pooling: Retrieve only the sink nodes

22. Evaluator Network
• 𝑆 𝑚𝑎𝑥 𝑎1, 𝑎2, … , 𝑎 𝑛 =
σ 𝑖=1
𝑛
𝑎 𝑖 𝑒 Τ𝑎 𝑖 𝜏
σ𝑖=1
𝑛
𝑒 Τ𝑎 𝑖 𝜏 , 𝑆 𝑚𝑖𝑛 𝑎1, 𝑎2, … , 𝑎 𝑛 =
σ 𝑖=1
𝑛
𝑎 𝑖 𝑒 Τ−𝑎 𝑖 𝜏
σ𝑖=1
𝑛
𝑒− Τ𝑎 𝑖 𝜏
• For 𝜏 = +∞, 𝑆 𝑚𝑎𝑥() and 𝑆 𝑚𝑖𝑛() are arithmetic mean.
• E.g.
• 𝒂 = 1, 2, 3 , 𝜏 = +∞
• 𝑆 𝑚𝑎𝑥 𝒂 = 𝑆 𝑚𝑖𝑛 𝒂 =
1⋅𝑒0+2⋅𝑒0+3⋅𝑒0
𝑒0+𝑒0+𝑒0 =
1+2+3
3
= 2
• For 𝜏 → 0, 𝑆 𝑚𝑎𝑥 → max(), 𝑆 𝑚𝑖𝑛 → min()
• E.g.
• 𝒂 = 1, 2, 3 , 𝜏 = 0.01
• 𝑆 𝑚𝑎𝑥 𝒂 =
1⋅𝑒 Τ1 0.01+2⋅𝑒 Τ2 0.01+3⋅𝑒 Τ3 0.01
𝑒 Τ1 0.01+𝑒 Τ2 0.01+𝑒 Τ3 0.01 =
1𝑒100+2𝑒200+3𝑒300
𝑒100+𝑒200+𝑒300 ≈
3𝑒300
𝑒300 = 3
• 𝑆 𝑚𝑖𝑛 𝒂 =
1⋅𝑒 Τ−1 0.01+2⋅𝑒 Τ−2 0.01+3⋅𝑒 Τ−3 0.01
𝑒 Τ−1 0.01+𝑒 Τ−2 0.01+𝑒 Τ−3 0.01 =
1𝑒−100+2𝑒−200+3𝑒−300
𝑒−100+𝑒−200+𝑒−300 ≈
𝑒−100
𝑒−100 = 1

23. Evaluator Network (cont’d)
• For any given circuit 𝜇 𝐺, define the soft evaluation function ℛ 𝐺 as a
DAG that shares the same topology 𝐺 with the circuit 𝜇 𝐺.
• Except that replace each
• And node to smooth min (𝑆 𝑚𝑎𝑥)
• Or node to smooth max (𝑆 𝑚𝑖𝑛)
• Not nodes to 𝒩 𝑧 = 1 − 𝑧
• At a low enough temperature (𝜏), if for a given input assignment,
ℛ 𝐺 yields a value strictly greater than 0.5, then that assignment
can be seen as a satisfying solution for the circuit.
• ℛ 𝐺 acts as reward network.

24. Optimization
• 𝒮 𝜃: 𝒢 ↦ [0, 1] as 𝑆 𝜃 𝜇 𝐺 = ℛ 𝐺(ℱ 𝜃(𝜇 𝐺))
• Use the policy network to produce assignment and feed to reward
network to validate the satisfiability.
• Minimize the loss function
ℒ 𝑠 =
1−𝑠 𝜅
1−𝑠 𝜅+𝑠 𝜅 where 𝑠 = 𝒮 𝜃(𝜇 𝐺) and 𝜅 ≥ 1
• Could be seen as the portion of un-satisfiability.

25. Experimental evaluation

26. • Baseline: NeuroSAT
• Assume input problems come in CNF.
• Convert the input CNF into circuit before feeding to proposed
model (DG-DAGRNN).
• Use the same generation process in NeuroSAT to produce the
random dataset.
• 300K SAT and UNSAT pairs
• Number of Boolean variables: 3 to 10
• Performance metric: the percentage of SAT problems in the test
set that each model can actually find a SAT solution for.

27. number of recurrences 𝑇 (for embedding) increases
In-Sample test Out-of-Sample test (Use 3-10 variables during training)
number of variables in test set

28. Graph k-coloring
• Given an undirected graph 𝐺 with 𝑘 color values, in graph k-
coloring decision problem, seek to find a mapping from the graph
nodes to the color set such that no adjacent nodes in the graph
have the same color.
Source: https://en.wikipedia.org/wiki/Graph_coloring

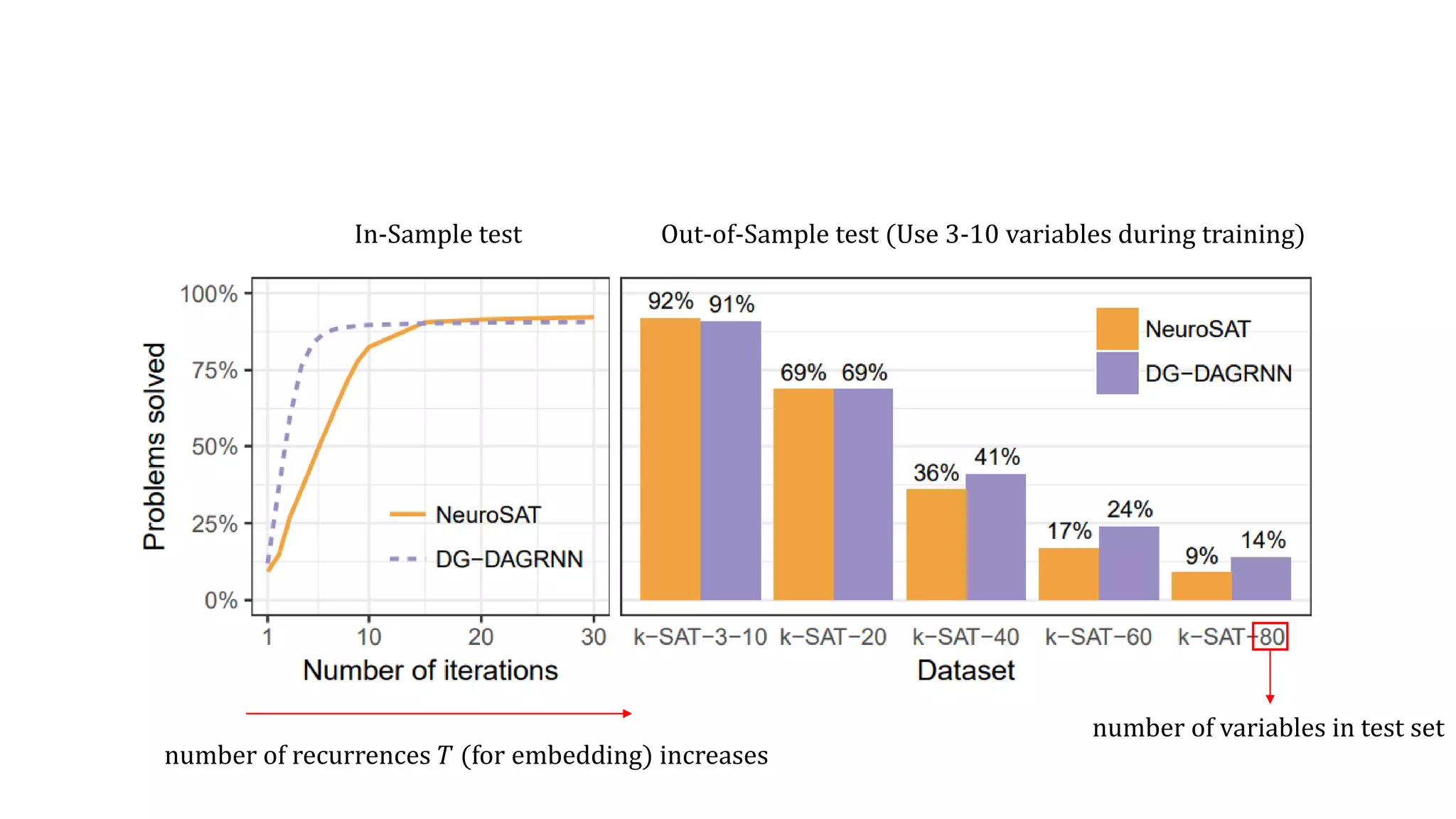
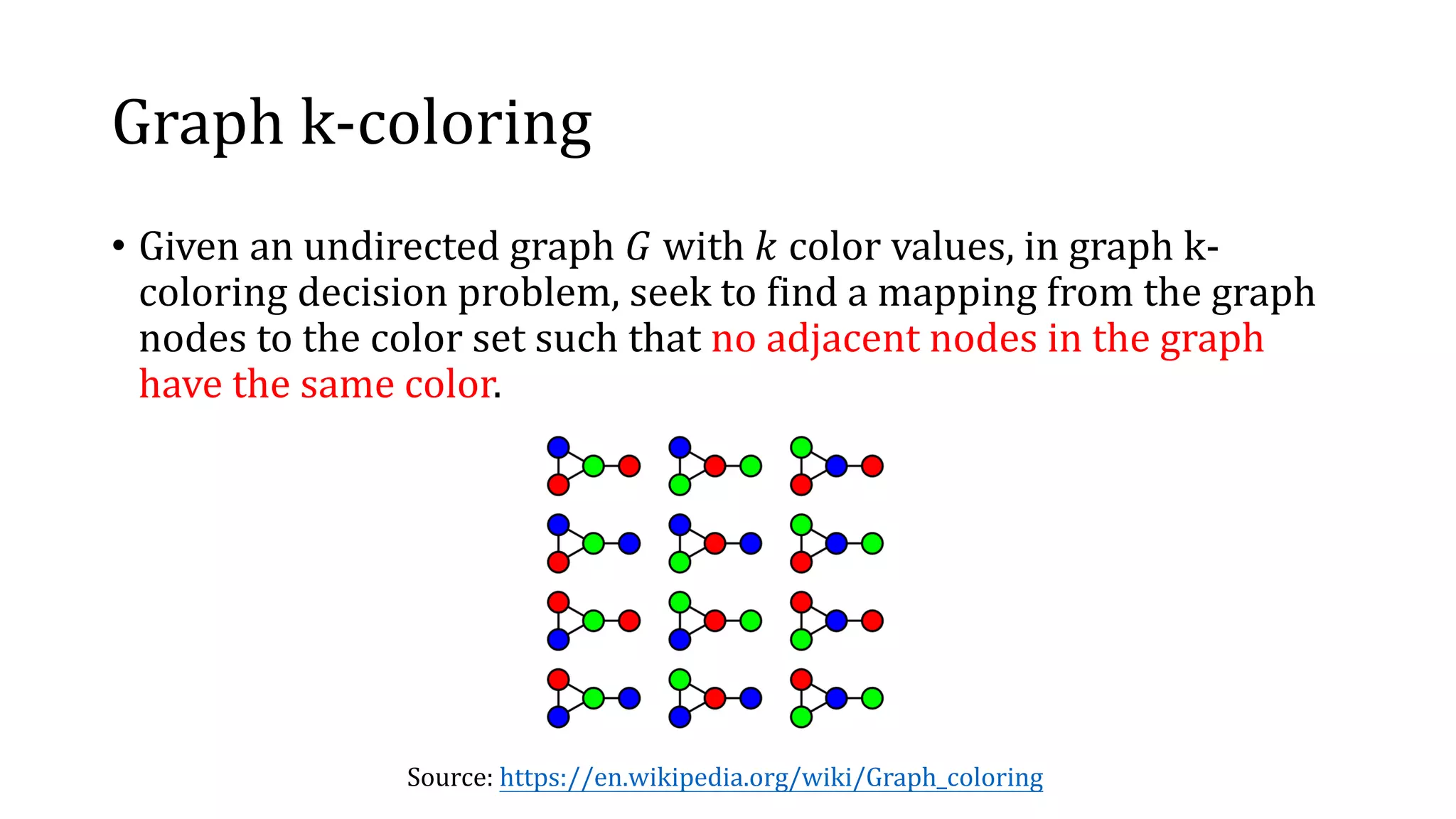
29. Graph k-coloring (cont’d)
• Given a graph with 𝑁 nodes and maximum 𝑘 allowed colors,
• Define 𝑥𝑖𝑗 for 1 ≤ 𝑖 ≤ 𝑁 and 1 ≤ 𝑗 ≤ 𝑘, where 𝑥𝑖𝑗 = 1 indicates
that the 𝑖th node is colored by the 𝑗th color.
• Transform the problem to SAT problem with Boolean CNF:
• ⋀𝑖=1
𝑁
(⋁𝑗=1
𝑘
𝑥𝑖𝑗) ∧ [⋀ 𝑝,𝑞 ∈𝐸(⋀𝑗=1
𝑘
(¬𝑥 𝑝𝑗 ∨ ¬𝑥 𝑞𝑗))]
• Left set of clauses (red): ensure that each node of the graph takes at least
one color.
• Right set of clauses (blue): constrain that the neighboring nodes cannot
take the same color. 𝒙 𝒑𝒋 𝒙 𝒒𝒋 (¬𝑥 𝑝𝑗 ∨ ¬𝑥 𝑞𝑗)
0 0 1
0 1 1
1 0 1
1 1 0

30. Example
blue green red
1 T F F
2 F F T
3 F T F
4 F F T
1
3
2
4
⋀𝑖=1
𝑁
(⋁𝑗=1
𝑘
𝑥𝑖𝑗) ∧ [⋀ 𝑝,𝑞 ∈𝐸(⋀𝑗=1
𝑘
(¬𝑥 𝑝𝑗 ∨ ¬𝑥 𝑞𝑗))]
colornode

31. • Dataset 1
• number of nodes: 6-10
• edge percentage: 37%
• Generate random graph from 6 different distributions and then pair with random k color in
the range of 2 ≤ 𝑘 ≤ 4.
• Dataset 2
• Generate random trees with the same node number in dataset 1.
• Add random edges to graph until it become UNSAT.
• Remove the last added edge to form SAT problem.
• Proposed model could solve 48% and 27% in Dataset 1 and Dataset 2, respectively.
• Surprisingly, NeuroSAT could not solve any problems, which does not consist to
original paper.
• NeuroSAT may be sensitive to the change of problem distribution.

32. Discussion
• Propose a neural framework for efficiently learning a Circuit-SAT
solver.
• Rely on DAG-embedding architecture and efficient training
procedure.
• Solve the SAT problem in a fewer number of iterations compared
to the baseline.