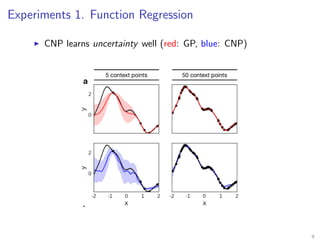
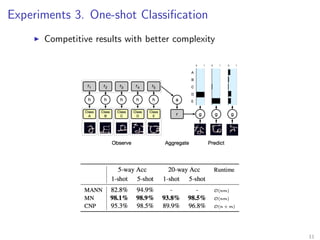
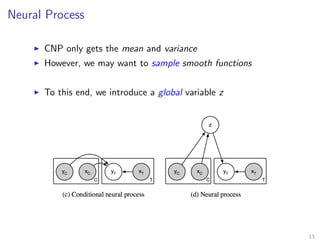
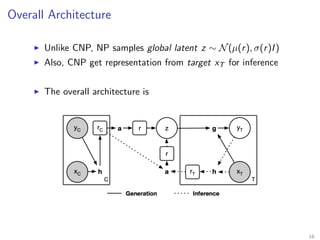
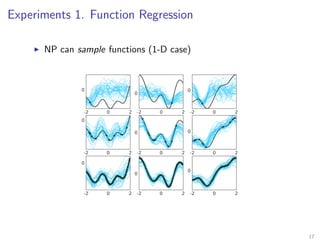
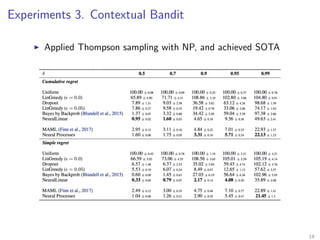
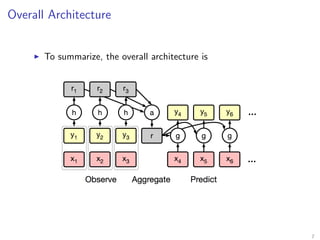
The document introduces Neural Processes (NP) and Conditional Neural Processes (CNP), which are models that aim to learn distributions of functions rather than single functions, improving upon traditional neural networks and Gaussian Processes. CNP focuses on predictive distributions given observations, while NP incorporates global latent variables for inference, allowing it to provide function samples and improve uncertainty estimates. The paper discusses architecture, complexity, training methods, and experiments demonstrating the efficacy of these models in tasks like regression and image completion.

1. Neural Processes
Sangwoo Mo
KAIST ALIN Lab.
August 28, 2018
1

2. Table of Contents
Overview
Conditional Neural Processes (ICML 2018)
Neural Processes (ICML Workshop 2018)
2

3. Table of Contents
Overview
Conditional Neural Processes (ICML 2018)
Neural Processes (ICML Workshop 2018)
3

4. Overview
Motivation: Can we learn a distribution of functions f ∼ P(f )
instead of a single function f with NN?
4

5. Overview
Motivation: Can we learn a distribution of functions f ∼ P(f )
instead of a single function f with NN?
Traditional NN: Dataset D is fixed, and infer with f
4

6. Overview
Motivation: Can we learn a distribution of functions f ∼ P(f )
instead of a single function f with NN?
Traditional NN: Dataset D is fixed, and infer with f
Neural Process: Given observation O, sample f ∼ P(f | O)
4

7. Overview
Motivation: Can we learn a distribution of functions f ∼ P(f )
instead of a single function f with NN?
Traditional NN: Dataset D is fixed, and infer with f
Neural Process: Given observation O, sample f ∼ P(f | O)
In modern language, NP does meta learning
4

8. Overview
Motivation: Can we learn a distribution of functions f ∼ P(f )
instead of a single function f with NN?
Traditional NN: Dataset D is fixed, and infer with f
Neural Process: Given observation O, sample f ∼ P(f | O)
We know GP is a good solution for this problem
4

9. Overview
Motivation: Can we learn a distribution of functions f ∼ P(f )
instead of a single function f with NN?
Traditional NN: Dataset D is fixed, and infer with f
Neural Process: Given observation O, sample f ∼ P(f | O)
We know GP is a good solution for this problem
However, GP suffers from high complexity O(n3)
4

10. Overview
Motivation: Can we learn a distribution of functions f ∼ P(f )
instead of a single function f with NN?
Traditional NN: Dataset D is fixed, and infer with f
Neural Process: Given observation O, sample f ∼ P(f | O)
We know GP is a good solution for this problem
However, GP suffers from high complexity O(n3)
NP combines both advantages of NN and GP
4

11. Table of Contents
Overview
Conditional Neural Processes (ICML 2018)
Neural Processes (ICML Workshop 2018)
5

12. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
6

13. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
6

14. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
To be clear, the model follows 4 steps
6

15. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
To be clear, the model follows 4 steps
1 ri = hθ(xi , yi ) ∀(xi , yi ) ∈ O
6

16. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
To be clear, the model follows 4 steps
1 ri = hθ(xi , yi ) ∀(xi , yi ) ∈ O
2 r = r1 ⊕ r2 · · · ⊕ rn
6

17. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
To be clear, the model follows 4 steps
1 ri = hθ(xi , yi ) ∀(xi , yi ) ∈ O
2 r = r1 ⊕ r2 · · · ⊕ rn
3 φi = gθ(xi , r) ∀(xi ) ∈ T
6

18. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
To be clear, the model follows 4 steps
1 ri = hθ(xi , yi ) ∀(xi , yi ) ∈ O
2 r = r1 ⊕ r2 · · · ⊕ rn
3 φi = gθ(xi , r) ∀(xi ) ∈ T
4 Qθ(f (T ) | O, T ) = xi ∈T Q(f (xi ) | φi )
6

19. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
To be clear, the model follows 4 steps
1 ri = hθ(xi , yi ) ∀(xi , yi ) ∈ O
2 r = r1 ⊕ r2 · · · ⊕ rn
3 φi = gθ(xi , r) ∀(xi ) ∈ T
4 Qθ(f (T ) | O, T ) = xi ∈T Q(f (xi ) | φi )
Step 2 and 4 enforce permutation invariance for O and T
6

20. Conditional Neural Process
Let O = {(xi , yi )} be observation and T = {xi } be target
We aim to learn a predictive distribution Qθ(f (T ) | O, T )
Idea: Learn encoder hθ(xi , yi ) and decoder gθ(xi , r)
To be clear, the model follows 4 steps
1 ri = hθ(xi , yi ) ∀(xi , yi ) ∈ O
2 r = r1 ⊕ r2 · · · ⊕ rn
3 φi = gθ(xi , r) ∀(xi ) ∈ T
4 Qθ(f (T ) | O, T ) = xi ∈T Q(f (xi ) | φi )
Step 2 and 4 enforce permutation invariance for O and T
The complexity is O(n) (much faster than GP!)
6

21. Overall Architecture
To summarize, the overall architecture is
7

22. Training CNP
For training, we randomly sample1 ON from O
1
The paper used ”first” N samples, but I guess it would be fine too
8

23. Training CNP
For training, we randomly sample1 ON from O
and minimize NLL for both observed and unobserved data
1
The paper used ”first” N samples, but I guess it would be fine too
8

24. Training CNP
For training, we randomly sample1 ON from O
and minimize NLL for both observed and unobserved data
Formally, let O = {(xi , yi )}n
i=1, then the loss is
1
The paper used ”first” N samples, but I guess it would be fine too
8

25. Training CNP
For training, we randomly sample1 ON from O
and minimize NLL for both observed and unobserved data
Formally, let O = {(xi , yi )}n
i=1, then the loss is
L(θ) = −Ef ∼P [EN [log Qθ(y1:n | ON, x1:n)]]
1
The paper used ”first” N samples, but I guess it would be fine too
8

26. Experiments 1. Function Regression
CNP learns uncertainty well (red: GP, blue: CNP)
9

27. Experiments 2. Image Completion
Complete image with few observed pixels
Uncertainty helps active learning (select high variance)
10

28. Experiments 3. One-shot Classification
Competitive results with better complexity
11

29. Table of Contents
Overview
Conditional Neural Processes (ICML 2018)
Neural Processes (ICML Workshop 2018)
12

30. Neural Process
CNP only gets the mean and variance
However, we may want to sample smooth functions
13

31. Neural Process
CNP only gets the mean and variance
However, we may want to sample smooth functions
To this end, we introduce a global variable z
13

32. NP Inference
Unlike CNP, NP inference is not trivial (due to latent z)
14

33. NP Inference
Unlike CNP, NP inference is not trivial (due to latent z)
The generative model of NP is
p(z, y1:n | x1:n) = p(z)
n
i=1
N(yi | g(xi , z), σ2
)
14

34. NP Inference
Unlike CNP, NP inference is not trivial (due to latent z)
The generative model of NP is
p(z, y1:n | x1:n) = p(z)
n
i=1
N(yi | g(xi , z), σ2
)
To estimate ELBO, take variational posterior q(z | x1:n, y1:n)
14

35. NP Inference
Unlike CNP, NP inference is not trivial (due to latent z)
The generative model of NP is
p(z, y1:n | x1:n) = p(z)
n
i=1
N(yi | g(xi , z), σ2
)
To estimate ELBO, take variational posterior q(z | x1:n, y1:n)
log p(y1:n | x1:n)
≥ Eq(z|x1:n,y1:n)
n
i=1
log p(yi | xi , z) + log
p(z)
q(z | x1:n, y1:n)
14

36. NP Inference
Let x1:m, y1:m be O and xm+1:n, ym+1:n be T
15

37. NP Inference
Let x1:m, y1:m be O and xm+1:n, ym+1:n be T
Now we maximize test time likelihood
log p(ym+1:n | x1:n, y1:m)
≥ Eq(z|x1:n,y1:n)
n
i=m+1
log p(yi | xi , z) + log
p(z | x1:m, y1:m)
q(z | x1:n, y1:n)
15

38. NP Inference
Let x1:m, y1:m be O and xm+1:n, ym+1:n be T
Now we maximize test time likelihood
log p(ym+1:n | x1:n, y1:m)
≥ Eq(z|x1:n,y1:n)
n
i=m+1
log p(yi | xi , z) + log
p(z | x1:m, y1:m)
q(z | x1:n, y1:n)
To estimate, also take variational posterior q(z | x1:m, y1:m)
15

39. Overall Architecture
Unlike CNP, NP samples global latent z ∼ N(µ(r), σ(r)I)
Also, CNP get representation from target xT for inference
The overall architecture is
16

40. Experiments 1. Function Regression
NP can sample functions (1-D case)
17

41. Experiments 2. Image Completion
NP can sample functions (2-D case)
18

42. Experiments 3. Contextual Bandit
Applied Thompson sampling with NP, and achieved SOTA
19

43. Summary
Introduced NP, combination of NN and GP
Introduced two variants: CNP and NP
CNP predicts uncertainty locally, and get mean & variance
NP predicts uncertainty globally, and get samples
Both has own advantages, and may can use on situation
20