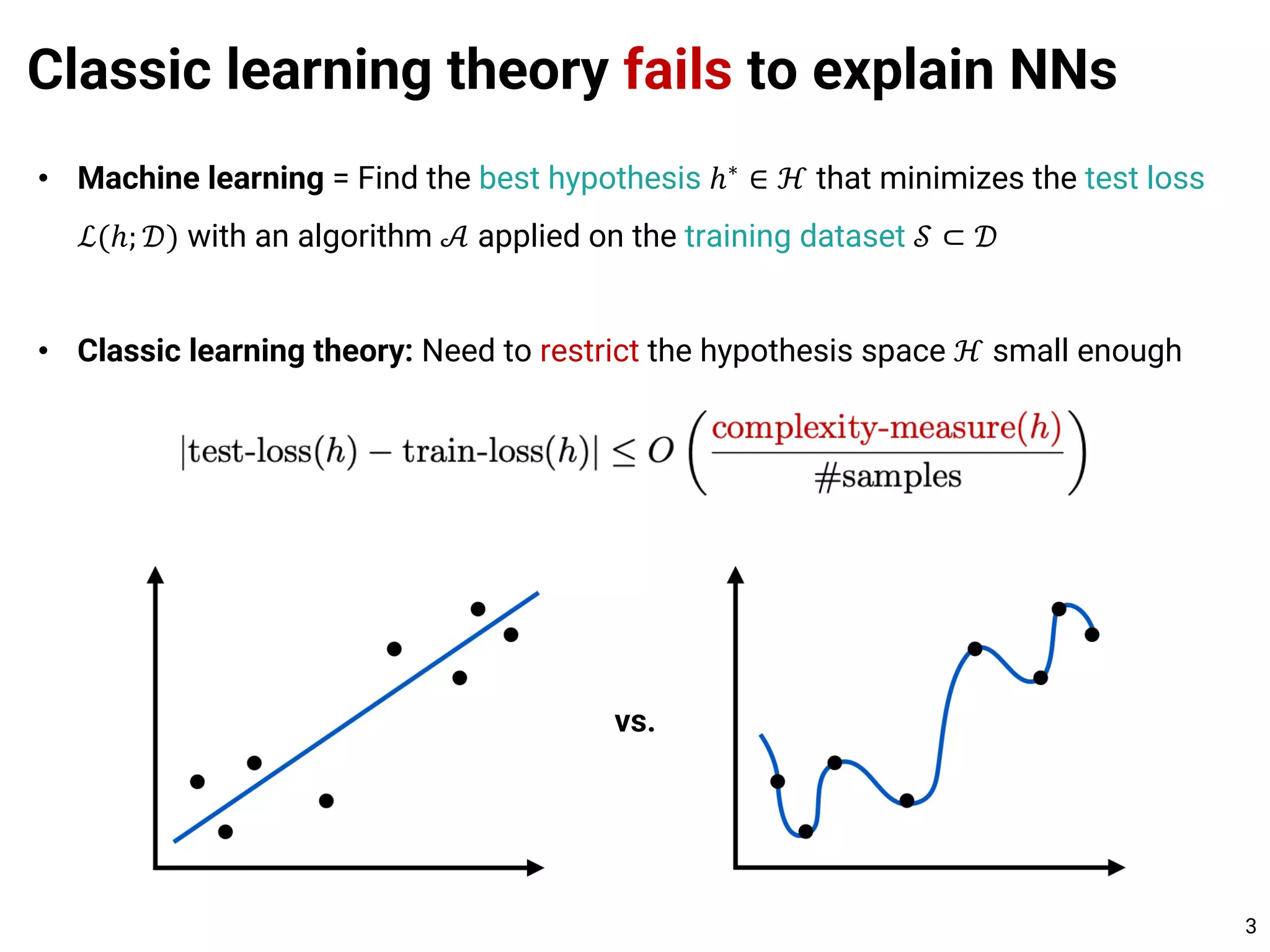
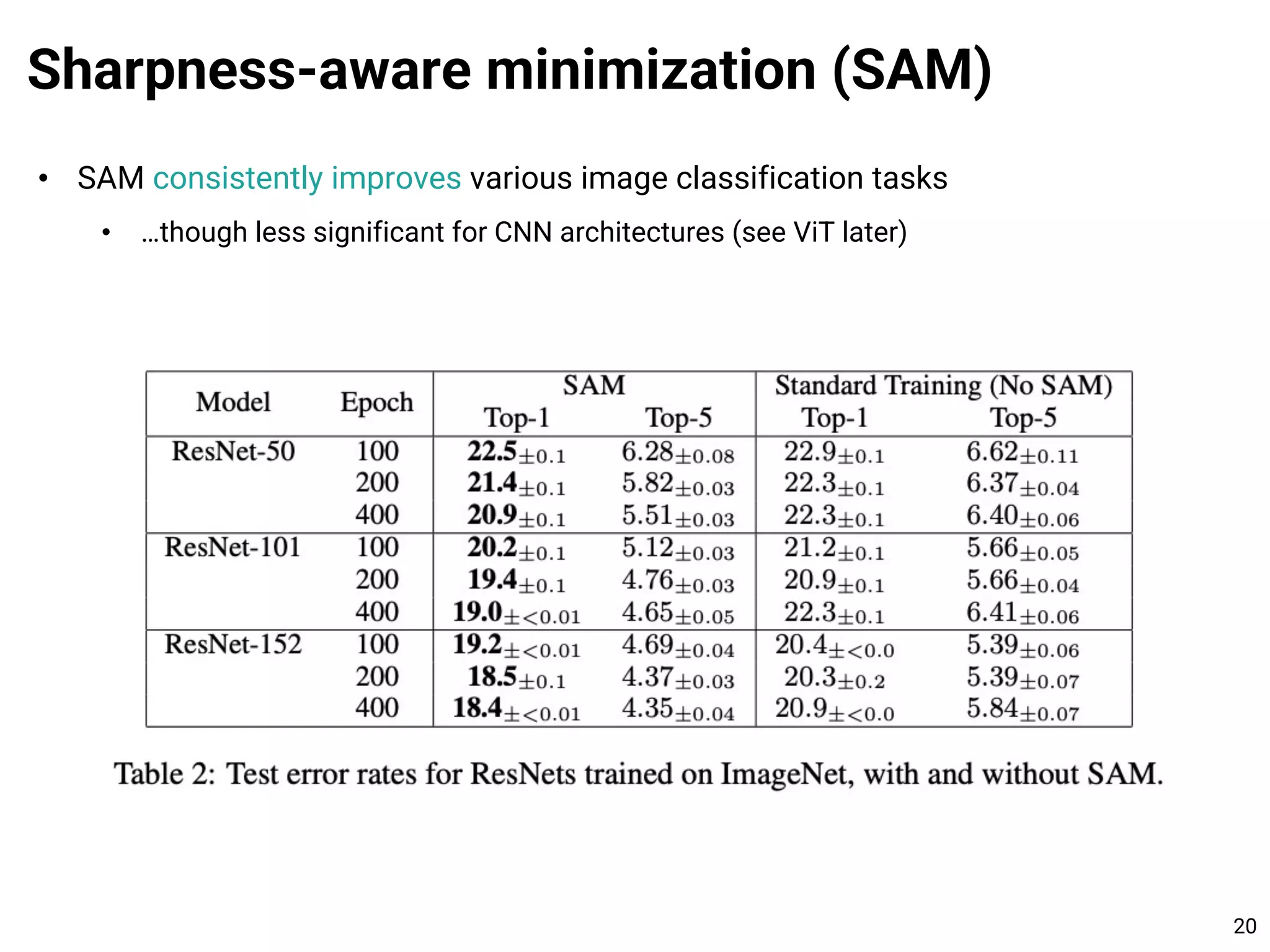
The document discusses recent theories on why deep neural networks generalize well despite being highly overparameterized. Classic learning theory, which assumes restricting the hypothesis space is necessary for generalization, fails to explain modern neural networks. Recent studies suggest neural networks generalize because 1) their complexity is underestimated and 2) SGD regularization finds flat minima. Sharpness-aware minimization (SAM) directly optimizes for flat minima and consistently improves generalization, especially for vision transformers which have sharper loss landscapes than ResNets. SAM produces more interpretable attention maps and significantly boosts performance of vision transformers and MLP-Mixers on in-domain and out-of-domain tasks.

1. Learning Theory 101
…and Towards Learning the Flat Minima
2021.07.12.
KAIST ALIN-LAB
Sangwoo Mo
1

2. Why deep learning works well?
2
1. Expressivity. Can NNs approximate any functions?
• Yes – universal approximation theorem
2. Optimization. Can we find the global minima of NNs?
• Yes – for overparametrized networks, all local minima ≈ global minima
• Note: zero training error does not imply zero test error
3. Generalization. Can NNs generalize for the unseen data?
• Old wisdom = No! – NNs would be overfitted (i.e., bias-variance trade-off)
• Recent studies:
• lots of efforts to explain the generalization of NNs
• some theories partly explain the phenomena

3. Classic learning theory fails to explain NNs
3
• Machine learning = Find the best hypothesis ℎ∗
∈ ℋ that minimizes the test loss
ℒ(ℎ; 𝒟) with an algorithm 𝒜 applied on the training dataset 𝒮 ⊂ 𝒟
• Classic learning theory: Need to restrict the hypothesis space ℋ small enough
vs.

4. Classic learning theory fails to explain NNs
4
• Machine learning = Find the best hypothesis ℎ∗
∈ ℋ that minimizes the test loss
ℒ(ℎ; 𝒟) with an algorithm 𝒜 applied on the training dataset 𝒮 ⊂ 𝒟
• Classic learning theory: Need to restrict the hypothesis space ℋ small enough
• Classic complexity measures
• ℋ for finite hypothesis space
• VC dimension (infinite hypothesis → finite complexity measure)
• # of parameters…
• ⇒ Not applicable for the modern deep networks!

5. Classic learning theory fails to explain NNs
5
• In reality…
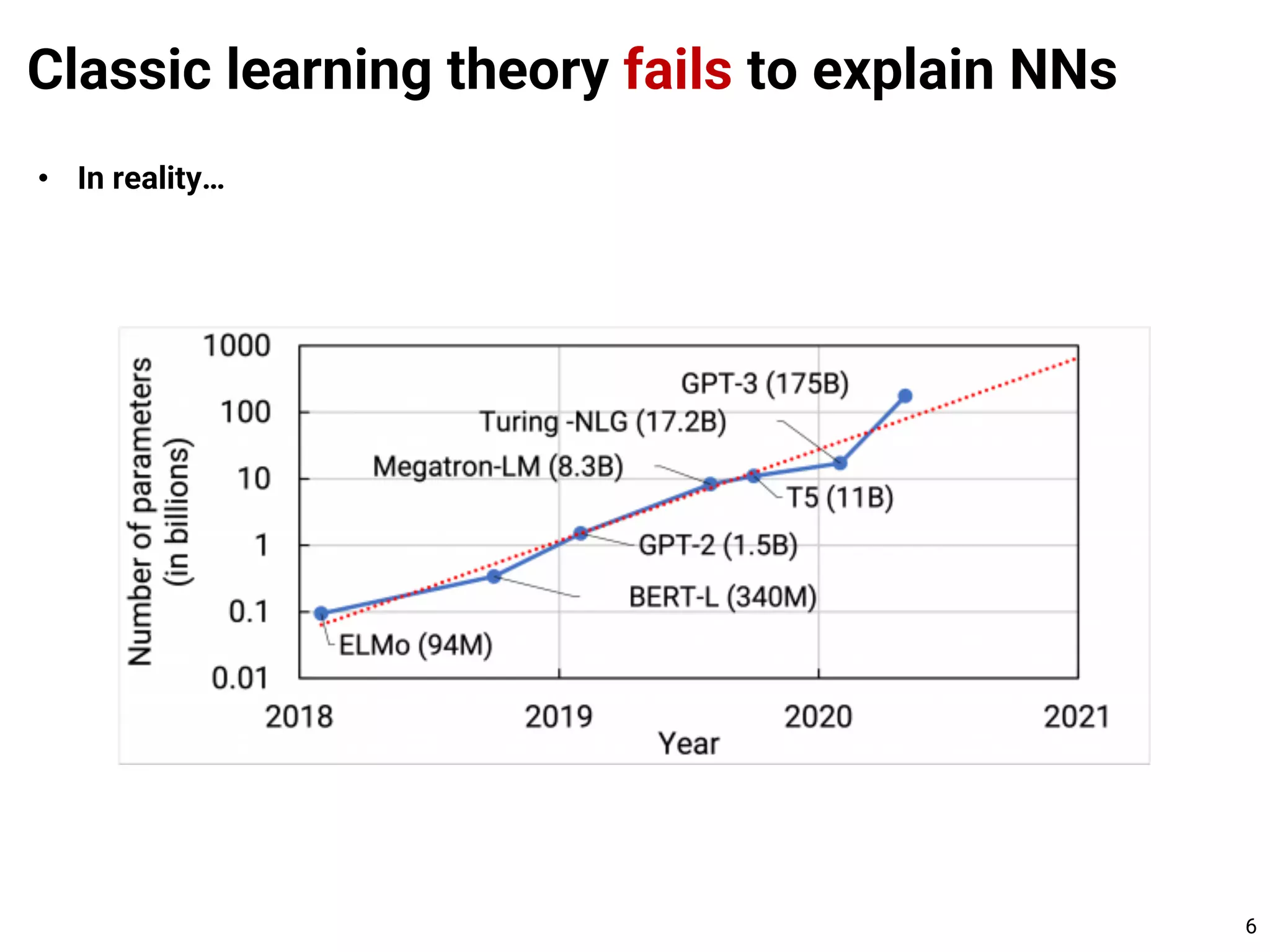
[1] Zhang et al. Understanding deep learning requires rethinking generalization. ICLR 2017.
[2] Nakkiran et al. Deep Double Descent: Where Bigger Models and More Data Hurt. ICLR 2020.

6. Classic learning theory fails to explain NNs
6
• In reality…

7. Classic learning theory fails to explain NNs
7
• In reality…

8. 1. The complexity measure 𝑚(ℎ) is not tight
• Compression approach
• There is a smaller model ℎ′ that is almost identical to the original model ℎ
• Then, we consider the tighter complexity measure 𝑚(ℎ!)
Why it happens?
8
[1] Arora et al. Stronger generalization bounds for deep nets via a compression approach. ICML 2018.
[2] Frankle et al. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. ICLR 2019.

9. 1. The complexity measure 𝑚(ℎ) is not tight
• Representation learning approach
• Upon the expressive representation, it suffices to consider the simple classifier
Why it happens?
9
[1] Bansal et al. For self-supervised learning, Rationality implies generalization, provably. ICLR 2021.

10. 2. The algorithm 𝒜 implicitly regularizes the search space .
ℋ ⊂ ℋ
• SGD finds simpler solution
• In overparameterization regime, there are infinitely many solutions
• SGD finds the model with smaller norm & sparser structure
• ⇒ Double descent (more overparameterization = better generalization)
Why it happens?
10
[1] Yun et al. A Unifying View on Implicit Bias in Training Linear Neural Networks. ICLR 2021.

11. 2. The algorithm 𝒜 implicitly regularizes the search space .
ℋ ⊂ ℋ
• SGD finds flat minima
• Perturbation of SGD → escape sharp minima
• Best empirical correlation between theory and practice
Why it happens?
11
[1] Jiang et al. Fantastic Generalization Measures and Where to Find Them. ICLR 2020.

12. • Optimal perturbation of SGD for flat minima
• Noise scale ∝ LR / batch size (need large LR or small batch size)
• Smaller noise scale (= larger batch size) for harder tasks
Flat minima
12
[1] Keskar et al. On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima. ICLR 2017.
[2] McCandlish et al. An Empirical Model of Large-Batch Training. arXiv 2018.

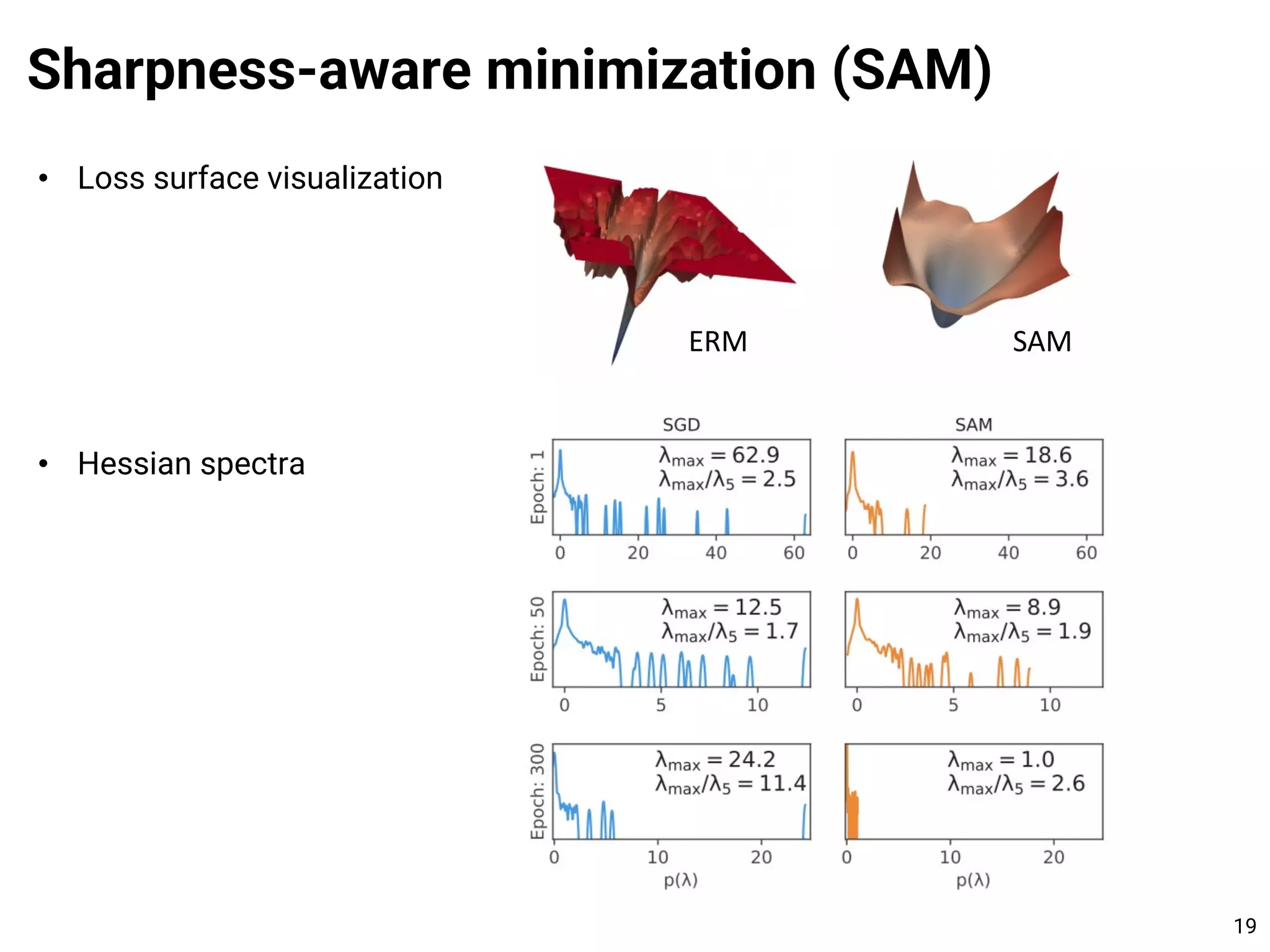
13. • Modern architectures + SGD = Flat minima
• e.g., skip connection, batch normalization
Flat minima
13
[1] Li et al. Visualizing the Loss Landscape of Neural Nets. NeurIPS 2018.
[2] Santurkar et al. How Does Batch Normalization Help Optimization? NeurIPS 2018.

14. • Modern architectures + SGD = Flat minima
• In fact, the minima are connected by some path
⇒ One can use them for fast ensemble
Flat minima
14
[1] Draxler et al. Essentially No Barriers in Neural Network Energy Landscape. ICML 2018.

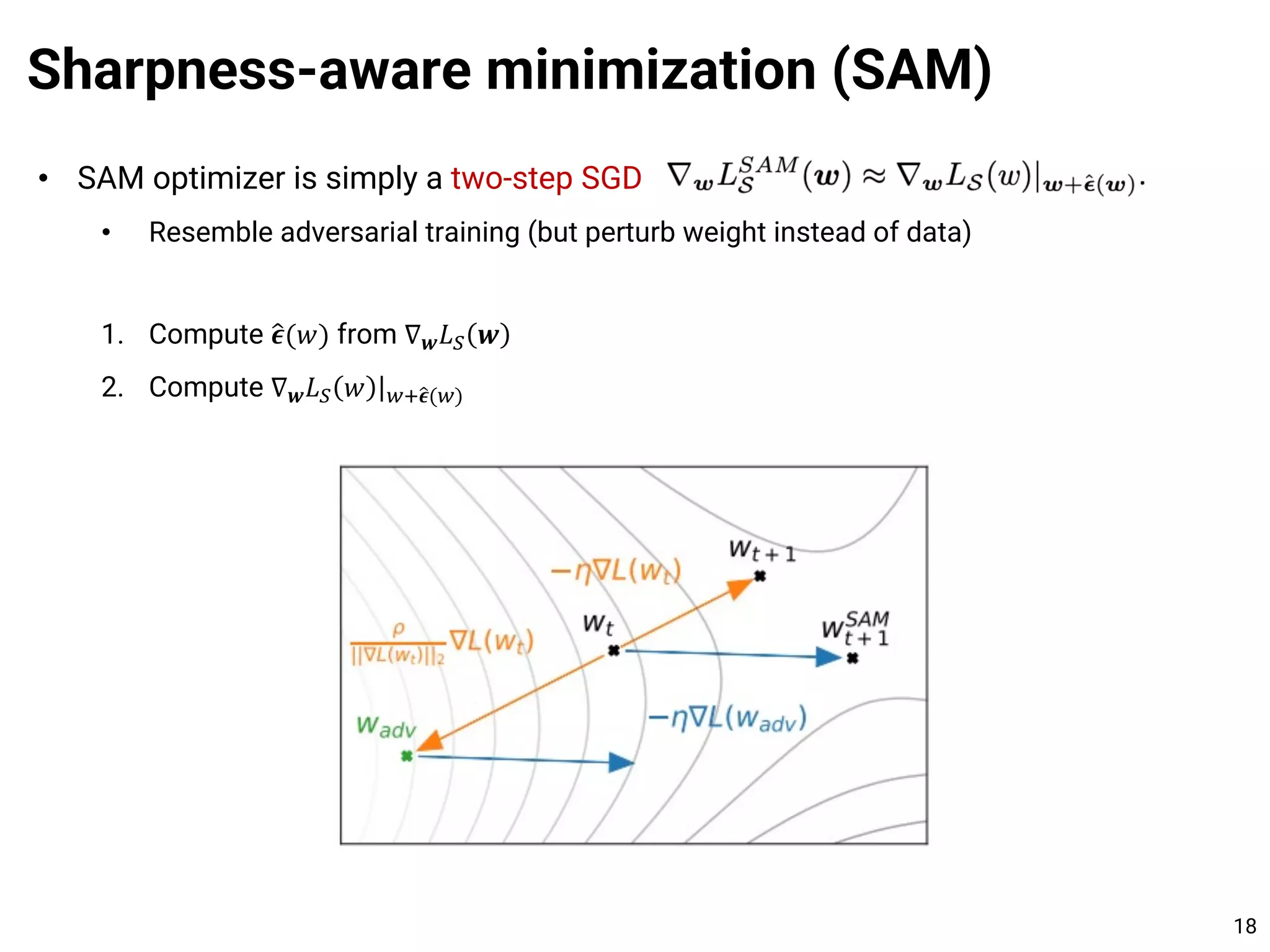
15. • Theorem. With high probability, the flatness-based bound says:
Sharpness-aware minimization (SAM)
15
[1] Foret et al. Sharpness-Aware Minimization for Efficiently Improving Generalization. ICLR 2021.

16. • Theorem. With high probability, the flatness-based bound says:
• SAM minimizes the minimax objective
• With 1st order Taylor approximation,
Sharpness-aware minimization (SAM)
16
[1] Foret et al. Sharpness-Aware Minimization for Efficiently Improving Generalization. ICLR 2021.

17. • Theorem. With high probability, the flatness-based bound says:
• SAM minimizes the minimax objective
• With 1st order Taylor approximation,
• By substituting ̂
𝜖(𝒘), the gradient estimator of SAM is
or simply,
Sharpness-aware minimization (SAM)
17
2nd order term is not necessary in practice
[1] Foret et al. Sharpness-Aware Minimization for Efficiently Improving Generalization. ICLR 2021.

18. • SAM optimizer is simply a two-step SGD
• Resemble adversarial training (but perturb weight instead of data)
1. Compute .
𝝐(𝑤) from ∇𝒘𝐿# 𝒘
2. Compute ∇𝒘𝐿# 𝑤 |$%&
𝝐($)
Sharpness-aware minimization (SAM)
18

19. • Loss surface visualization
• Hessian spectra
Sharpness-aware minimization (SAM)
19
ERM SAM

20. • SAM consistently improves various image classification tasks
• …though less significant for CNN architectures (see ViT later)
Sharpness-aware minimization (SAM)
20

21. • Vision Transformer (ViT): Transformer-only architecture using image patches
• MLP-Mixer: Replace Transformer with MLP layers
SAM + ViT/MLP-Mixer
21
[1] An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale. ICLR 2021.
[2] MLP-Mixer: An all-MLP Architecture for Vision. Under review.
MLP-Mixer: patch-wise MLP + channel-wise MLP

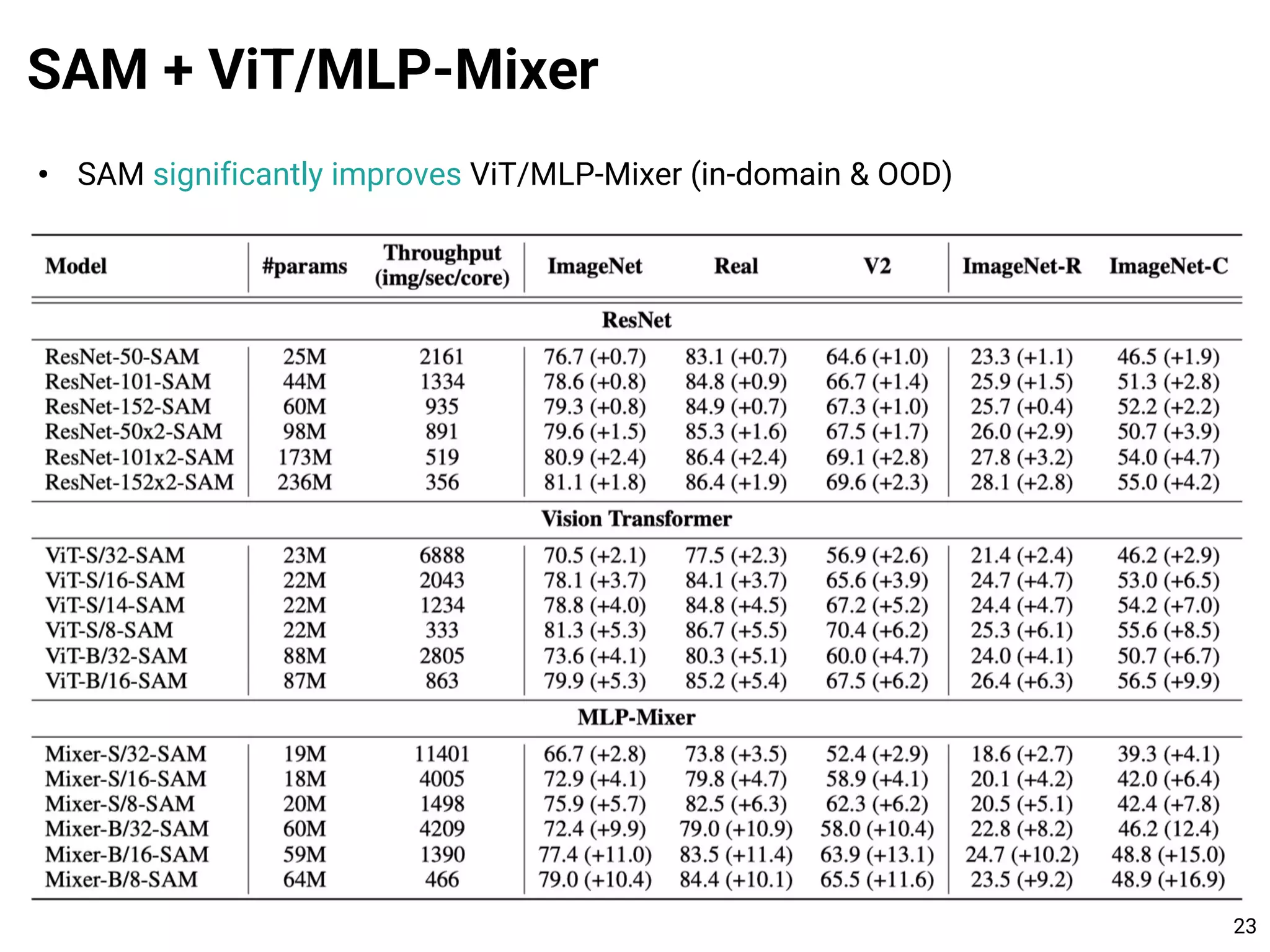
22. • Loss surface of ViT/MLP-Mixer are sharper than ResNet
• ViT/MLP-Mixer + SAM finds the flat minima ⇒ Outperforms ResNet
SAM + ViT/MLP-Mixer
22
[1] Chen et al. When Vision Transformers Outperform ResNets without Pretraining or Strong Data Augmentations. arXiv 2021.

23. • SAM significantly improves ViT/MLP-Mixer (in-domain & OOD)
SAM + ViT/MLP-Mixer
23

24. • ViT+SAM produces more interpretable attention maps
SAM + ViT/MLP-Mixer
24

25. • Deep learning requires rethinking generalization
• Flat minima could be a possible answer for the modern learning theory
• Sharpness-aware minimization (SAM) directly optimizes the flat minima
…and empirically performs well! (w/ nice properties for ViT)
Take-home message
25
Thank you for listening! 😀