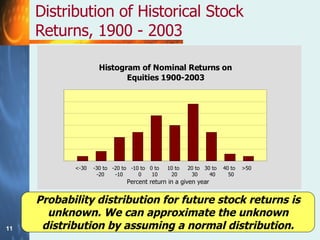
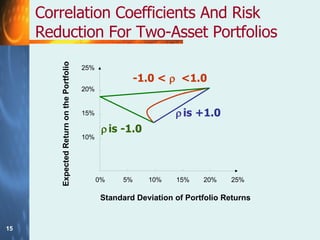
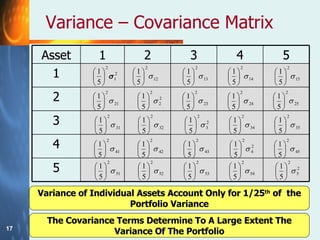
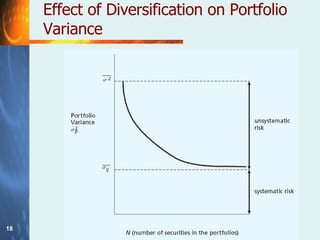
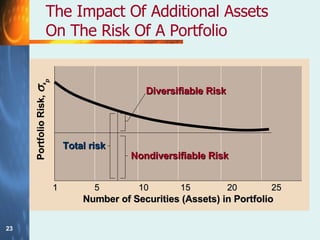
The document discusses the relationship between risk and return when investing. It states that there is a trade-off between expected risk and expected return, with higher risk investments typically offering higher returns to compensate investors for taking on more risk. It also discusses how diversification across multiple assets can reduce the non-systematic/diversifiable risk in a portfolio, but not the systematic/market risk that is related to movements in the overall market. The document defines beta as a measure of a stock's systematic risk relative to the market.

1. Chapter 5 The Trade-off between Risk and Return © 2007 Thomson South-Western

2. Introduction to Risk and Return Valuing risky assets - a task fundamental to financial management The three-step procedure is called discounted cash flow (DCF) analysis. Three-step procedure for valuing a risky asset 1. Determine the asset’s expected cash flows 2. Choose discount rate that reflects asset’s risk 3. Calculate present value (PV cash inflows - PV outflows)

3. Historical vs. Expected Returns Decisions Must Be Based On Expected Returns There Are Many Ways to Estimate Expected Returns Assume That Expected Return Going Forward Equals the Average Return in the Past Simple Way to Estimate Expected Return

4. Risk and Return Fundamentals Equity risk premium: the difference in equity returns and returns on safe investments implies that stocks are riskier than bonds or bills trade-off always arises between expected risk and expected return

5. Risk Aversion Risk Neutral Investors Seek the Highest Return Without Regard to Risk Risk Seeking Investors Have a Taste for Risk and Will Take Risk Even If They Cannot Expect a Reward for Doing So Risk Averse Investors Do Not Like Risk and Must Be Compensated For Taking It Historical Returns on Financial Assets Are Consistent with a Population of Risk-Averse Investors

6. Probability Distribution Probability distribution tells us what outcomes are possible and associates a probability with each outcome. Normal distribution

7. Two Assets With Same Expected Return But Different Distributions

8. Return on an Asset Return - The Total Gain or Loss Experienced on an Investment Over a Given Period of Time. An example.... Investor Bought Utilyco for $60/share Dividend = $6/share Sold for $66/share

9. Arithmetic Versus Geometric Returns Arithmetic return the simple average of annual returns: best estimate of expected return each year. Geometric average return the compound annual return to an investor who bought and held a stock t years: Geometric avg return= (1+R 1 )(1+R 2 )(1+R 3 )….(1+R t )] 1/t – 1 The Difference Between Arithmetic Returns and Geometric Returns Gets Bigger the More Volatile the Returns Are

10. Arithmetic Versus Geometric Returns The Difference Between Arithmetic Returns and Geometric Returns Gets Bigger the More Volatile the Returns Are AAR = 6.25% GAR = 5.78% An example.... Year Return -10% +12% +15% + 8%

11. Distribution of Historical Stock Returns, 1900 - 2003 Percent return in a given year Probability distribution for future stock returns is unknown. We can approximate the unknown distribution by assuming a normal distribution. <-30 -30 to -20 to -10 to 0 to 10 to 20 to 30 to 40 to >50 -20 -10 0 10 20 30 40 50

12. Variance A reasonable way to define risk is to focus on the dispersion of returns most common measure of dispersion used as a proxy for risk in finance is variance, or its square root, the standard deviation. distribution’s variance equals the expected value of squared deviations from the mean.

13. Expected Return For A Portfolio Most Investors Hold Multiple Asset Portfolios Key Insight of Portfolio Theory : Asset Return Adds Linearly, But Risk Is (Almost Always) Reduced in a Portfolio

14. Two-Asset Portfolio Standard Deviation Correlation Between Stocks Influences Portfolio Volatility

15. Correlation Coefficients And Risk Reduction For Two-Asset Portfolios 10% 15% 20% 25% 0% 5% 10% 15% 20% 25% Standard Deviation of Portfolio Returns Expected Return on the Portfolio  is +1.0 -1.0 <  <1.0  is -1.0

16. Portfolios of More Than Two Assets Five-Asset Portfolio Expected Return of Portfolio Is Still The Average Of Expected Returns Of The Two Stocks How Is The Variance of Portfolio Influenced By Number Of Assets in Portfolio?

17. Variance – Covariance Matrix 5 4 3 2 1 5 4 3 2 1 Asset The Covariance Terms Determine To A Large Extent The Variance Of The Portfolio 5 4 3 2 1 5 4 3 2 1 Asset 5 4 3 2 1 5 4 3 2 1 Asset Variance of Individual Assets Account Only for 1/25 th of the Portfolio Variance

18. Effect of Diversification on Portfolio Variance

19. Portfolio Risk variance cannot fall below the average covariance of securities in the portfolio Undiversifiable risk (systematic risk, market risk) Only systematic risk is priced in the market. Beta is one way to measure the systematic risk of an asset. Diversifiable risk (unsystematic risk, idiosyncratic risk, or unique risk)

20. What Is a Stock’s Beta? Beta Is a Measure of Systematic Risk What If Beta > 1 or Beta <1? The Stock Moves More Than 1% on Average When the Market Moves 1% (Beta > 1) The Stock Moves Less Than 1% on Average When the Market Moves 1% (Beta < 1) What If Beta = 1? The Stock Moves 1% on Average When the Market Moves 1% An “Average” Level of Risk

21. Diversifiable And Non-Diversifiable Risk As Number of Assets Increases, Diversification Reduces the Importance of a Stock’s Own Variance Diversifiable risk, unsystematic risk Only an Asset’s Covariance With All Other Assets Contributes Measurably to Overall Portfolio Return Variance Non-diversifiable risk, systematic risk

22. How Risky Is an Individual Asset? First Approach – Asset’s Variance or Standard Deviation What Really Matters Is Systematic Risk….How an Asset Covaries With Everything Else Use Asset’s Beta

23. The Impact Of Additional Assets On The Risk Of A Portfolio Number of Securities (Assets) in Portfolio Portfolio Risk,  k p Nondiversifiable Risk Diversifiable Risk Total risk 1 5 10 15 20 25