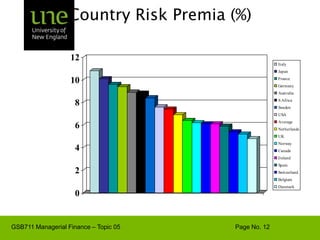
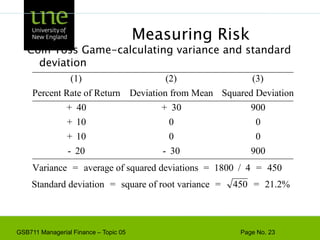
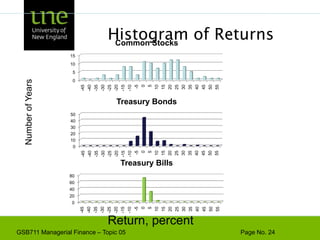
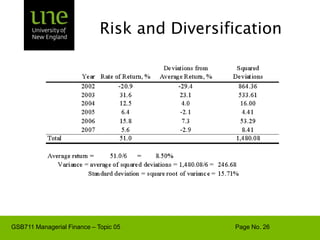
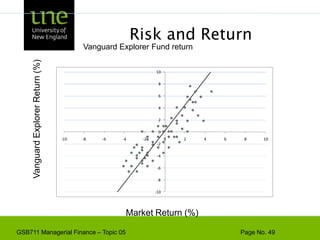
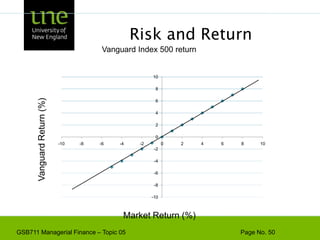
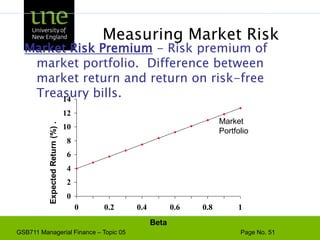
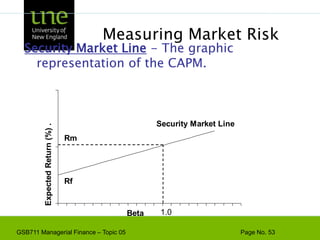
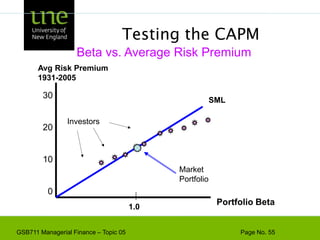
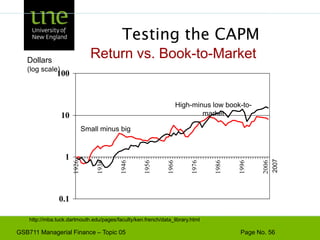
The document covers concepts of risk, return, and the Capital Asset Pricing Model (CAPM) as part of the Managerial Finance curriculum. It discusses various topics including rates of return, risk measurement, diversification, portfolio construction, and project risk in capital budgeting. Additionally, it highlights the impact of systematic and unsystematic risks on investment decisions and explores the relationship between risk and expected returns using beta as a key metric.

1. Risk, Return and Capital Asset Pricing ModelTopic 05GSB711 – Managerial FinanceReadings: Chapter: Introduction to Risk, Return and the Opportunity Cost of Capital (Pages 220 – 246) Questions: 1, 3, 6, 7 and Problems: 9, 13, 16, 20, 21 and 23.Chapter: Risk, Return and Capital Budgeting (Pages 248 – 273)Questions: 1, 2, 4 and Problems: 6, 7, 9, 10, 13, 16, 17, 21, 25 and 29.

2. Topics CoveredRates of Return: A ReviewA Century of Capital Market HistoryMeasuring RiskRisk & DiversificationMeasuring Market RiskBetaRisk and ReturnCAPMCapital Budgeting and Project Risk

3. Rates of Return

4. Rates of Return

5. Rates of Return

6. Nominal vs. RealRates of Return

7. Dow Jones Industrial Average (The Dow)Value of a portfolio holding one share in each of 30 large industrial firms.Standard & Poor’s Composite Index (The S&P 500)Value of a portfolio holding shares in 500 firms. Holdings are proportional to the number of shares in the issues.Market Indexes

8. The Value of an Investment of $1 in 1900$22,745Index$192$692008Source: Ibbotson AssociatesYear Start

9. Rates of ReturnCommon Stocks (1900-2007)2007

10. Expected Return

11. What is Risk?Risk, in traditional terms, is viewed as a ‘negative’. Webster’s dictionary, for instance, defines risk as “exposing to danger or hazard”. The Chinese symbols for risk, reproduced below, give a much better description of riskThe first symbol is the symbol for “danger”, while the second is the symbol for “opportunity”, making risk a mix of danger and opportunity.

12. Country Risk Premia (%)

13. Measuring RiskVariance - Average value of squared deviations from mean. A measure of volatility.Standard Deviation - Average value of squared deviations from mean. A measure of volatility.

14. Expected ReturnsExpected returns are based on the probabilities of possible outcomesIn this context, “expected” means average if the process is repeated many timesThe “expected” return does not even have to be a possible return

15. Example: Expected ReturnsSuppose you have predicted the following returns for stocks C and T in three possible states of nature. What are the expected returns?State Probability C TBoom 0.3 15 25Normal 0.5 10 20Recession ??? 2 1RC = .3(15) + .5(10) + .2(2) = 9.99%RT = .3(25) + .5(20) + .2(1) = 17.7%

16. Variance and Standard DeviationVariance and standard deviation still measure the volatility of returnsUsing unequal probabilities for the entire range of possibilitiesWeighted average of squared deviations

17. Example: Variance and Standard DeviationConsider the previous example. What are the variance and standard deviation for each stock?Stock C2 = .3(15-9.9)2 + .5(10-9.9)2 + .2(2-9.9)2 = 20.29 = 4.5Stock T2 = .3(25-17.7)2 + .5(20-17.7)2 + .2(1-17.7)2 = 74.41 = 8.63

18. PortfoliosA portfolio is a collection of assetsAn asset’s risk and return are important in how they affect the risk and return of the portfolioThe risk-return trade-off for a portfolio is measured by the portfolio expected return and standard deviation, just as with individual assets

19. Example: Portfolio WeightsSuppose you have $15,000 to invest and you have purchased securities in the following amounts. What are your portfolio weights in each security?$2000 of DCLK$3000 of KO$4000 of INTC$6000 of KEIDCLK: 2/15 = .133

20. KO: 3/15 = .2

21. INTC: 4/15 = .267

22. KEI: 6/15 = .4Portfolio Expected ReturnsThe expected return of a portfolio is the weighted average of the expected returns for each asset in the portfolioYou can also find the expected return by finding the portfolio return in each possible state and computing the expected value as we did with individual securities

23. Example: Expected Portfolio ReturnsConsider the portfolio weights computed previously. If the individual stocks have the following expected returns, what is the expected return for the portfolio?DCLK: 19.69%KO: 5.25%INTC: 16.65%KEI: 18.24%E(RP) = .133(19.69) + .2(5.25) + .167(16.65) + .4(18.24) = 13.75%

24. Portfolio VarianceCompute the portfolio return for each state:RP = w1R1 + w2R2 + … + wmRmCompute the expected portfolio return using the same formula as for an individual assetCompute the portfolio variance and standard deviation using the same formulas as for an individual asset

25. Coin Toss Game-calculating variance and standard deviationMeasuring Risk

26. Histogram of ReturnsNumber of YearsReturn, percent

27. Risk and DiversificationDiversification - Strategy designed to reduce risk by spreading the portfolio across many investments.Unique Risk - Risk factors affecting only that firm. Also called “diversifiable risk.”Market Risk - Economy-wide sources of risk that affect the overall stock market. Also called “systematic risk.”

28. Risk and Diversification

29. Risk and Diversification

30. DiversificationPortfolio diversification is the investment in several different asset classes or sectorsDiversification is not just holding a lot of assetsFor example, if you own 50 internet stocks, you are not diversifiedHowever, if you own 50 stocks that span 20 different industries, then you are diversified

31. 29Portfolio diversification with additional stocks in a portfolio

32. The Principle of DiversificationDiversification can substantially reduce the variability of returns without an equivalent reduction in expected returnsThis reduction in risk arises because worse than expected returns from one asset are offset by better than expected returns from anotherHowever, there is a minimum level of risk that cannot be diversified away and that is the systematic portion

33. Portfolio diversification and numbers of stocks in a portfolio

34. Diversifiable RiskThe risk that can be eliminated by combining assets into a portfolioOften considered the same as unsystematic, unique or asset-specific riskIf we hold only one asset, or assets in the same industry, then we are exposing ourselves to risk that we could diversify away

35. Total RiskTotal risk = systematic risk + unsystematic riskThe standard deviation of returns is a measure of total riskFor well-diversified portfolios, unsystematic risk is very smallConsequently, the total risk for a diversified portfolio is essentially equivalent to the systematic risk

36. Systematic Risk PrincipleThere is a reward for bearing riskThere is not a reward for bearing risk unnecessarilyThe expected return on a risky asset depends only on that asset’s systematic risk since unsystematic risk can be diversified away

37. Measuring Systematic RiskHow do we measure systematic risk?We use the beta coefficient to measure systematic riskWhat does beta tell us?A beta of 1 implies the asset has the same systematic risk as the overall marketA beta < 1 implies the asset has less systematic risk than the overall marketA beta > 1 implies the asset has more systematic risk than the overall market

38. Total versus Systematic RiskConsider the following information: Standard Deviation BetaSecurity C 20% 1.25Security K 30% 0.95Which security has more total risk?Which security has more systematic risk?Which security should have the higher expected return?

39. Beta and the Risk PremiumRemember that the risk premium = expected return – risk-free rateThe higher the beta, the greater the risk premium should beCan we define the relationship between the risk premium and beta so that we can estimate the expected return?YES!

40. Stock Market Volatility 1900-2007Std Dev2007

41. The Value of InvestmentsValue (August 2004 = 100)

42. Risk and Diversification

43. Risk and Diversification

44. Measuring Market RiskMarket Portfolio - Portfolio of all assets in the economy. In practice a broad stock market index is used to represent the market.Beta - Sensitivity of a stock’s return to the return on the market portfolio.

45. Measuring Market RiskExample - Turbo Charged Seafood has the following % returns on its stock, relative to the listed changes in the % return on the market portfolio. The beta of Turbo Charged Seafood can be derived from this information.

46. Example - continuedMeasuring Market Risk

47. Measuring Market RiskExample - continuedWhen the market was up 1%, Turbo average % change was +0.8%When the market was down 1%, Turbo average % change was -0.8% The average change of 1.6 % (-0.8 to 0.8) divided by the 2% (-1.0 to 1.0) change in the market produces a beta of 0.8.

48. Example - continuedMeasuring Market Risk

49. Portfolio BetasDiversification decreases variability from unique risk, but not from market risk.The beta of your portfolio will be an average of the betas of the securities in the portfolio.If you owned all of the S&P Composite Index stocks, you would have an average beta of 1.0

50. Betas calculated with price data from January 2003 thru December 2007Stock Betas

51. Risk and ReturnVanguard Explorer Fund returnVanguard Explorer Return (%)Market Return (%)

52. Risk and ReturnVanguard Index 500 returnVanguard Return (%)Market Return (%)

53. Measuring Market RiskMarket PortfolioMarket Risk Premium - Risk premium of market portfolio. Difference between market return and return on risk-free Treasury bills.

54. CAPM - Theory of the relationship between risk and return which states that the expected risk premium on any security equals its beta times the market risk premium.Measuring Market Risk

55. Measuring Market Risk1.0Security Market Line - The graphic representation of the CAPM.

56. Capital Asset Pricing Model R = rf + B ( rm - rf )CAPM

57. Testing the CAPMBeta vs. Average Risk PremiumAvg Risk Premium 1931-20053020100SMLInvestorsMarket PortfolioPortfolio Beta1.0

58. Testing the CAPMReturn vs. Book-to-MarketDollars(log scale)High-minus low book-to-marketSmall minus big2007http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html

59. Stock Expected Returns

60. Capital Budgeting & Project RiskWe discuss more on capital budgeting in a later topicThe project cost of capital depends on the use to which the capital is being put. Therefore, it depends on the risk of the project and not the risk of the company.

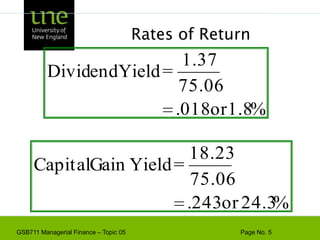
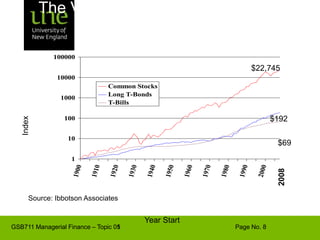
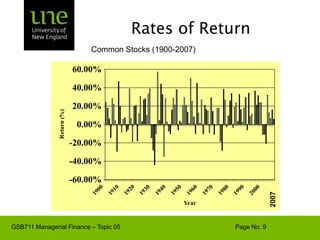
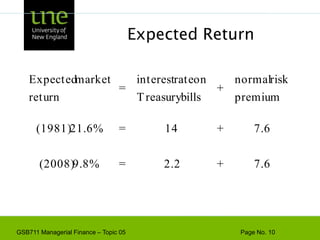
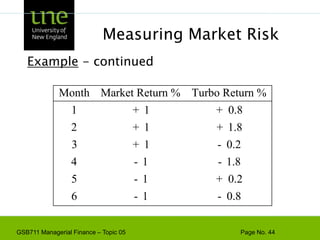
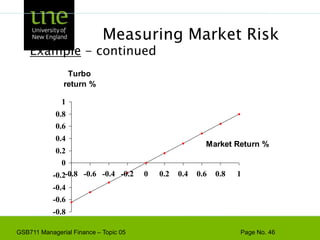
61. Capital Budgeting & ProjectExample - Based on the CAPM, ABC Company has a cost of capital of 17%. [4 + 1.3(10)]. A breakdown of the company’s investment projects is listed below. When evaluating a new dog food production investment, which cost of capital should be used?1/3 Nuclear Parts Mfr. B=2.01/3 Computer Hard Drive Mfr. B=1.31/3 Dog Food Production B=0.6AVG. B of assets = 1.3Risk