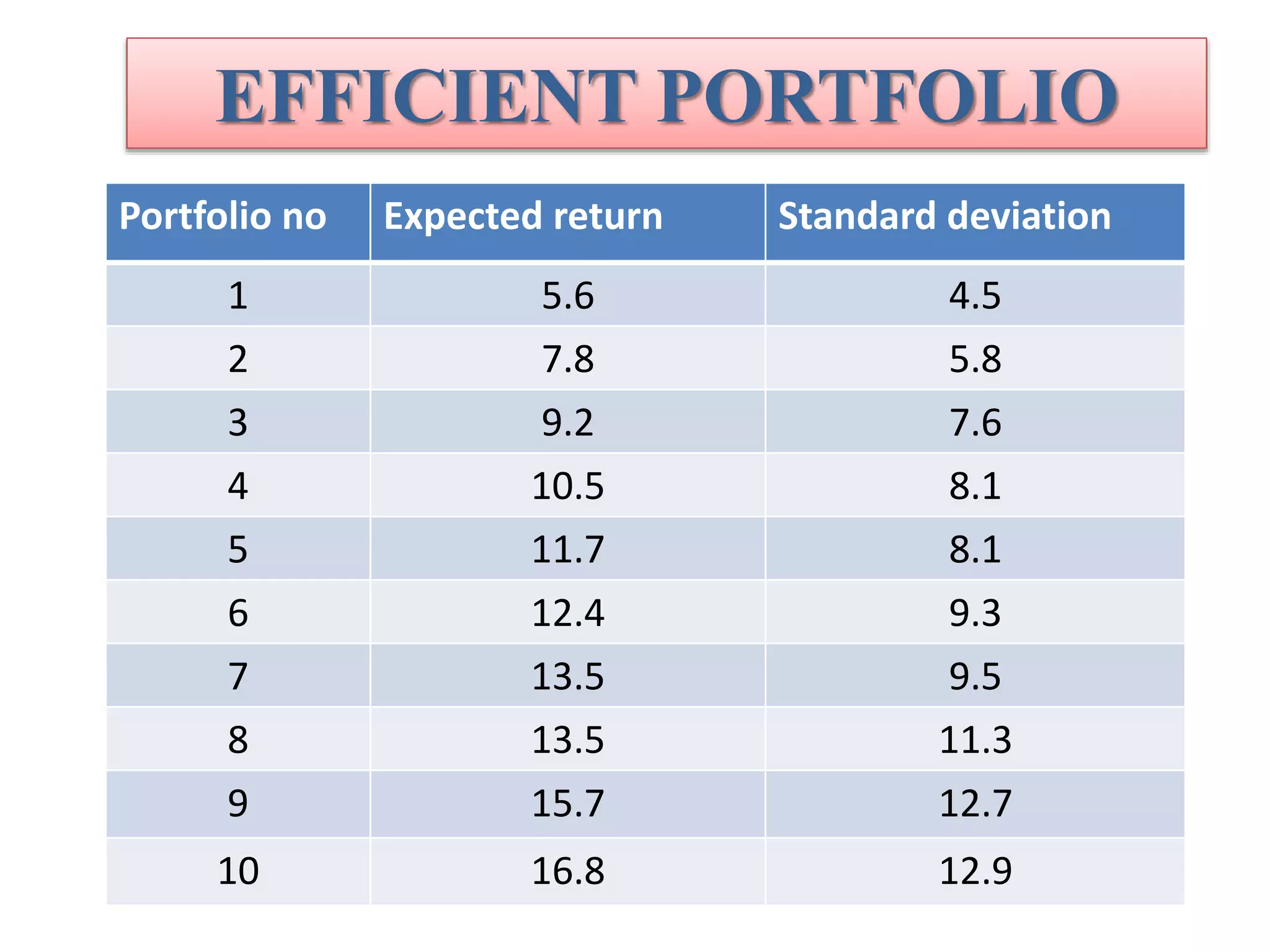
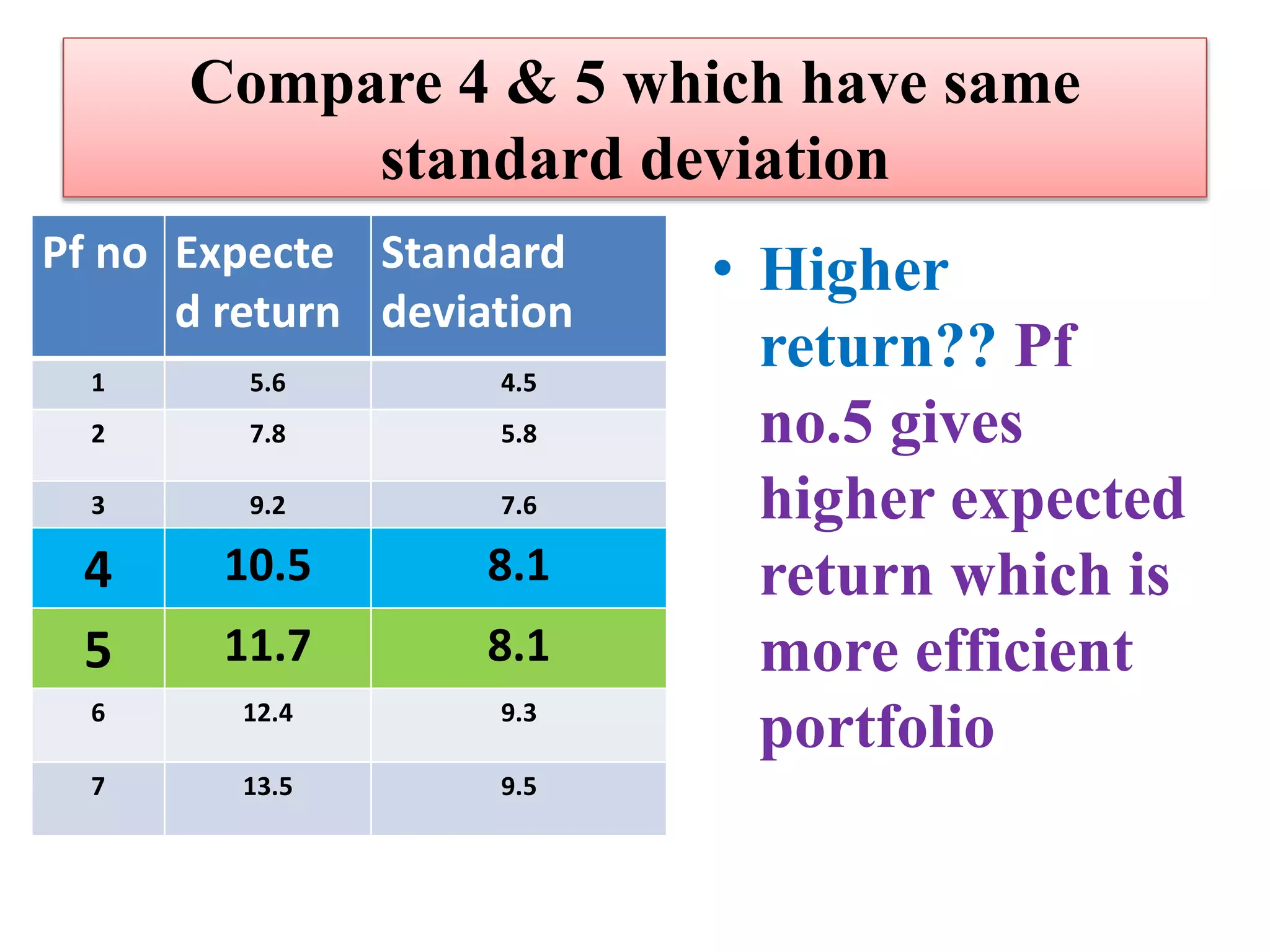
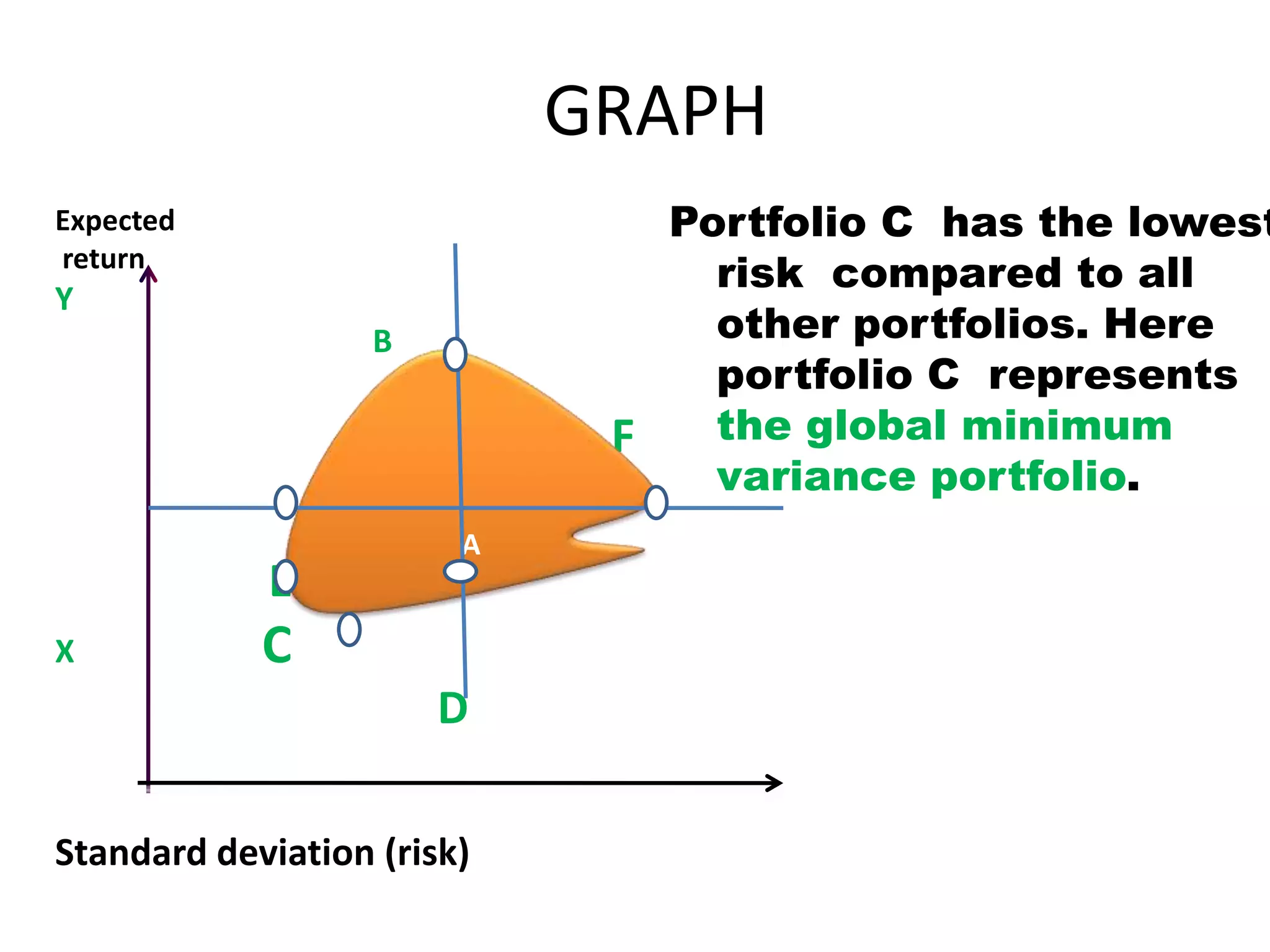
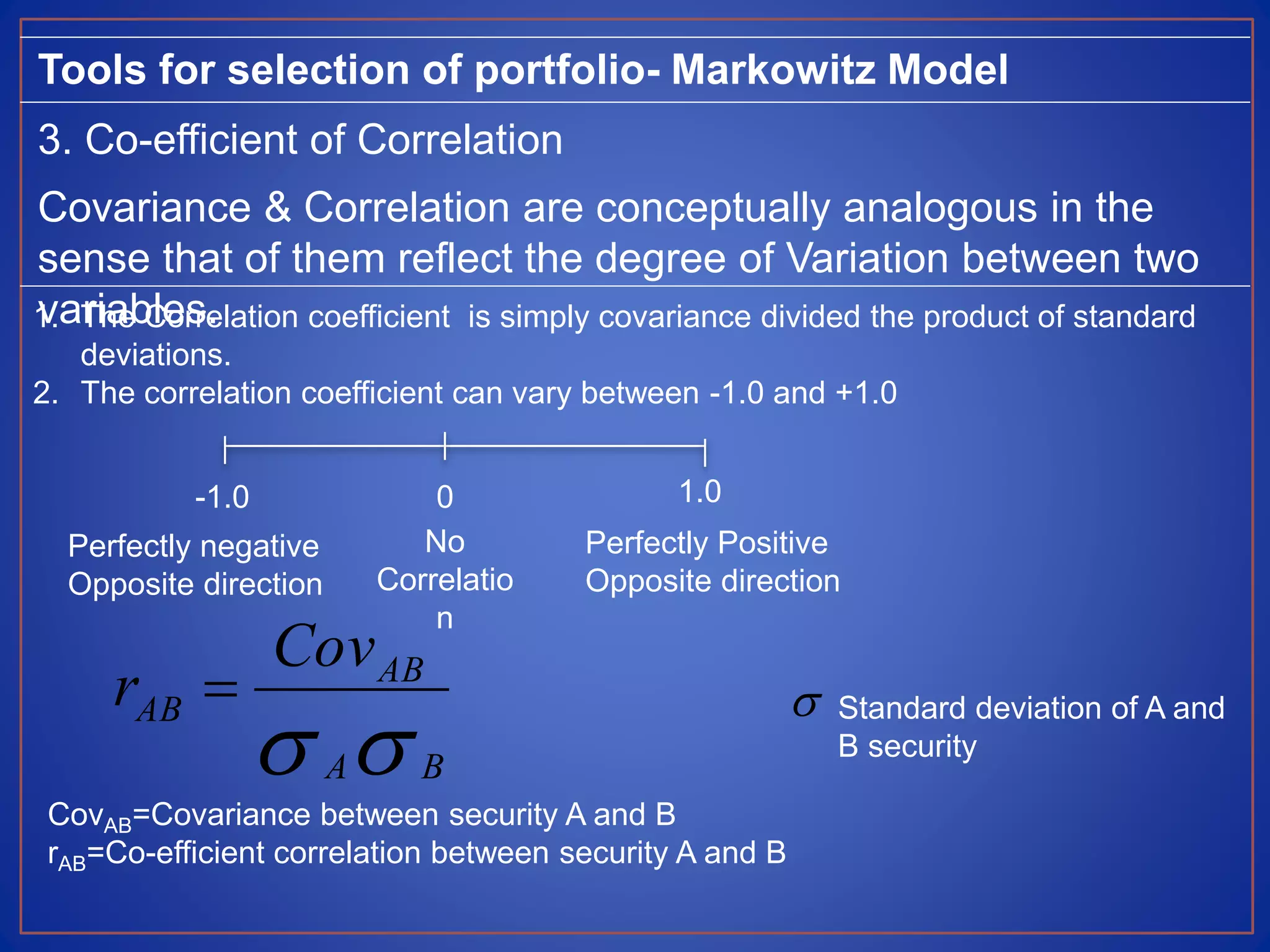
1. The document discusses portfolio selection using the Markowitz model. 2. The Markowitz model aims to find the optimal portfolio, which provides the highest return and lowest risk. It does this by analyzing different combinations of securities to identify efficient portfolios. 3. The document provides details on the tools and steps used in the Markowitz model for portfolio selection, including analyzing expected returns, variance, standard deviation, and coefficients of correlation between securities.

1. PORTFOLIO SELECTION
Submitted to;- Submitted by:-
Dr. Karmpal Sumit
14104024
Vivek
14104025
Mahesh
14104026
Manjeet
14104027

2. Portfolio
• A portfolio is a grouping of financial assets
such as stocks, bonds, cash equivalents as
well as their mutual, exchange –traded and
closed-fund counterparts.
• His choice depends upon the risk-return
characteristics of individual securities.

3. Portfolio Management
Security
Analysis
Portfolio
Analysis
Portfolio
Selection
Portfolio
Revision
Portfolio
Evaluation
1. Fundamental
Analysis
2. Technical
Analysis
3. Efficient
Market
Hypothesis
Diversificatio
n 1. Markowit
z Model
2. Sharpe’s
Single
index
model
3. CAPM
4. APT
1. Formula
Plans
2. Rupee
cost
Averaging
1. Sharpe’s
index
2. Treynor’s
measure
3. Jenson’s
measure

4. Building a Portfolio
• Step-1 : Use the Markowitz portfolio selection
model to identify optimal combinations.
• Step-2 : consider borrowing and lending
possibilities.
• Step-3 : choose the final portfolio based on
your preferences for return relative to risk.

5. PORTFOLIO SELECTION
• Goal: finding the optimal portfolio
• OPTIMAL PORTFOLIO: Portfolio that
provides the highest return and lowest risk.
• Method of portfolio selection: Markowitz
model

6. Portfolio Selection
The proper goal of portfolio construction
would be to generate a portfolio that provides
the highest return and the lowest risk is
called Optimal portfolio.
The process of finding the optimal
portfolio is described as Portfolio selection.

7. Efficient Set of Portfolio
• The concept of efficient portfolio, let us
consider various combinations of securities
and designated them as portfolio 1 to n.
• The risk of these portfolios may be estimated
by measuring the standard deviation of
portfolio returns.

8. Feasible set of portfolio
• Also known as portfolio opportunity set.
• With a limited no of securities an investor
can create a very large no. of portfolios
by combining theses securities in different
proportions.

9. EFFICIENT PORTFOLIO
Portfolio no Expected return Standard deviation
1 5.6 4.5
2 7.8 5.8
3 9.2 7.6
4 10.5 8.1
5 11.7 8.1
6 12.4 9.3
7 13.5 9.5
8 13.5 11.3
9 15.7 12.7
10 16.8 12.9

10. Compare 4 & 5 which have same
standard deviation
Pf no Expecte
d return
Standard
deviation
1 5.6 4.5
2 7.8 5.8
3 9.2 7.6
4 10.5 8.1
5 11.7 8.1
6 12.4 9.3
7 13.5 9.5
• Higher
return?? Pf
no.5 gives
higher expected
return which is
more efficient
portfolio

11. Compare 7 & 8 which have same Expected
return
Pf
no
Expected
return
Standard
deviation
1 5.6 4.5
2 7.8 5.8
3 9.2 7.6
4 10.5 8.1
5 11.7 8.1
6 12.4 9.3
7 13.5 9.5
8 13.5 11.3
9 15.7 12.7
10 16.8 12.9
• Lower standard
deviation??
Pf no.7 which is
more efficient
portfolio

12. CRITERIA: EFFICIENT PROTFOLIO
• Given 2 portfolio with the same expected return, the
investor would prefer the one with the lower risk.
• Given 2 portfolio with the same risk, the investor
would prefer the one with the higher expected return.

13. GRAPH
Expected
return
Y
B
F F
E
C
X D
Standard deviation (risk)
A

14. GRAPH
Expected
return
Y
F F
E
X
Standard deviation (risk)
• Consider E & F –
both have same
return but E has
less risk then
portfolio E would
be preferred

15. GRAPH
Expected
return B
Y
F
E
C
X
Standard deviation (risk)
• Now consider C & E
–both have same
risk but portfolio E
offer more return
then portfolio E
would preferred.

16. GRAPH
Expected
return B
Y
F
C
X
Standard deviation (risk)
• Consider C& A – both
have same return
but C has less risk
then portfolio C
would be preferred
A

17. Result
E F Same return
but
E has less risk
than F
E has preferred C has minimum
risk & B has
Maximum risk
Based on these
we drawing
efficient
frontier.
C E Same risk
But E offer more
return
E has preferred
C A Same return
But
C has less risk
C has preferred
A B Same level of risk
But
B has higher
B has preferred

18. GRAPH
Expected
return
Y
B
F F
E
X C
D
Standard deviation (risk)
Portfolio C has the lowest
risk compared to all
other portfolios. Here
portfolio C represents
the global minimum
variance portfolio.
A

19. GRAPH
Expected
return
Y
B
F F
E
C
X D
Standard deviation (risk)
A
EFFICIENT
FRONTIER

20. • It contain all the
efficient portfolio.
• Lying between the
global minimum
variance portfolio
(risk) & the maximum
return.
C
B

21. • Harry Max Markowitz (born August 24, 1927) is
an American economist.
• He is best known for his pioneering work in
Modern Portfolio Theory.
• Harry Markowitz put forward this model in
1952.
• Studied the effects of asset risk, return,
correlation and diversification on probable
investment portfolio returns.
Harry Max Markowitz
Essence of Markowitz Model
“Do not put all your eggs in one
basket”1. An investor has a certain amount of capital he wants to invest over a single time
horizon.
2. He can choose between different investment instruments, like stocks, bonds,
options, currency, or portfolio. The investment decision depends on the future risk
and return.
3. The decision also depends on if he or she wants to either maximize the yield or

22. Essence of Markowitz Model
1. Markowitz model assists in the selection of the most efficient by analysing
various possible portfolios of the given securities.
2. By choosing securities that do not 'move' exactly together, the HM model
shows investors how to reduce their risk.
3. The HM model is also called Mean-Variance Model due to the fact that it is
based on expected returns (mean) and the standard deviation (variance) of
the various portfolios.
Diversification and Portfolio Risk
PortfolioRisk
Number of Shares
5 10 15 20
Total
Risk
S
R
US
R
p p deviationstandardthe
SR: Systematic Risk
USR: Unsystematic Risk

23. • An investor has a certain amount of capital he wants to
invest over a single time horizon.
• He can choose between different investment instruments,
like stocks, bonds, options, currency, or portfolio.
• The investment decision depends on the future risk and
return.
• The decision also depends on if he or she wants to either
maximize the yield or minimize the risk.
• The investor is only willing to accept a higher risk if he or
she gets a higher expected return.

24. Tools for selection of portfolio- Markowitz Model
1. Expected return (Mean)
Mean and average to refer to the sum of all values divided
by the total number of values.
The mean is the usual average, so:
(13 + 18 + 13 + 14 + 13 + 16 + 14 + 21 + 13) ÷ 9 = 15
)((ER)ReturnExpected
1
i

n
i
i REW
Where:
ER = the expected return on Portfolio
E(Ri) = the estimated return in scenario i
Wi= weight of security i occurring in the port folio
Rp=R1W1+R2W2………..
n Rp = the expected return on Portfolio
R1 = the estimated return in Security 1
R2 = the estimated return in Security 1
W1= Proportion of security 1 occurring in the port folio
W2= Proportion of security 1 occurring in the port folio
Where:
1. Expected return (Mean)
2. Standard deviation (variance)
3. Co-efficient of Correlation

25. Tools for selection of portfolio- Markowitz Model
2. Variance & Co-variance
The variance is a measure of how far a set of numbers is
spread out. It is one of several descriptors of a probability
distribution, describing how far the numbers lie from the mean
(expected value).
1. Covariance reflects the degree to which the returns of the two securities vary or
change together.
2. A positive covariance means that the returns of the two securities move in the
same direction.
3. A negative covariance implies that the returns of the two securities move in
opposite direction.
Co-variance
)-)(R(Prob
1 _
1i
_
i BB
n
AAAB RRR
N
COV 

2
_
2
1i
_
i )-(R)(Probariance BB
n
AA RRRV  
CovAB=Covariance between security A and B
RA=Return on security A
RB=Return on Security B
_
AR
_
BR
=Expected Return on security A
=Expected Return on security B

26. Tools for selection of portfolio- Markowitz Model
3. Co-efficient of Correlation
Covariance & Correlation are conceptually analogous in the
sense that of them reflect the degree of Variation between two
variables.1. The Correlation coefficient is simply covariance divided the product of standard
deviations.
2. The correlation coefficient can vary between -1.0 and +1.0
CovAB=Covariance between security A and B
rAB=Co-efficient correlation between security A and B
-1.0 0 1.0
Perfectly negative
Opposite direction
Perfectly Positive
Opposite direction
No
Correlatio
n
 BA
AB
AB
Cov
r   Standard deviation of A and
B security

27. CHAPTER 8 – Risk, Return and Portfolio Theory
Time 0 1 2
If returns of A and B are
perfectly negatively correlated,
a two-asset portfolio made up
of equal parts of Stock A and B
would be riskless. There would
be no variability
of the portfolios returns over
time.
Returns on Stock A
Returns on Stock B
Returns on Portfolio
Returns
%
10%
5%
15%
20%

28. CHAPTER 8 – Risk, Return and Portfolio Theory
Time 0 1 2
If returns of A and B are
perfectly positively correlated,
a two-asset portfolio made up
of equal parts of Stock A and B
would be risky. There would be
no diversification (reduction of
portfolio risk).
Returns
%
10%
5%
15%
20%
Returns on Stock A
Returns on Stock B
Returns on Portfolio

29. • The riskiness of a portfolio that is made of different risky assets is a
function of three different factors:
• the riskiness of the individual assets that make up the portfolio
• the relative weights of the assets in the portfolio
• the degree of variation of returns of the assets making up the portfolio
• The standard deviation of a two-asset portfolio may be measured
using the Markowitz model:
BAABBABBAAp rwwww  22222

CACACACBCBCBBABABACCBBAAp rwwrwwrwwwww  ,,,
222222
222 
The data requirements for a three-asset portfolio grows dramatically if we are
using Markowitz Portfolio selection formulae.
We need 3 (three) correlation coefficients between A and B; A and C; and B
and C.
A
B C
ρa,b
ρb,c
ρa,c

30. • The optimal portfolio concept falls under the modern
portfolio theory. The theory assumes that investors
fanatically try to minimize risk while striving for the
highest return possible.

31. • WHAT IS A RISK FREE ASSET?
• DEFINITION: an asset whose terminal value is
certain
• variance of returns = 0,
• covariance with other assets = 0
0i
jiijij  
0
If
then

32. 32
• INVESTING IN BOTH: RISKFREE AND RISKY ASSET
PORTFOLIOS X1 X2 ri di
A .00 1.0 4 0
B .25 .75 7.05 3.02
C .50 .50 10.10 6.04
D .75 .25 13.15 9.06
E 1.00 .00 16.20 12.08

33. 33
• RISKY AND RISK FREE PORTFOLIOS
A
D
rRF = 4% P
rP
0
C
B
E

34. • IN RISKY AND RISK FREE PORTFOLIOS
• All portfolios lie on a straight line
• Any combination of the two assets lies on a straight line
connecting the risk free asset and the efficient set of the risky
assets
• The Connection to the Risky
Portfolio
rP
P0

35. 35
• The Connection to the Risky Portfolio
rP
P0
S
R
P

36. 36