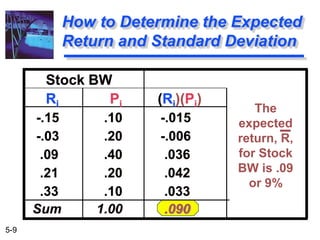
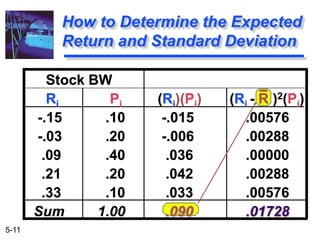
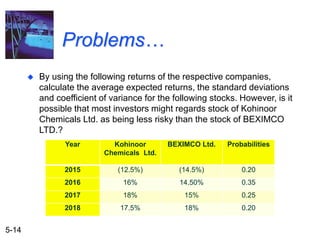
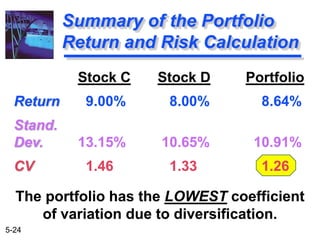
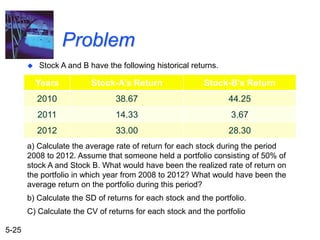
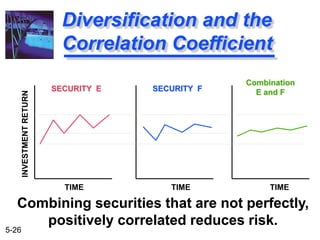
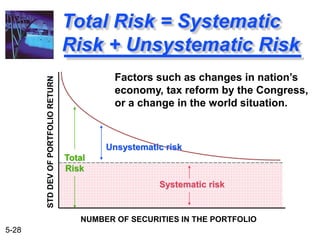
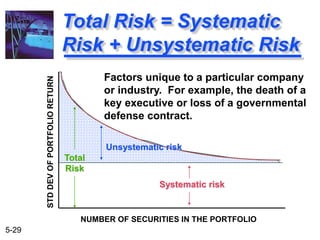
The document explains the concepts of risk and return in investment, detailing how to measure them through expected return, standard deviation, and coefficient of variation. It differentiates between avoidable (unsystematic) and unavoidable (systematic) risks and emphasizes the importance of diversification in managing these risks. Additionally, it covers portfolio management techniques, including calculations for expected return and standard deviation for different portfolio compositions.

1. 5-1
Chapter 3
Risk and
Return

2. 5-2
After studying this Chapter,
you should be able to:
1. Understand the relationship (or “trade-off”) between
risk and return.
2. Define risk and return and show how to measure
them by calculating expected return, standard
deviation, and coefficient of variation.
3. Explain risk and return in a portfolio context, and
distinguish between individual security and portfolio
risk.
4. Distinguish between avoidable (unsystematic) risk
and unavoidable (systematic) risk and explain how
proper diversification can eliminate one of these
risks.

3. 5-3
Risk and Return
Defining Risk and Return
Using Probability Distributions to
Measure Risk
Risk and Return in a Portfolio Context
Diversification

4. 5-4
Defining Return
Income received on an investment
plus any change in market price,
usually expressed as a percent of
the beginning market price of the
investment.
Dt + (Pt - Pt-1 )
Pt-1
R =

5. 5-5
Return Example
The stock price for Stock A was $10 per
share 1 year ago. The stock is currently
trading at $9.50 per share and shareholders
just received a $1 dividend. What return
was earned over the past year?

6. 5-6
Return Example
The stock price for Stock A was $10 per
share 1 year ago. The stock is currently
trading at $9.50 per share and shareholders
just received a $1 dividend. What return
was earned over the past year?
$1.00 + ($9.50 - $10.00 )
$10.00R = = 5%

7. 5-7
Defining Risk
What rate of return do you expect on your
investment (savings) this year?
What rate will you actually earn?
Does it matter if it is a bank CD or a share
of stock?
The variability of returns from
those that are expected.

8. 5-8
Determining Expected
Return (Discrete Dist.)
R = S ( Ri )( Pi )
R is the expected return for the asset,
Ri is the return for the ith possibility,
Pi is the probability of that return
occurring,
n is the total number of possibilities.
n
i=1

9. 5-9
How to Determine the Expected
Return and Standard Deviation
Stock BW
Ri Pi (Ri)(Pi)
-.15 .10 -.015
-.03 .20 -.006
.09 .40 .036
.21 .20 .042
.33 .10 .033
Sum 1.00 .090
The
expected
return, R,
for Stock
BW is .09
or 9%

10. 5-10
Determining Standard
Deviation (Risk Measure)
s = S ( Ri - R )2( Pi )
Standard Deviation, s, is a statistical
measure of the variability of a distribution
around its mean.
It is the square root of variance.
Note, this is for a discrete distribution.
n
i=1

11. 5-11
How to Determine the Expected
Return and Standard Deviation
Stock BW
Ri Pi (Ri)(Pi) (Ri - R )2(Pi)
-.15 .10 -.015 .00576
-.03 .20 -.006 .00288
.09 .40 .036 .00000
.21 .20 .042 .00288
.33 .10 .033 .00576
Sum 1.00 .090 .01728

12. 5-12
Determining Standard
Deviation (Risk Measure)
s = S ( Ri - R )2( Pi )
s = .01728
s = .1315 or 13.15%
n
i=1

13. 5-13
Coefficient of Variation
The ratio of the standard deviation of
a distribution to the mean of that
distribution.
It is a measure of RELATIVE risk.
CV = s / R
CV of BW = .1315 / .09 = 1.46

14. 5-14
Problems…
 By using the following returns of the respective companies,
calculate the average expected returns, the standard deviations
and coefficient of variance for the following stocks. However, is it
possible that most investors might regards stock of Kohinoor
Chemicals Ltd. as being less risky than the stock of BEXIMCO
LTD.?
Year Kohinoor
Chemicals Ltd.
BEXIMCO Ltd. Probabilities
2015 (12.5%) (14.5%) 0.20
2016 16% 14.50% 0.35
2017 18% 15% 0.25
2018 17.5% 18% 0.20

15. 5-15
RP = S ( Wj )( Rj )
RP is the expected return for the portfolio,
Wj is the weight (investment proportion)
for the jth asset in the portfolio,
Rj is the expected return of the jth asset,
m is the total number of assets in the
portfolio.
Determining Portfolio
Expected Return
m
j=1

16. 5-16
Determining Portfolio
Standard Deviation
m
j=1
m
k=1
sP = S S Wj Wk sjk
Wj is the weight (investment proportion)
for the jth asset in the portfolio,
Wk is the weight (investment proportion)
for the kth asset in the portfolio,
sjk is the covariance between returns for
the jth and kth assets in the portfolio.

17. 5-17
You are creating a portfolio of Stock D and Stock
BW (from earlier). You are investing $2,000 in
Stock BW and $3,000 in Stock D. Remember that
the expected return and standard deviation of
Stock BW is 9% and 13.15% respectively. The
expected return and standard deviation of Stock D
is 8% and 10.65% respectively. The correlation
coefficient between BW and D is 0.75.
What is the expected return and standard
deviation of the portfolio?
Portfolio Risk and
Expected Return Example

18. 5-18
Determining Portfolio
Expected Return
WBW = $2,000 / $5,000 = .4
WD = $3,000 / $5,000 = .6
RP = (WBW)(RBW) + (WD)(RD)
RP = (.4)(9%) + (.6)(8%)
RP = (3.6%) + (4.8%) = 8.4%

19. 5-19
Two-asset portfolio:
Col 1 Col 2
Row 1 WBW WBW sBW,BW WBW WD sBW,D
Row 2 WD WBW sD,BW WD WD sD,D
This represents the variance - covariance
matrix for the two-asset portfolio.
Determining Portfolio
Standard Deviation

20. 5-20
Two-asset portfolio:
Col 1 Col 2
Row 1 (.4)(.4)(.0173) (.4)(.6)(.0105)
Row 2 (.6)(.4)(.0105) (.6)(.6)(.0113)
This represents substitution into the
variance - covariance matrix.
Determining Portfolio
Standard Deviation

21. 5-21
Two-asset portfolio:
Col 1 Col 2
Row 1 (.0028) (.0025)
Row 2 (.0025) (.0041)
This represents the actual element values
in the variance - covariance matrix.
Determining Portfolio
Standard Deviation

22. 5-22
Determining Portfolio
Standard Deviation
sP = .0028 + (2)(.0025) + .0041
sP = SQRT(.0119)
sP = .1091 or 10.91%
A weighted average of the individual
standard deviations is INCORRECT.

23. 5-23
Determining Portfolio
Standard Deviation
The WRONG way to calculate is a
weighted average like:
sP = .4 (13.15%) + .6(10.65%)
sP = 5.26 + 6.39 = 11.65%
10.91% = 11.65%
This is INCORRECT.

24. 5-24
Stock C Stock D Portfolio
Return 9.00% 8.00% 8.64%
Stand.
Dev. 13.15% 10.65% 10.91%
CV 1.46 1.33 1.26
The portfolio has the LOWEST coefficient
of variation due to diversification.
Summary of the Portfolio
Return and Risk Calculation

25. 5-25
Problem
 Stock A and B have the following historical returns.
a) Calculate the average rate of return for each stock during the period
2008 to 2012. Assume that someone held a portfolio consisting of 50% of
stock A and Stock B. What would have been the realized rate of return on
the portfolio in which year from 2008 to 2012? What would have been the
average return on the portfolio during this period?
b) Calculate the SD of returns for each stock and the portfolio.
C) Calculate the CV of returns for each stock and the portfolio
Years Stock-A’s Return Stock-B’s Return
2010 38.67 44.25
2011 14.33 3.67
2012 33.00 28.30

26. 5-26
Combining securities that are not perfectly,
positively correlated reduces risk.
Diversification and the
Correlation Coefficient
INVESTMENTRETURN
TIME TIMETIME
SECURITY E SECURITY F
Combination
E and F

27. 5-27
Systematic Risk is the variability of return
on stocks or portfolios associated with
changes in return on the market as a whole.
Unsystematic Risk is the variability of return
on stocks or portfolios not explained by
general market movements. It is avoidable
through diversification.
Total Risk = Systematic
Risk + Unsystematic Risk
Total Risk = Systematic Risk +
Unsystematic Risk

28. 5-28
Total Risk = Systematic
Risk + Unsystematic Risk
Total
Risk
Unsystematic risk
Systematic risk
STDDEVOFPORTFOLIORETURN
NUMBER OF SECURITIES IN THE PORTFOLIO
Factors such as changes in nation’s
economy, tax reform by the Congress,
or a change in the world situation.

29. 5-29
Total Risk = Systematic
Risk + Unsystematic Risk
Total
Risk
Unsystematic risk
Systematic risk
STDDEVOFPORTFOLIORETURN
NUMBER OF SECURITIES IN THE PORTFOLIO
Factors unique to a particular company
or industry. For example, the death of a
key executive or loss of a governmental
defense contract.