Download as PPS, PPTX
![Kalkulus2-unpad 65
Operasi pada Deret Kuasa
∑
∞
=
=
0
)(
n
n
n xaxS
[ ] ...)()(')( 3
3
2
210
0
++++== ∑
∞
=
xaxaxaaDxaDxSi x
n
n
nx
∑
∞
=
−
=
1
1
n
n
n xna
∫
x
dttSii
0
)()( ∑∫
∞
=
=
0
0
n
x
n
n dtta ∑
∞
=
+
+
=
0
1
1n
nn
x
n
a
Misal
maka](https://image.slidesharecdn.com/2-180712075816/85/Barisan-dan-Deret-Kalkulus-2-65-320.jpg)
Uploaded byKelinci Coklat
Barisan dan Deret ( Kalkulus 2 )
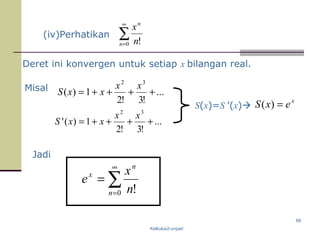
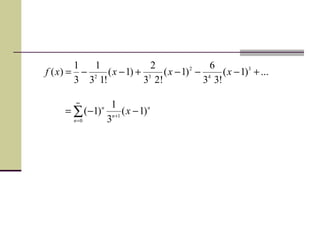Dokumen ini membahas tentang barisan dan deret dalam kalkulus, termasuk definisi barisan tak hingga, konvergensi, dan contoh nyata dari deret konvergen dan divergen. Selain itu, penjelasan mengenai sifat-sifat kekonvergenan deret tak hingga serta uji kekonvergenannya juga disampaikan. Terdapat berbagai contoh dan latihan untuk memahami konsep-konsep tersebut.
More Related Content
![Persamaan Diferensial [orde-2]](https://cdn.slidesharecdn.com/ss_thumbnails/persamaandiferensialorde-2-150706213036-lva1-app6892-thumbnail.jpg?width=640&height=640&fit=bounds)
Similar to Barisan dan Deret ( Kalkulus 2 )
![[Sub Pokok Bahasan 4] Kekonvergenan barisan dan uji deret positif dan Uji kek...](https://cdn.slidesharecdn.com/ss_thumbnails/subpokokbahasan4kekonvergenanbarisandanujideretpositifdanujikekonvergenanderetgantitandav2-231029111956-1949a611-thumbnail.jpg?width=640&height=640&fit=bounds)
Barisan dan Deret ( Kalkulus 2 )
- 1.
- 2. Kalkulus2-unpad 2 Barisan Tak Hingga Definisi Barisan Tak Hingga adalah fungsi dengan daerah asal bilangan asli(N). Notasi: f : N R Fungsi tersebut dikenal sebagai barisan bilangan Real. Biasa ditulis {an} atau dengan an adalah suku ke-n. Bentuk penulisan dari barisan : 1. bentuk eksplisit suku ke-n : 2. ditulis sejumlah berhingga suku awalnya. 3. bentuk rekursif n n n a a aa + == + 1 ,1 11 n an 1 = ( ) nanfn = { } 1= ∞ nn a
- 3. Kalkulus2-unpad 3 Kekonvergenan Barisan Definisi: Barisan { an} dikatakan konvergen ke L ditulis Sebaliknya, barisan yang tidak konvergen ke suatu bilangan L yang berhingga, maka barisan dikatakan divergen (dalam hal ini mungkin atau beroksilasi) Lan n = ∞→ lim ε<−⇒≥ LaNn n ∋∃>∀ Naslibilangan,0εJika ∞−∞ ,
- 4. Kalkulus2-unpad 4 Sifat BarisanKonvergen Jika barisan {an} konvergen ke L dan barisan {bn} konvergen ke M, maka 1. 2. 3. , untuk M 0 Barisan {an} dikatakan a. Monoton naik jika an+1 > an b. Monoton turun jika an+1 < an
- 5. Kalkulus2-unpad 5 Contoh 1. konvergen ke½. Jawab: Karena { } + = 12n n an Periksa kekonvergenan barisan berikut . 2 1 1 2 )1( lim 12 limlim = + = + = ∞→∞→∞→ n n n n n a nnnn , maka +12n n 2 1 lim = ∞→ nn a
- 6. Kalkulus2-unpad 6 Contoh 2. divergen. Jawab: Karena Periksa kekonvergenanbarisan berikut , maka { } + = 3n n an . 3 1 lim 3 1 )( lim 3 limlim ∞= + = + = + = ∞→∞→∞→∞→ n n n n nn n n a nnn n n ∞=∞→ n n alim + 3n n
- 7. Kalkulus2-unpad 7 Catatan Akandijumpai banyak persoalan konvergensi barisan yang tidak bisa langsung dicari limit tak hingga suku ke – nnya. Untuk itu kita dapat menghitung limit di tak hingga dari fungsi yang sesuai. Fakta ini digunakan sebagai penyederhanaan karena kita dapat memakai kaidah L’Hopital untuk soal peubah kontinu. Lxf x = ∞→ )(limJika Lan n = ∞→ lim, maka Teorema: Misalkan memenuhi1),( ≥= xxfy nanf =)(
- 8. Kalkulus2-unpad 8 ee x x x == + = ∞→ 1 1 limexp n n n 1 1a += Jawab: Ambil x x xf += 1 1)( , sehingga maka dikatakan += ∞→ x x x 1 1ln.limexp + = ∞→ x x x /1 ))/1(1ln( limexp x x x + ∞→ 1 1lim ) 1 ( ) 1 ( 1limexp 2 2 x xx x x − − += ∞→ Contoh Periksa kekonvergenan n n + 1 1 =∞→ )(lim xfx Karena ,lim)(lim eaxf nnx == ∞→∞→ n n + 1 1 konvergen ke e.
- 9. Kalkulus2-unpad 9 Latihan { } +− + = 32 14 2 2 nn n an {} + + = 1 23 2 n n an { } + = 1n n an { } = n n an )ln( ... 5 4 , 4 3 , 3 2 , 2 11. 2. 8. 7. 6. 5. 4. 3. Periksa kekonvergenan dari barisan berikut: { } = n nan π sin { } = n n n a 4 π { } { }nnan −= 2 { } + = nn n an π sin 12 2 9. { } + = n nn n e ee a 2 2 2 .10
- 10. Kalkulus2-unpad 10 Deret TakHingga Bentuk deret tak hingga dinotasikan dengan notasi sigma, sebagai berikut: dengan an adalah suku ke-n. Kekonvergenan suatu deret ditentukan dari barisan jumlah parsialnya. ......321 1 +++++=∑ ∞ = n i i aaaaa
- 11. Kalkulus2-unpad 11 Barisan JumlahParsial Misalkan Sn menyatakan jumlah parsial ke-n suku dari deret , maka∑ ∞ =1i ia {Sn}, dinamakan barisan jumlah parsial deret . 1 ∑ ∞ =i i a Dari jumlah parsial ini didapat bahwa Sn – Sn-1 = an. ∑= =++++= n i inn aaaaaS 1 321 ... 11 aS = 212 aaS += . . .
- 12. Kalkulus2-unpad 12 Kekonvergenan DeretTak Hingga Deret tak hingga ∑ ∞ =1n na konvergen dan mempunyai jumlah S jika barisan jumlah parsialnya ({Sn}) konvergen ke S (artinya divergen maka deret divergen. SSn n = ∞→ lim ), sebaliknya jika { }n S
- 13. Kalkulus2-unpad 13 Deret Geometri Bentuk umum deret geometri : dengan a ≠ 0. Jumlah parsial deret ini adalah Sehingga n n ararararrS ++++= ...32 n n araSr −=− )1( . 1 r ara S n n − − = 1 2 3 1 1 ...i i i ar a ar ar ar ar ∞ − − = = + + + + +∑ 12 1 1 ... − = − ++++== ∑ n n i i n arararaarS
- 14. Kalkulus2-unpad 14 ≥∞+ < −= − − = ∞→∞→ 1; 1; 1 1 limlim r r r a r ara S n n n n Jadi, deretgeometri konvergen jika 1<r dengan jumlah . 11 1 1 r a aratau r a S i i − = − = ∑ ∞ = −
- 15. Kalkulus2-unpad 15 Contoh Selidiki kekonvergenanderet ... 32 1 16 1 8 1 4 1 2 1 +++++1. Jawab: Kalau kita perhatikan, deret ini adalah deret geometri dengan rasio ½ ( r<1). Sehingga deret ini konvergen dengan jumlah .1 2/11 2/1 = − =S
- 16. Kalkulus2-unpad 16 ∑ ∞ = +1)1( 1 i ii Jawab: Kalau kita perhatikan dan Karena barisan jumlah parsialnya konvergen ke 1, maka deret di atas juga konvergen dengan jumlah 1. Dari sini kita peroleh bahwa jumlah parsial ke-n-nya Sn = = = = 1 (Deret Kolaps)2. Selidi kekonvergenan deret ∑ ∑ ∞ = ∞ = + −= +1 1 1 11 )1( 1 i i iiii
- 17. Kalkulus2-unpad 17 3.3. Jawab: Dari sinikita dapatkan Jadi deret harmonik adalah deret divergen. ∑ ∞ =1 1 i i Sn = 1 + Sn = 1 + ≥ 1 + = 1 + (Deret Harmonik) ∞=∞→ n n SlimSehingga
- 18. Kalkulus2-unpad 18 Sifat-sifat derettak hingga ∑ ∞ =1n na konvergen maka 0lim = ∞→ n n a 0lim ≠ ∞→ n n a maka deret divergen ). Contoh: Buktikan bahwa ∑ ∞ = ++1 2 2 433n nn n divergen. Bukti: = ++ = ∞→∞→ 433 limlim 2 2 nn n a nnn 0 3 1 43 3 1 lim 2 ≠= ++ ∞→ nn n Karena divergen.∑ ∞ = ++1 2 2 433n nn n Jika (jika 1. Uji kedivergenan suku ke-n ,0 3 1 lim ≠= ∞→ n n a maka
- 19. Kalkulus2-unpad 19 2. Sifatlinear Jika ∑ ∑ nn bdana konvergen dan c konstanta, maka )(∑ ∑ ± nnn badanca konvergen, dan ∑ ∑ ∑ ∑ ∑ ±=± = nnnn nn babaii accai )( )( 3. Jika ∑ na divergen dan c konstanta, maka ∑ nca divergen.
- 20. Kalkulus2-unpad 20 Uji Kekonvergenan DeretPositif Misalkan f fungsi kontinu, positif dan monoton turun pada selang [1,∝). Andaikan ∫ ∞ 1 )( dxxf∑ ∞ =1n na konvergen 1. Uji Integral Nnnfan ∈= ),( maka ⇔ konvergen ∑ ∞ =1n na
- 21. Kalkulus2-unpad Contoh 1. Selidiki kekonvergenandari ∑ ∞ = − 1n n2 en Jawab: ambil .)( 2 x exxf − = dxex x2 1 −∞ ∫ =− ∞→ ∫ dxex x b b 2 1 lim ∫ − ∞→ b x b xde 1 2 )(lim 2 1 2 b x b e 1 2 lim 2 1 − ∞→ −= ) 11 (lim 2 1 2 eebb −−= ∞→ e2 1 = = Karena dxex x2 1 − ∞ ∫ konvergen, maka ∑ ∞ = − 1 2 n n en konvergen. f kontinu, positif , turun di (buktikan sendiri !), maka 21 ),1[ ∞
- 22. Kalkulus2-unpad 22 Contoh 2. Selidikikekonvergenan dari Jawab: ambil , kontinu,positif,turun di Karena divergen, maka divergen. ∑ ∞ =2 ln 1 n nn xx xf ln 1 )( = ∫∫ ∞→ ∞ = b b xx dx xx dx 22 ln lim ln 2 (ln ) lim ln b b d x x→∞ = ∫ ( ) ( ) ( ) ∞=−== ∞→∞→ 2lnlnlnlnlimlnlnlim bx bb ∫ ∞ 2 ln xx dx ∑ ∞ =2n nlnn 1 ),2[ ∞
- 23. Kalkulus2-unpad 23 Latihan ∑ ∞ =2n 2 nlnn 1 ∑ ∞ = +1n1n2 1 ∑ ∞ = +1n 2 1n4 1 ( ) ∑ ∞ = +1n 2 3 n34 1 3. 2. 4. 5. 1. Selidiki kekonvergenan deret berikut: ( )∑ ∞ = −3n 2 2n 1 6. Tentukan syarat k agar deret 0, ln 1 2 >∑ ∞ = k nnn k konvergen.
- 24. Kalkulus2-unpad 24 Uji DeretPositif 2. Uji Deret -p Deret-p berbentuk . 1 1 ∑ ∞ =n p n dengan menggunakan uji integral, kita dapatkan =∫ ∞ ∞→ dx xpt 1 1 lim p t p t − − = − ∞→ 1 1 lim 1 <≤∞ > − − = 10; 1; 1 1 p p p Jika p<0 Jika . 1 lim ∞= ∞→ pn n Maka deret divergen. ,0≥p Sehingga ∑ ∞ =1 1 n p n konvergen jika p>1 dan divergen jika .1≤p ≠ − =∞= − ∞→ ∞→ 1; 11 lim 1; 1 lnlim 1 p t p x p t x p t t
- 25. Kalkulus2-unpad 25 Contoh Apakah deretberikut konvergen atau divergen? 1. ∑ ∞ =1 001,1 1 n n Berdasarkan uji deret-p, deret ∑ ∞ =1 001,1 1 n n konvergen karena p=1,001 > 1 2. Berdasarkan uji deret-p, deret divergen karena p= ½ < 1 ∑ ∞ =1 2 1 1 n n ∑ ∞ =1 2 1 1 n n
- 26. Kalkulus2-unpad 26 Uji DeretPositif 3. Uji banding biasa Andaikan ∑ ∞ = `1n na ∑ ∞ = `1n nbdan deret positif, maka 1. Jika konvergen, maka ∑ ∞ = `1n na ∑ ∞ = ≥ `1 dan n nnn bab ∑ ∞ = ≤ `1 dan n nnn bab ∑ ∞ = `1n na konvergen. 2. Jika divergen, maka divergen.
- 27. Kalkulus2-unpad 27 Contoh 1. SelidikiKekonvergenan deret ∑ ∞ = −3 2 5n n n Jawab: Bandingkan dengan 52 − = n n an Perhatikan bahwa . 5 1 atau 5 222 − < − < n n nn n n n Karena ∑ ∞ =1n n 1 ∑ ∞ = −3 2 5n n n deret divergen(harmonik), maka juga deret yang divergen. nn n bn 1 2 ==
- 28. Kalkulus2-unpad 28 Jawab: Bandingkan dengan konvergen. ∑ ∞ =+1 2 53 1 n n 2 1 1 3 5n n ∞ = + ∑ 5 11 . 3 1 3 1 222 + >= nnn 53 1 2 + = n an 2 1 1 n n ∞ = ∑ Perhatikan bahwa Karena konvergen dengan uji deret-p (p=2) maka 2. Selidiki kekonvergenan deret 2 1 n bn =
- 29. Kalkulus2-unpad 29 Latihan Selidiki kekonvergenanderet berikut : ∑ ∞ = +1 5 2 5n n n ∑ ∞ = −6 5 1 n n ∑ ∞ = +1n n 12 1 ∑ ∞ = + 1 2 cos6 n n n ∑ ∞ = −1n 1n2 12. 4. 5. 3. 1. ∑ ∞ = −1 1 .6 n n n
- 30. Kalkulus2-unpad 30 4. UjiBanding limit Andaikan dan deret positif dan n n n b a L ∞→ = lim Uji Deret Positif 1. Jika 0 < L < ∞ maka ∑ ∞ = `1n na ∑ ∞ = `1n nbdan sama-sama konvergen atau divergen. 2. Jika L = 0 dan ∑ ∞ = `1n nb ∑ ∞ = `1n na konvergen maka konvergen. ∑ ∞ = `1n na ∑ ∞ = `1n nb
- 31. Kalkulus2-unpad 31 Contoh Selidiki kekonvergenandari deret berikut : ∑ ∞ = +− + 1 23 75 32 .1 n nn n Gunakan Uji Banding Limit. sehingga Pilih lim n n n a L b→∞ = ∑ ∞ = +− + 1n 23 7n5n 3n2 konvergen. = 2 Karena L=2 dan Jawab: 2 1 n bn = 2 23 1 75 32 lim n nn n n +− + = ∞→ 75 32 lim 23 23 +− + = ∞→ nn nn n konvergen dengan uji deret-p, maka ∑∑ = 2 1 n bn
- 32. Kalkulus2-unpad 32 Gunakan UjiBanding Limit. sehingga Pilih lim n n n a L b→∞ = divergen. Karena L=1 dan Jawab: divergen (deret harmoik), ∑ ∞ = +1 2 4 1 .2 n n ∑ ∞ = +1n 2 4n 1 n bn 1 = n n n 1 4 1 lim 2 += ∞→ 1 4 lim 2 2 = + = ∞→ n n n ∑ ∞ =1 1 n n maka
- 33. Kalkulus2-unpad 33 Latihan Selidiki kekonvergenandari deret berikut: ∑ ∞ = ++1n 2 3n2n n ∑ ∞ = − + 1n 3 4n 1n3 ∑ ∞ = +1n 1nn 1 ∑ ∞ = + 1n 2 n 3n2 ∑ ∞ =1n 2 n nln2. 4. 5. 3. 1. ∑ ∞ = −1 12 1 .6 n n
- 34. Kalkulus2-unpad 34 5. UjiHasil Bagi Uji Deret Positif ∑ ∞ =1n na n n n a a 1 lim + ∞→ =ρ Diketahui merupakan suatu deret dengan ρ ∑ ∞ =1n na1. Jika < 1 maka deret konvergen suku-suku yang positif, dan ρ ∑ ∞ =1n na divergen2. Jika > 1 maka deret ρ = 1 maka tidak dapat diambil kesimpulan.3. Jika
- 35. Kalkulus2-unpad 35 Contoh Selidiki kekonvergenanderet berikut: 1. ∑ ∞ =1 ! 3 n n n ⇒= ! 3 n a n n ( )!1 3 1 1 + = + + n a n n sehingga Karena ∑ ∞ =1 ! 3 n n n konvergen. Jawab: ( )1 3 lim + = ∞→ nn 0= ( )!n !n n n n 13 3 lim 1 + = + ∞→ ( ) !n !n n n n 3 1 3 lim 1 + = + ∞→ n n n a a 1 lim + ∞→ =ρ 10 <=ρ , maka n n n n nn 3 ! . !)1( 3.3 lim + = ∞→
- 36. Kalkulus2-unpad 36 Contoh 2. ∑ ∞ =1 2 3 n n n 2 3 n a n n= dan ( )2 1 1 1 3 + = + + n a n n sehingga Karena ∑ ∞ =1 2 3 n n n divergen. Jawab: 3= 2 1 3lim + = ∞→ n n n( )2 21 13 3 lim + = + ∞→ n n n n n ( ) 2 2 1 3 1 3 lim n n n n n + = + ∞→ n n n a a 1 lim + ∞→ =ρ 3=ρ maka
- 37. Kalkulus2-unpad 37 Latihan Selidiki kekonvergenandari deret berikut: ∑ ∞ =1 2 !n n n ∑ ∞ = + 1 ! 5 n n n ( )∑ ∞ =1 !2 .8 n n n n ∑ ∞ = + 1 ! 4 n n n n ( )∑ ∞ =1 3 !2n n n 2. 5. 6. 3. 1. ∑ ∞ =1 !2 .7 n n n n n ∑ ∞ =1 ! n n n n 4. ∑ ∞ =1 4 ! n n n
- 38. Kalkulus2-unpad 38 Uji DeretPositif 6. Uji Akar ∑ ∞ =1n naDiketahui merupakan suatu deret dengan 1. Jika a <1, maka deret konvergen suku-suku yang positif, misalkan 2. Jika a > 1, maka deret divergen 3. Jika a = 1, maka uji tidak memberi kesimpulan. n n n aa ∞→ = lim
- 39. Kalkulus2-unpad 39 Contoh Selidiki kekonvergenanderet 1. ∑ ∞ = − + 1 1 22 n n n n Jawab: n n n n a − + = 1 22 , maka nn n n n n n n aa /1 1 22 limlim − + == ∞→∞→ Karena a=2, maka deret ∑ ∞ = − + 1 1 22 n n n n divergen. .2 1 22 lim = − + = ∞→ n n n
- 40. Kalkulus2-unpad 40 2. ∑ ∞ = − + 112 2 n n n n Jawab: n n n n a − + = 12 2 , maka nn n n n n n n aa /1 12 2 limlim − + == ∞→∞→ Karena a = ½ , maka deret ∑ ∞ = − + 1 1 22 n n n n konvergen. . 2 1 12 2 lim = − + = ∞→ n n n
- 41. Kalkulus2-unpad 41 Latihan Selidiki kekonvergenandari deret berikut: ∑ ∞ = 1 ln 1 n n n ∑ ∞ = − + 1 12 23 n n n n ∑ ∞ = +1 23n n n n ∑ ∞ = + 1 1 2 1 n n n 2. 4. 3.1.
- 42. Kalkulus2-unpad 42 Kesimpulan Untuk mengujikekonvergenan deret ∑ na perhatikan ;na 1. Jika 2. Jika an memuat bentuk ∑⇒≠ ∞→ nn n aa 0lim divergen. nn nrn ,,! , gunakan uji hasil bagi. 3. Jika an hanya memuat bentuk pangkat n yang konstan, gunakan uji banding limit. 4. Usaha terakhir, cobakan uji banding biasa, uji akar, atau uji integral.
- 43. Latihan ∑ ∞ = −3 2 5 1 .1 n n Periksakekonvergenan dari deret berikut : ∑ ∞ = +1 2 5 .2 n n n ( )∑ ∞ = −3 2 2 1 .4 n n ∑ ∞ =1 ! 5 .3 n n n ∑ ∞ = + 1 2 2 2 3 .5 n n nn e ee ∑ ∞ =2 ln .6 n n n ∑ ∞ =1 ! .7 n n n n
- 44. Kalkulus2-unpad 44 Deret GantiTanda (DGT) dan Kekonvergenan Mutlak ( ) ...1 4321 1 1 +−+−=−∑ ∞ = + aaaaa n n n dengan an > 0, untuk semua n. Contoh : deret harmonik berganti tanda, ( ) ... 4 1 3 1 2 1 1 n 1 1 1n 1n +−+−=−∑ ∞ = + Bentuk umum : Deret Ganti Tanda
- 45. Kalkulus2-unpad 45 Uji DeretGanti Tanda Deret ganti tanda dikatakan konvergen jika 0lim.2 = ∞→ n n a ,.1 1+n n a a 1. an monoton turun Pengujian apakah an monoton turun dapat dilakukan 2. Tentukan salah satu dari cara berikut : jika ,1 1 > +n n a a maka an turun. ),(' xf jika .turun0)(' naxf →<
- 46. Kalkulus2-unpad 46 n an 1 = 1 1 1 + =+ n an a. Karena1 1 1 1 1 1 1 1 >+= + = + = + nn n n n a a n n 0 1 limlim. == ∞→∞→ n ab n n n Karena kedua syarat terpenuhi maka deret tersebut konvergen. Jawab : dan maka nn aa <+1 1. Periksa kekonvergenan deret ganti tanda ... 4 1 3 1 2 1 1 +−+− Contoh atau an turun.
- 47. Kalkulus2-unpad 47 Dari soalini kita punya ! 1 n an = , dan ( )!1 1 1 + =+ n an a. ( ) 11 !1 1 ! 1 1 >+= + = + n n n a a n n an >an+1 (an turun). b. 0 ! 1 limlim == ∞→∞→ n a n n n Karena kedua syarat terpenuhi, maka deret konvergen. ... !4 1 !3 1 !2 1 1.2 +−+−
- 48. Kalkulus2-unpad 48 Latihan Selidiki kekonvergenandari deret ganti tanda berikut: ( )∑ ∞ = + + − 1 1 13 2 1 n n n ( )∑ ∞ = − 1 3 1 n n n n ( )∑ ∞ = + + − 1 2 3 1 n n nn n ( )∑ ∞ = + − 1 1 ! 1 n n n n n ( )∑ ∞ = + − 1 )1( 1 1 n n nn 2. 4. 5. 3. 1. ∑ ∞ = + − 1 1 ln )1( n n n n 6.
- 49. Kalkulus2-unpad 49 Konvergen Mutlakdan Konvergen Bersyarat ∑ ∞ =1n nU ∑ ∞ =1n nU ∑ ∞ =1n nU konvergen, maka ∑ ∞ =1n nU konvergen, maka ∑ ∞ =1n nU Misalkan deret dengan suku-suku tak nol, (i) konvergen mutlak. (ii) disebut konvergen bersyarat. ∑ ∞ =1n nUdivergen, tapi Jika Jika
- 50. Kalkulus2-unpad 50 Pengujian Kekonvergenan Mutlak ∑ ∞ =1 || n nU Karena∑ ∞ =1n nU semua sukunya positif, maka gunakan Uji deret positif. Langkah pengujian : Uji Konv deret konvergen mutlak Div Uji ∑ nU Konv deret konvergen bersyarat Div deret divergen (dgn DGT) (uji deret pos)
- 51. Kalkulus2-unpad 51 Contoh 1. ()∑ ∞ = + − 1 1 ! 2 1 n n n n Jawab: n n n n n 2 ! )!1( 2 lim 1 + = + ∞→ 1 2 lim + = ∞→ nn Dari soal diatas kita punya ( ) ! 2 1 1 n U n n n + −= , dan ( )! 2 || n U n n = Menurut uji hasilbagi, Sehingga dengan uji hasil bagi, 0= n n n U U 1 lim + ∞→ =ρ ∑ ∞ =1n nU konvergen, maka ( )∑ ∞ = + − 1 1 ! 2 1 n n n n konvergen mutlak. Selidiki, apakah deret konvergen mutlak, bersyarat atau divergen.
- 52. Kalkulus2-unpad 52 2. ()∑ ∞ = + − 1 1 1 1 n n n Jawab: ( )∑ ∞ = + − 1 1 1 1 n n n Selanjutnya uji ( )∑ ∞ = + − 1 1 1 1 n n n ∑ ∑ ∞ = ∞ = = 1 1 1 n n n n U konvergen bersyarat. divergen dengan uji deret-p. (i) turun.na→ (ii) 0 1 limlim == ∞→∞→ n a n n n dari (i) dan (ii) DGT konvergen atau 1 1 1 11 1/1 /1 1 >+= + = + = + = + nn n n n n n a a n n dengan uji DGT Karena ∑ ∞ =1n nU divergen, tapi ∑ ∞ =1n nU ∑ ∞ =1n nU konvergen. konvergen, maka
- 53. Kalkulus2-unpad 53 Latihan ( )∑ ∞ = − 15 1 n n n n ∑ ∞ = − 1 2 )4( n n n ∑ ∞ = + − 1 23 )1( n n n ( ) ( )∑ ∞ = + − 1 1 1 1 n n nn ∑ ∞ = + − 2 1 ln )1( n n nn ∑ ∞ = + + − 1 1 1 )1( n n nn 1. 2. 3. 5. 6. 7. Selidiki apakah deret berikut konvergen mutlak, konvergen bersyarat atau divergen: ∑ ∞ = − 2 ln )1(.8 n n n n ∑ ∞ = − 1 )1( .4 n nn n e
- 54. Kalkulus2-unpad 54 Deret Pangkat/ Deret Kuasa 2. Deret kuasa dalam (x – b) (pusat x = b) Selanjutnya kita akan mencari himpunan konvergenan(HK). Bentuk Umum deret kuasa: 1. Deret kuasa dalam x (pusat x = 0) ∑ ∞ = ++++= 0 3 3 2 210 ... n n n xaxaxaaxa ∑ ∞ = +−+−+−+=− 0 3 3 2 210 ...)()()()( n n n bxabxabxaabxa Yaitu himpunan semua bilangan real x sehingga deret kuasa konvergen.
- 55. Kalkulus2-unpad 55 Himpunan Kekonvergenan(HK) Misalkan ∑∑ ∞ = ∞ = = 00 n n n n n Uxa dan 1. Jika , maka deret konvergen mutlak. 2. Jika , maka deret divergen 3. Jika , tidak dapat diambil kesimpulan sebelumnya. n n n U U 1 lim + ∞→ =ρ 1<ρ 1=ρ 1ρ >
- 56. Kalkulus2-unpad 56 Soal ∑ ∞ = +02)1(n n n n x ∑ ∞ =0 !n n n x ∑ ∞ =0 ! n n nx 1. 2. 3. ∑ ∞ = + + 0 1 2 )1( .4 n n n x Tentukan Himpunan kekonvergenan dari
- 57. 57 Jawab : Kita akangunakan Uji Hasilbagi Mutlak, untuk menyelidiki kekonvergenan mutlak. Deret tersebut konvergen mutlak apabila , yaitu Kemudian akan kita cek untuk titik ujung intervalnya yaitu x = 2 dan x = -2 . n n n n n n x n x 2)1( : )2(2 lim 1 1 ++ = + + ∞→ 2 x = )2( )1( 2 lim + + = ∞→ n nx n ( ) ( )∑∑ ∞ = ∞ = + = + 11 1 1 21 2 nn n n nn deret ini divergen dengan uji banding limit, maka n n n U U 1 lim + ∞→ =ρ 1<ρ 221 2 <<−⇔< x x Untuk x = 2 HK∉2 ∑ ∞ = +0 2)1( .1 n n n n x Kalkulus2-unpad
- 58. Kalkulus2-unpad 58 Untukx = –2 Sehingga selang kekonvergenannya adalah [-2,2). Ini DGT, maka diuji dengan uji DGT: ( ) ( ) ( ) ( )∑∑ ∞ = ∞ = + − = + − 11 1 1 21 2 n n n n n nn (i) an monoton turun (ii) 0 1 1 limlim = + = ∞→∞→ n a n n n 1 1 1 1 1 2 2/1 1/1 1 > + += + + = + + = + nn n n n a a n n Dari (i) dan (ii) disimpulkan DGT konvergen, HK∈− 2
- 59. Kalkulus2-unpad 59 Jawab : Karena, maka deret selalu konvergen untuk semua nilai x. Gunanakan Uji Hasilbagi Mutlak ; ( ) ! : !1 lim 1 n x n x nn n + = + ∞→ ( )1 lim + = ∞→ n x n Jadi selang kekonvergenannya adalah (-∞,∞)=R. ∑ ∞ =0 ! .2 n n n x n n n U U 1 lim + ∞→ =ρ 1 1 lim|| + = ∞→ n x n 0= 10 <=ρ
- 60. Kalkulus2-unpad 60 Jawab: Gunakan UjiHasilbagi Mutlak ; Jadi deret tersebut konvergen hanya untuk x = 0. ! )!1( lim 1 nx nx n n n + = + ∞→ ( ) xn n 1lim += ∞→ ≠∞ = = 0, 0,0 xjika xjika ∑ ∞ =0 !.3 n n nx n n n U U 1 lim + ∞→ =ρ )1(lim|| += ∞→ nx n Sehingga HK={0}.
- 61. Kalkulus2-unpad 61 Jawab :∑ ∞ = + + 0 1 2 )1( .4 n n n x n n n U U 1 lim + ∞→ =ρ 11 2 )1( 2 . 2 )1( lim ++ + ∞→ + + = n n n n n x x 2 )1( lim + = ∞→ x n 2 1+ = x * Deret konvergen jika 132121 2 1 <<−⇔<+<−⇔< + xx x * Uji x=-3 ∑∑∑ ∞ = + ∞ = ++∞ = + −= − = − 0 1 0 11 0 1 2.)1( 2 2)1( 2 )2( n n n n nn n n n Ini DGT, 02lim ≠= ∞→ n n a jadi DGT divergen. * Untuk x = 1 .2 2 )2( 00 1 ∑∑ ∞ = ∞ = + = nn n n Deret ini divergen dengan uji kedivergenan suku ke-n. Jadi HK = (-3,1). Gunakan uji hasil bagi mutlak;
- 62. Kalkulus2-unpad 62 Teorema 1 Himpunankekonvergenan deret kuasa ∑ ∞ =0n n n xa selang yang berupa salah satu dari ketiga jenis berikut: 1. satu titik x = 0 (jari-jari ; r = 0) 2. selang (-c, c), mungkin ditambah salah satu atau kedua titik ujungnya. (jari-jari ; r = c) 3. seluruh himpunan bilangan real ( jari-jari ; r = ) berbentuk ∞
- 63. Kalkulus2-unpad 63 Teorema 2 Himpunankekonvergenan deret kuasa ∑ ∞ = − 0 )( n n n bxa berbentuk selang yang berupa salah satu dari ketiga jenis berikut : 1. satu titik x = b (jari-jari; r = 0) 2. selang (b-c, c+b), mungkin ditambah salah satu atau kedua titik ujungnya (jari-jari; r = c) 3. seluruh himpunan bilangan real (jari-jari; r = )∞ Dari contoh sebelumnya; 1. HK=[-2,2); r = 2; pusat x = 0 2. HK=R ; r = ; pusat x = 0 3. HK={0} ; r = 0 ; pusat x = 0 4. HK=(-3,1) ; r = 2 ; pusat x =-1 ∞
- 64. Kalkulus2-unpad 64 Latihan Tentukan selangkekonvergenan deret pangkat berikut: ( )∑ ∞ = + − 0 2 1 )1( .1 n n n x ( ) ( ) ( ) ... !3 2 !2 2 2.7 32 + + + + ++ xx x ( )∑ ∞ = + + 0 31 )2( .2 n n n n x ∑ ∞ = − 1 2 )1( .3 n n nn n x ∑ ∞ = − 0 2 4 )1( .4 n n n x ∑ ∞ = +− 1 2 )12()2( .5 n nn n x ( )∑ ∞ = + + − − 1 1 1 )2( )1(.6 n n n n x ( ) ( ) ... 27.3 3ln)2( 9.2 2ln2 3 1ln2 .8 32 + + + + + + xxx
- 65. Kalkulus2-unpad 65 Operasi padaDeret Kuasa ∑ ∞ = = 0 )( n n n xaxS [ ] ...)()(')( 3 3 2 210 0 ++++== ∑ ∞ = xaxaxaaDxaDxSi x n n nx ∑ ∞ = − = 1 1 n n n xna ∫ x dttSii 0 )()( ∑∫ ∞ = = 0 0 n x n n dtta ∑ ∞ = + + = 0 1 1n nn x n a Misal maka
- 66. Kalkulus2-unpad ( )2 1 1 x− ()2 1 1 1 1 xx Dx − = − = 1 1 − ∞ = ∑= n n xn (i) Perhatikan, ...1 32 0 ++++=∑ ∞ = xxxx n n merupakan deret geometri dengan a = 1 ; r = x, maka 1||; 1 1 0 < − =∑ ∞ = x x x n n (ii) 2 3 0 0 1 1 ... 1 x x dt t t t dt t = + + + + −∫ ∫(iii) 66
- 67. ... 3 1 2 1 )1ln( 32 −+−=+ xxxx ... 4 1 3 1 2 1 )1ln(432 +−−−−=− xxxxx ... 4 1 3 1 2 1 ... 4 1 3 1 2 1 )1ln( 432 0 432 ++++=++++=−− xxxxttttx x 1||; 1 )1()1ln( 1 1 <−=+ ∑ ∞ = + xx n x n n n
- 68. Kalkulus2-unpad 68 (iv)Perhatikan ∑ ∞ =0 !n n n x Deretini konvergen untuk setiap x bilangan real. Misal ... !3!2 1)( 32 ++++= xx xxS ... !3!2 1)(' 32 ++++= xx xxS S(x)=S ’(x) x exS =)( Jadi ∑ ∞ = = 0 !n n x n x e
- 69. Kalkulus2-unpad 69 Latihan x xf + = 1 1 )( x x xf + = 1 )( 2 + − = x x xf 1 1 ln)( ( )2 1 1 )( x xf + = 1. 3. 6.2. 5.f(x)=tan-1 (x) ( )x xf 32 1 )( + =7. 2 1 1 )( x xf + =4. Tuliskan fungsi berikut dalam bentuk deret pangkat xx eexf − +=)(.8 x exf 3 )(.9 =
- 70. Kalkulus2-unpad 70 Deret Taylordan Deret Maclurin ( )∑ ∞ = −= 0 )( ! )( )( n n n bx n bf xf Deret di atas disebut Deret Taylor dengan pusat x = b. Bila b = 0, diperoleh Deret Mac Laurin, yaitu ( )∑ ∞ =0 )( ! )0( n n n x n f ... !2 )()('' !1 )()(' )()( 2 + − + − += bxbfbxbf bfxf Misalkan f(x) dapat diturunkan hingga n kali pada x = b, Maka f(x) dapat dinyatakan sebagai deret kuasa dalam (x-b): ... !2 )0('' )0(')0( 2 +++= x f xff
- 71. Contoh 1. Tentukan deretTaylor untuk 2 1 )( + = x xf dengan pusat 1=x Jawab: 44 33 22 3 6 )1(''' )2( 6 )(''' 3 2 )1('' )2( 2 )('' 3 1 )1(' )2( 1 )(' 3 1 )1( − =→ + − = =→ + = − =→ + − = = f x xf f x xf f x xf f … Sehingga ...)1( !3 )1(''' )1( !2 )1('' )1( !1 )1(' )1()( 32 +−+−+−+= x f x f x f fxf
- 72. ...)1( !33 6 )1( !23 2 )1( !13 1 3 1 )( 3 4 2 32 +−−−+−−= xxxxf n n n n x)1( 3 1 )1( 0 1 −−= ∑ ∞ = +
- 73. Kalkulus2-unpad 73 f(x) =sin x f ’(x) = cos x f ’’(x) = - sin x f’’(0) = 0 f’(0) = 1 f(0) = 0 f ’’’(x) = - cos x f’’’(0) = -1 f lV (x) = sin x f lV (0) = 0 Sehingga, ... !7!5!3 sin)( 753 +−+−== xxx xxxf ( ) ( )∑ ∞ = + + −= 0 12 !12 1 n n n n x 2. Tentukan deret MacLaurin untuk xxf sin)( =
- 74. Kalkulus2-unpad 74 f(x) =ex f ’(x) = ex f ’’(x) = ex f’’(1) = e1 f’(1) = e1 f(1) = e1 f ’’’(x) = ex f’’’(1) = e1 f lV (x) = ex f lV (1) = e1 Sehingga, ... !4 )1( !3 )1( !2 )1( )1()( 432 + − + − + − +−+== x e x e x exeeexf x ∑ ∞ = − = 0 ! )1( n n n xe x exf =)(3. Tentukan deret Taylor dari dengan pusat x = 1.
- 75. Kalkulus2-unpad 75 Atau, kitadapat menggunakan operasi deret, 11+− = xx ee 1 . − = x ee ∑ ∞ = − = 0 ! )1( n n n x e ∑ ∞ = − = 0 ! )1( n n n xe
- 76. Kalkulus2-unpad 76 Latihan 1. Perderetkanf(x) berikut dalam deret Maclaurin a. f(x) = cos x b. f(x) = ln(3+2x) a. f(x) = ex , a = 2 c. f(x) = tan x 2. Perderetkan f(x) berikut dalam deret taylor dengan pusat x = a 1 1 )(. + = x xfd 1, 5 1 )(. = + = a x xfb 3, 1 )(. == a x xfc