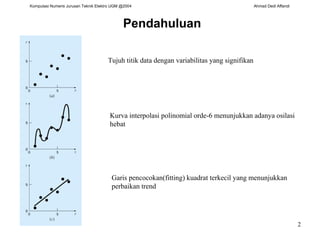
Bab membahas berbagai metode regresi untuk memodelkan hubungan antara variabel bebas dan terikat, termasuk regresi linier, polinomial, dan nonlinier. Metode utama yang digunakan adalah kuadrat terkecil untuk mengestimasi parameter model sedemikian rupa sehingga dapat meminimalkan galat perkiraan.

1. Bab 11 Regresi Kuadrat Terkecil

2. Pendahuluan Tujuh titik data dengan variabilitas yang signifikan Kurva interpolasi polinomial orde-6 menunjukkan adanya osilasi hebat Garis pencocokan(fitting) kuadrat terkecil yang menunjukkan perbaikan trend

3. Regresi Linear Diketahui : n titik ( x 1 , y 1 ), ( x 2 , y 2 ), …, ( x n , y n ) Ditanya : Garis y = a 0 + a 1 x yang paling sesuai dengan n titik diatas . minimize minimize minimize minimize

4. Pencocokan Kuadrat Terkecil sebuah Garis Untuk me minimize S r : dengan dan

5. Contoh Pencocokan Kuadrat Terkecil sebuah Garis

6. Error Kuantifikasi Pada Regresi Linear S kecil r S besar r Keduanya dapat di-dekati dengan baik (coefficient of determination) ( Koefisien korelasi )

7. Contoh Apli k a s i Regresi Linear (a) (b) Seberapa baik perkiraannya Eq. (a) Eq. (b) Measured v Calculated v by Eq. (a) Calculated v by Eq. (b) Pencocokkan yang baik akan punya lereng 1,intercept 0 dan r 2 = 1. v model = -0.859 + 1.032 v measure v model = 5.776 + 0.752 v measure

8. Lineari s a s i Persamaan Nonlinear Regresi Nonlinear Transformasi Linear ( jika mungkin ) Data yang tidak cocok dengan bentuk linear

10. Regresi Polinomial Diketahui : n titik ( x 1 , y 1 ), ( x 2 , y 2 ), …, ( x n , y n ) Ditanya : Suatu polinomial y = a 0 + a 1 x + a 2 x 2 + … a m x m yang me minimizes Contoh : polynomial 2 nd -order y = a 0 + a 1 x + a 2 x 2 Standard error:

11. Contoh regresi Polinomial 2 nd -order m = 2 ∑ x i = 15 ∑ x i 4 = 979 n = 2 ∑ y i = 152.6 ∑ x i y i = 585.6 ∑ x i 2 = 55 ∑ x i 2 y i = 2488.9 ∑ x i 3 = 225 y = 2.47857 + 2.35929x + 1.86071x 2

12. Regresi Linear Jamak Diketahui : n titik 3D ( y 1 , x 11 , x 12 ) ( y 2 , x 12 , x 22 ), …, ( y n , x 1n , x 2n ) Ditanya : suatu bidang y = a 0 + a 1 x 1 + a 2 x 2 yg me minimizes Pembuatan sampai ke dimensi ke- m : hyper plane y = a 0 + a 1 x 1 + a 2 x 2 + … + a m x m

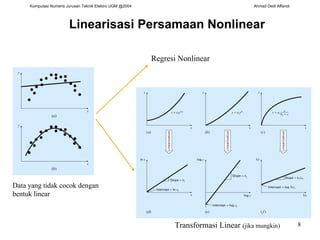
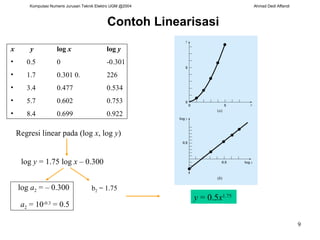
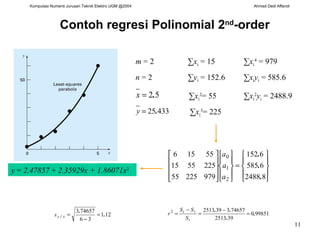
13. Kuadrat Terkecil Linear secara Umum Kuadrat Terkecil Linear : y = a 0 + a 1 x 1 Kuadrat Terkecil Multi linear : y = a 0 + a 1 x 1 + a 2 x 2 + … + a m x m Kuadrat Terkecil polinomial : y = a 0 + a 1 x + a 2 x 2 + … a m x m y = a 0 z 0 + a 1 z 1 + a 2 z 2 + … + a m z m {Y} = [Z] {A} + {E} [C] {A} = {D} ([C] simetris , misal . linear dan polynomial)

14. Regresi Non Linear Misal Kita tahu bahwa data {( x 1 , y 1 ), ( x 2 , y 2 ), …, ( x n , y n )} mirip dengan fungsi f ( x ) = a 0 (1 – e - a 1 x ); bagaimana cara mencari a 0 d an a 1 yang paling tepat ? Ekspansi deret Taylor + regresi linear + itera si {D} = [Z j ] { ∆A} + {E} a 0,j+1 = a 0,j + ∆ a 0 and a 1,j+1 = a 1,j + ∆ a 1 Ekspansi t aylor pada titik data x i and state sakarang j Least squares