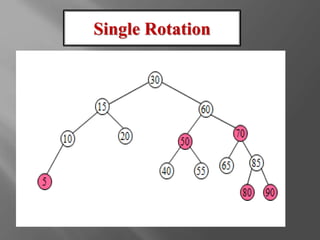
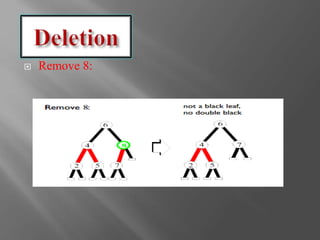
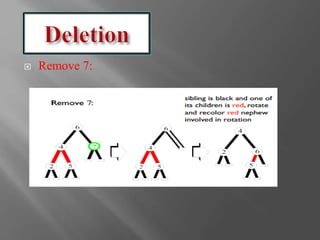
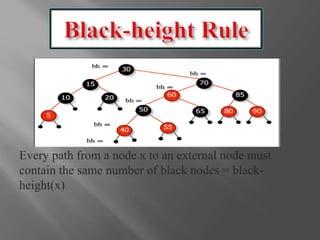
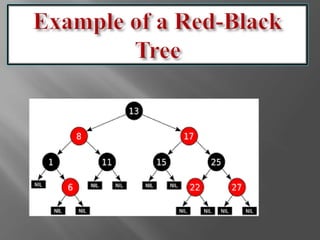
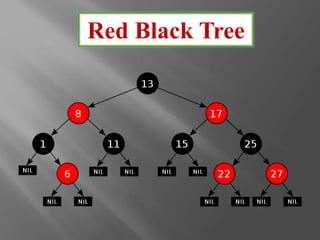
The document discusses red-black trees, which are a type of self-balancing binary search tree. Red-black trees were invented in 1972 by Rudolf Bayer as a way to maintain the balancing of binary search trees during insertion and deletion operations. They support common binary search tree operations like search, insert, and delete in O(log n) time on average and worst case. The document outlines the properties and balancing operations used to maintain a red-black tree during insertions and deletions.

1. Submitted to:
Miss.Komal Bashir
Submitted by:
Maira shahnawaz
Uneza rehman
Amna siddiqui

2. Binary Search Tree (BST) is a good
data structure and It supports:
 Insertion
 Deletion
 Search

3.  Red-Black Tree is one of the balanced binary search
tree
 A red-black tree is a binary search tree with one
extra attribute for each node: the colour, which is
either red or black

4. Invented 1972
Invented by Rudolf Bayer
Time complexity in big (o) notation:
Average Worst case
Space O(n) O(n)
Search O(log n) O(log n)
Insert O(log n) O(log n)
Delete O(log n) O(log n)

5. That's really your decision, but I've found that red black
trees are best suited to largely random data that has
occasional degenerate runs, and searches have no
locality of reference. This takes full advantage of the
minimal work that red black trees perform to maintain
balance compared to AVL trees and still allows for
speedy searches.

6. A binary search tree is a red-black tree if:
Every node is either red or black
The root is black
Every leaf (NIIL) is black
A red node’s children are black

7. Every path from a node x to an external node must
contain the same number of black nodes = black-
height(x)

9. Red Black Tree

10. Since red-black tree is a balanced BST, it supports
 Search
 Insertion
 Deletion

11.  A new item is always inserted as a leaf in the tree
 If we color a leaf black, we will create a longer path
of black nodes (violating property 4)
 Therefore, a new item must be colored red [unless it
is the root]
 if the parent is colored black, we are done

12.  If the parent is red, we will have consecutive red
nodes (violating property 3)
 We must adjust the tree to ensure property three,
without introducing a violation to property 4
 The operations are rotations and color changes.

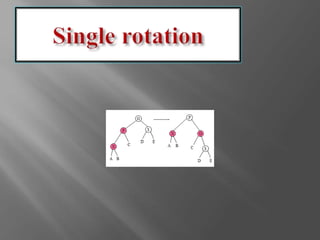
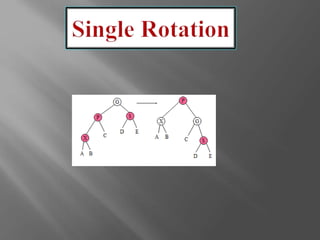
13.  Sibling of the parent is black [adopt the convention
that null references are black]
 Inserted node is an outside grandchild
 A single rotation between the parent and the
grandparent, with appropriate color changes,
restores property 3

15.  Notice that before insertion of node X, there was
one black node from G to each of A, B, and C, and
two black nodes from G to each of D and E
 After the rotation and recoloring, notice that the
number of black nodes on each of those paths
remains unchanged
 Property 3 has been restored

16.  Sibling of the parent is red
 Neither single nor double rotations work, since both
result in (possibly) consecutive red nodes
Case 2

18.  This fixes property 3 for this sub tree
 What happens if the parent of this sub tree is also
red?
 We could percolate this procedure up toward the
root until we no longer have two consecutive re
nodes, or we reach the root
 The advantage over AVL trees has disappeared

20. Color flip

21. Single Rotation

22.  Recall that in deleting from a binary search tree, the
only nodes which are actually removed are leaves or
nodes with exactly one child
 Nodes with two children are never removed. Their
contents are just replaced
Deletions

23.  If the node to be deleted is red, there is no problem -
- just delete the node
 If the node to be deleted is black, its removal will
violate property 4
 The solution is to ensure that any node to be deleted
is red

24.  Remove 9

25.  Remove 8:

26.  Remove 7:

27. Although you may never need to implement your own
set or map classes, thanks to their common built-in
support, understanding how these data structures work
should help you better assess the performance of your
applications and give you more insight into what
structure is right for a given task. For more practice with
these concepts, check out these problems from the Top
Coder archive that involve trees: