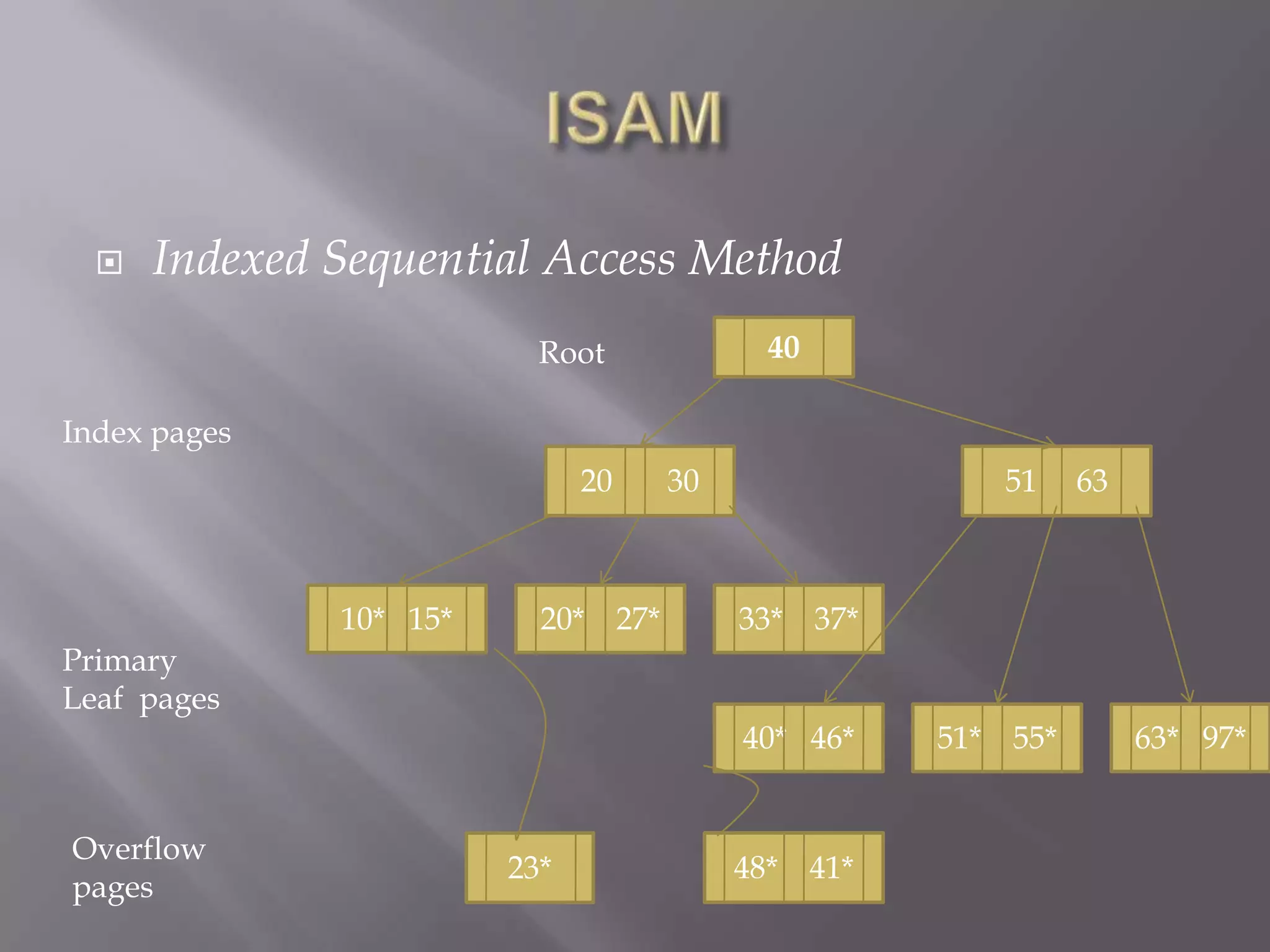
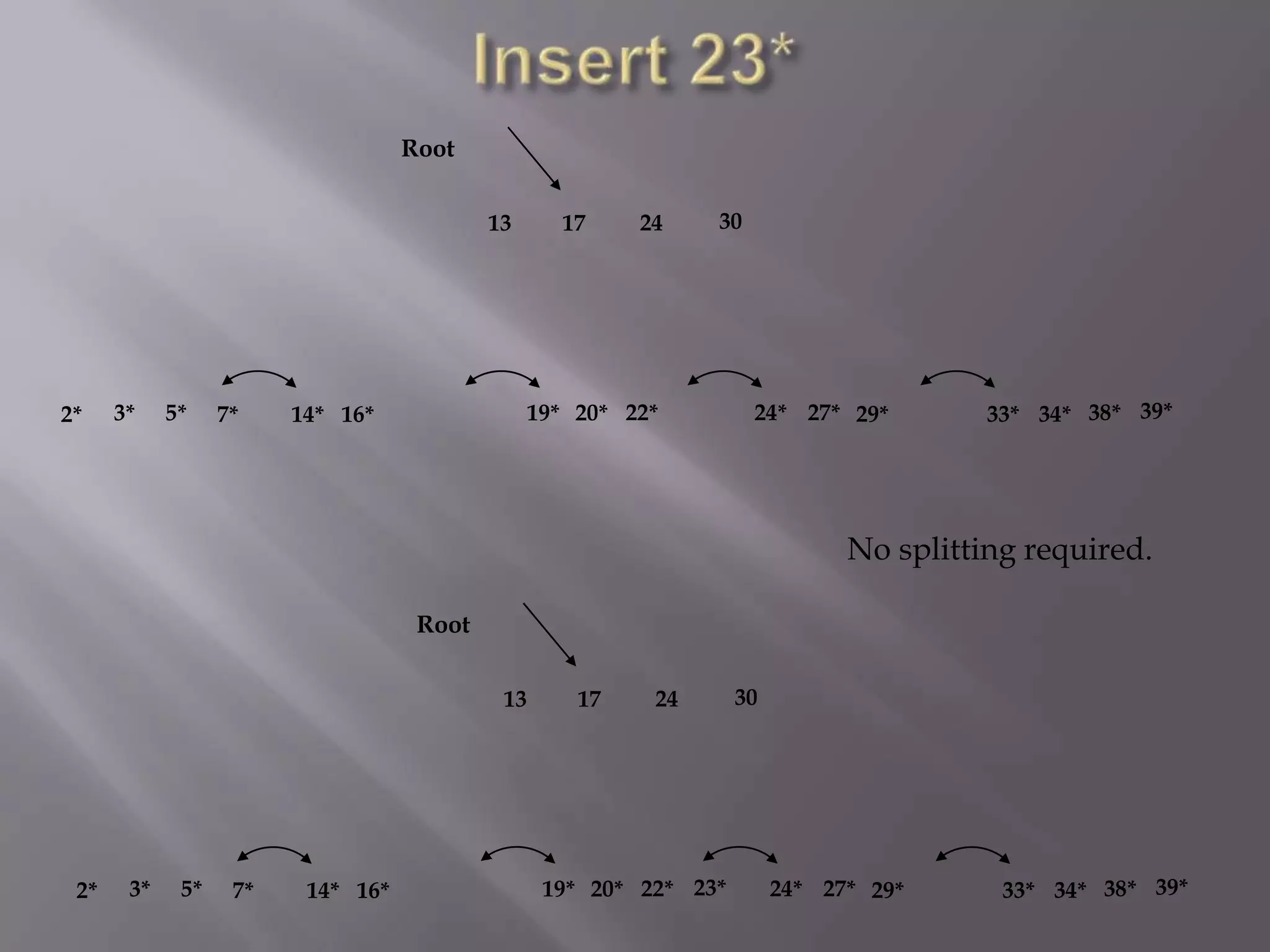
The document discusses B+ trees, which are self-balancing search trees used to index large blocks of data. It describes the basic structure of B+ trees, including leaf nodes containing data entries and non-leaf nodes containing index entries that point to child nodes. It also covers common operations like searching, insertion, and deletion in B+ trees and how these operations may involve splitting or merging nodes to maintain the tree's balance.

1. By:
ANITHA RANI.K.S(1MS10IS014)

2.  The Trees where the minimal separator is not
considered as the element for index.
 B+ Tree is characterized by its order.
 Consists of a sequence set and an index set.

3.  Indexed Sequential Access Method
Root 40
Index pages
20 30 51 63
10* 15* 20* 27* 33* 37*
Primary
Leaf pages
40* 46* 51* 55* 63* 97*
Overflow
23* 48* 41*
pages

4. • Index entries:<search key value, page id> they
direct search for data entries in leaves.
• Example where each node can hold 2 entries;
Root
40
20 30 51 63
10* 15* 20* 27* 33* 37* 40* 46* 51* 55* 63* 97*

5. • Balanced
• Every node except root must be at least ½ full.
• Order: the minimum number of keys/pointers in
a non-leaf node
• Fanout of a node: the number of pointers out of
the node

6. • Typical order: 100. Typical fill-factor: 67%.
– average fanout = 133
• Typical capacities:
– Height 3: 1333 = 2,352,637 entries
– Height 4: 1334 = 312,900,700 entries
• Can often hold top levels in buffer pool:
– Level 1 = 1 page = 8 Kbytes
– Level 2 = 133 pages = 1 Mbyte
– Level 3 = 17,689 pages = 133 MBytes

7. • Search begins at root, and key comparisons direct it to a
leaf.
• Search for 5*, 15*, all data entries >= 24* ...
Root
13 17 24 30
2* 3* 5* 7* 14* 16* 19* 20* 22* 24* 27* 29* 33* 34* 38* 39*
Based on the search for 15*, we know it is not in the tree!

8. • Searching:
– logd(n) – Where d is the order, and n is the number of entries
• Insertion:
– Find the leaf to insert into
– If full, split the node, and adjust index accordingly
– Similar cost as searching
• Deletion
– Find the leaf node
– Delete
– May not remain half-full; must adjust the index accordingly

9. Root
13 17 24 30
2* 3* 5* 7* 14* 16* 19* 20* 22* 24* 27* 29* 33* 34* 38* 39*
No splitting required.
Root
13 17 24 30
2* 3* 5* 7* 14* 16* 19* 20* 22* 23* 24* 27* 29* 33* 34* 38* 39*

10. Root
Root
17
13 17 24 30
5 13 24 30
2* 3* 5* 7* 14* 16* 19* 20* 22* 24* 27* 29* 33* 34* 38* 39*
2* 3* 5* 7* 8* 14* 16* 19* 20* 22* 24* 27* 29* 33* 34* 38* 39*
 Notice that root was split, leading to increase in height.
 In this example, we can avoid split by re-distributing
entries; however, this is usually not done in practice.

11. Data 2* 3* 5* 7* 8*
Page Entry to be inserted in parent node.
Observe how
…
• (Note that 5 is copied up and
s
Split 5
minimum continues to appear in the leaf.)
occupancy is
guaranteed in both 2* 3* 5* 7* 8*
leaf and index pg
splits.
• Note difference Index 5 13 17 24 30
between copy-up Page
Entry to be inserted in parent node.
and push-up; be Split 17 (Note that 17 is pushed up and only
appears once in the index. Contrast
sure you this with a leaf split.)
understand the
reasons for this. 5 13 24 30

12. Delete 19*
Root
17
Root
5 13 24 30
13 17 24 30
2* 3* 5* 7* 8* 14* 16* 19* 20* 22* 24* 27* 29* 33* 34* 38* 39*
2* 3* 5* 7* 14* 16* 19* 20* 22* 24* 27* 29* 33* 34* 38* 39*
Root
17
5 13 24 30
2* 3* 5* 7* 8* 14* 16* 20* 22* 24* 27* 29* 33* 34* 38* 39*

13. Delete 20* ...
Root
17
5 13 24 30
2* 3* 5* 7* 8* 14* 16* 20* 22* 24* 27* 29* 33* 34* 38* 39*
Root
17
5 13 27 30
2* 3* 5* 7* 8* 14* 16* 22* 24* 27* 29* 33* 34* 38* 39*

14. • Deleting 19* is easy.
• Deleting 20* is done with re-distribution. Notice how
middle key is copied up.
• Further deleting 24* results in more drastic changes

15. Delete 24* ...
Root
17
5 13 27 30
2* 3* 5* 7* 8* 14* 16* 22* 24* 27* 29* 33* 34* 38* 39*
Root No redistribution from
17
neighbors possible
5 13 27 30
2* 3* 5* 7* 8* 14* 16* 22* 27* 29* 33* 34* 38* 39*

16. • Must merge.
30
• Observe `toss’ of index entry
(on right), and `pull down’ of
index entry (below).
22* 27* 29* 33* 34* 38* 39*
Root
5 13 17 30
2* 3* 5* 7* 8* 14* 16* 22* 27* 29* 33* 34* 38* 39*

17. • Tree is shown below during deletion of 24*. (What
could be a possible initial tree?)
• In contrast to previous example, can re-distribute
entry from left child of root to right child.
Root
22
5 13 17 20 30
2* 3* 5* 7* 8* 14* 16* 17* 18* 20* 21* 22* 27* 29* 33* 34* 38* 39*

18. • Intuitively, entries are re-distributed by `pushing through’
the splitting entry in the parent node.
• It suffices to re-distribute index entry with key 20; we’ve
re-distributed 17 as well for illustration.
Root
17
5 13 20 22 30
2* 3* 5* 7* 8* 14* 16* 17* 18* 20* 21* 22* 27* 29* 33* 34* 38* 39*