The document discusses red-black trees, which are self-balancing binary search trees. It describes the basic operations on dynamic sets like search, insert, and delete. It then explains the properties and structure of red-black trees, including that they ensure height is O(log n) through coloring nodes red or black. The insert and fixup algorithms are shown to maintain these properties and run in O(log n) time, providing efficient search tree operations.

1. Red-black Trees
Author:
Varun Mahajan
<varunmahajan06@gmail.com>

2. Contents
●
Dynamic sets
●
Operations on Dynamic sets
●
Binary trees: Basic terminology
●
Binary search trees
●
TREE_SEARCH
●
TREE_INSERT
●
Operations' running time: O(h)
●
Red-black trees
●
Red-black properties
●
Height: O(lg n)
●
Queries: O(lg n)
●
Rotations: O(1)
●
RB-INSERT: O(lg n)

3. Dynamic sets
Set: A collection of objects of a particular kind
The Sets manipulated by algorithms can grow, shrink, or otherwise change
over time. Such sets are called Dynamic Sets
In a typical implementation of a dynamic set, each element is represented by
an object whose fields can be examined and manipulated if we have a pointer
to the object
Object fields:
●
Identifying Key field
●
Satellite data

4. Operations on Dynamic sets
Two categories:
●
Queries
●
Modifying Operations
SEARCH(S,k): A query that, given a set S and a key value k, returns a
pointer x to an element in S such that key[x] = k, or NIL if no such element
belongs to S
INSERT(S,x): A modifying operation that augments the set S with the
element pointed to by x. We usually assume that any fields in element x
needed by the set implementation have already been initialized
DELETE(S,x): A modifying operation that, given a pointer x to an element in
the set S, removes x from S. (Note that this operation uses a pointer to an
element x, not a key value.)
MINIMUM(S): A query on a totally ordered set S that returns a pointer to
the element of S with the smallest key

5. Operations on Dynamic sets
MAXIMUM(S): A query on a totally ordered set S that returns a pointer to
the element of S with the largest key
SUCCESSOR(S,x): A query that, given an element x whose key is from a
totally ordered set S, returns a pointer to the next larger element in S, or NIL
if x is the maximum element
PREDESESSOR(S,x): A query that, given an element x whose key is from a
totally ordered set S, returns a pointer to the next smaller element in S, or
NIL if x is the minimum element
Totally ordered set: For any two elements a and b in the set, exactly one of the
following must hold: a < b, a = b, or a > b

6. Binary trees
Binary trees are defined recursively. A binary tree T is a structure defined on
a finite set of nodes that either
●
contains no nodes, or
●
is composed of three disjoint sets of nodes: a root node, a binary tree
called its left subtree, and a binary tree called its right subtree
The binary tree that contains no nodes is called the empty tree or null tree,
sometimes denoted NIL
If the left subtree is nonempty, its root is called the left child of the root of
the entire tree
Likewise, the root of a nonnull right subtree is the right child of the root of
the entire tree
A node with no children is an external node or leaf
A nonleaf node is an internal node

7. Binary trees
If n1, n2, . . . , nk is a sequence of nodes in a tree such that ni is the parent
of ni+1 for 1 ≤ i < k, then this sequence is called a path from node n1 to
node nk.
The length of a path is one less than the number of nodes in the path
The height of a node in a tree is the length of a longest path from the node
to a leaf
The height of a tree is the height of the root
The depth of a node is the length of the unique path from the root to that
node

8. Binary Search trees
The keys in a binary search tree are always stored in such a way as to
satisfy the binary-search-tree property:
●
Let x be a node in a binary search tree. If y is a node in the left subtree
of x, then key[y] ≤ key[x]. If y is a node in the right subtree of x, then
key[x] ≤ key[y]

9. TREE-SEARCH
T R E E -S E A R C H (T, k )
if T = N I L of k = key[T ]
return T
els e if k < key[T ]
return T R E E -S E A R C H (left[T ], k )
els e
return T R E E -S E A R C H (rig ht[T ], k )
TREE-SEARCH runs in O(h) time on a tree of height h
(a) A binary search tree on 6 nodes
with height 2. (b) A less efficient
binary search tree with height 4 that
contains the same keys

10. TREE-INSERT
T R E E -I N S E R T (T, x )
if T = N I L
T = x
return
els e if key[x ] < key[T ]
return T R E E -I N S E R T (left[T ], x )
els e
return T R E E -I N S E R T (rig ht[T ], x )
TREE-INSERT runs in O(h) time on a tree of height h
Inserting an item with key 13 into a binary
search tree. Lightly shaded nodes indicate the
path from the root down to the position where
the item is inserted. The dashed line indicates
the link in the tree that is added to insert the
item

11. Binary Search trees Operations: Running time
The worst-case running time for most search-tree operations is
proportional to the height of the tree
Queries:
●
TREE-SEARCH(S,k): O(h)
●
TREE-MINIMUM(S): O(h)
●
TREE-MAXIMUM(S): O(h)
●
TREE-SUCCESSOR(S,x): O(h)
●
TREE-PREDECESSOR(S,x): O(h)
Modifying operations:
●
TREE-INSERT(S,x): O(h)
●
TREE-DELETE(S,x): O(h)

12. Red-black trees
Red-black trees are binary search trees that are "balanced" in order to
guarantee that basic dynamic-set operations take O(lg n) time in the
worst case (height of the tree: O(lg n) where n is the no of nodes)
A red-black tree is a binary search tree with one extra bit of storage per node:
its color, which can be either RED or BLACK. By constraining the way
nodes can be colored on any path from the root to a leaf, red-black
trees ensure that no such path is more than twice as long as any
other, so that the tree is approximately balanced

13. Red-black properties
Binary search tree is a red-black tree if it satisfies the following red-black
properties:
●
Every node is either red or black
●
The root is black
●
Every leaf (NIL) is black
●
If a node is red, then both its children are black
●
For each node, all paths from the node to descendant leaves contain the same
number of black nodes
The number of black nodes on any path from, but not including, a node x down to a leaf
is called the black-height of the node, denoted as bh(x)
black-height of a red-black tree is the black-height of its root

14. Height O(lg n)
A red-black tree with n internal nodes has height at most 2 lg(n + 1)
i.e. O(lg n)
●
A subtree rooted at x contains internal nodes >= 2^bh(x) -1
●
For leaf: bh(leaf) = 0 => internal nodes = 2^0 - 1 = 0 (TRUE)
●
For internal node x with two children:
●
Each child has black height bh(x) or bh(x) -1, depending on whether its color is red or
black, respectively
●
Subtree rooted at x: internal nodes >= (2^ (bh(x) – 1) -1) + (2^ (bh(x) – 1) -1) + 1 =
2^bh(x) -1 (TRUE)
●
Claim is proved by induction
●
The black-height of the root must be at least h/2 by property 4 (h is
height of tree)
●
n >= 2^bh(root) - 1
●
n >= 2^(h/2) – 1
●
lg(n +1) >= h/2
●
h <= 2 lg(n+1)
An immediate consequence of this lemma is that the dynamic-set operations
SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, and PREDECESSOR can be
implemented in O(lg n) time on red-black trees, since they can be made to run
in O(h) time on a search tree of height h and any red-black tree on n nodes is a
search tree with height O(lg n)

15. Rotations
• A local operation in a
search tree which changes
the pointer structure and
preserves the binary-
search-tree property
• Both LEFT-ROTATE and
RIGHT-ROTATE run in O(1)
time. Only pointers are
changed by a rotation; all
other fields in a node
remain the same

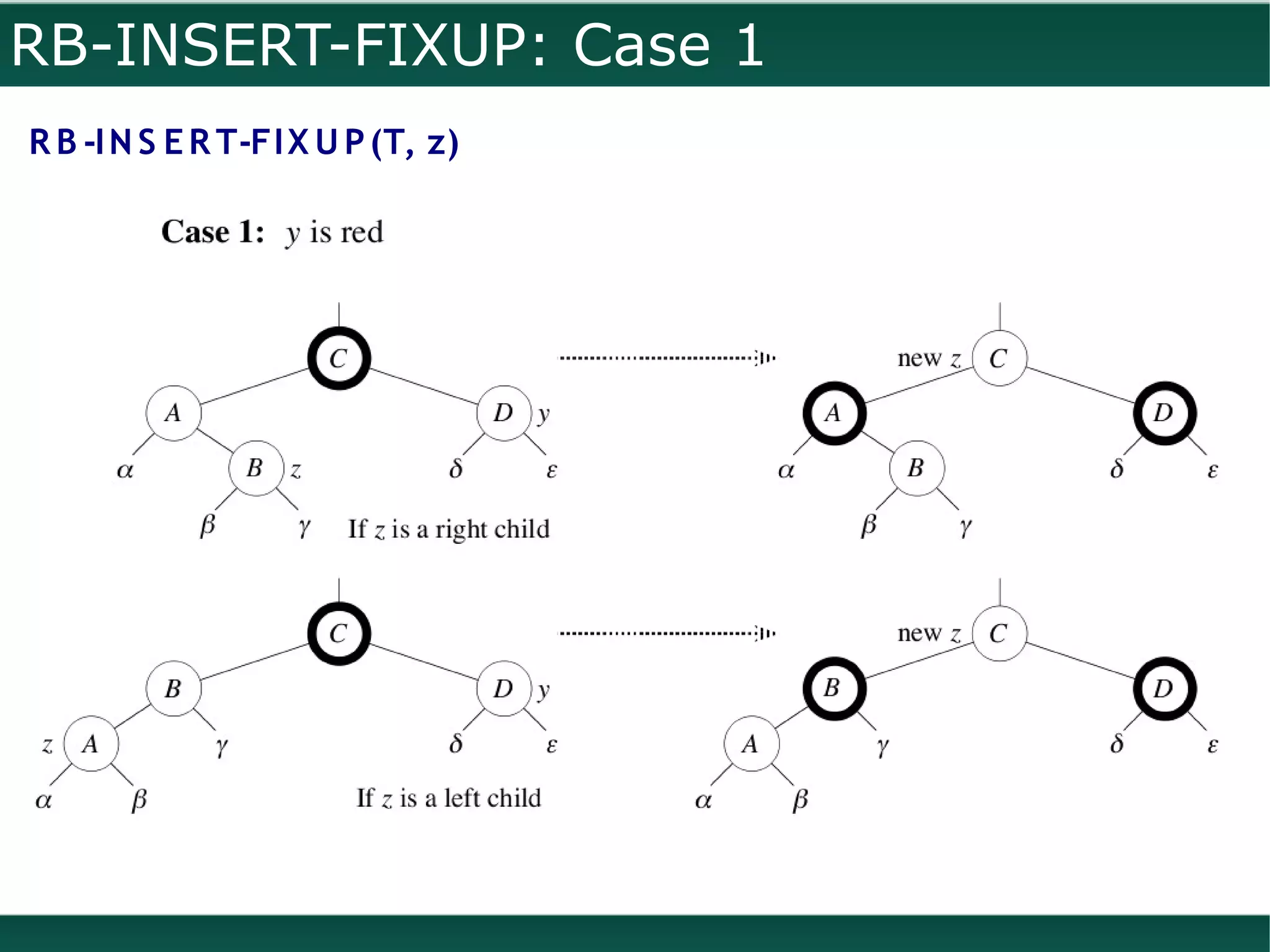
16. RB-INSERT
R B -I N S E R T (T, z)
T R E E -I N S E R T (T, z)
c o lo r[z] = R E D
R B -I N S E R T-FI X U P (T, z)

17. RB-INSERT-FIXUP: Case 1
R B -I N S E R T-FI X U P (T, z)

18. RB-INSERT-FIXUP: Case 2,3
R B -I N S E R T-FI X U P (T, z)

19. RB-INSERT-FIXUP: Example

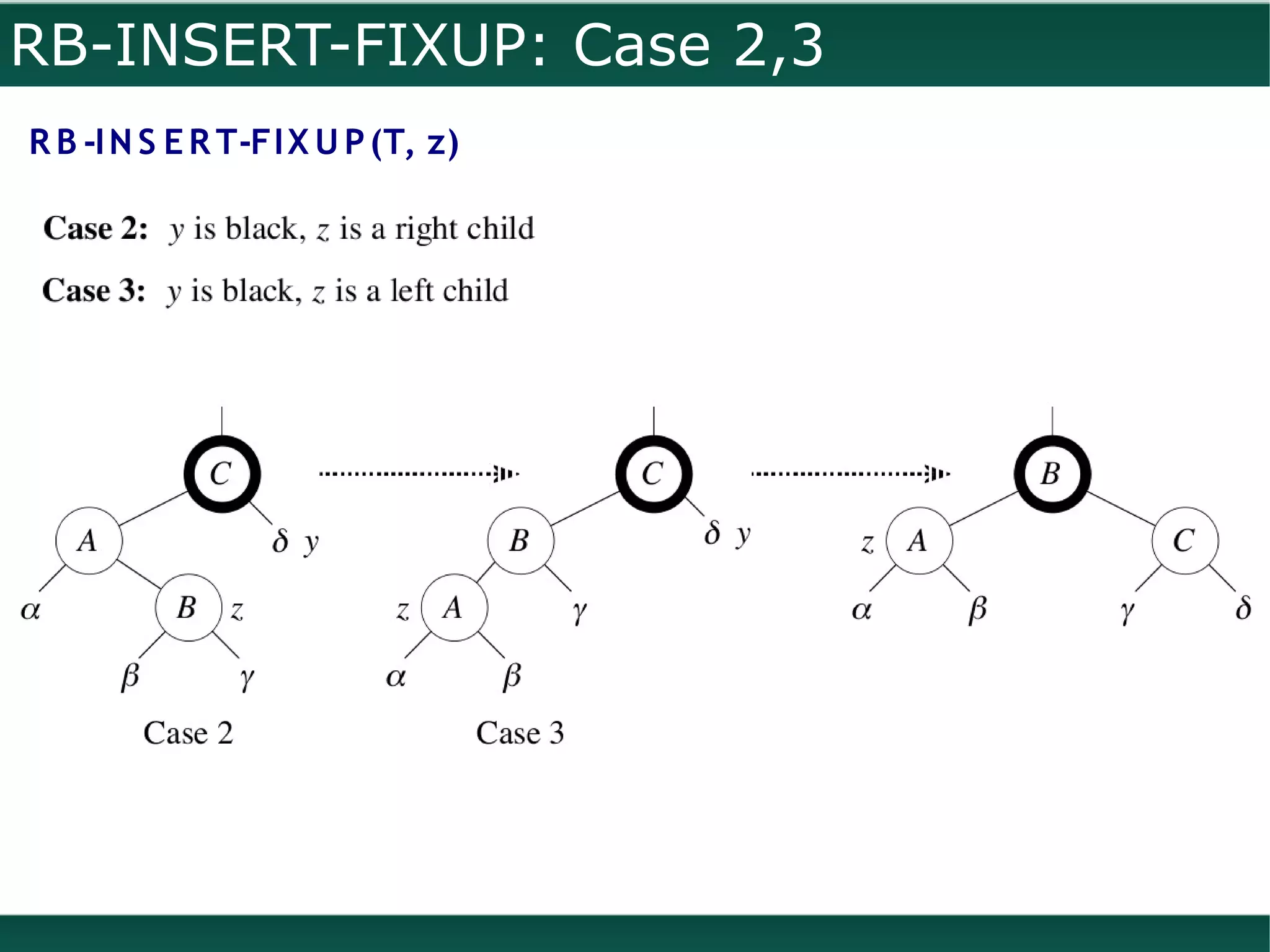
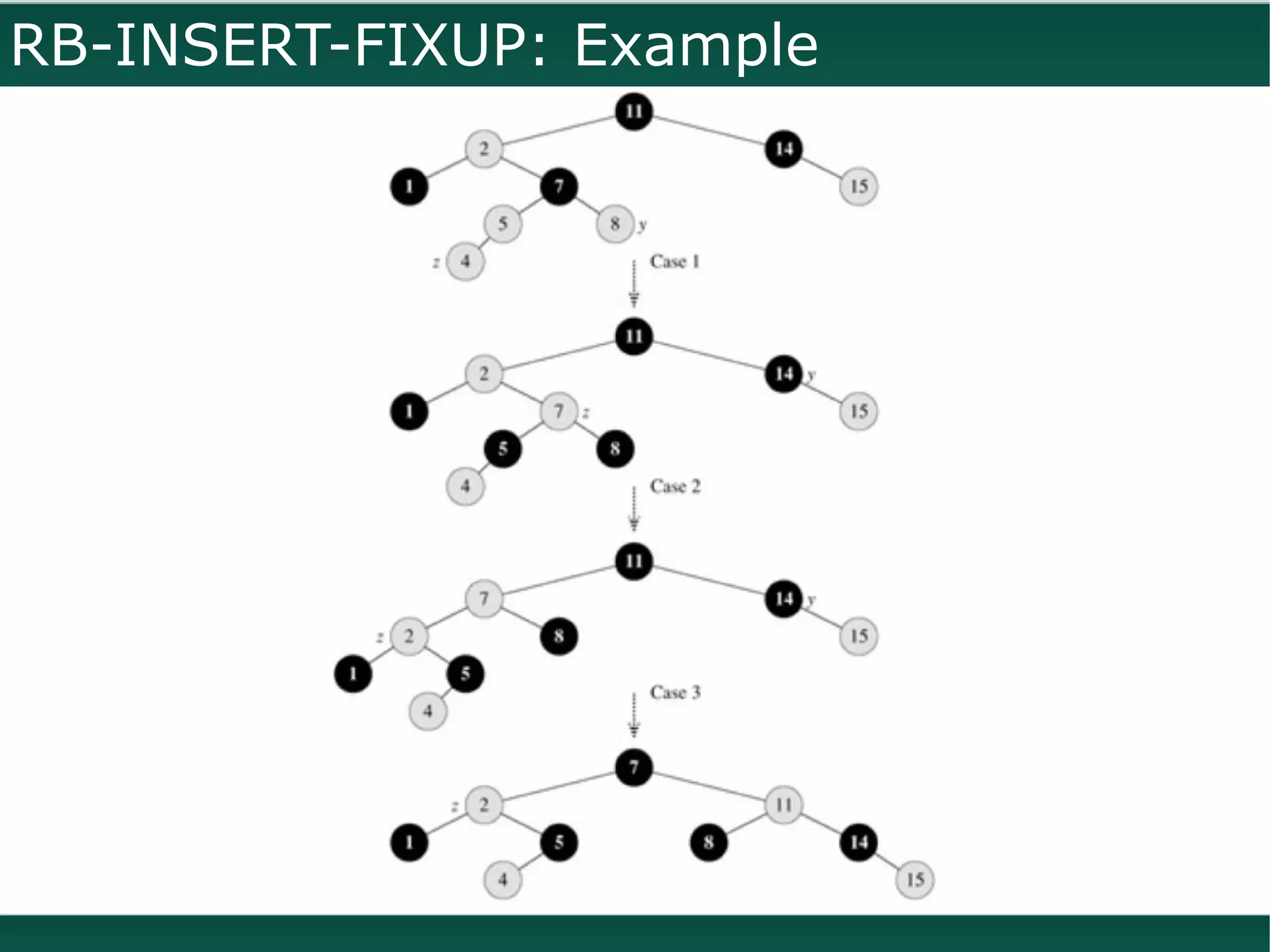
20. RB-INSERT: Running time
R B -I N S E R T (T, z): O (lg n)
T R E E -I N S E R T (T, z) O (lg n)
c o lo r[z] = R E D O (1)
R B -I N S E R T-FI X U P (T, z) O (lg n)
R B -I N S E R T-FI X U P (T, z): O (lg n)
●
Case 1: The pointer z moves two levels up the tree. Maximum times this can happen
(when case 1 is repeated) is O(lg n)
●
Case 2,3: At the maximum two rotations are done
The running time of RB-DELETE(T, z) is also O(lg n)

21. Exercise
Study:
●
TREE-DELETE, TREE-SUCCESSOR, TREE_PREDECESSOR
●
RB-DELETE
●
Linux kernel implementation of Red-black tree:
●
../include/linux/rbtree.h
●
../lib/rbtree.c

22. References
●
Introduction to Algorithms, Second Edition, Thomas H. Cormen, Charles E. Leiserson, Ronald
L. Rivest, Clifford Stein; The MIT Press
●
http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-introduction-to-alg
●
http://lwn.net/Articles/184495/

23. END...