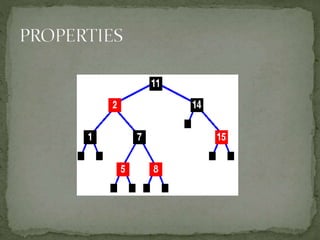
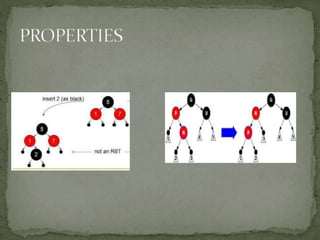
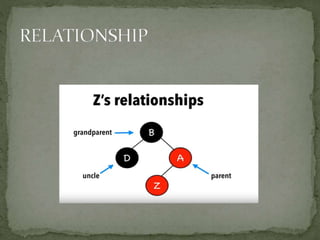
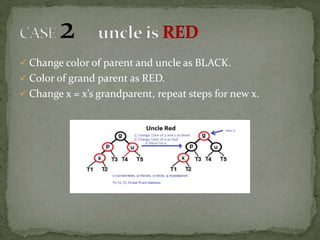
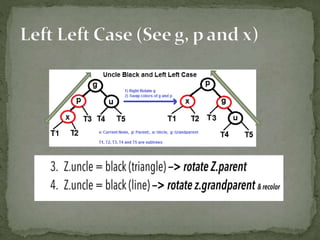
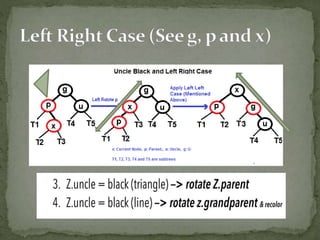
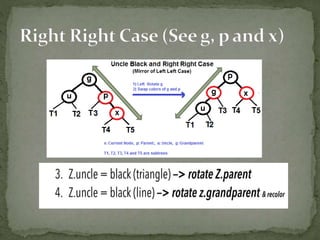
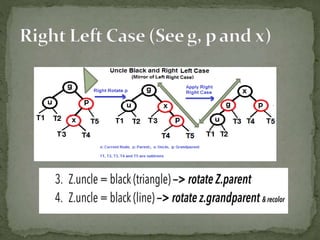
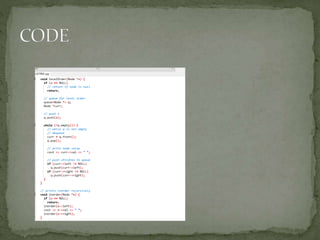
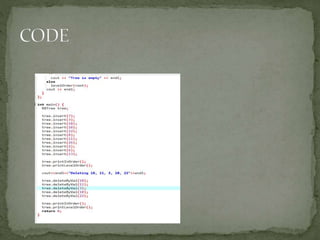
This document discusses red-black trees, which are self-balancing binary search trees. Each node of a red-black tree has an extra bit denoting its color, either red or black. Operations like insertion, lookup, and deletion can be performed in O(log n) time due to rebalancing techniques and restrictions on how nodes are colored. Some examples of using red-black trees include implementing maps and sets in libraries, organizing virtual memory, and CPU scheduling. Code examples and references are provided.

1. DATA STRUCTURE AND ALGORTHM
AYESHA ZAKA

2.  INTRODUCTION
 OPERATIONS
 PROPERTIES
 RELATIONSHIP
 STRATEGY
 INSERTION
 ADVANTAGES
 COMPLEXITY
 APPLICATION
 CODE
 REFRENCES
 ANIMATION (ONLINE)

3.  RED-BLACK TREE
* self-balancing binary search
tree (BST)

4.  RED-BLACK TREE
Each node has an extra bit
*Bit is often interpreted as the color
* Red or Black of the node.
* Root of tree is always black
*Color bits are used to ensure the tree remains
balanced during insertions and deletions.

5.  INSERT
Insert a key value
 LOOKUP
Determine whether a key value is in the tree
 DELETE
Remove key value from the tree
 PRINT
Key values in sorted order (print)

6.  The root node should always black.
 Every null child of a node is black .
 The children of a red node are black. It can be possible that
parent of red node is black node.
 All the leaves have the same black depth.
 Every simple path from the root node to the (downward) leaf
node contains the same number of black nodes.
 Root property
 The root of the red-black tree is black
 Red property
 The children of a red node are black.
 Black property
 Every leaf which is nil is black

12. Tools
1) Recoloring
2) Rotation
 Color of a NULL node is considered as BLACK.
 Let x be the newly inserted node.
*Perform standard BST insertion and make the
color of newly inserted nodes as RED.
*If x is root, change color of x as BLACK

14.  Change color of parent and uncle as BLACK.
 Color of grand parent as RED.
 Change x = x’s grandparent, repeat steps for new x.

15. *Left Left Case (p is left child of g and x is left child of p)
*Left Right Case (p is left child of g and x is right child
of p)
Right Right Case (Mirror of case *)
Right Left Case (Mirror of case *)

20.  Red black tree are useful when we need
insertion and deletion relatively
frequent.
 Red-black trees are self-balancing so
these operations are guaranteed to be
O(logn).

21.  Balanced search trees have a height
that is always O(log N). One
consequence of this is that lookup,
insert, and delete on a balanced
search tree can be done in O(log N)
worst-case time.
 Red and black search trees have a
worst-case height of O(N)
 insert, and delete are O(N) in the
worst-case.
 Red-black trees are just one
example of a balanced search tree.

23.  Frequent insertions and deletions, then RBT should be preferred.
 Functional Programming
 Less structure changes to balance themselves
 Keep track of virtual memory for a process the start address of the
range server as the key
 A red–black tree use to organize pieces of comparable
data, such as numbers.
 It is used to implement CPU Scheduling.
 Most of the self-balancing BST library functions like
map and set in C++ (OR Tree Set and Tree Map in
Java) use Red Black Tree

24.  Execution of code
*Insertion
*Inorder
*Level order
*Deletion
*Inorder
*Level order

39.  https://www.geeksforgeeks.org/red-black-tree-set-2-
insert/
 https://www.geeksforgeeks.org/red-black-tree-set-3-
delete-2/
 https://www.quora.com/What-is-the-efficiency-of-
Red-Black-Trees-What-are-the-advantages-and-
disadvantages-of-RB-Trees
ANIMATION
 http://www.cs.armstrong.edu/liang/animation/web/R
BTree.html