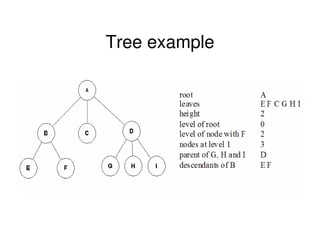
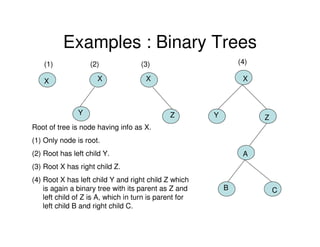
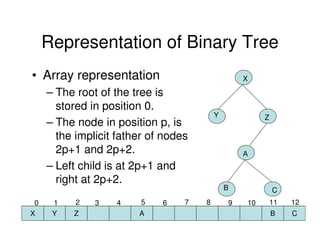
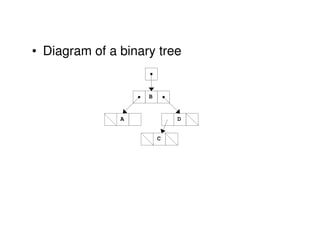
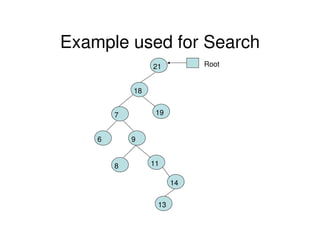
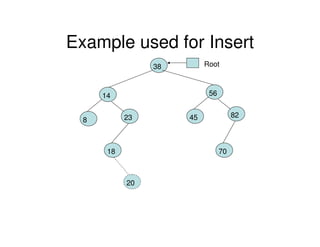
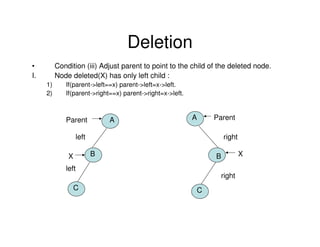
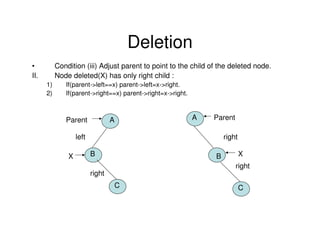
Binary trees are a non-linear data structure where each node has zero, one, or two child nodes. They are commonly used to represent hierarchical relationships. A binary tree has a root node at the top with child nodes below it. Binary trees can be empty or consist of a root node and left and right subtrees, which are also binary trees. They allow for efficient search, insert, and delete operations and can be represented using arrays or linked lists.

1. Non-Linear Data Structure
Binary Trees

2. Non-Linear Data Structure
• These data structures donot have their
elements in a sequence.
• Trees is an example.
• Trees are mainly used to represent data
containing a hierarchical relationship
between elements, ex : records, family
trees and table of contents.

3. Tree example

4. Trees
• Tree nodes contain two or more links
– All other data structures we have discussed
only contain one
• Binary trees
– All nodes contain two links
• None, one, or both of which may be NULL
– The root node is the first node in a tree.
– Each link in the root node refers to a child
– A node with no children is called a leaf node

5. Binary Trees
• Special type of tree in which every node or
vertex has either no children, one child or
two children.
• Characteristics :
• Every binary tree has a root pointer which
points to the start of the tree.
• A binary tree can be empty.
• It consists of a node called root, a left subtree
and right subtree both of which are binary
trees themselves.

6. Examples : Binary Trees
X X X X
Y YZ Z
A
B C
(1) (2) (3) (4)
Root of tree is node having info as X.
(1) Only node is root.
(2) Root has left child Y.
(3) Root X has right child Z.
(4) Root X has left child Y and right child Z which
is again a binary tree with its parent as Z and
left child of Z is A, which in turn is parent for
left child B and right child C.

7. Properties of Binary Tree
• A tree with n nodes has exactly (n-1) edges or
branches.
• In a tree every node except the root has exactly
one parent (and the root node does not have a
parent).
• There is exactly one path connecting any two
nodes in a tree.
• The maximum number of nodes in a binary tree
of height K is 2K+1 -1 where K>=0.

8. Representation of Binary Tree
• Array representation
– The root of the tree is
stored in position 0.
– The node in position p, is
the implicit father of nodes
2p+1 and 2p+2.
– Left child is at 2p+1 and
right at 2p+2.
X
Y Z
A
B C
Y AZ
0 2 3 4 5 6 71 8
B C
10 11 12
X
9

9. Representation of Binary Tree
• Linked List
• Every node will consists of information, and two
pointers left and right pointing to the left and right
child nodes.
struct node
{
int data;
struct node *left;
struct node *right;
};
• The topmost node or first node is pointed by a root
pointer which will inform the start of the tree. Rest of
the nodes are attached either to left if less than parent
or right if more or equal to parent.

10. • Diagram of a binary tree
B
A D
C

11. Operations on Binary Tree
• Searching an existing node.
• Inserting a new node.
• Deleting an existing node.
• Traversing the tree.
• Preorder
• Inorder
• Postorder

12. Search Process
• Initialize a search pointer as the root pointer.
• All the data is compared with the data stored in each
node of the tree starting from root node.
• If the data to be searched is equal to the data of the
node then print “successful” search.
• Else if the data is less than node’s data move the pointer
to left subtree. Else data is more than node’s data move
the pointer to right subtree.
• Keep moving in the tree until the data is found or search
pointer comes to NULL in which case it is an
“unsuccessful” search.

13. Example used for Search
21
18
197
6 9
8 11
14
13
Root

14. Example : Search
• Initialize temp as root pointer which is node having 21.
• Loop until temp!=NULL or ITEM found
• Compare item=9 with the root 21 of the tree, since
9<21, proceed temp to the left child of the tree.
• Compare ITEM=9 with 18 since 9<18 proceed temp
to the left subtree of 18, which is 7.
• Compare ITEM=9 with 7 since 9>7 proceed temp to
right subtree of the node which holds a value 7.
• Now ITEM=9 is compared with the node which holds
value 9 and since 9 is found the searching process
ens here.

15. Insert Process
• For node insertion in a binary search tree, initially the
data that is to be inserted is compared with the data of
the root data.
• If the data is found to be greater than or equal to the
data of the root node then the new node is inserted in
the right subtree of the root node, else left subtree.
• Now the parent of the right or left subtree is considered
and its data is compared with the data of the new node
and the same procedure is repeated again until a NULL
is found which will indicate a space when the new node
has to be attached. Thus finally the new node is made
the appropriate child of this current node.

16. Example used for Insert
38
14
238
Root
56
8245
18 70
20

17. Example : Insert
• Suppose the ITEM=20 is the data part of the new node
to be inserted in the tree and the root is pointing to the
start of the tree.
• Compare ITEM=20 with the root 38 of the tree. Since 20
< 38 proceed to the left child of 38, which is 14.
• Compare ITEM=20 with 14, since 20 > 14 proceed to the
right child of 14, which is 23.
• Compare ITEM=20 with 23 since 20 < 23 proceed to the
left child of 23 which is 18.
• Compare ITEM=20 with 18 since 20 > 18 and 18 does
not have right child, 10 is inserted as the right child of 18.

18. Deletion
• Condition (i) Print message data not found.
• Condition (ii) Since no children so free the node
& make either parent->left=NULL or parent-
>right=NULL.
A A
B C
Parent Parent
left right
X X
In the example1,
parent->left==x so free(x) and
make parent->left=NULL.
In the example2,
parent->right==x so free(x) and
make parent->right=NULL.

19. Deletion
• Condition (iii) Adjust parent to point to the child of the deleted node.
I. Node deleted(X) has only left child :
1) If(parent->left==x) parent->left=x->left.
2) If(parent->right==x) parent->right=x->left.
A A
B
Parent Parent
left right
X XB
C C
left
right

20. Deletion
• Condition (iii) Adjust parent to point to the child of the deleted node.
II. Node deleted(X) has only right child :
1) If(parent->left==x) parent->left=x->right.
2) If(parent->right==x) parent->right=x->right.
A A
B
Parent Parent
left right
X XB
C C
right
right

21. Deletion
• Condition (iv) solution more complex as X has two children,
• Find inorder successor of the node X. Inorder successor of any node will be first go to right of the
node and then from that node keep going left until NULL encountered, that will be the inorder
successor.
• Copy data of inorder successor to node X’s data.
• Place pointer at the inorder successor node. Now the inorder succesor will have zero or one child
only (so the complex problem is reduced to condition (iii)).
• Delete the inorder successor node by using logic of condition (ii) if no children or condition (iiii) if one
right child.
A
B
Parent
left
X
D
rightleft
C
E
left
A
E
Parent
left
X
D
rightleft
C
E
left
Here inorder successor E has
no children condition (ii)