The document discusses heap trees, which are tree-based data structures where all nodes follow a specific ordering. There are two main types: max-heaps, where the root node has the greatest value of its children, and min-heaps, where the root node has the minimum value. Heaps are often stored as arrays for efficient implementation of operations like insertion, deletion, and merging in logarithmic time. Common applications of heaps include priority queues, sorting algorithms, and finding order statistics.

1. HEAP TREE
BY
S.RAJAPRIYA
Assistant Professor
E-MAILID : rajapriya@vvvcollege.org

2. ۳ A heap is a tree-based data structure in which all the
nodes of the tree are in a specific order.
۳ For example, if X is the parent node of Y, then the value
of X follows a specific order with respect to the value
of Y and the same order will be followed across the tree.
۳ Generally, Heaps can be of two types:
Max-Heap: In a Max-Heap the key present at the
root node must be greatest among the keys present at all of
it’s children. The same property must be recursively true for
all sub-trees in that Binary Tree.
Min-Heap: In a Min-Heap the key present at the
root node must be minimum among the keys present at all of
it’s children. The same property must be recursively true for
all sub-trees in that Binary Tree.
HEAP TREE

3. HEAP DATA STRUCTURE
Min heap Max heap

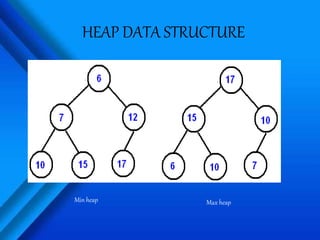
4. REPRESENTATION OF A HEAP TREE
Heaps are built
on arrays
Heaps are often stored
as arrays, one node
after the other, like
this:
An array can be used
to simulate a tree in
the following way :
If we are storing one
element at
index I then
Parent :will be stored
at index I/2
Left child : will be
stored at [2∗I]
Right child : will be
stored at [2∗I+1].
 Index of root will
be 1 in an array.

5. OPERATIONS OF A HEAP TREE
The Major operations required to be
performed on a heap tree are :
⁕ Insertion
⁕Deletion
⁕Merging

6. INSERTION OPERATION
1. Add the item to the bottom of the tree.To insert an item 7 to the heap tree
2. Compare the item with its parent. If the
new item is smaller, swap the two
3. Continue comparing and swapping, allowing
the new item to "bubble up" until the it's
larger than its parent.

7. DELETION OPERATION
The standard deletion operation on Heap is to delete the element
present at the root node of the Heap.
That is if it is a Max Heap, the standard deletion operation will delete
the maximum element and if it is a Min heap, it will delete the
minimum element.
Process of Deletion:
 Replace the root node by the last node in the Heap tree.
 Delete the last element from the Heap.
 Compare the item with its children.
 If it's larger than either child, swap the item with the smaller of
the two children.
 Continue comparing and swapping, allowing the item to "bubble
down" until it's smaller than its children.

8. ILLUSTRATION

9. APPLICATIONS OF HEAP TREE
Some of the Heap tree applications are:
⁕ Sorting using heap tree
We can use heaps in sorting the elements in a specific order in
efficient time.
⁕ Heap as a Priority queue
Priority queues can be efficiently implemented using Binary Heap
because it supports insert(), delete() and extractmax(), decreaseKey()
operations in O(logn) time
⁕Order statistics
The Heap data structure can be used to efficiently find the kth
smallest (or largest) element in an array.
.

10. Advantages :
Quickly access the smallest item. Binary heaps
allow you to grab the smallest item (the root)
in O(1)O(1) time, while keeping other operations relatively
cheap (O(lg(n))O(lg(n)) time).
Space efficient. Binary heaps are usually
implemented with arrays, saving the overhead cost of storing
pointers to child nodes.
Disadvantages :
Limited interface. Binary heaps only provide easy
access to the smallest item. Finding other items in the heap
takes O(n)O(n) time, since we have to iterate through all the
nodes.
ADVANTAGES & DISADVANTAGES