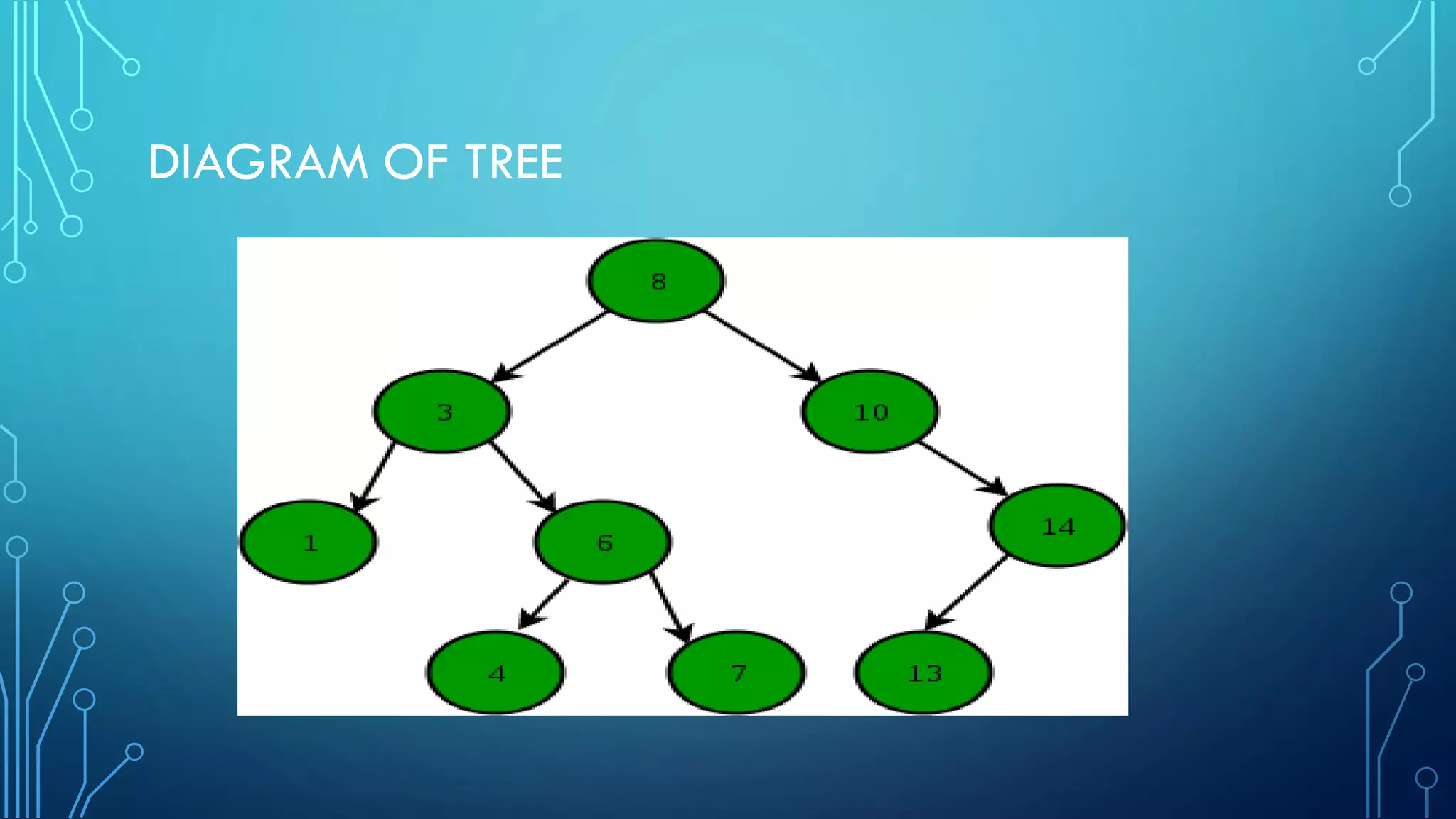
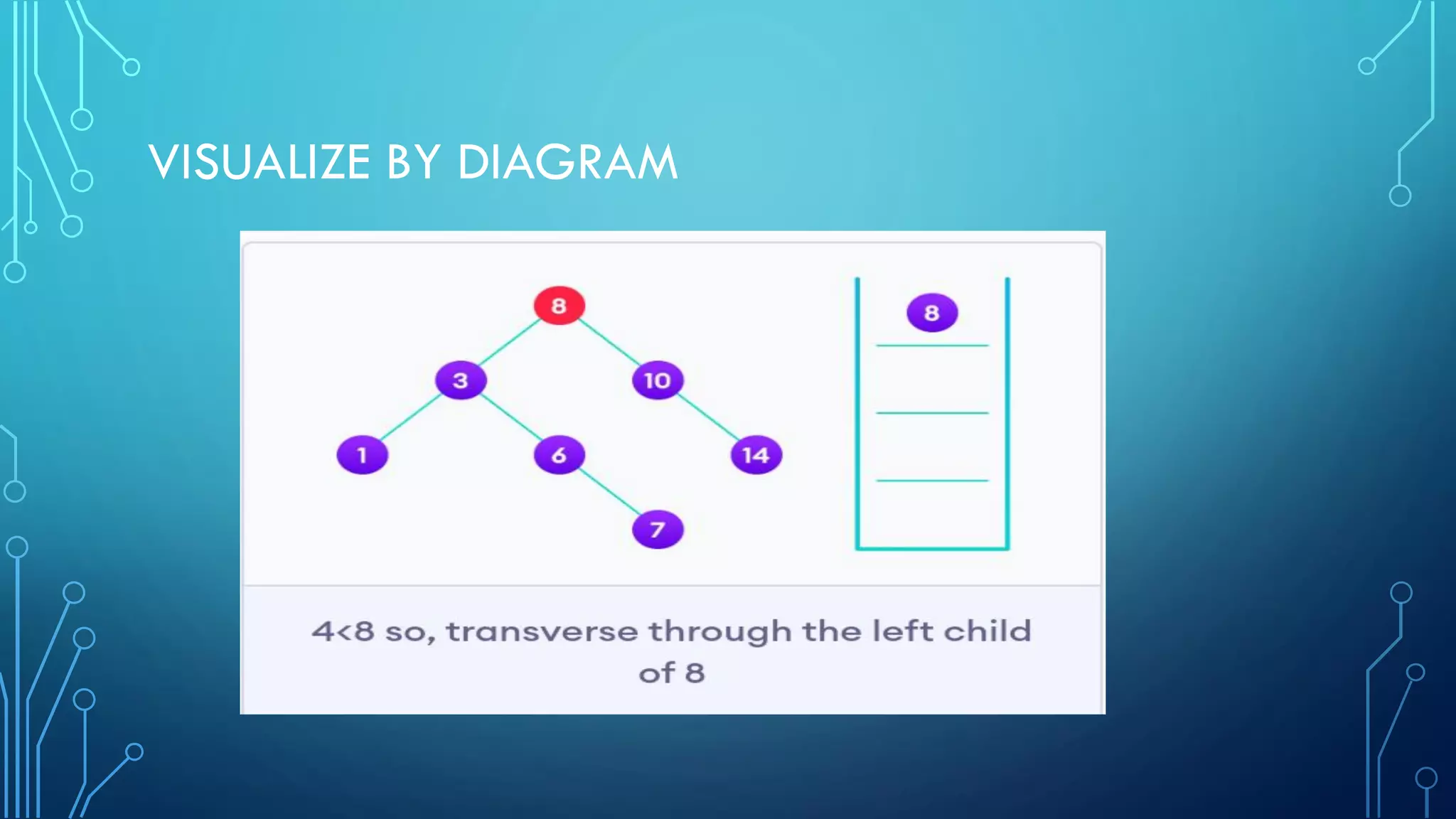
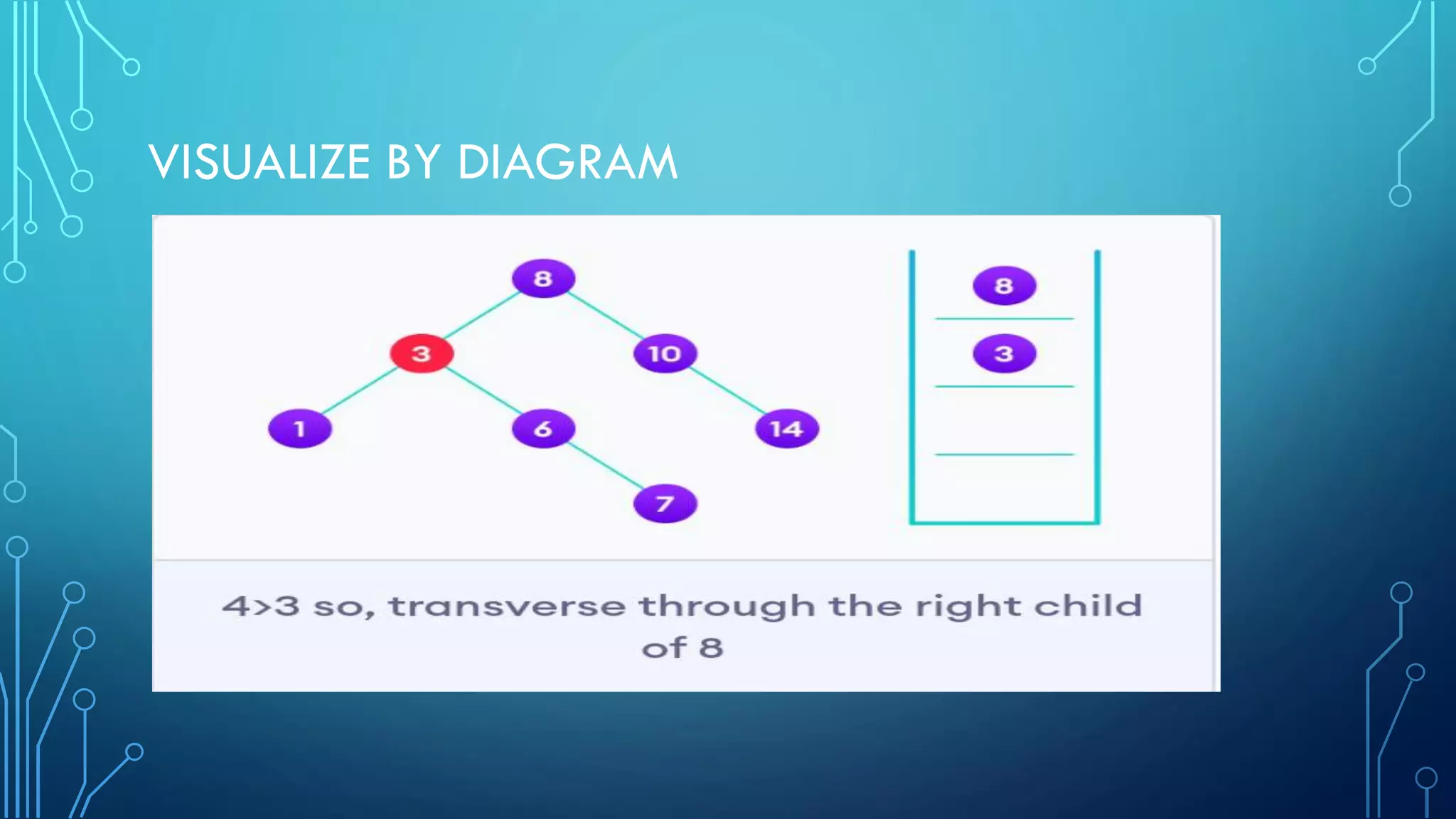
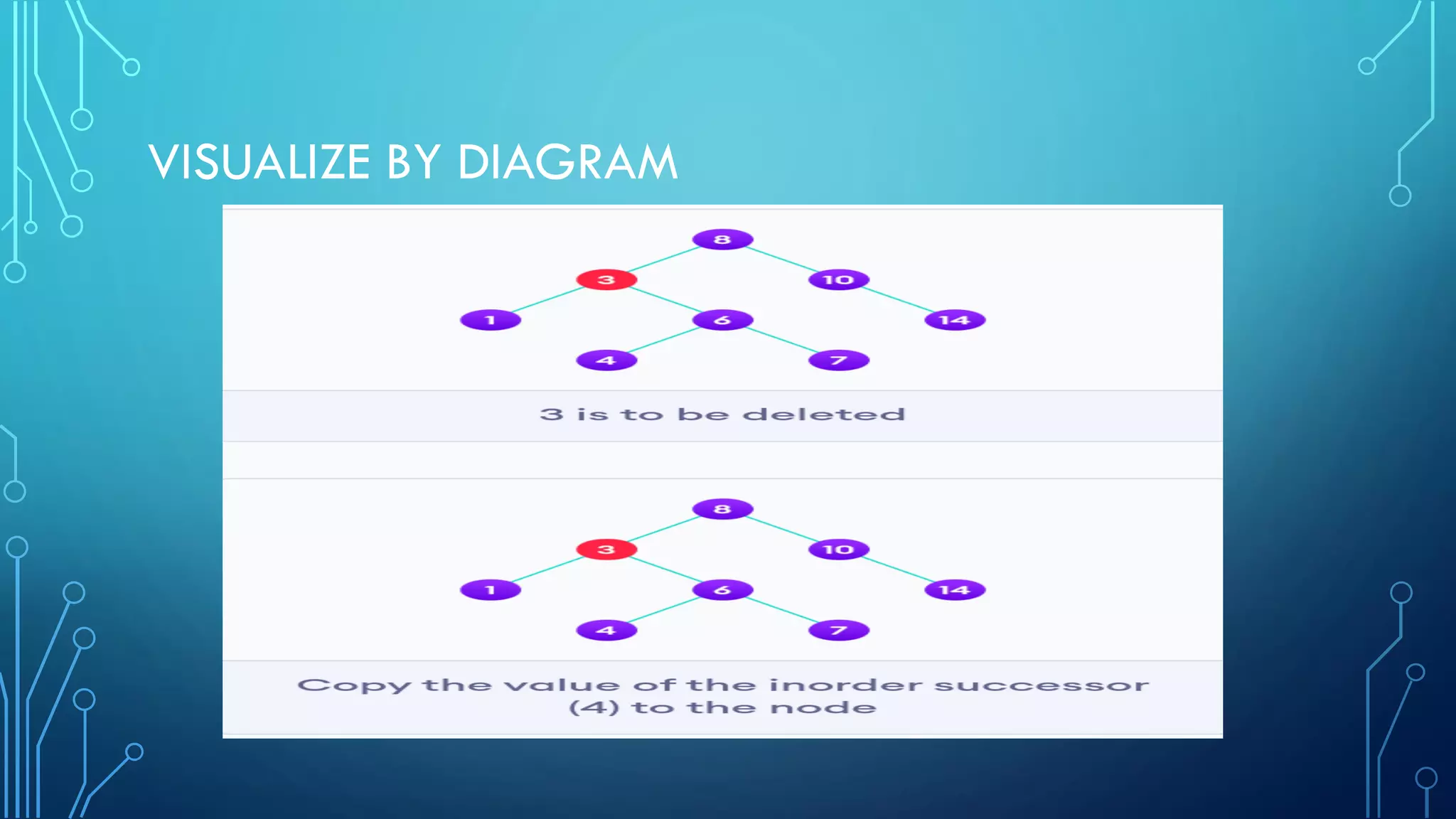
This document discusses binary search trees (BST), including: - The definition and properties of a BST, with nodes organized based on key values. - Common BST operations like insertion, deletion, and searching in logarithmic time. - Advantages of BSTs like efficient searching and working compared to arrays/lists. - Applications of BSTs in databases, dictionaries, and evaluating expressions. - Visual examples of searching, inserting, and deleting nodes from a BST.

1. PRESENTATION
BINARY SEARCH TREE OPERATION

2. DEFINATION OF BINARY SEARCH TREE
Binary Search Tree is a node-based binary tree data
structure which has the following properties.
•The left subtree of a node contains only nodes with key
lesser than the node's key.
•The right subtree of a node contains only
node with keys greater than the node's key.

3. DIAGRAM OF TREE

4. BASIC OPERATION
•#1) INSERT
•#2)DELETE
•#3)SEARCH
•#4)TRAVERSAL

5. ADVANTAGES OF BST
•#1)Searching Is Very Efficient
We have all the nodes of BST in a specific order, hence searching for a
particular item is very efficient and faster. This is because we need not search
the entire and compare all nodes.
We just have to compare the root node to the item which we are searching and
then we decide whether we need to search in the left or right subtree.

6. ADVANTAGES OF BST
•#2) Efficient Working When Compared To
Array And Linked Lists
When we search an item in case of BST, we get rid of half of the left or right
subtree at every step thereby improving the performance of search operation.
This is in contrast to array or linked list in which we need to compare all the
items sequentially to search a particular.

7. ADVANTAGES OF BST
•#3)Insert And Delete Are Faster
Insert and delete operations also are faster when compared to other data
structures like Linked Lists and Array.

8. APPLICTION OF BST
• BST is used to implement multilevel indexing in database application.
• BST is also used to implement constructs like a dictionary.
• BST can be used to implement various efficient searching algorithms.
• BST is also used in applications that require a sorted list as input
like the online stories.
• BSTs are also used to evaluate expression using expression trees.

9. CONCLUTION
Binary search trees(BST) are a variation of the binary tree and are widely used
in the software field. They are also called ordered binary trees as each node in
BST is placed according to a specific order.
Inorder traversal of BST gives us the sorted sequence of items in ascending
order. When BSTs are used for searching, it is very efficient and is done within
no time. BSTs are also used for a variety of application like Huffman's coding,
Multilevel index in database ,etc.

10. OPERATIONS

11. SEARCH OPERATION
The Algorithm depends on the property of BST that if each left subtree has
value below root and each right subtree has value above the root.
If the value is below the root, we can say for sure that the value is not in the
right subtree; we need to only search in the left subtree and if the value above
root, we can say for sure that value is not in the left subtree; we need to only
search in the right subtree.

12. VISUALIZE BY DIAGRAM

13. VISUALIZE BY DIAGRAM

14. VISUALIZE BY DIAGRAM

15. VISUALIZE BY DIAGRAM

16. INSERT OPERATION
Inserting a value in the correct position is similar to searching because we try to
maintain the rule that the left subtree is lesser than root and the right subtree is
larger than root.
We keep going to either right subtree depending on the value and when we
reach a point left or right subtree is null, we put the new code there.

17. VISUALIZE BY DIAGRAM

18. VISUALIZE BY DIAGRAM

19. VISUALIZE BY DIAGRAM

20. VISUALIZE BY DIAGRAM

21. DELETE OPERATION
There are three cases for deleting a node from a binary
search tree.

22. CASE-1
In the first case, the node to be delete is the leaf node. In such a case, simply
delete the node from the tree.

23. CASE-2
In the second case, the node to be deleted lies has a single child node.
In such cases follow the step below
1.Replace that node with its child node.
2.Remove the child node from its original position.

25. CASE-3
• In the third case, the node to be deleted has two children. In such a case
follow the steps below:
1.Get the inorder successor of that.
2.Replace the node with the inorder successor.
3.Remove the inorder successor from its original position.

26. VISUALIZE BY DIAGRAM

27. VISUALIZE BY DIAGRAM

28. PRESENTED BY:
•Ehsan ul khaliq (F20-BsCS-5004)
•Faisal Shehzad (F20-BsCS-5030)
•Kamran Zafar (F20-BsCS-5039)