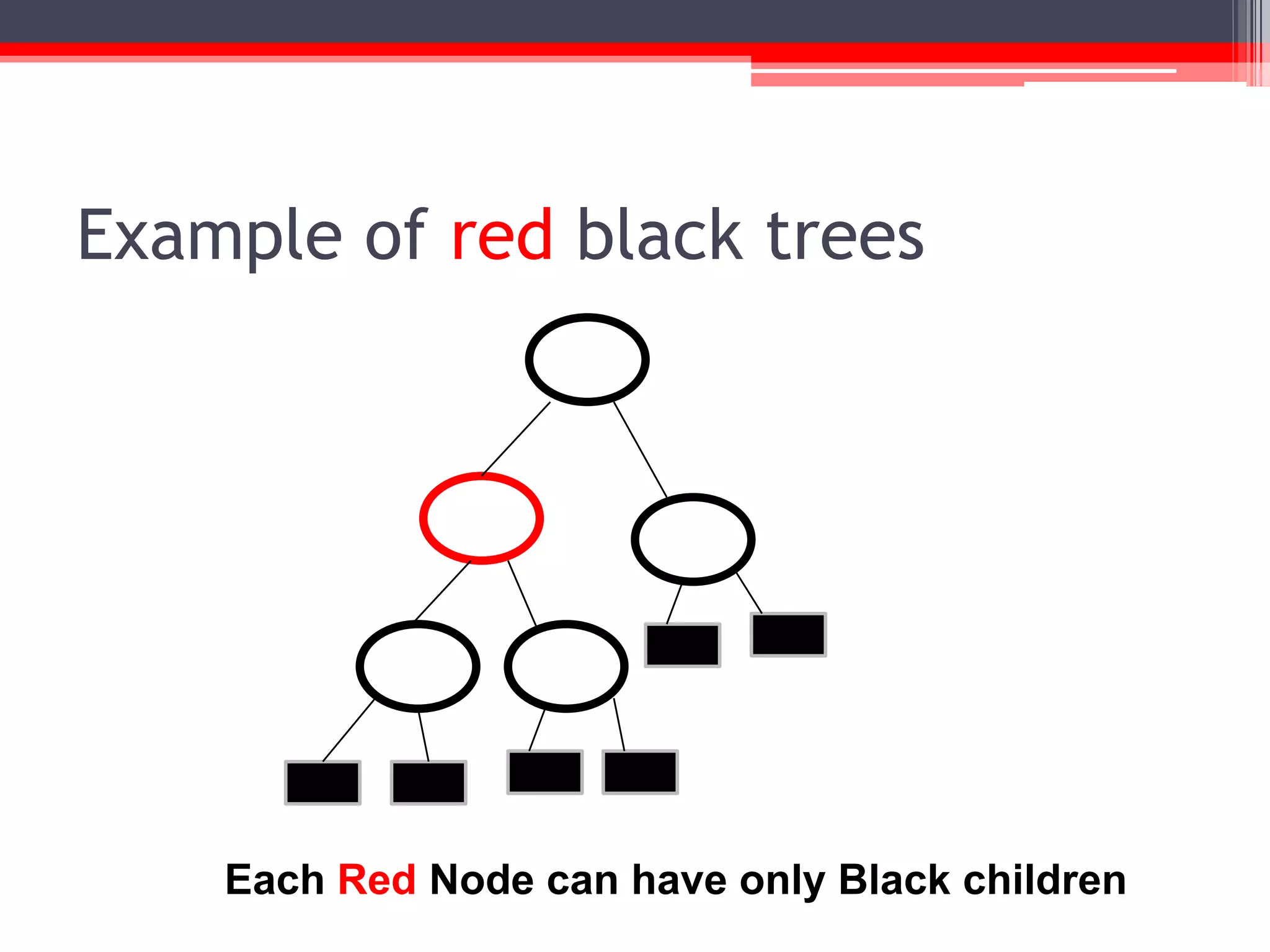
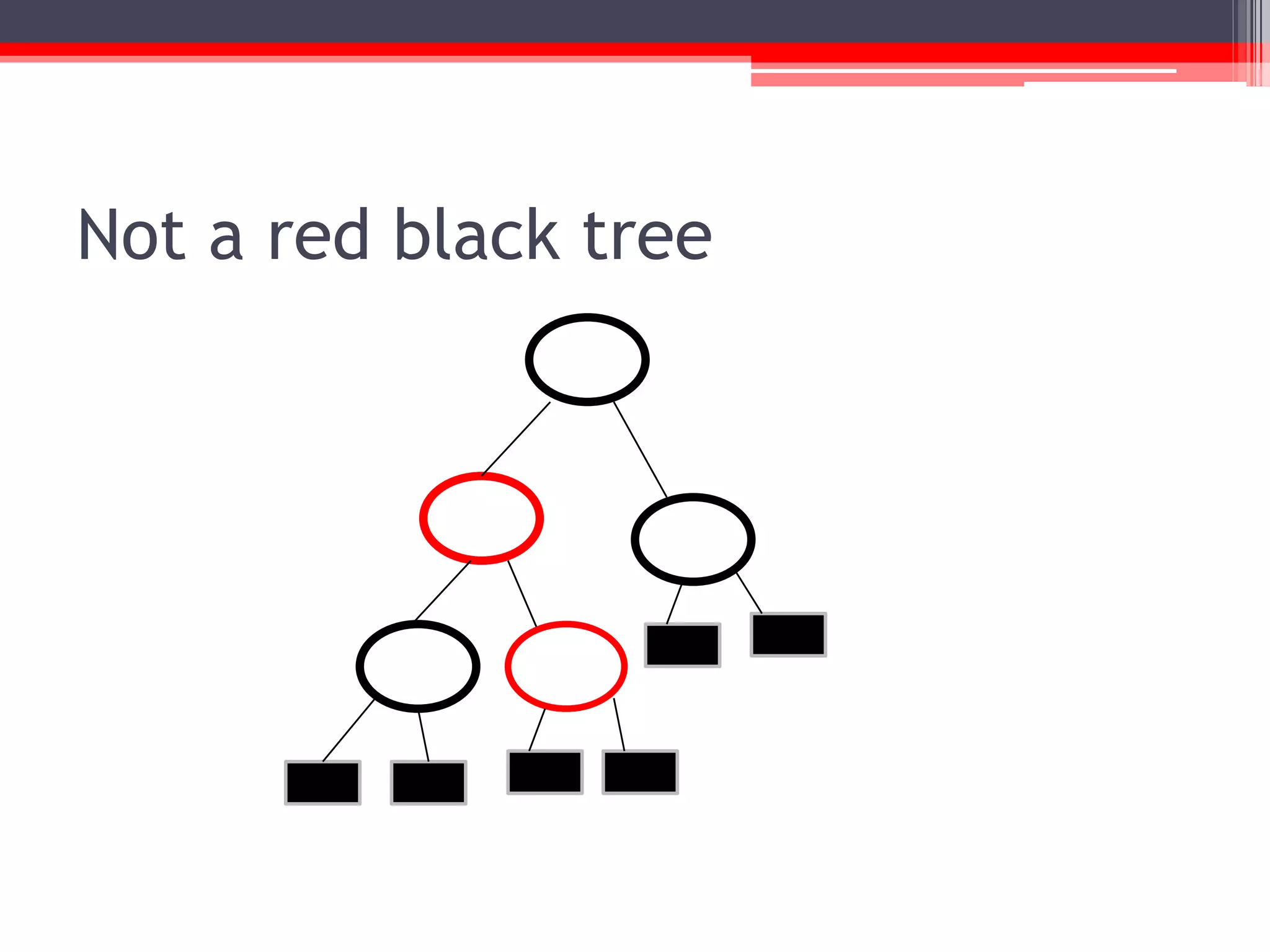
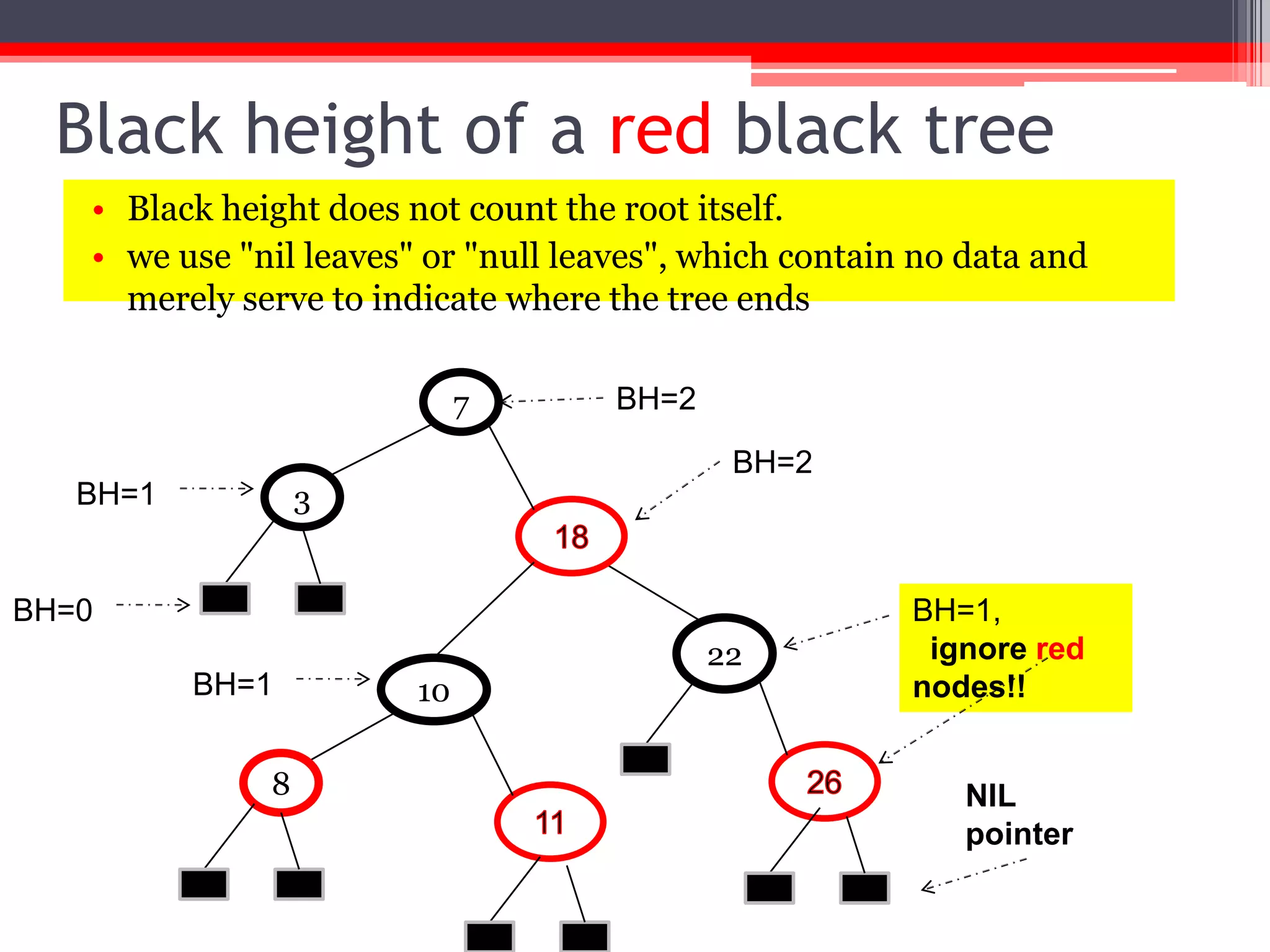
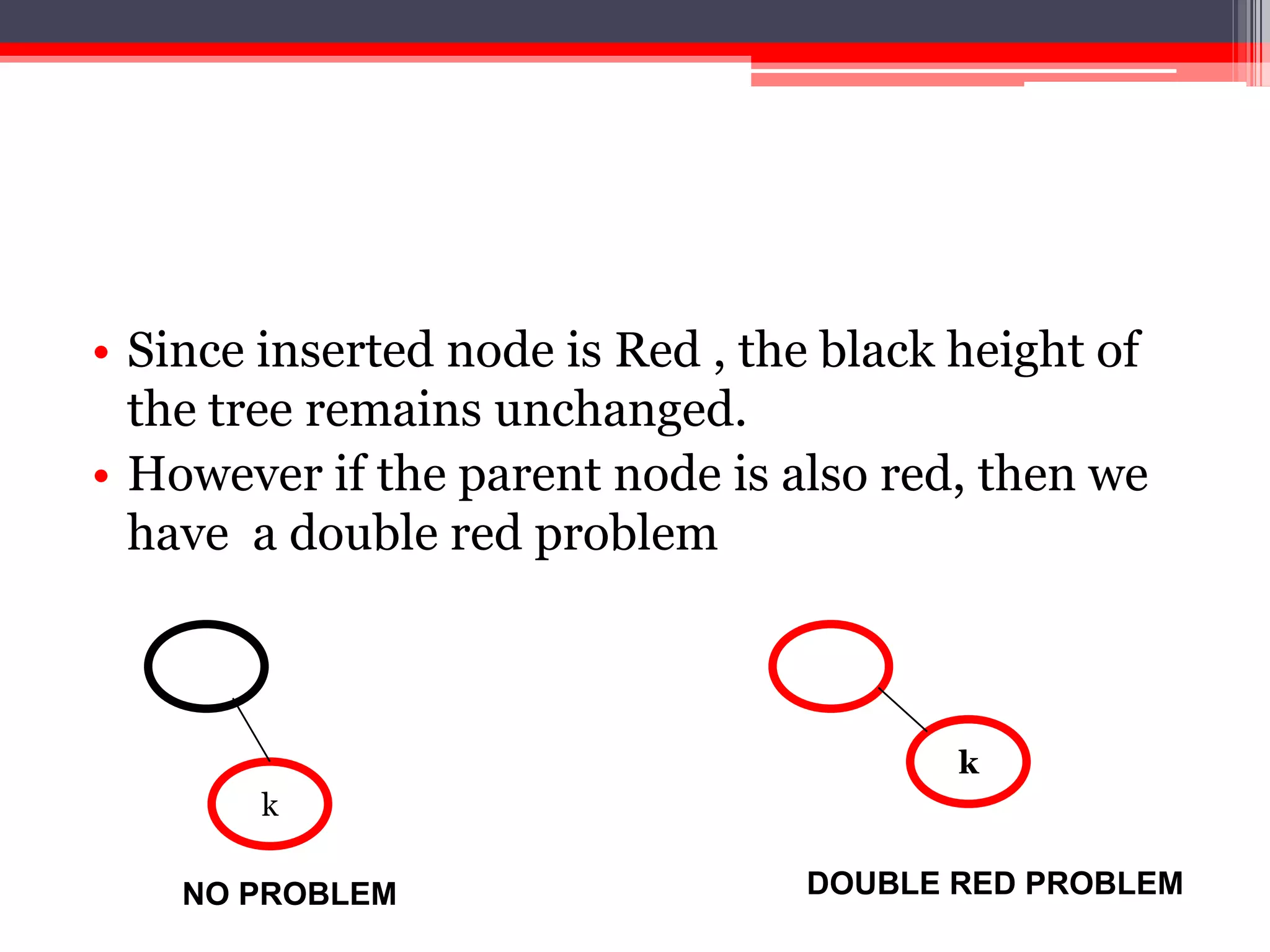
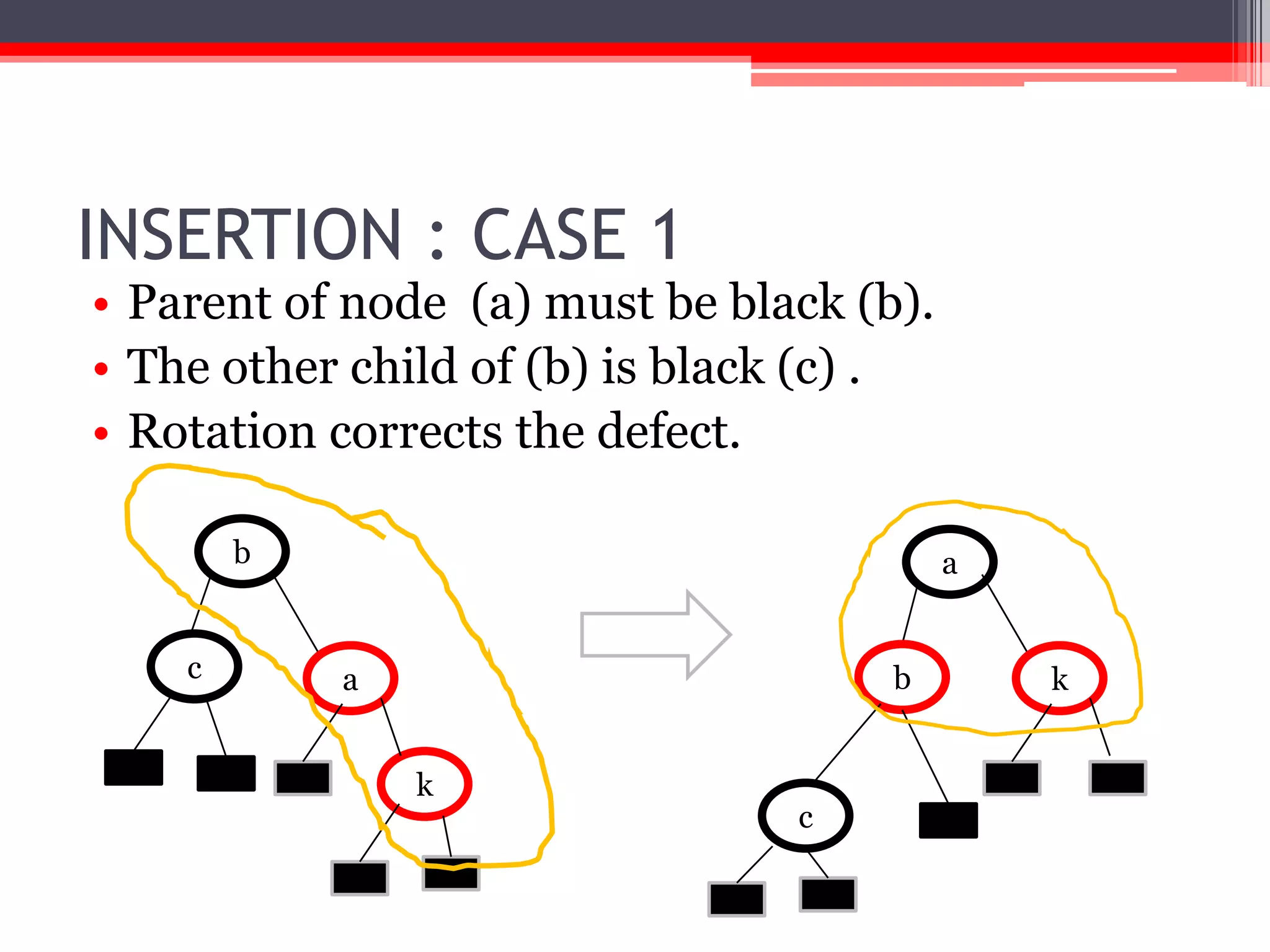
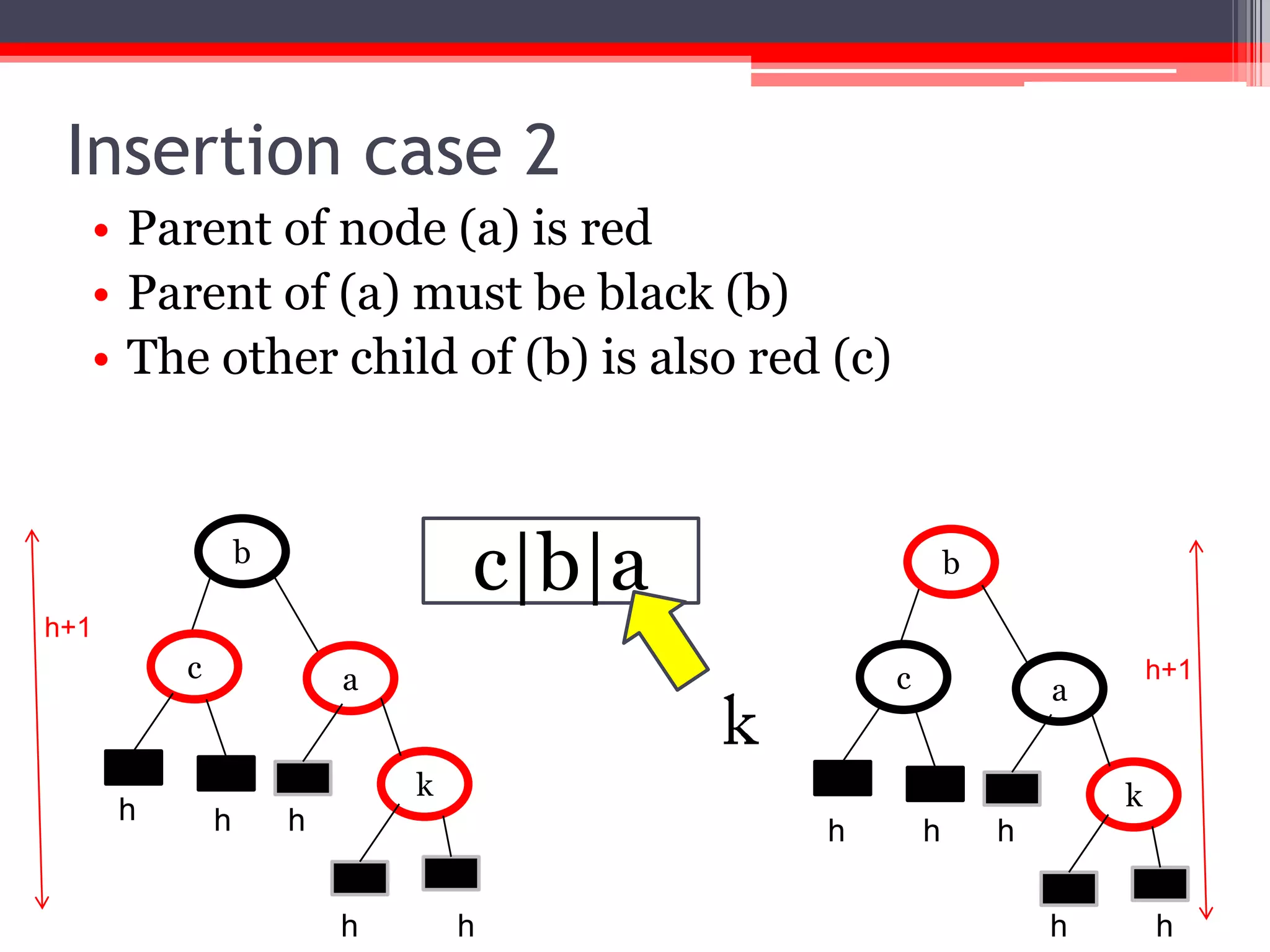
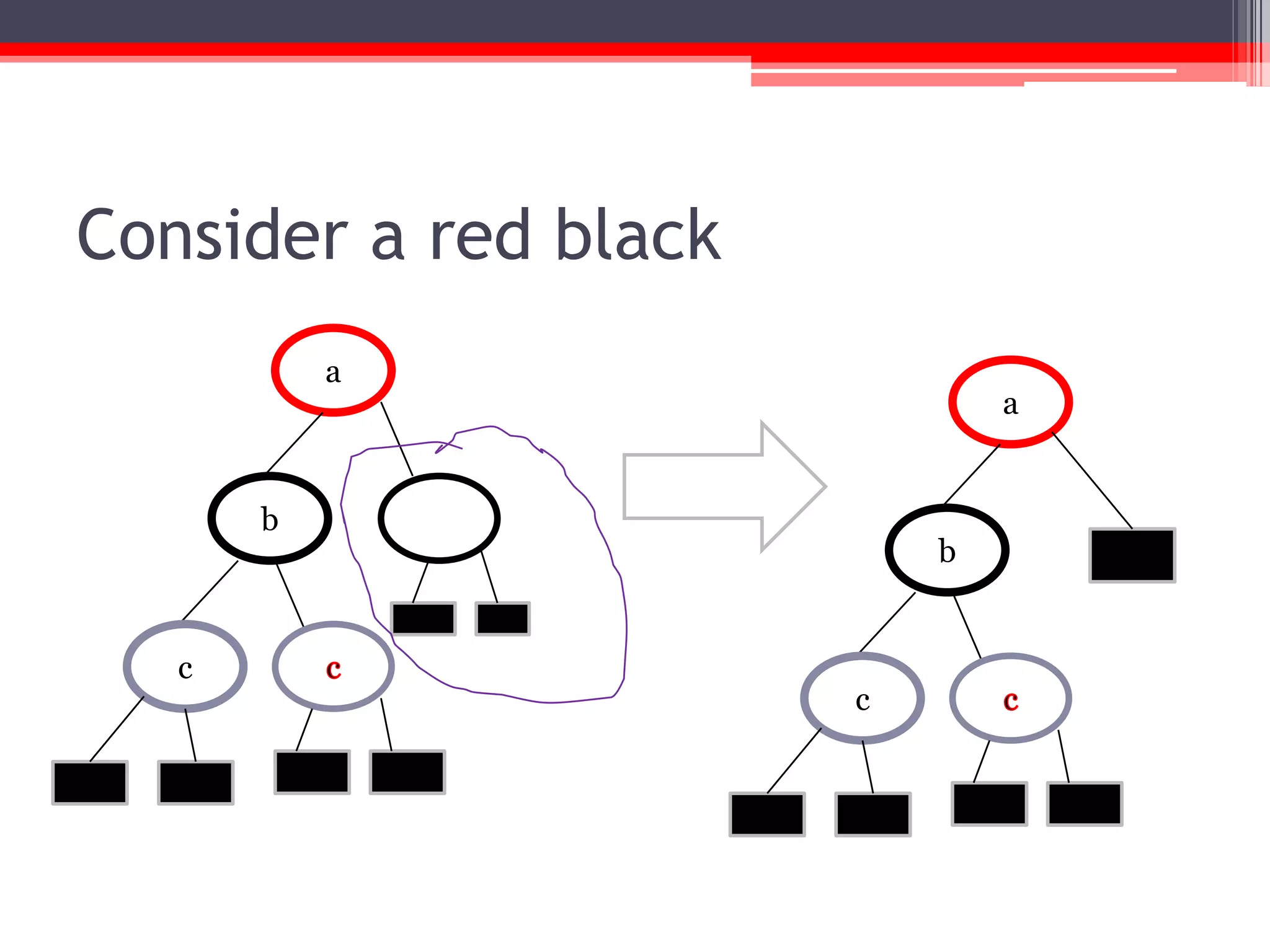
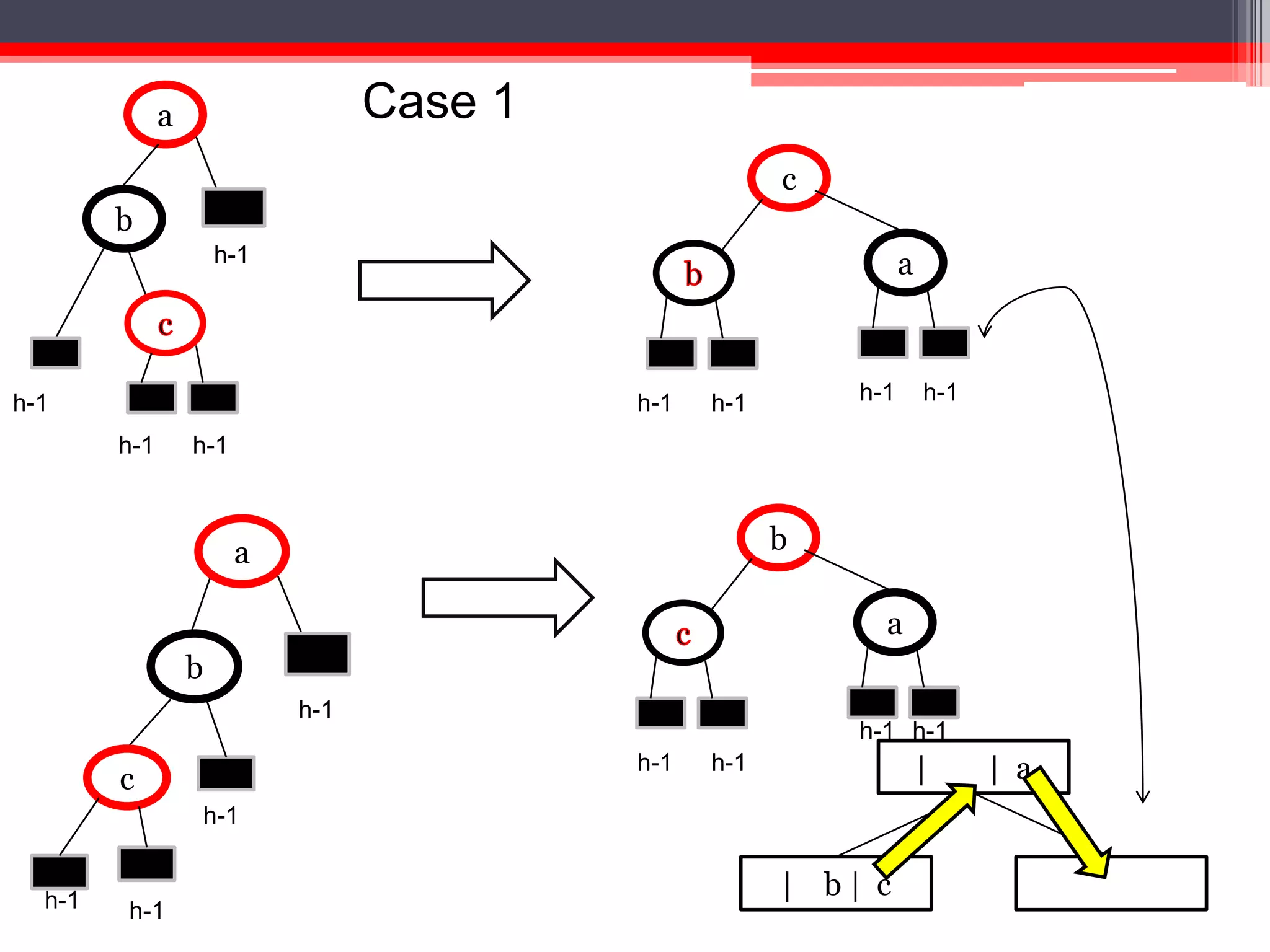
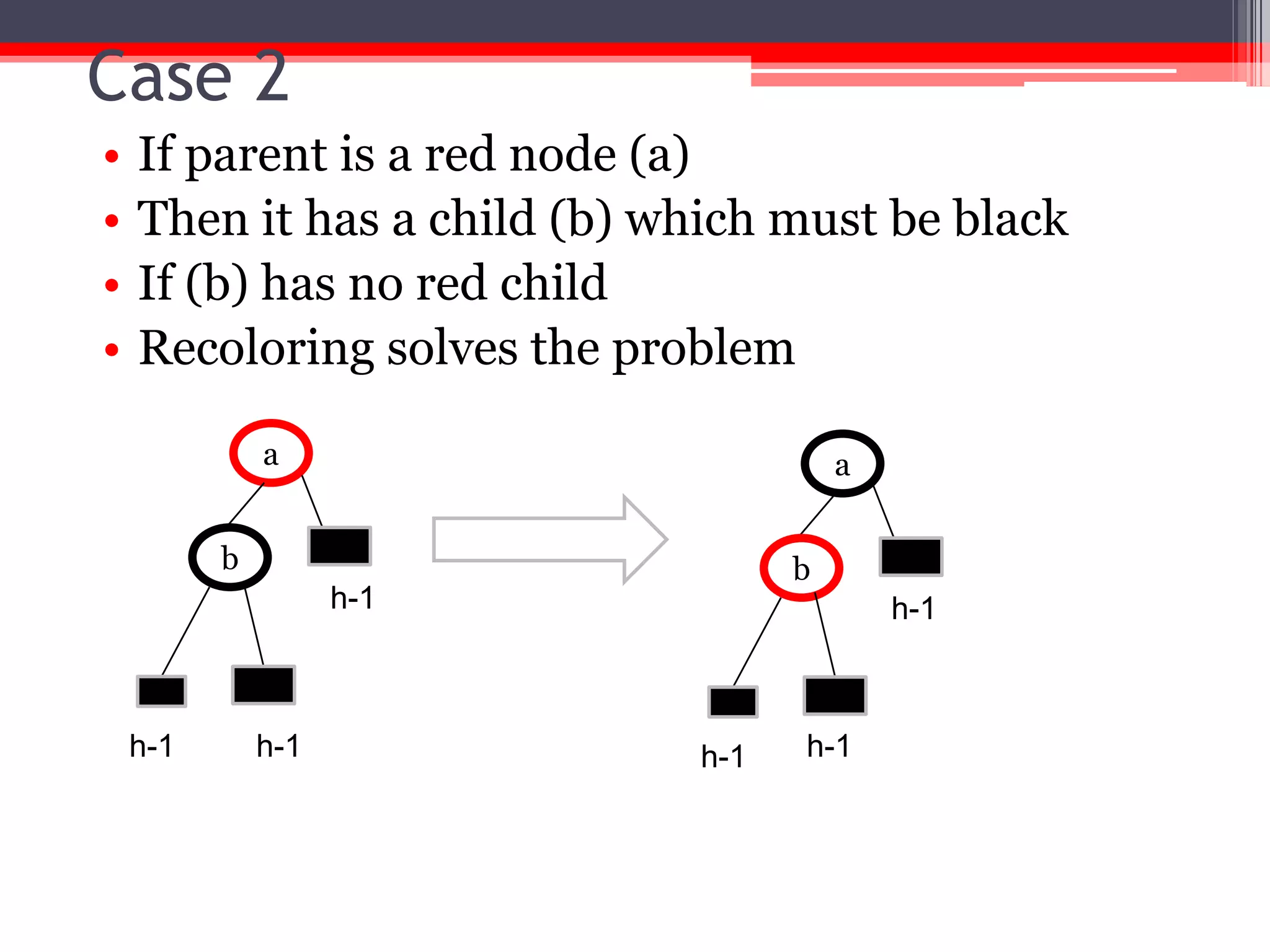
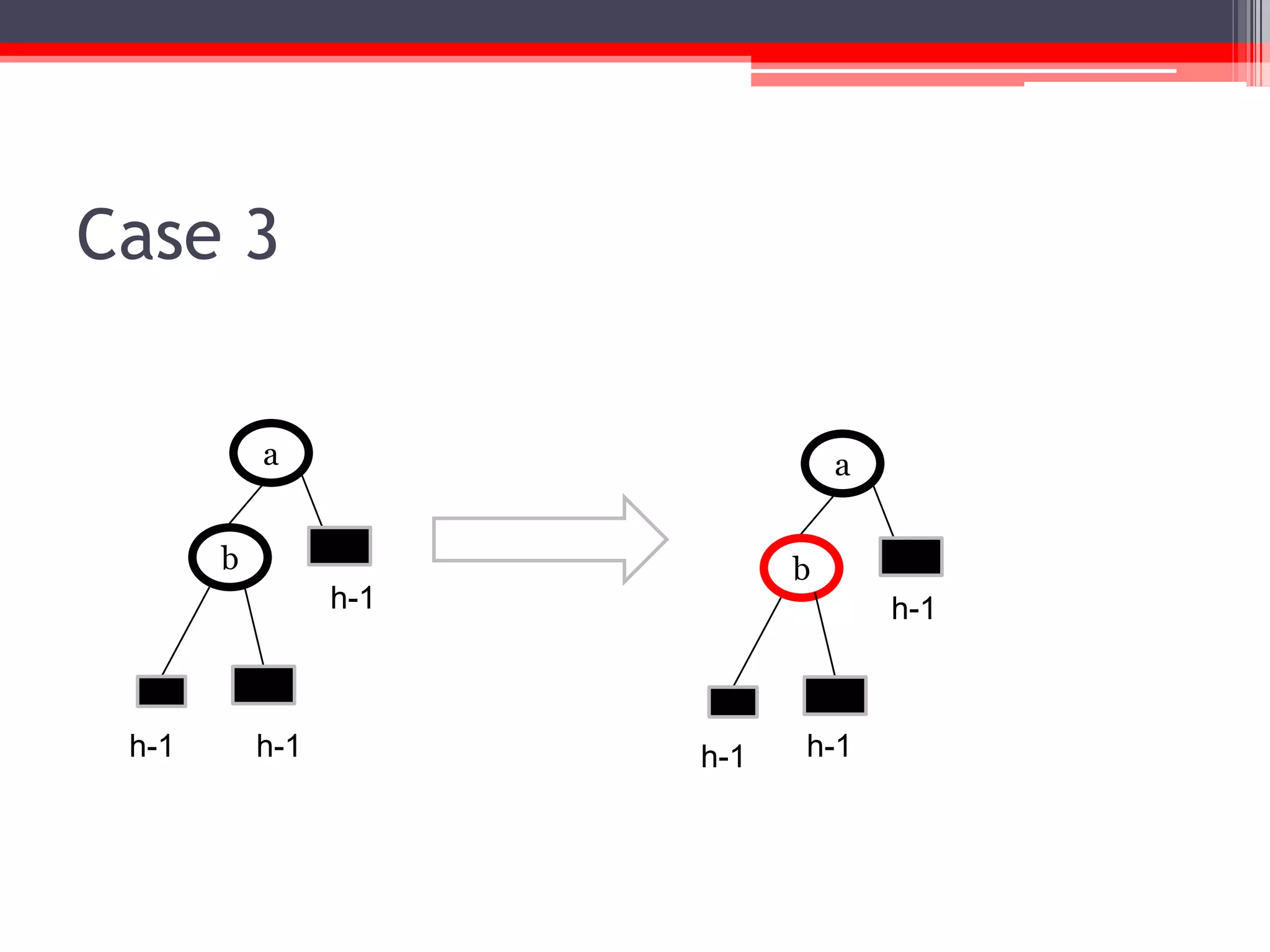
The document provides an overview of red-black trees, a type of self-balancing binary search tree characterized by color attributes of its nodes. Key operations like insertion and deletion are discussed, including how to handle scenarios such as double red problems and the importance of maintaining balance. References to additional resources and educational materials on algorithms and data structures are also included.

1. PRAVIN D’SILVA
1109
MCA , GOA UNIVERSITY

2. Acknowledgement
I would like express my sincere gratitude to Dr.
Jyoti Pawar, for the support and guidance as
well as the feedback she has provided
throughout this study.

3. Definition
• A red-black tree is a type of self balancing
binary search tree, with one extra attribute for
each node: the colour, which is either red or
black.
• A red–black tree is a binary search tree that
inserts and deletes in such a way that the tree is
always reasonably balanced.

4. Balanced binary tree
• A non-empty binary tree T is
balanced if:
1) Left subtree of T is balanced
2) Right subtree of T is balanced
3) The difference between heights of
left subtree and right subtree is not
more than 1.

5. Red-Black tree
• Recall binary search tree
▫ Key values in the left subtree <= the node value
▫ Key values in the right subtree >= the node value
• Operations:
▫ insertion, deletion
▫ Search, maximum, minimum, successor, predecessor.
▫ O(h), h is the height of the tree.

6. Red-black trees
•
Definition: a binary tree, satisfying:
1.
2.
3.
4.
5.
•
•
Every node is red or black
The root is black
Every leaf is NIL and is black
If a node is red, then both its children are black
For each node, all paths from the node to
descendant leaves contain the same number of
black nodes.
Purpose: keep the tree balanced.
Other balanced search tree:
▫
AVL tree, 2-3-4 tree, Splay tree, Treap

7. Example of red black trees
Each Red Node can have only Black children

8. Not a red black tree

9. Black height of a red black tree
• Black height does not count the root itself.
• we use "nil leaves" or "null leaves", which contain no data and
merely serve to indicate where the tree ends
7
BH=2
BH=2
3
BH=1
BH=0
22
BH=1
8
10
BH=1,
ignore red
nodes!!
NIL
pointer

10. Complexity
• The persistent version of red-black trees
requires O(log n) space for each insertion or
deletion.

11. Some operations in log(n)
• Search, minimum, maximum,
successor, predecessor.
• Let us discuss insert and delete.

12. Inserting in a red black tree
• Let k be the key being inserted.
• As in case of a BST, we first search for k; this
gives us the place where we have to insert k.
• We create a new node with key k and insert it at
this place
• The new node is colored red.

13. • Since inserted node is Red , the black height of
the tree remains unchanged.
• However if the parent node is also red, then we
have a double red problem
k
k
NO PROBLEM
DOUBLE RED PROBLEM

14. INSERTION : CASE 1
• Parent of node (a) must be black (b).
• The other child of (b) is black (c) .
• Rotation corrects the defect.
b
c
a
b
a
k
c
k

15. Insertion case 2
• Parent of node (a) is red
• Parent of (a) must be black (b)
• The other child of (b) is also red (c)
c|b|a
b
b
h+1
c
h
c
a
k
h
k
h
h
h
h+1
a
h
h
h
h
h

16. Deletion
• To delete a node we proceed as in a BST
• Hence the node which is deleted is the parent of
an external node
• Hence it is either a leaf or parent of a leaf
• Steps:
▫
▫
▫
▫
Search
Identify
Leaf, then delete
If internal node, find successor or predecessor,
swap, then delete the successor or predecessor

17. Consider a red black
a
a
b
c
b
c

18. Case 1
a
c
b
a
h-1
h-1
h-1
h-1
h-1
h-1
h-1
h-1
b
a
a
b
h-1
h-1 h-1
h-1
c
|
h-1
h-1
h-1
h-1
| b| c
| a

19. Case 2
•
•
•
•
If parent is a red node (a)
Then it has a child (b) which must be black
If (b) has no red child
Recoloring solves the problem
a
a
b
b
h-1
h-1
h-1
h-1
h-1
h-1

20. Case 3
a
a
b
b
h-1
h-1
h-1
h-1
h-1
h-1

21. Deletion Summary
• In most cases, deletion can be completed by
simple rotation/ coloring.
• In case 3, the height of the subtree reduces and
so we need to proceed up the tree
• But in case 3, we only recolor the nodes
• Thus, if we proceed up the tree, then we only
need to recolor. Eventually we would do a
rotation.

22. References
• "Introduction to Algorithms, Third Edition," by Thomas H.
Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein.
• Lecture Series on Data Structures and Algorithms by Dr. Naveen
Garg, Department of Computer Science and Engineering, IIT Delhi.
http://nptel.iitm.ac.in
• Lecture 10: Red-black Trees, Rotations, Insertions, Deletions:
http://videolectures.net/mit6046jf05_demaine_lec10/
• http://mitpress.mit.edu/algorithms/solutions/chap13-solutions.pdf
• http://www.cs.purdue.edu/homes/ayg/CS251/slides/chap13c.pdf
• Left leaning Red black trees
• http://www.cs.princeton.edu/~rs/talks/LLRB/RedBlack.pdf
• http://www.cs.princeton.edu/~rs/talks/LLRB/LLRB.pdf

23. Thank
You