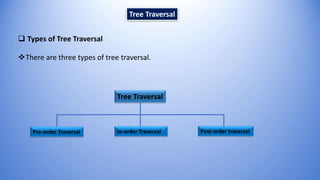
The document discusses tree traversal in the context of discrete mathematics, detailing its definition and types: pre-order, in-order, and post-order traversal. It provides the sequence of node visits for each traversal type and includes algorithms for implementation. Examples are given for each traversal method to illustrate the concepts.

1. Dept. of Computer science of Engineering
Batch: Spring 2022- 221-DA
Date: 10/05/2022
Course teacher: Md. Suntanul Islam Ovi
Subject: Discrete Math
Topic: Tree Traversal

2. Md. Sabbir Hossain
ID: 221902126
Md. Israil Fakir
ID: 221902125
Dina Azad
ID: 221902123
Md. Emam Hossain
ID: 221902124

3. Tree Traversal
 What is Tree Traversal ?
 Tree traversal means visiting each node of the tree
However, in tree data structures, there are multiple
ways to traverse it.

4. Tree Traversal
 Types of Tree Traversal
There are three types of tree traversal.
In-order Traversal
Tree Traversal
Pre-order Traversal Post-order traversal

5. Pre-order Traversal
Preorder traversal
1. Visit root node
2. Visit all the nodes in the left subtree
3. Visit all the nodes in the right subtree
 In this traversal method, the root node is visited first, then the
left subtree and finally the right subtree

6. Pre-order Traversal
Example:
Solution: 1 2 4 5 3

7. Pre-order Traversal
Algorithm: Pre-order traversal
procedure preorder (T: Ordered rooted tree )
r:=root of T
List r
For each child c of r from left to right
begin
T(c):= subtree with c as its root
Preorder ( T(c))
end
T
r
b c
d e
g
f
k
h i j

8. In-order Traversal
In this traversal method, the left subtree is visited
first, then the root and later the right sub-tree. We
should always remember that every node may
represent a subtree itself.
In-order traversal
1. Visit all the nodes in the left subtree
2. Visit root node
3. Visit all the nodes in the right subtree

9. In-order Traversal
Example:
Solution: 4 2 5 1 3

10. In-order Traversal
T
r
b c
d e
g
f
k
h i j
Algorithm: In-order traversal
Procedure In-order (T: ordered rooted tree)
r := root of T
If r is a leaf then list r
else
begin
l := first child of from left to right
T (l) := subtree with l as its root
In-order( T(l))
list r
for each child c of r except for l from left to right
T ( c):= subtree with c as its root
In-order(T(c))
end

11. Post-order Traversal
 In this traversal method, the root node is visited last,
hence the name. First we traverse the left subtree,
then the right subtree and finally the root node.
In-order traversal
1. Visit all the nodes in the left subtree
2. Visit all the nodes in the right subtree
3. Visit root node

12. Post-order Traversal
Example:
Solution: 4 5 2 3 1

13. Pre-order Traversal
T
r
b c
d e
g
f
k
h i j
Algorithm: Post-order traversal
Procedure post-order(T : ordered rooted tree)
r :=root of T
For each child c of r from left to right
Begin
T(c) := subtree with c as its root
Post-order (T(c))
end
List r

14. Thank you