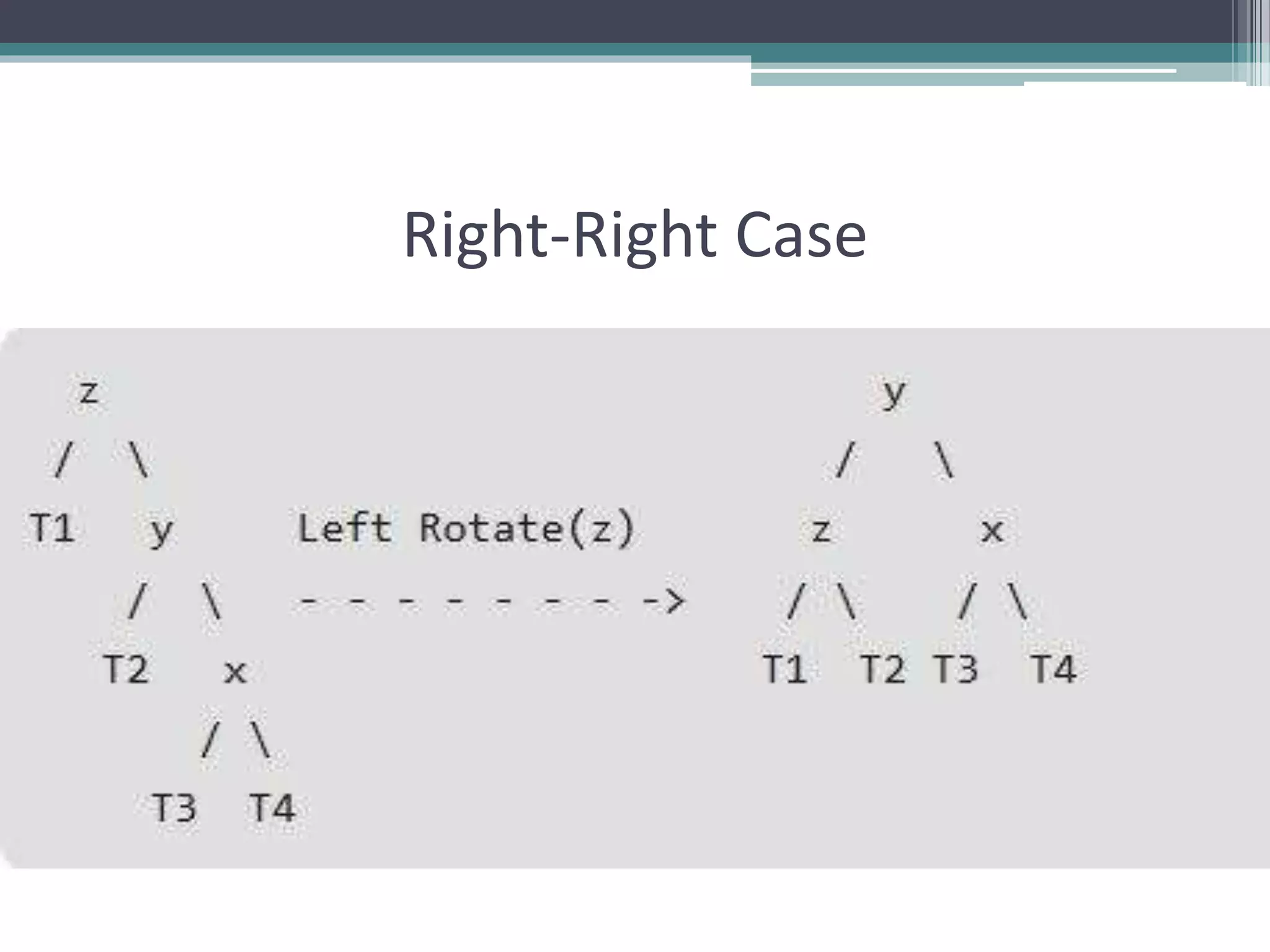
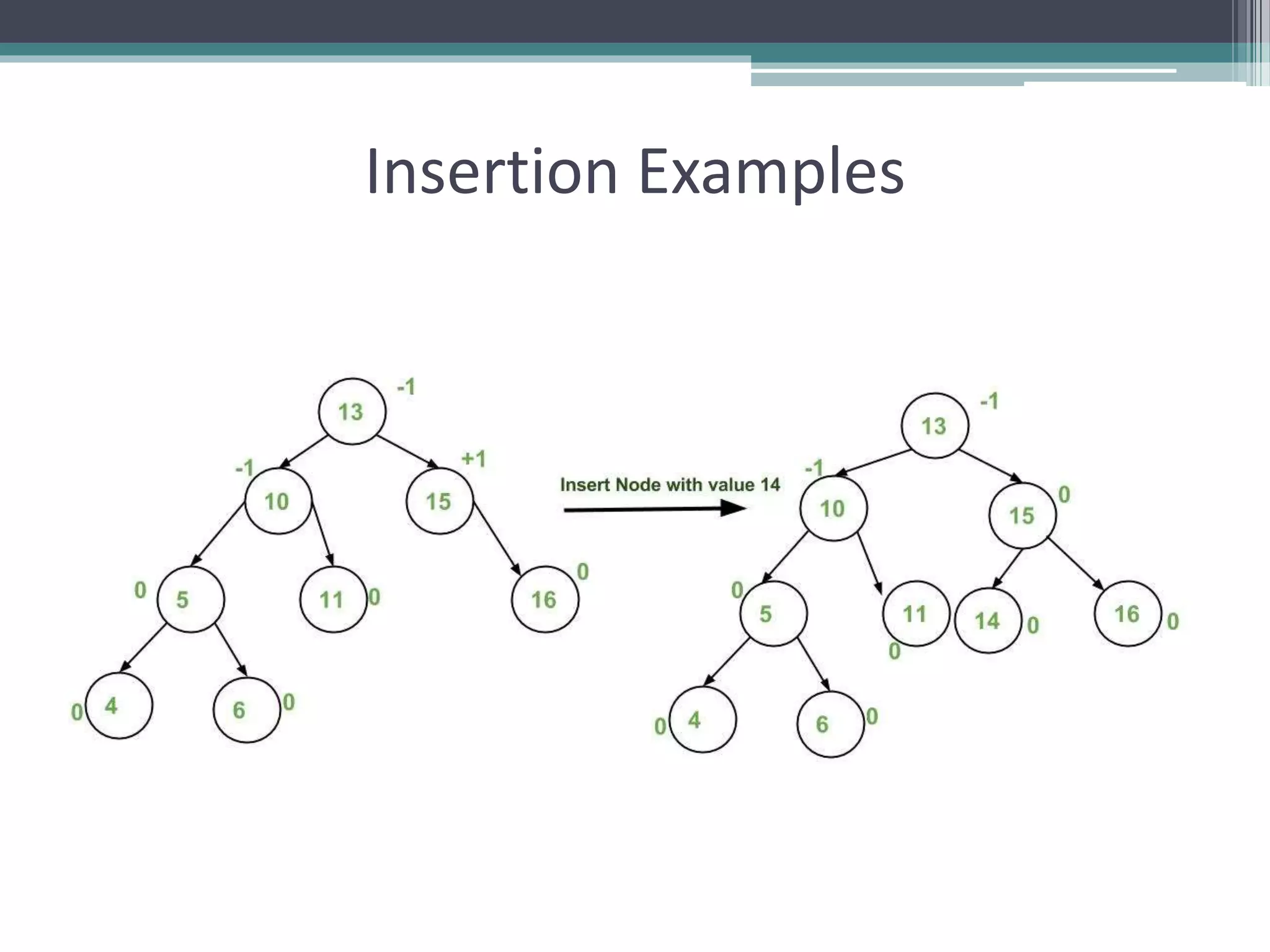
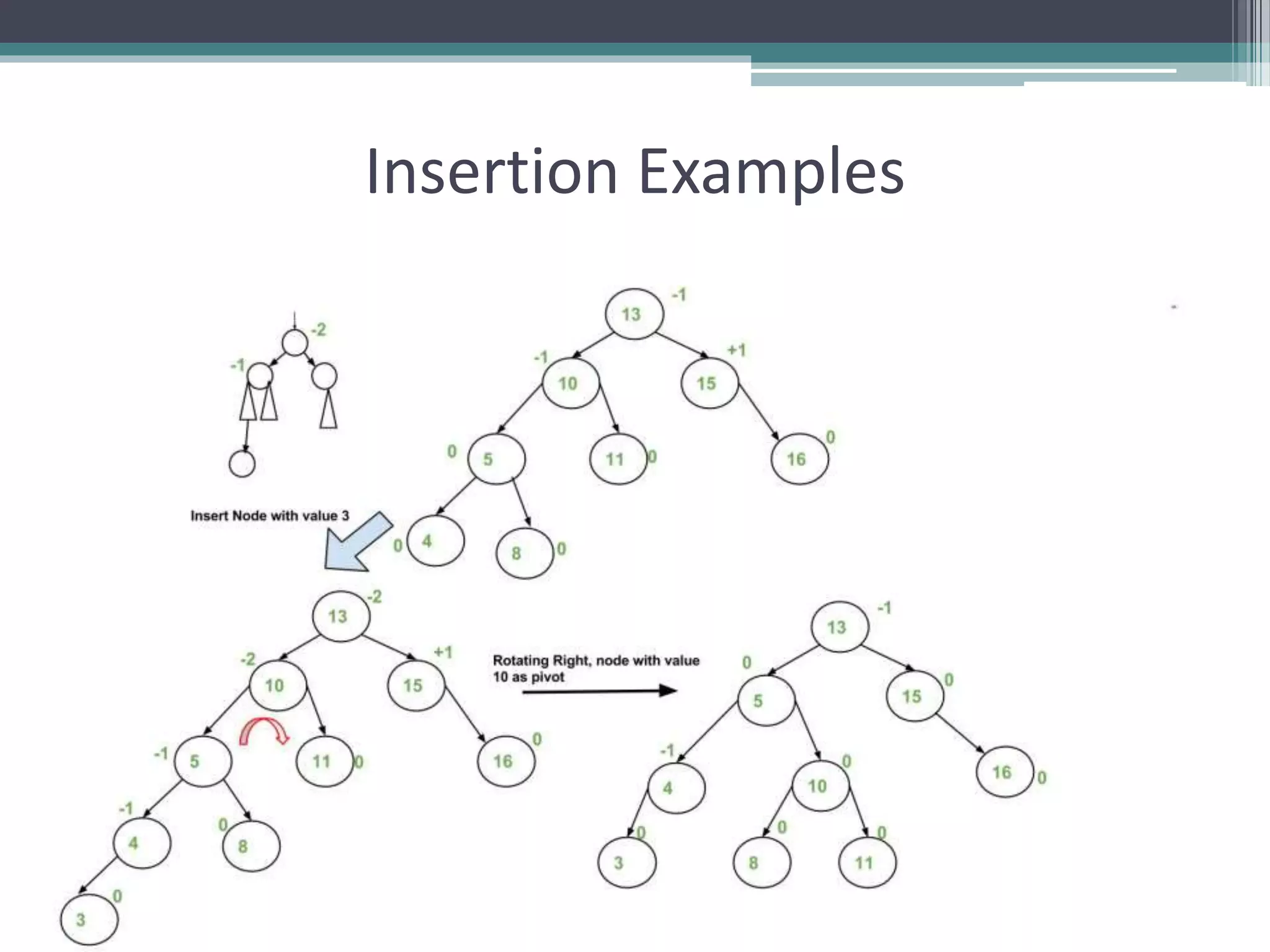
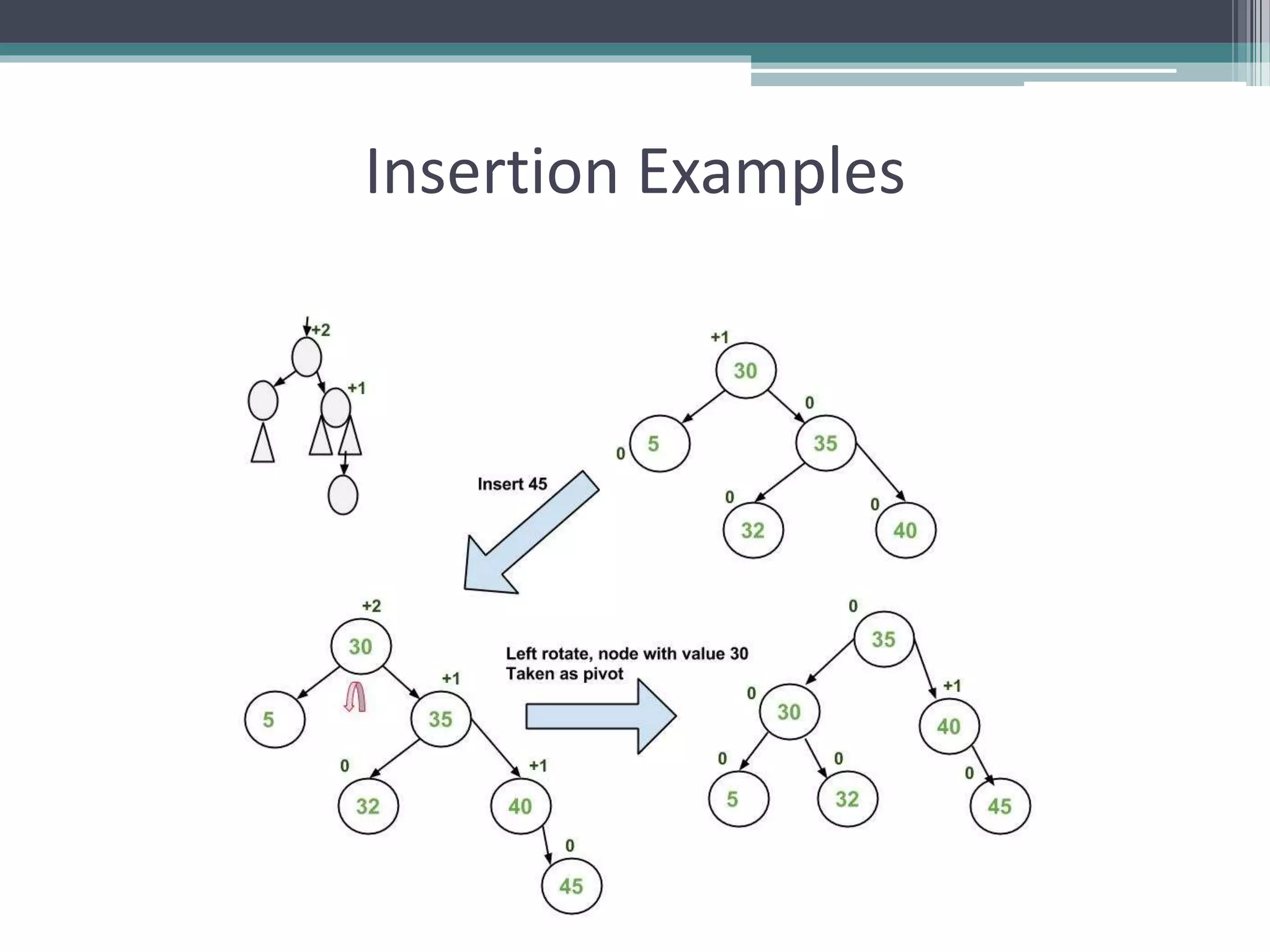
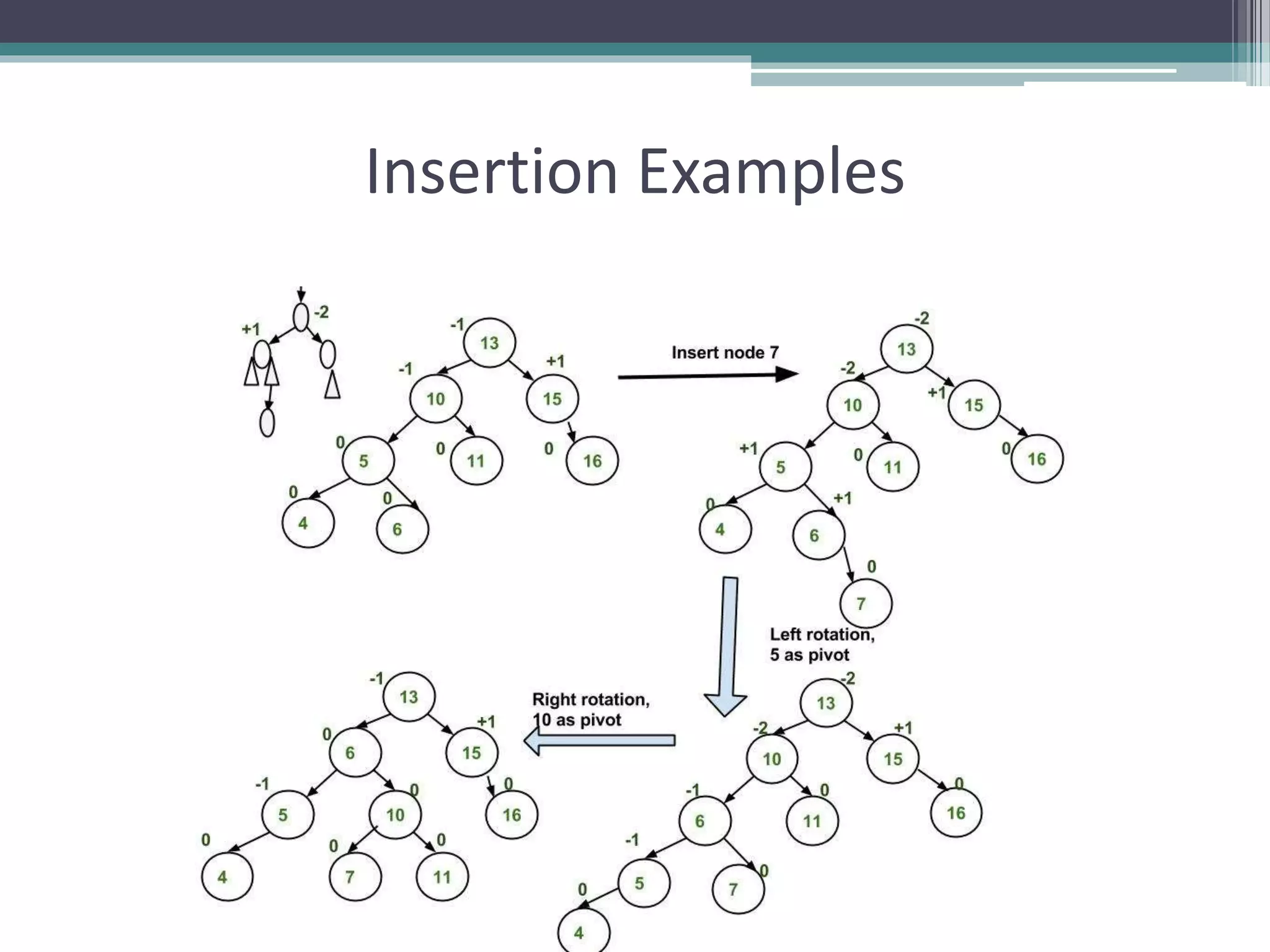
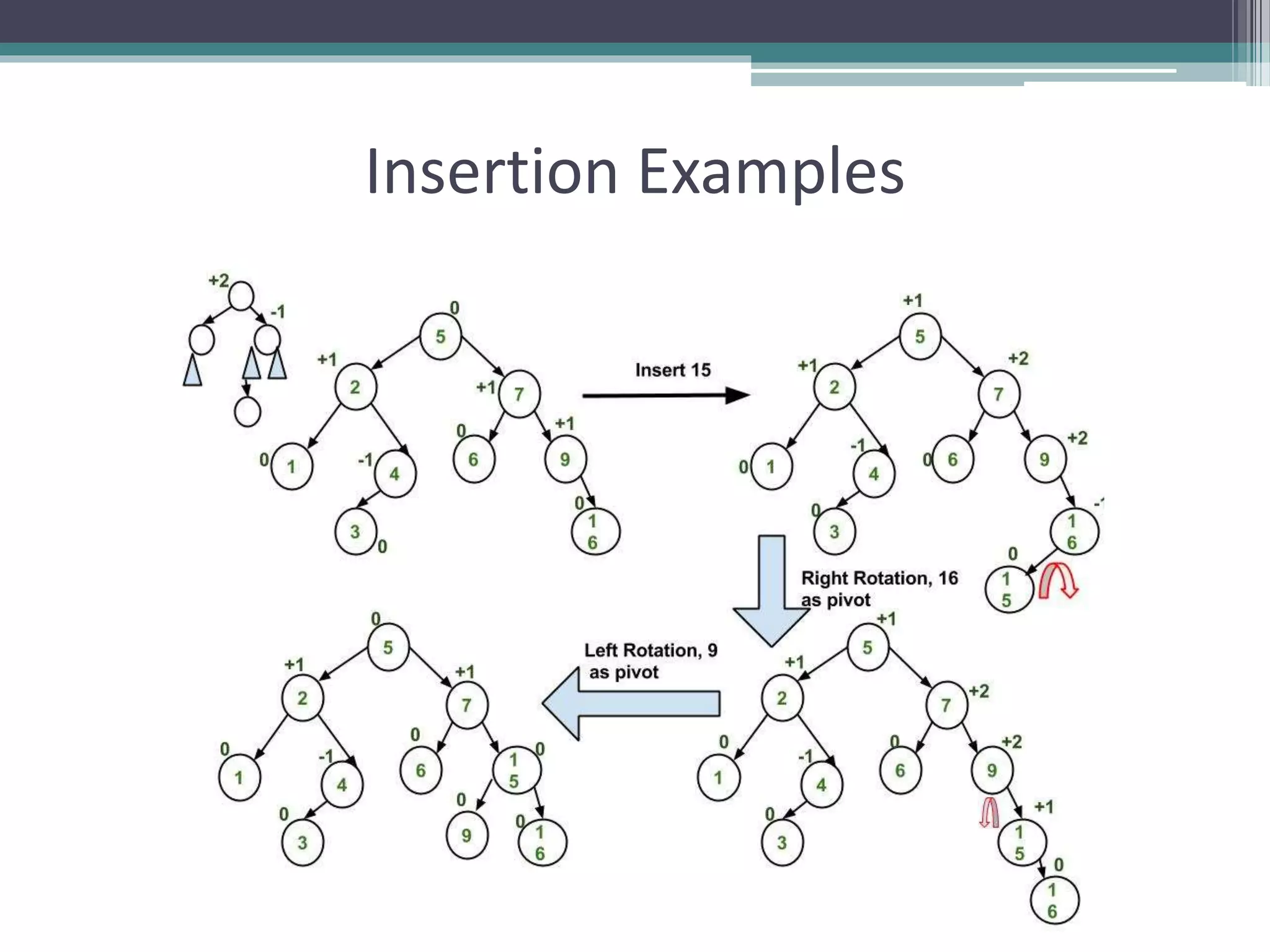
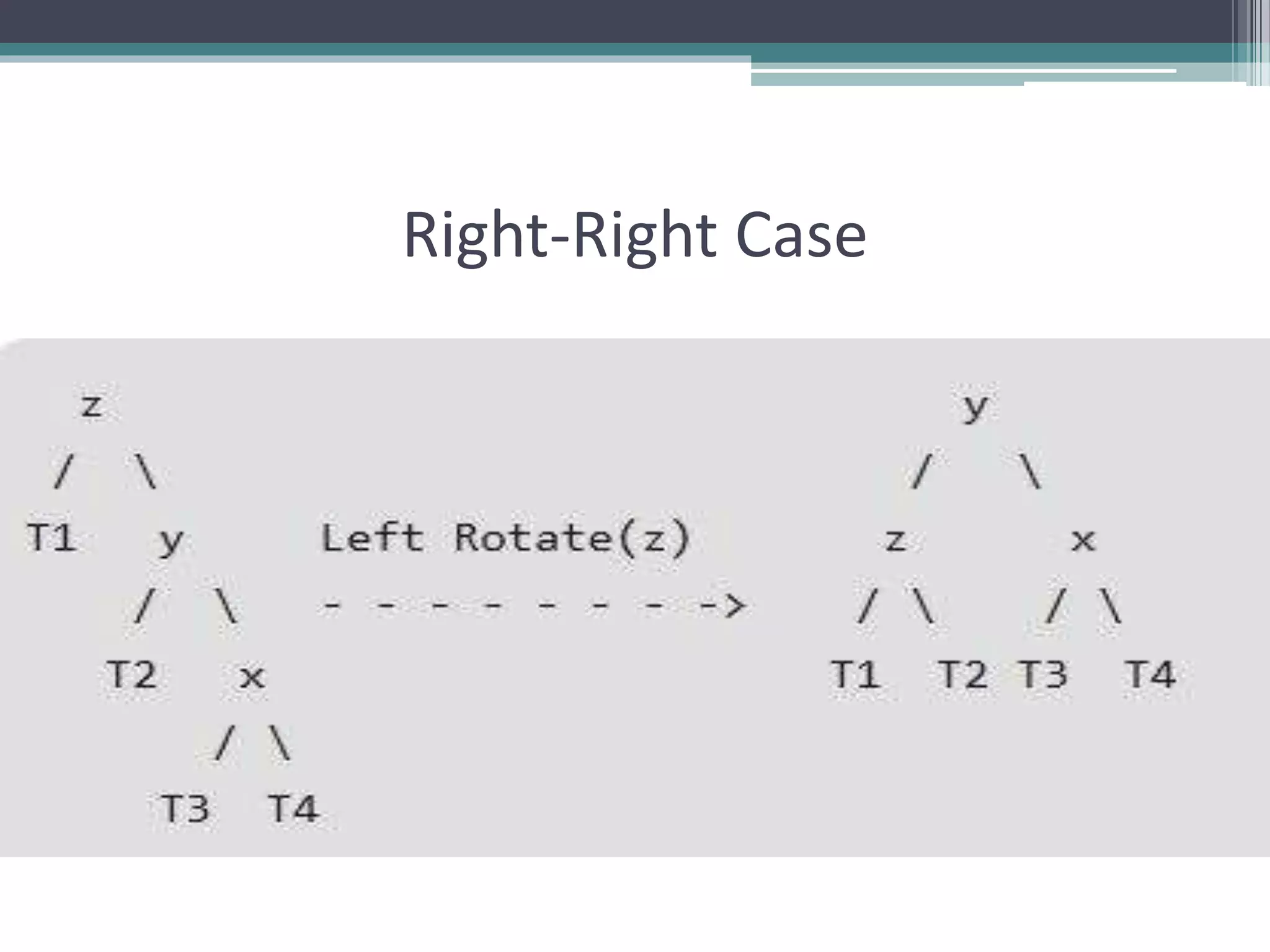
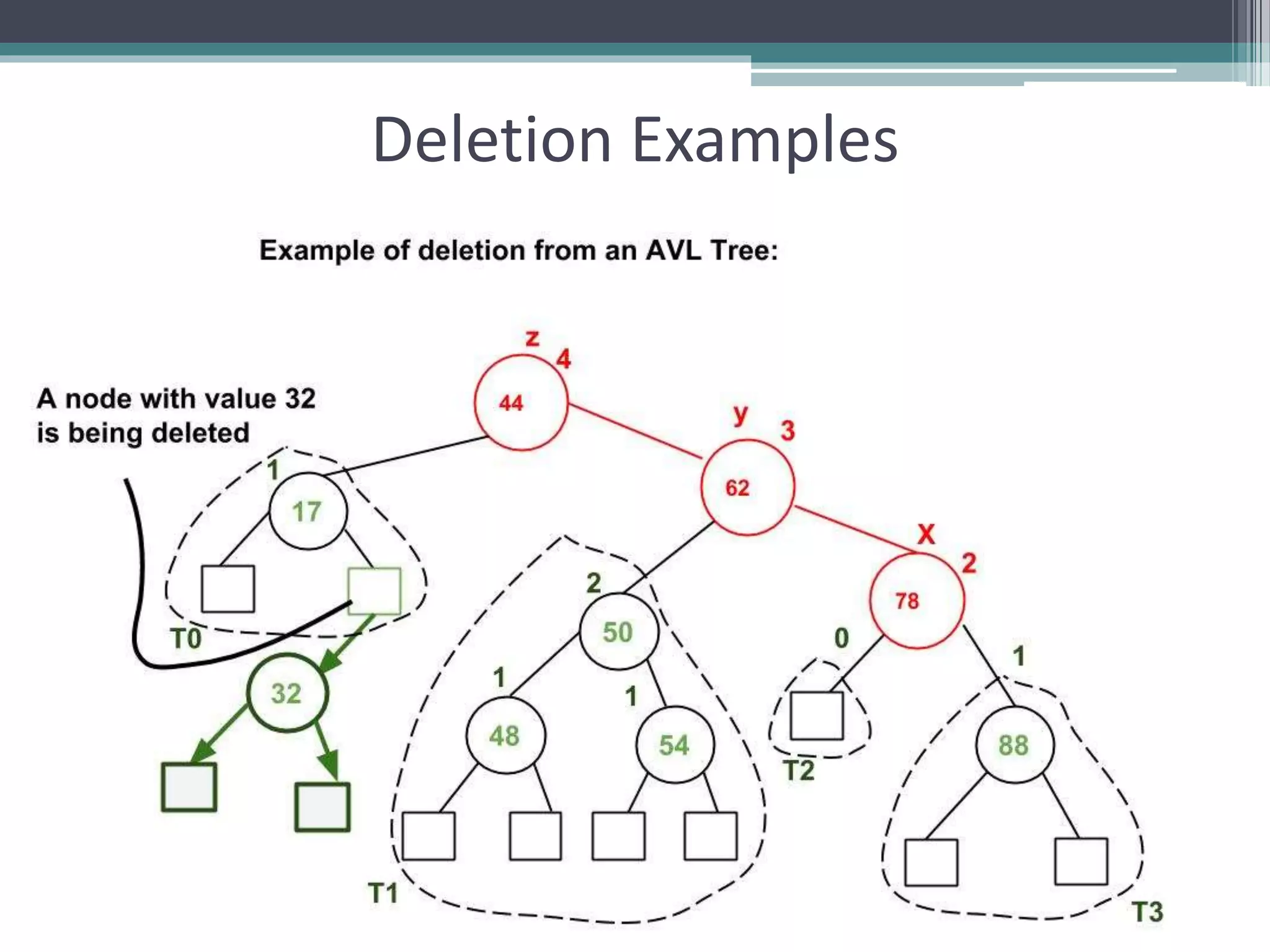
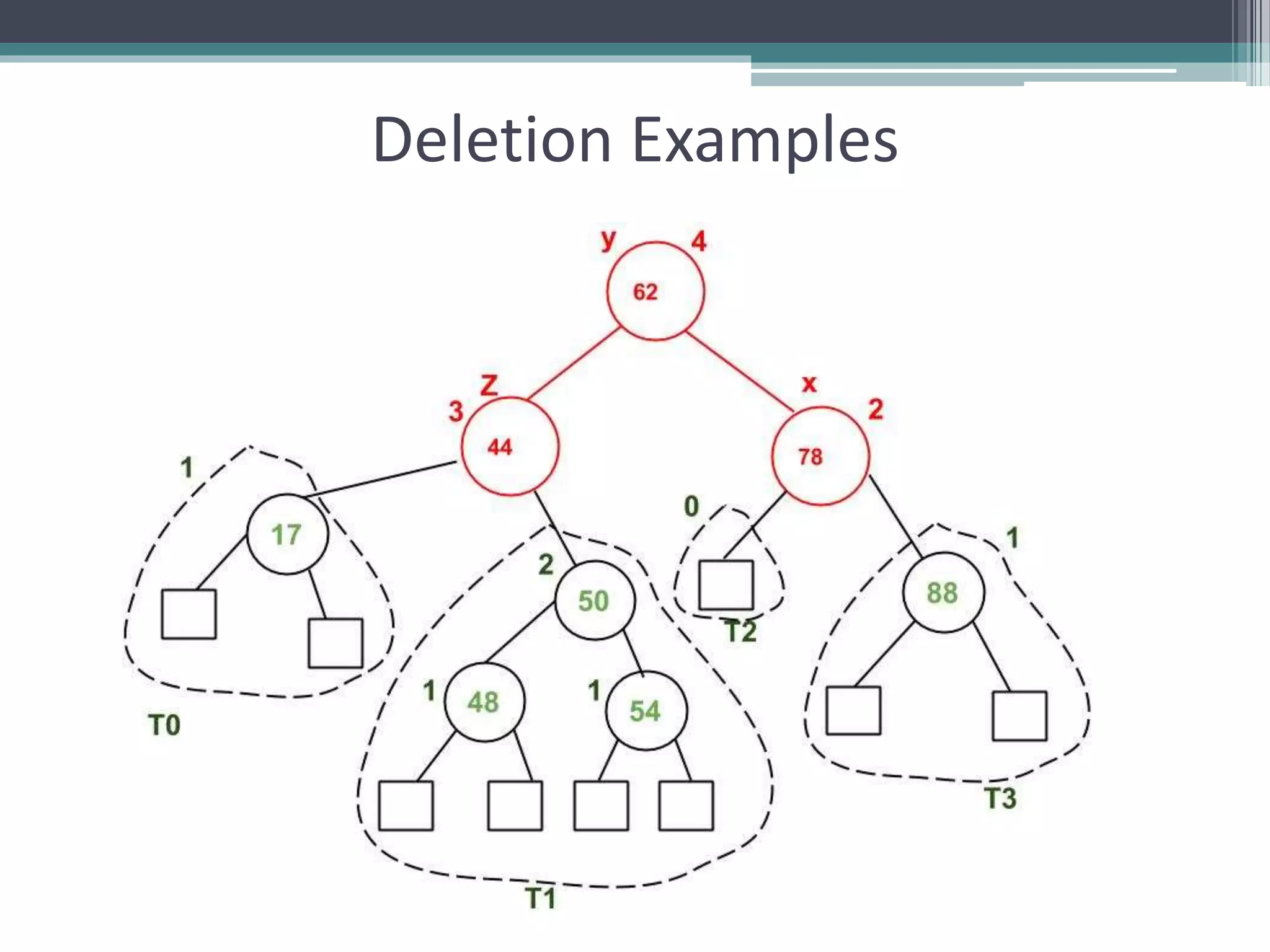
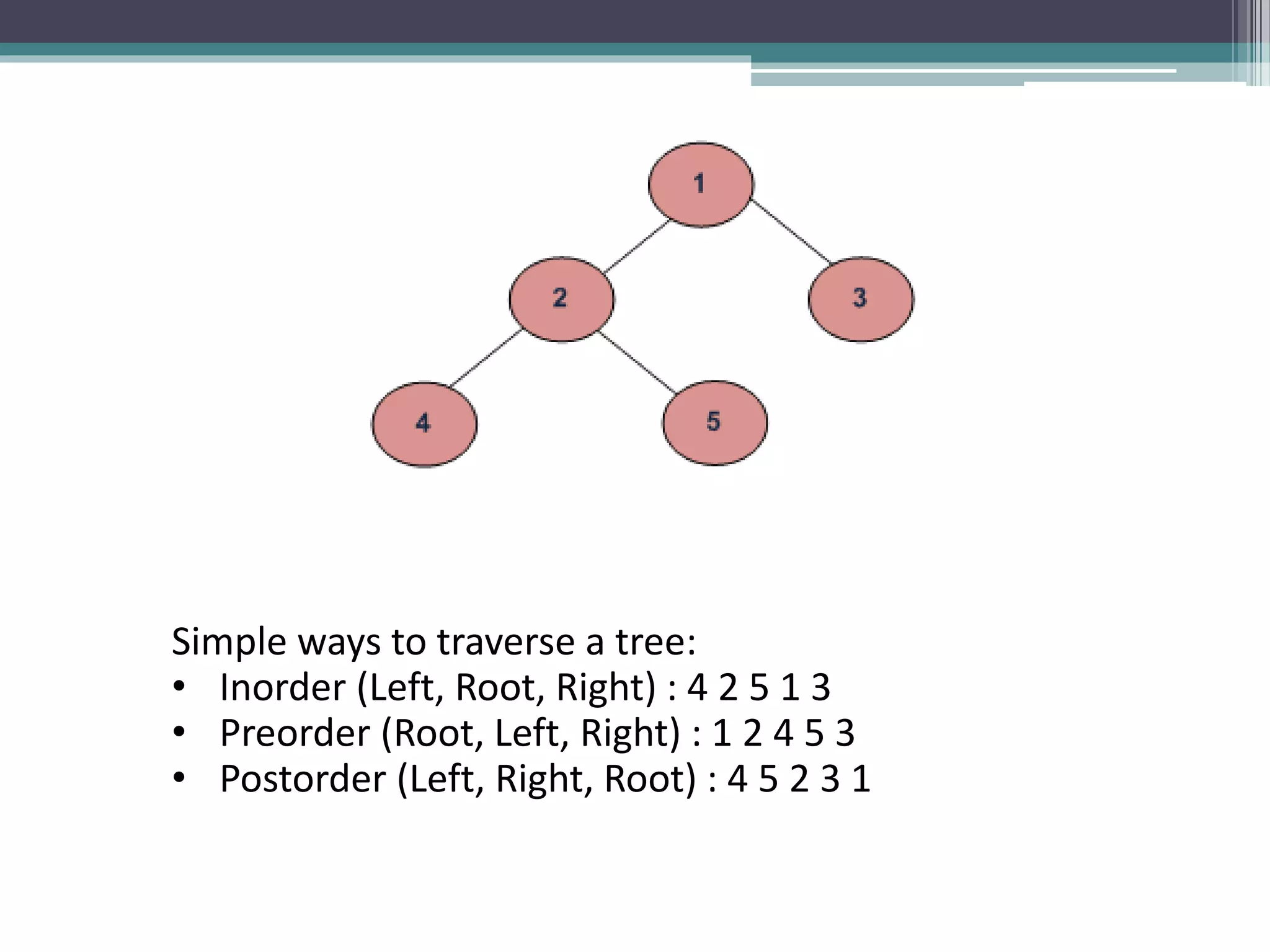
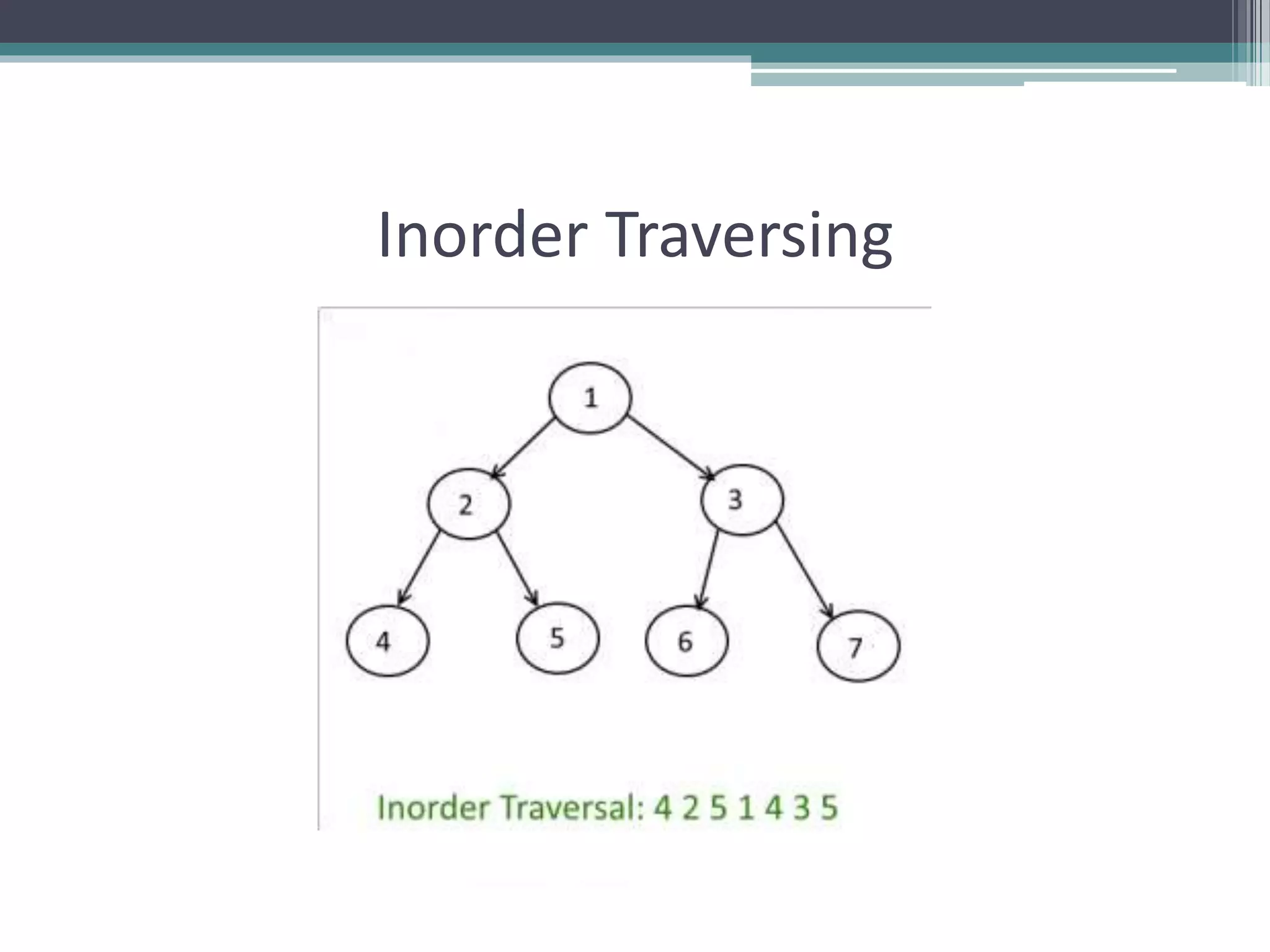
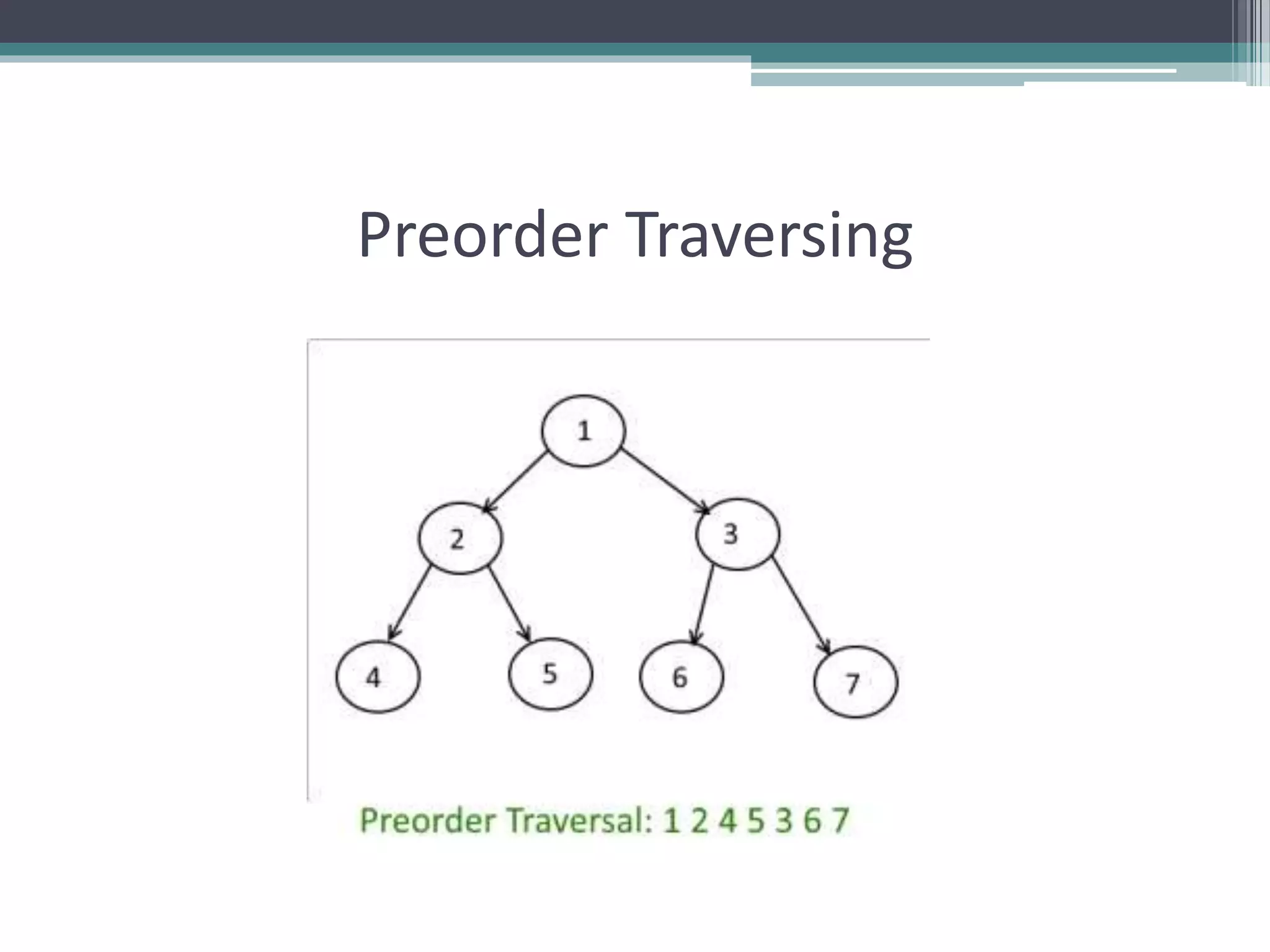
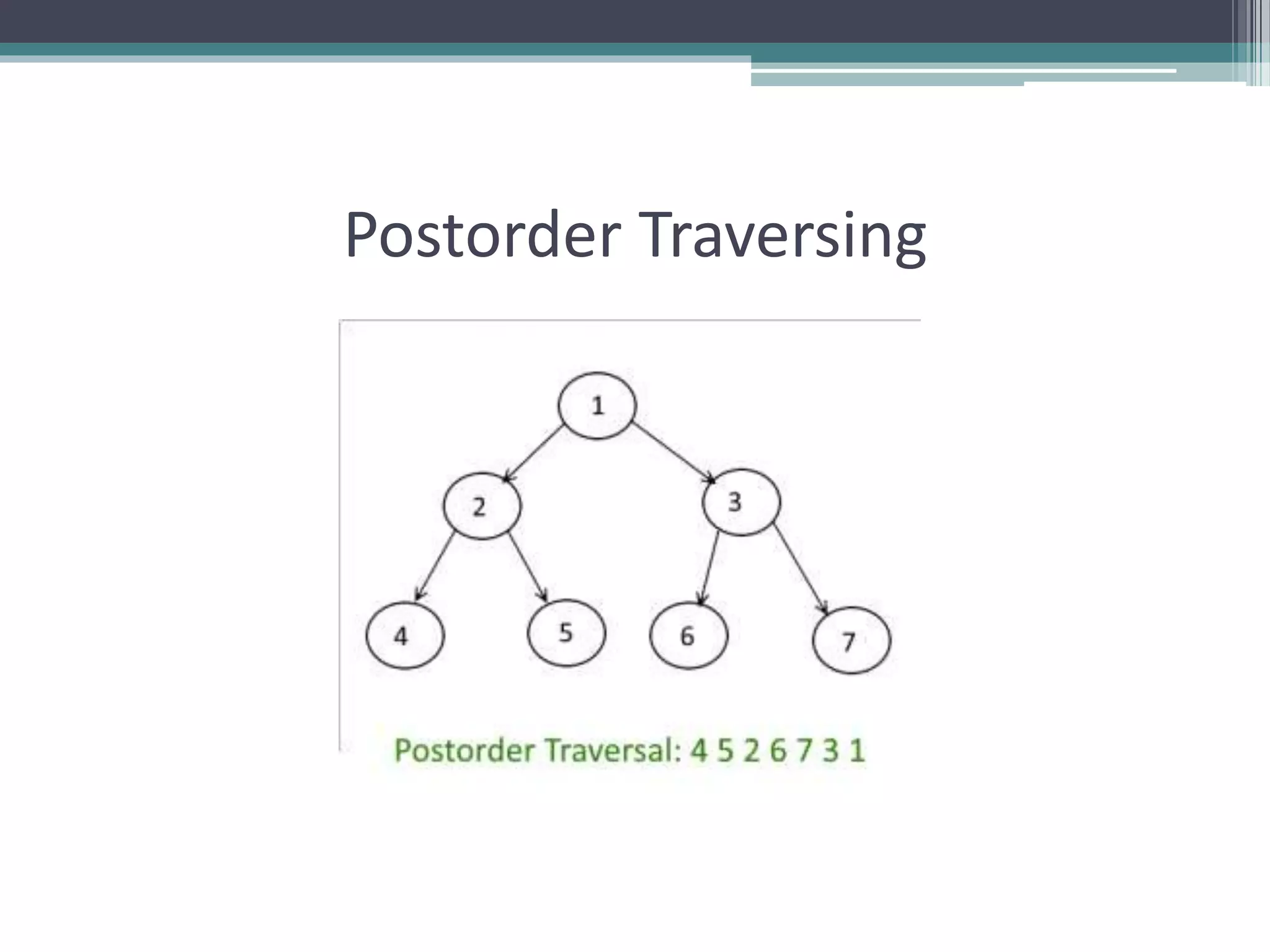
The document provides a comprehensive overview of AVL trees, which are self-balancing binary search trees ensuring that the height difference between left and right subtrees does not exceed one. It details the operations of insertion and deletion, including the necessary rebalancing through rotations, as well as traversal methods like in-order, pre-order, and post-order. The document also discusses time complexities associated with various operations within AVL trees, emphasizing their efficiency compared to unbalanced binary search trees.