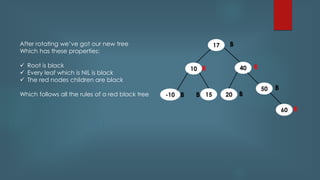
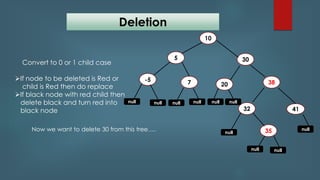
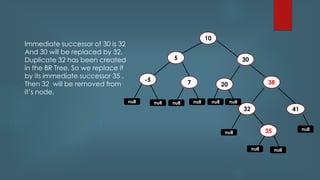
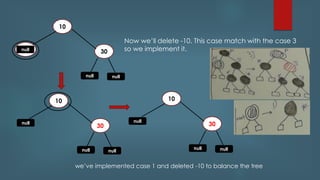
This document discusses Red Black Trees. It provides information on the structure and properties of Red Black Trees including that every node is red or black, the root is black, and red nodes have black children. It describes the rules for insertion, deletion, and rebalancing including recoloring nodes and performing rotations. It notes that search, insert, and delete operations on a Red Black Tree have time complexities of O(log n) on average and worst case due to the self-balancing nature of Red Black Trees.

1. TOPIC: RED BLACK TREE
MEMBERS NAME ID
1. Sazidur Rahman Bhuiyan 1511672042
2. MD. Nurul Alam 1511971042
3. Md. Monir Hossain 1521507042

2. RED BLACK TREE

3.  1. Every node is either red or black .
 2. The root is black
 3. If a node is red, then both its children are black
 4. For each node, all path from the root to descendant leaves
contain the same number of black nodes.
Rules of Red Black TREE

4.  1.New Node Must be Red.
 2.Arrange Color according to RBT properties:
(i)Root is always black.
(ii)Every leaf which is Nil is black.
(iii)If the node is red then its both children must be black
(iv) No red-red parent-child relation
Insertion

5. If (empty)Black Node
else
create red leaf node
if (parent is black )done
else
If (parent sibling is red)
if (parent’s parent is root)
recolor ;
Else recolor & recheck
Else
{
rotate
if (LL)rotate right
if (LR)rotate right->left
if (RL)rotate left ->right
If (RR)rotate left
}
Algorithm of Insertion

6. 10
-10 17
40
50
15
20
60
B
B
BB
R
R R
R
 We’ve inserted 60 in the tree and here
red-red situation occurred.
For this we have to check sibling color.
Here it’s red and so that we have to do re-coloring
the tree to make it balanced by color.
Insertion Example

7. 10
-10 17
40
50
15
20
60
B
B
RB
R
B B
R
 Again red-red situation occurred and
sibling is black.
So we have to make rotation. As it’s a
Right-right situation, we have to do left rotation
left rotation

8. 17
40
50
20
60
RR
B
B
B
R
10
-10 B 15B
After rotating we’ve got our new tree
Which has these properties:
 Root is black
 Every leaf which is NIL is black
 The red nodes children are black
Which follows all the rules of a red black tree

9. Convert to 0 or 1 child case
If node to be deleted is Red or
child is Red then do replace
If black node with red child then
delete black and turn red into
black node
10
5 30
-5 7 3820
4132
35Now we want to delete 30 from this tree….
null null nullnull null null
null
null null
null
Deletion

10. 10
5 30
-5 7 3820
4132
null null nullnull null null
null
null
32
Immediate successor of 30 is 32
And 30 will be replaced by 32.
Duplicate 32 has been created
in the BR Tree. So we replace it
by its immediate successor 35 .
Then 32 will be removed from
it’s node.
35
null null
35

11. 10
5 32
-5 7 3820
4135
null null nullnull null null
null null
null
Here the color of the node 35
has been changed to black.
After the deletion process we get
a perfect balanced tree.
 Here every path contains same
Number of black nodes.

12. Double black node has six cases
10
-10 30
nullnullnull null

13. 10
30
nullnull
null
Now we’ll delete -10. This case match with the case 3
so we implement it.
10
30
nullnull
null
we’ve implemented case 1 and deleted -10 to balance the tree
10
30
nullnull
null

14. Fig: Example of an worst case RB Tree
6
3
*Length of the smallest path = 3
*Length of the longest path = 6
 Length of the longest path of a RBT is not more than the
double length of the shortest path. That’s why the run time
complexity of search ,insert and delete always remains
O(log N).
*No red-red parent child.
*Same number of black nodes in all paths.
Time Complexity

15.  The tree height is always O(log n); where n is the number
of node in the tree.
 Searching for a node in a balanced tree takes O(log n)
time.
 Similarly adding and removing aslo take O(log n) time.
CASE AVERAGE WORST
Insertion O(log (n)) O(log (n))
Deletion O(log (n)) O(log (n))
Search O(log (n)) O(log (n))

16.  Red-black trees are self-balancing so these operations are
guaranteed to be O(log(n)); a simple binary search tree, on the
other hand, could potentially become unbalanced, degrading to
O(n) performance for Insert, Delete, and Get. Particularly useful
when inserts and/or deletes are relatively frequent. Relatively low
constants in a wide variety of scenarios. All the advantages of
binary search trees.
Benefits of RBT