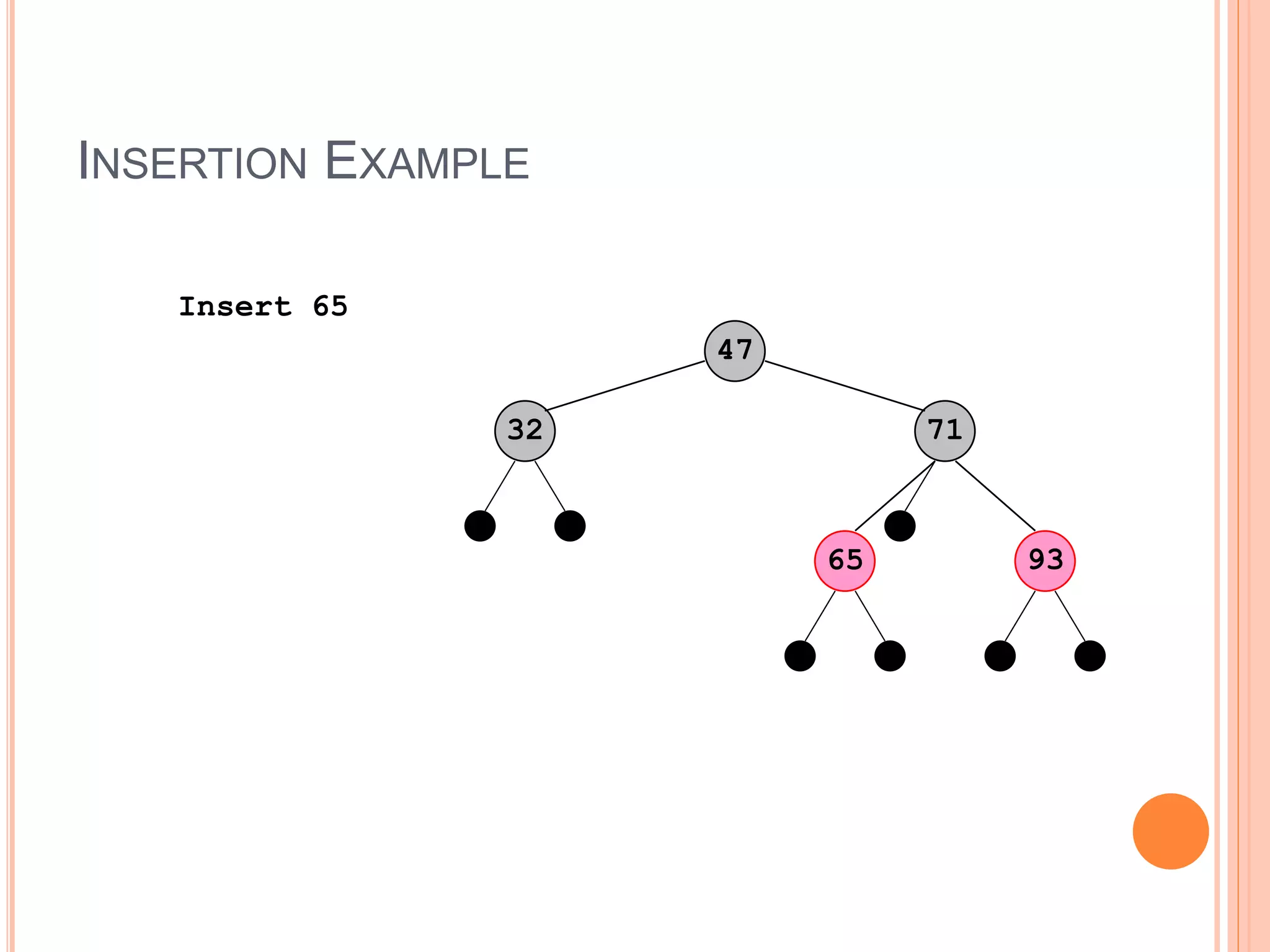
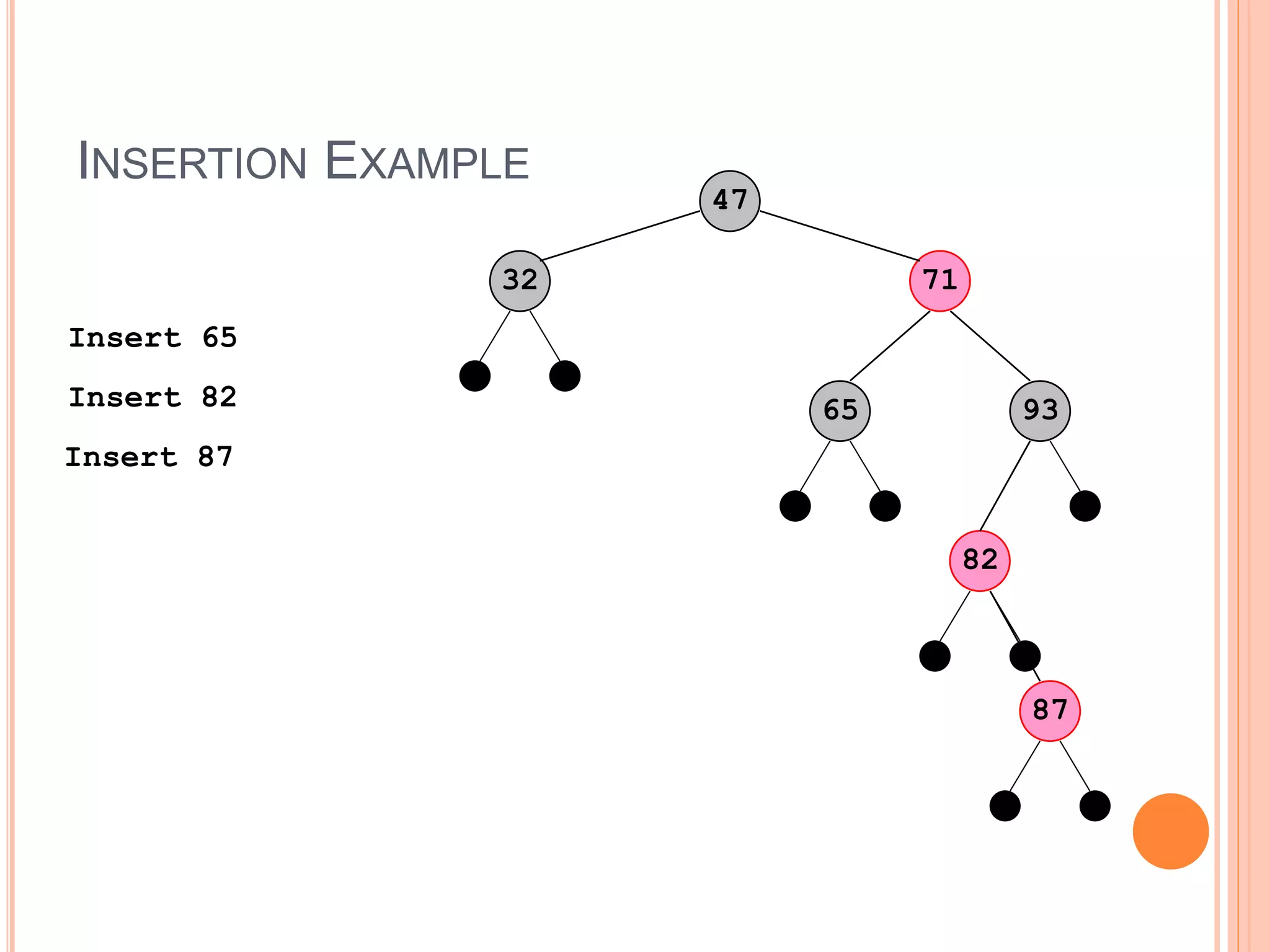
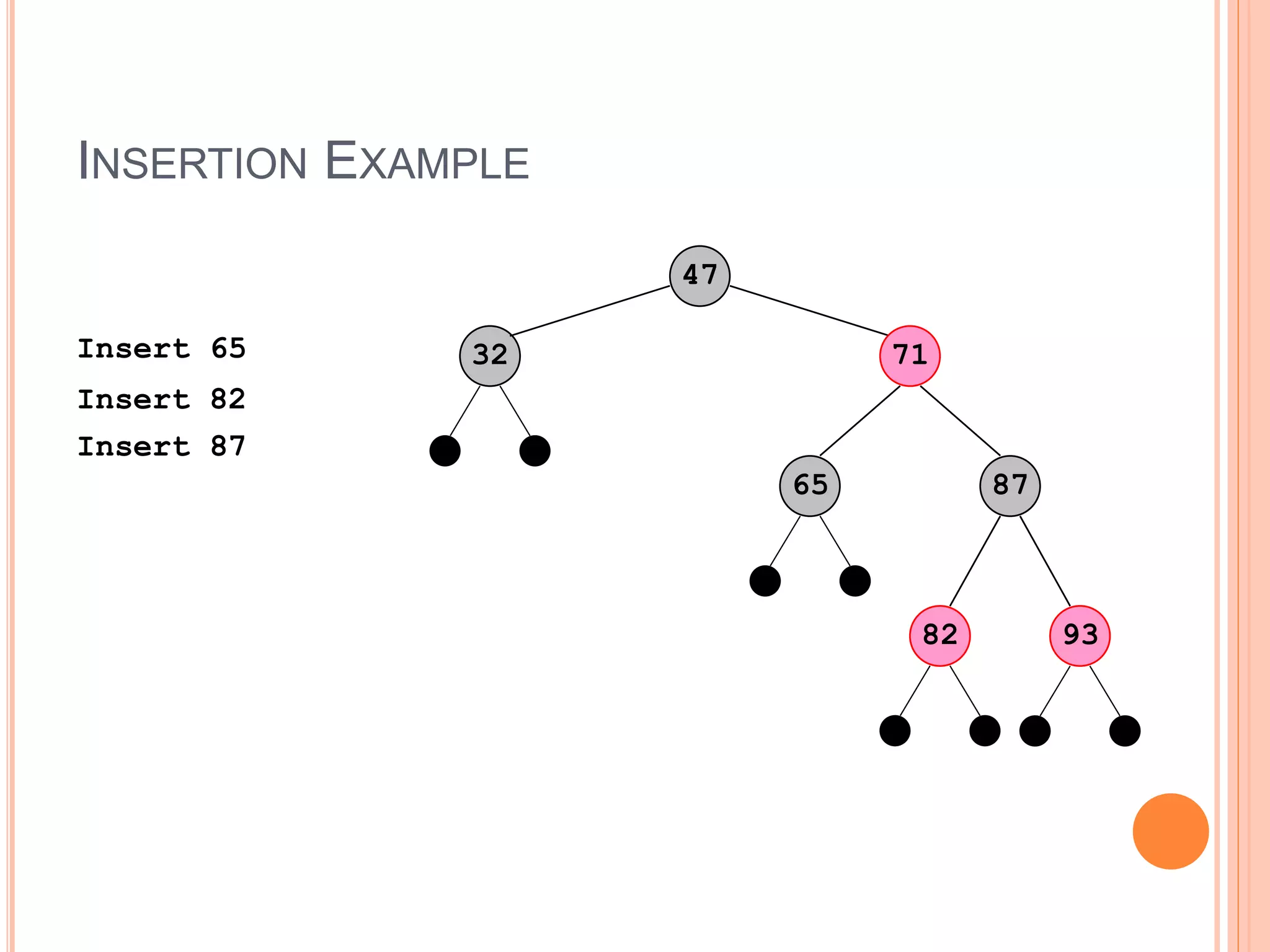
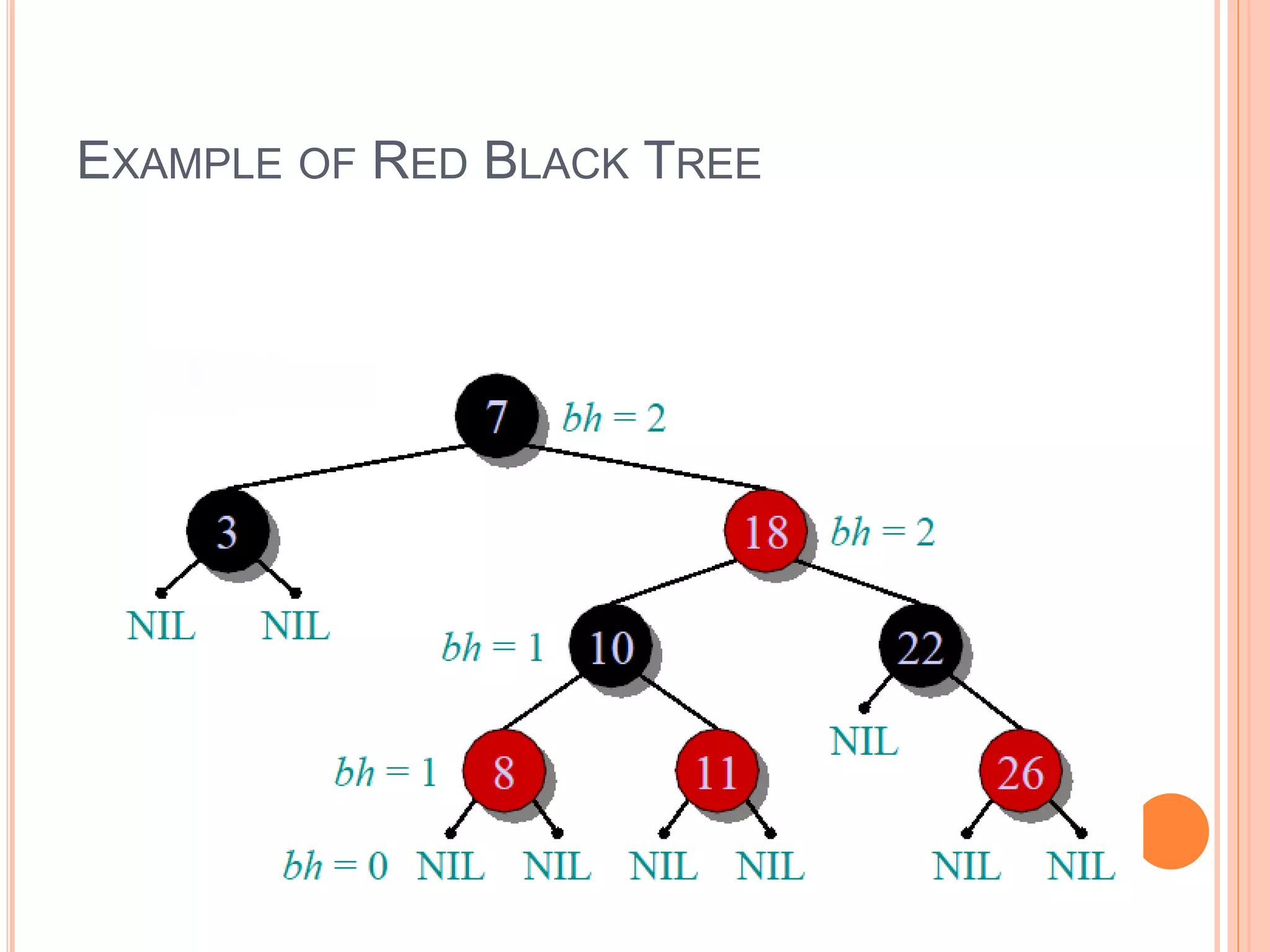
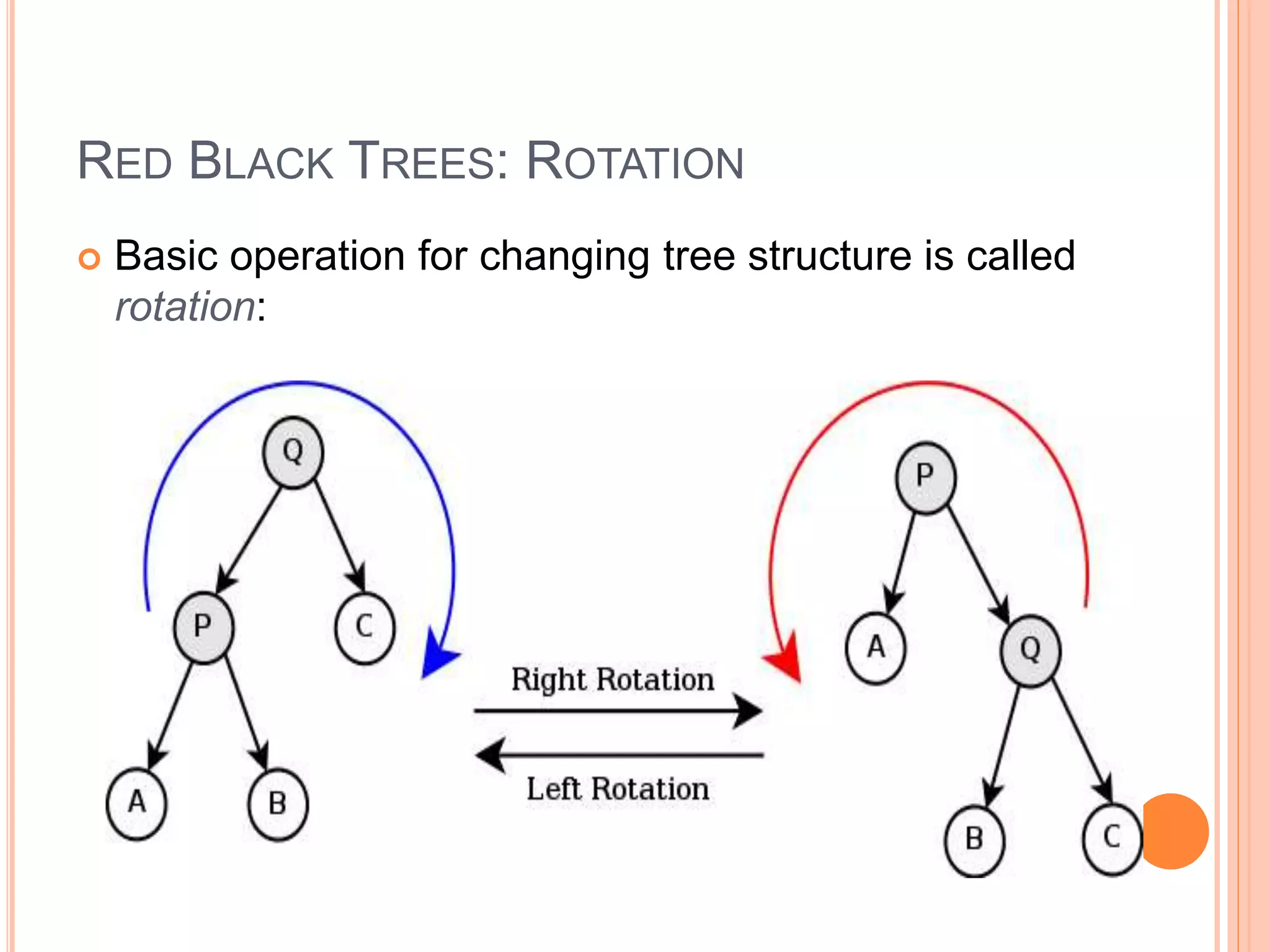
A red-black tree is a self-balancing binary search tree where each node is colored red or black. It provides logarithmic time bounds for search, insert, and delete operations. It achieves self-balancing by restricting the number of red nodes along any path, ensuring that no path is more than twice as long as any other path. Rotations are used during insertion and deletion operations to rebalance the tree and maintain these properties.

1. RED-BLACK TREE

2. INTRODUCTION
 A balancing binary search tree.
 A data structure requires an extra one bit color field
in each node which is red or black.
 Leonidas J. Guibas and Robert Sedgewick derived
the red-black tree from the symmetric binary B-tree.

3. EXAMPLE OF RED BLACK TREE

4. PROPERTIES OF RED BLACK TREE
 The root and leaves (NIL’s) are black.
 A RED parent never has a RED child.
 in other words: there are never two successive RED nodes in
a path
 Every path from the root to an empty subtree contains the same
number of BLACK nodes
 called the black height
 We can use black height to measure the balance of a red-black
tree.

5. RED BLACK TREE OPERATIONS
Average
Space O(n)
Search
O(log2 n)
Traversal *O(n)
Insertion
O(log2 n)
Deletion
O(log2 n)

6. RED BLACK TREES: ROTATION
 Basic operation for changing tree structure is called
rotation:

7. RB TREES: ROTATION
x
y
y
x
 A lot of pointer manipulation
 x keeps its left child
 y keeps its right child
 x’s right child becomes y’s left child
 x’s and y’s parents change
A B
C A
B C

8. ROTATION ALGORITHM
LEFT-ROTATE(T, x)
y ← x->right
x->right← y->left
y->left->p ← x
y->p ← x->p
if x->p = Null
then T->root ← y
else if x = x->p->left
then x->p->left ← y
else x->p->right ← y
y->left ← x
x->p ← y
RIGHT-ROTATE(T, x)
y ← x->left
x->left← y->right
y->right->p ← x
y->p ← x->p
if x->p = Null
then T->root ← y
else if x = x->p->right
then x->p->right ← y
else x->p->left ← y
y->right ← x
x->p ← y
Runtime : O(1) for Both.

9. ROTATION EXAMPLE
 Rotate left about 9:
12
5 9
7
8
11

10. ROTATION EXAMPLE
 Rotate left about 9:
5 12
7
9
118

11. RED-BLACK TREES: INSERTION
 Insertion: the basic idea
 Insert x into tree, color x red
 Only r-b property 3 might be violated (if p[x] red)
 If so, move violation up tree until a place is found where it can
be fixed
 Total time will be O(log n)

12. Insertion Algorithm
TreeNode<T> rbInsert(TreeNode<T> root,TreeNode<T> x)// returns a new root
{
root=bstInsert(root,x); // a modification of BST insertItem
x.setColor(red);
while (x != root and x.getParent().getColor() == red) {
if (x.getParent() == x.getParent().getParent().getLeft()) {
//parent is left child
y = x.getParent().getParent().getRight() //uncle of x
if (y.getColor() == red) {// uncle is red
x.getParent().setColor(black);
y.setColor(black);
x.getParent().getParent().setColor(red);
x = x.getParent().getParent();
} else { // uncle is black
if (x == x.getParent().getRight()) {
x = x.getParent();
root = left_rotate(root,x);
}
x.getParent().setColor(black);
x.getParent().getParent().setColor(red);
root = right_rotate(root,x.getParent().getParent());
}}
} else
// ... symmetric to if
} // end while
root.setColor(black);
return root;
}

13. RB INSERT: CASE 1
B
 
x
● Case 1: “uncle” is red
● In figures below, all ’s are
equal-black-height
subtrees
C
A D
  
C
A D
 
y
new x
Same action whether x is a left or a right child
B
 
x
case 1

14. RB INSERT: CASE 2
B
 
x
● Case 2:
■ “Uncle” is black
■ Node x is a right child
● Transform to case 3 via a left-rotation
C
A 
C
By
A
 
x 
case 2

y
Transform case 2 into case 3 (x is left child) with a left rotation
This preserves property 4: all downward paths contain same number of black nodes

15. RB INSERT: CASE 3
● Case 3:
■ “Uncle” is black
■ Node x is a left child
● Change colors; rotate right
B
Ax

case 3
C
B
A
 
x 
y C
 
Perform some color changes and do a right rotation
Again, preserves property 4: all downward paths contain same number of black nodes

16. RB INSERT: CASES 4-6
 Cases 1-3 hold if x’s parent is a left child
 If x’s parent is a right child, cases 4-6 are symmetric
(swap left for right)

17. INSERTION EXAMPLE
Insert 65
47
7132
93

18. INSERTION EXAMPLE
Insert 65
47
7132
65 93

19. INSERTION EXAMPLE
Insert 65
47
7132
65 93
Insert 82

20. INSERTION EXAMPLE
82
Insert 65 47
7132
65 93
Insert 82

21. INSERTION EXAMPLE
82
Insert 65
47
7132
65 93
Insert 82
65
71
93
change nodes’ colors

22. INSERTION EXAMPLE
9365
71
82
Insert 65
47
32
Insert 82
Insert 87
87

23. INSERTION EXAMPLE
9365
71
82
Insert 65
47
32
Insert 82
Insert 87
87

24. INSERTION EXAMPLE
9365
71
87
Insert 65
47
32
Insert 82
Insert 87
82

25. INSERTION EXAMPLE
9365
87
Insert 65
47
32
Insert 82
Insert 87
82
71
87
93
change nodes’ colors

26. INSERTION EXAMPLE
87
93
65
Insert 65
47
32
Insert 82
Insert 87
82
71

27. RB TREE DELETION ALGORITHM
TreeNode<T> rbDelete(TreeNode<T> root,TreeNode<T> z)
//return new root, z contains item to be deleted
{
TreeNode<T> x,y;
// find node y, which is going to be removed
if (z.getLeft() == null || z.getRight() == null)
y = z;
else {
y = successor(z); // or predecessor
z.setItem(y.getItem); // move data from y to z
}
// find child x of y
if (y.getRight() != null)
x = y.getRight();
else
x = y.getLeft();
// Note x might be null; create a pretend node
if (x == null) {
x = new TreeNode<T>(null);
x.setColor(black);
}

28. RED-BLACK TREE RETRIEVAL:
 Retrieving a node from a red-black tree doesn’t
require more than the use of the BST procedure,
which takes O(log n) time.

29. RB TREES EFFICIENCY
 All operations work in time O(height)
 and we have proved that heigh is O(log n)
 hence, all operations work in time O(log n)! – much
more efficient than linked list or arrays implementation of
sorted list!

30. RED BLACK TREE APPLICATION
 Completely Fair Scheduler in Linux Kernel.
 Computational Geometry Data structures.
 Red-black trees make less structural changes to balance
themselves .
 To keep track of the virtual memory segments for a process -
the start address of the range serves as the key.
 Red–black trees are also particularly valuable in functional
programming
To keep track of the virtual memory segments for a process - the
start address of the range serves as the key.

31. COMPARISON BETWEEN AVL AND RB TREE
 For small data:
 insert: RB tree & avl tree has constant number of max
rotation but RB tree will be faster because on average
RB tree use less rotation.
 lookup: AVL tree is faster, because AVL tree has less
depth.
 delete: RB tree has constant number of max rotation but
AVL tree can have O(log N) times of rotation as worst.
and on average RB tree also has less number of
rotation thus RB tree is faster.

32. COMPARISON BETWEEN AVL AND RB TREE
(CONTINUED)
 for large data:
 insert: AVL tree is faster. because you need to lookup for a
particular node before insertion. as you have more data the time
difference on looking up the particular node grows proportional to
O(log N). but AVL tree & RB tree still only need constant number
of rotation at the worst case. Thus the bottle neck will become
the time you lookup for that particular node.
 lookup: AVL tree is faster. (same as in small data case)
 delete: AVL tree is faster on average, but in worst case RB tree is
faster. because you also need to lookup for a very deep node to
swap before removal (similar to the reason of insertion). on
average both trees has constant number of rotation. but RB tree
has a constant upper bound for rotation.

33. Thank
You