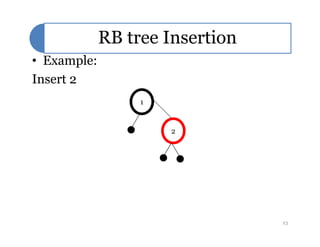
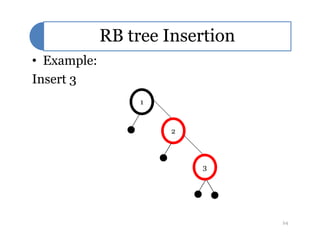
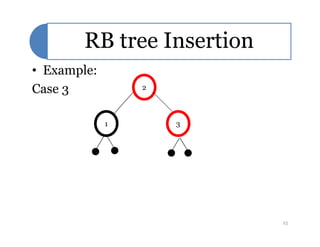
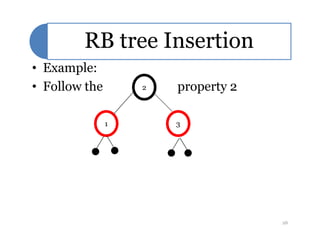
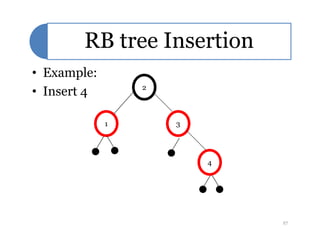
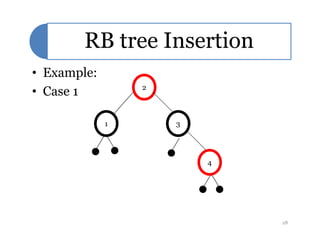
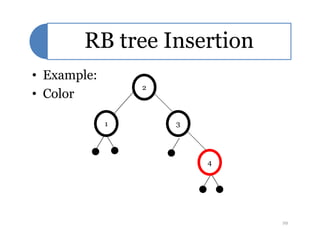
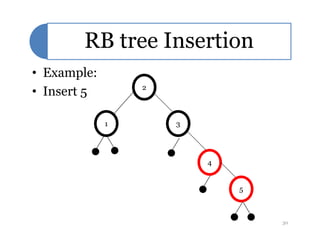
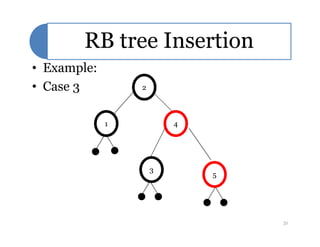
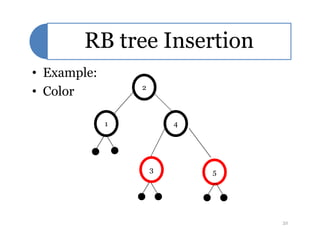
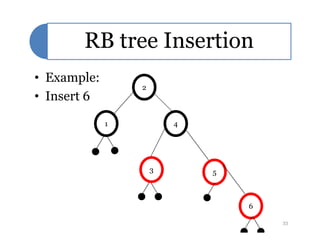
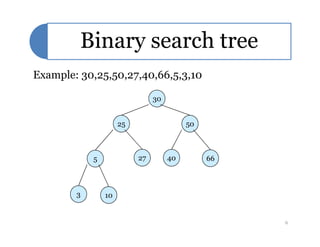
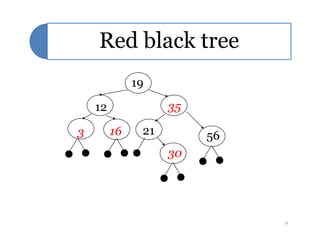
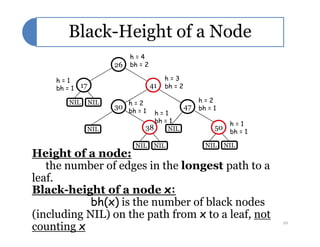
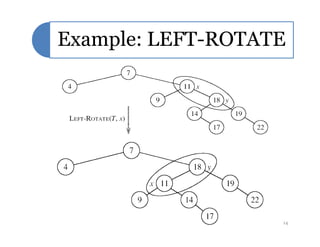
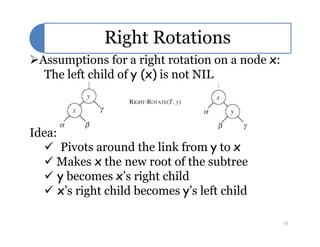
Red-black trees are a self-balancing binary search tree data structure. They follow several properties including: 1) every node is either red or black, 2) the root is black, 3) every leaf node is black, 4) if a node is red then both its children are black, and 5) for each node, all simple paths from the node to descendant leaf nodes contain the same number of black nodes. Rotations are used to maintain these properties during insertions and deletions. Inserting a new node involves finding the appropriate position and may require recoloring nodes and performing rotations to ensure the red-black tree properties are satisfied. Insertion takes O(log n) time.

1. Red Black TreeRed Black Tree
1

2. Group Member
Balawal Hussain 269
Nasir Shahzad 287
Ali Raza 277
Umair Khan 293
Usman Aslam 299
2

3. Red Black VS BNS Tree
Red black tree are new form of data
structure but inherit similarities from
binary search tree
 for example: red black tree have up to 2 for example: red black tree have up to 2
children per node. They must follow the
binary search tree.
 On left side is smaller than parent.
 On right side is greater than parent.
3

4. 4

5. Binary search tree
• In BST, all left sub-tree element should be
less than root node and all right sub-tree
should be greater than root node, called
BST.BST.
• Parent node should not have more than
two children.
Parent<Right
Parent>left
5

6. Binary search tree
30
25 50
Example: 30,25,50,27,40,66,5,3,10
25 50
5 27 40 66
3 10
6

7. About Red black tree
Invented in Invented byInvented in
1972.
Invented by
Rudolf Bayer
7

8. Red black tree
Red black tree properties:
1-Every node is either red or black.
2-The root is black.
3-Every leaf (NIL) is black.3-Every leaf (NIL) is black.
4-If a node is red, then both its children are
black.
5-For each node, all simple paths from the node
to descendant leaves contain the same
number of black nodes.
8

9. Red black tree
19
12 35
2116 5621
30
3
9

10. Black-Height of a Node
26
17 41
30 47
38 50
NIL NIL
h = 4
bh = 2
h = 3
bh = 2
h = 2
bh = 1
h = 1
h = 1
bh = 1
h = 2
bh = 1 h = 1
bh = 1
38 50NIL
NIL NIL NIL NIL
NIL
h = 1
bh = 1
bh = 1
Height of a node:
the number of edges in the longest path to a
leaf.
Black-height of a node x:
bh(x) is the number of black nodes
(including NIL) on the path from x to a leaf, not
counting x
10

11. ROTATIONSROTATIONS
11

12. RB tree Rotations
There are two type of rotations:
1-left rotation1-left rotation
2-right rotation
12

13. Left Rotations
assumption for a left rotation on a node x:
The right child of x (y) is not NIL
Idea:
rotate around the link from x to y
Makes y the new root of the sub-tree
x becomes y’s left child
y’s left child becomes x’s right child 13

14. Example: LEFT-ROTATE
14

15. Right Rotations
Assumptions for a right rotation on a node x:
The left child of y (x) is not NIL
Idea:
 Pivots around the link from y to x
 Makes x the new root of the subtree
 y becomes x’s right child
 x’s right child becomes y’s left child
15

16. Insertion
16

17. RB tree Insertion
As case in BST, first we find place where
we are to insert.
No red red child parent relation.
Red node can have only black childrenRed node can have only black children
Since inserted color is red, the black height
of the tree is remain unchanged.
 A new item is always inserted as a leaf in
the tree.
17

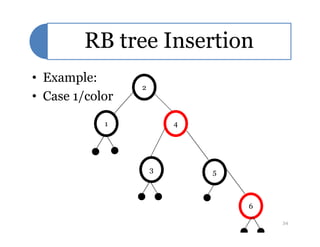
18. Case 1 – uncle y is red
C
A D
B
  
z
y
C
A D
B
  
new z
p[z]
p[p[z]]
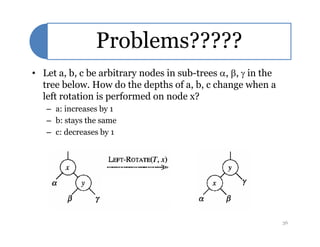
• p[p[z]] (z’s grandparent) must be black, since z and p[z] are both red
and there are no other violations of property 4.
• Make p[z] and y black  now z and p[z] are not both red. But
property 5 might now be violated.
• Make p[p[z]] red  restores property 5.
• The next iteration has p[p[z]] as the new z (i.e., z moves up 2 levels).
B
 
B
 
z is a right child here.
Similar steps if z is a left child.
18

19. Case 2 – y is black, z is a right child
C
A
B


z
y
C
B
A 

z
y
p[z]
p[z]
• Left rotate around p[z], p[z] and z switch roles  now z is
a left child, and both z and p[z] are red.
• Takes us immediately to case 3.
B

 
A
 
z
19

20. Case 3 – y is black, z is a left child
B
A
   
C
B
A 
 y
p[z]
C
z
• Make p[z] black and p[p[z]] red.
• Then right rotate on p[p[z]]. Ensures property 4 is
maintained.
• No longer have 2 reds in a row.
• p[z] is now black  no more iterations.
A
 
20

21. RB tree Insertion
• Example:
Insert 1 1
• The root can’t be red.
21

22. RB tree Insertion
• Example:
Change the color, according to 2 property.
1
22

23. RB tree Insertion
• Example:
Insert 2
1
2
23

24. RB tree Insertion
• Example:
Insert 3
1
2
3
24

25. RB tree Insertion
• Example:
Case 3
1
2
31 3
25

26. RB tree Insertion
• Example:
• Follow the property 2
1
2
31 3
26

27. RB tree Insertion
• Example:
• Insert 4
1
2
31 3
4
27

28. RB tree Insertion
• Example:
• Case 1
1
2
31 3
4
28

29. RB tree Insertion
• Example:
• Color
1
2
31 3
4
29

30. RB tree Insertion
• Example:
• Insert 5
1
2
31 3
4
5
30

31. RB tree Insertion
• Example:
• Case 3
1
2
41 4
5
3
31

32. RB tree Insertion
• Example:
• Color
1
2
41 4
53
32

33. RB tree Insertion
• Example:
• Insert 6
1
2
41 4
53
6
33

34. RB tree Insertion
• Example:
• Case 1/color
1
2
41 4
53
6
34

35. Algorithm Analysis
O(lg n) time to get through RB-Insert up to
the call of RB-Insert.
Within RB-Insert:
– Each iteration takes O(1) time.
– Each iteration but the last moves z up 2 levels.
– O(lg n) levels  O(lg n) time.
– Thus, insertion in a red-black tree takes O(lg n)
time.
35

36. Problems?????
• Let a, b, c be arbitrary nodes in sub-trees , ,  in the
tree below. How do the depths of a, b, c change when a
left rotation is performed on node x?
– a: increases by 1
– b: stays the same– b: stays the same
– c: decreases by 1
36

37. Problems?????
• What is the ratio between the longest path
and the shortest path in a red-black tree?
- The shortest path is at least bh(root)- The shortest path is at least bh(root)
- The longest path is equal to h(root)
- We know that h(root)≤2bh(root)
- Therefore, the ratio is ≤2
37