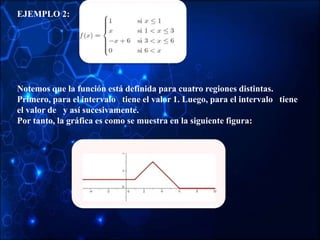
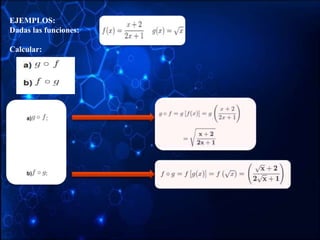
The document discusses different types of functions including:
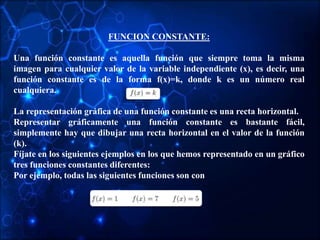
- Constant functions which always take the same output value.
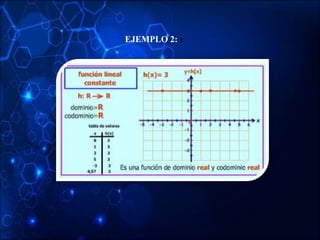
- Linear functions which are polynomials of degree 1 that pass through the origin.
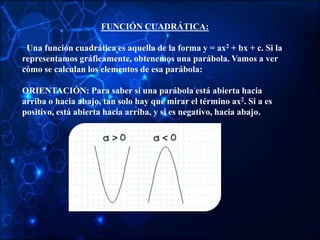
- Quadratic functions which are of the form y = ax2 + bx + c and graph as a parabola.
- Rational functions which are the quotient of two polynomials.
- Absolute value functions which output the absolute value of the input.
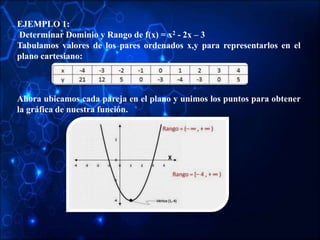
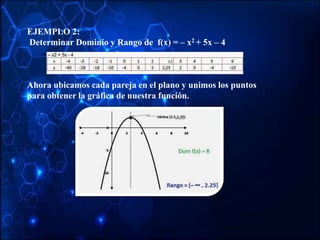
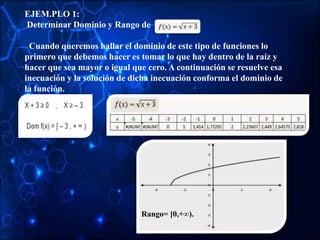
It provides examples of how to determine the domain and range of each type of function by analyzing their graphs or algebraic expressions. Key aspects like intercepts, vertex, and asymptotes are also examined.







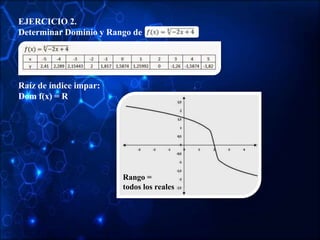



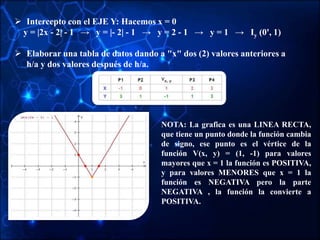
![Ahora vamos a establecer si hay valores de y para los cuales la función no
esté definida. Para ello despejamos la variable x:
La gráfica presenta una asíntota horizontal
en “Y = 2”, pero además podemos notar que
la curva que está debajo del eje “X” corta al
eje “Y” en el punto (0,-0.5). Luego el Rango
será:
Rango = (– ∞, -0.5] U (2, + ∞)
Verifique que los valores de “Y” entre “Y =
-0.5” y “Y = 2” no están señalados en la
gráfica, por lo tanto no pertenecen al
Rango.](https://image.slidesharecdn.com/funcionesjosearismendi-211205160151/85/Funciones-jose-arismendi-19-320.jpg)
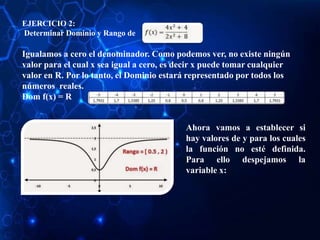


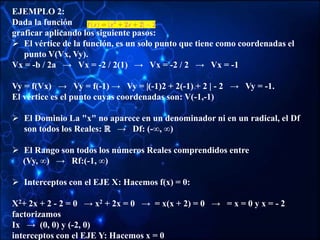
![FUNCIÓN PARTE ENTERA:
Las Funciones de Parte Entera son aquellas funciones que convierte un número
real en el número entero inmediatamente inferior.
La función parte entera se puede expresar como:
E(x) o también [x]
Veamos algunos ejemplos de funciones de parte entera:
f(x) = E(x)
Dominio todos los reales y su rango es todos los números enteros.](https://image.slidesharecdn.com/funcionesjosearismendi-211205160151/85/Funciones-jose-arismendi-27-320.jpg)
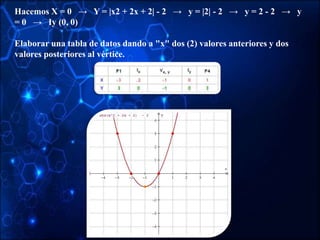
![EJEMPLO 1:
Determinar el dominio y la imagen de la función cuya gráfica es la
siguiente:
Calcular las imágenes de 1.3, 2.6,
3.1, -0.3 y -4.4.
Solución
El dominio es todos los reales.
La imagen es el conjunto de los
números naturales, NN.
Se trata de la función parte
entera: f(x)= [x] f(x)= [x].
Calculamos las imágenes:](https://image.slidesharecdn.com/funcionesjosearismendi-211205160151/85/Funciones-jose-arismendi-28-320.jpg)
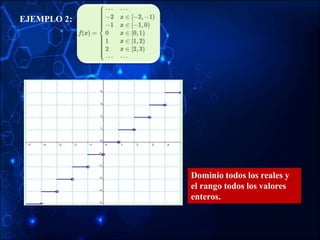

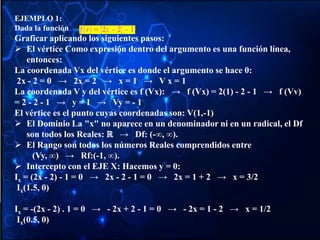
![EJEMPLO 1:
Sea la función definida así:
De acuerdo a la expresión dada notamos que la función posee tres tramos y
entre los tres cubren completamente el conjunto de los números reales. Esto
indica que su dominio es el conjunto de los números reales. Es decir;
𝐷𝑜𝑚𝑓: (−∞, +∞)
Esto se deduce de la siguiente manera:
𝑥 ≤ 0 𝑒𝑠𝑡𝑜 𝑒𝑠 ( −∞, 0] ; 0 < 𝑥 < 5 𝑒𝑠𝑡𝑜 𝑒𝑠 (0, 5) ; 𝑥 ≥ 5 𝑒𝑠𝑡𝑜 𝑒𝑠 [5 , +∞ )
Luego se unen todos estos intervalos para construir el dominio de la función:
𝐷𝑜𝑚𝑓: ( −∞, 0] ∪ (0, 5) ∪ [5, +∞) = (−∞, +∞)
La representación gráfica se puede realizar, con ayuda de tablas de valores](https://image.slidesharecdn.com/funcionesjosearismendi-211205160151/85/Funciones-jose-arismendi-31-320.jpg)