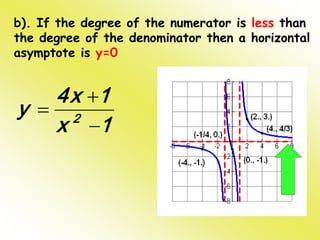
1) Rational functions are quotients of two polynomial functions. The parent rational function is f(x) = 1/x. 2) Graphs of rational functions can have vertical asymptotes where the function is undefined, horizontal asymptotes as constant lines the function approaches, and sometimes slant asymptotes. 3) Vertical asymptotes occur where the denominator is zero. Horizontal asymptotes occur depending on the relative degrees of the numerator and denominator: if the numerator degree is less than the denominator degree the horizontal asymptote is y=0, if the degrees are equal the horizontal asymptote is the quotient, and if the numerator degree is greater there is no horizontal asymptote.

1. Lesson 3.7
Graphs of Rational Functions

2. A rational function is a quotient of
two polynomial functions.
)(
)(
)(
xh
xg
xf  0)( xh
The parent function is
,
x
xf
1
)(  0x

3. I
III
a vertical asymptote x = 0
a horizontal
asymptote
y = 0

4. Example 1.
Determine the asymptotes for the graph
of f(x) = .
1
34


x
x
A vertical asymptote
Solve x +1 = 0
x = -1
Since f(-1) is undefined, there may be a
vertical asymptote at x = -1

5. A horizontal asymptote
1
34
)(



x
x
xf
1
34



x
x
y
Solve for xy(x + 1) = 4x + 3
xy + y = 4x + 3
xy - 4x = 3 - y
x(y - 4) = 3 - y
4
3



y
y
x
The rational expression is undefined
for y = 4. Thus, the horizontal
asymptote is the line y = 4.

6. The graph of this function verifies that
the lines of y = 4 and x = -1 are asymptotes.
f(x) =
1
34


x
x

7. Here’s the cheat sheet!
a) If the degree of the numerator is greater
than the degree of the denominator then
there is no a horizontal asymptote.
63x
2x
y
2




8. b). If the degree of the numerator is less than
the degree of the denominator then a horizontal
asymptote is y=0
1x
14x
y 2




9. c). If the degree of the numerator is equal to
the degree of the denominator then a horizontal
asymptote is a quotient.
16x
4x
y 2
2



4
x
4x
y 2
2



a horizontal asymptote

10. Example 2
Use the parent graph
to graph each function. Describe the transformation(s)
that take place. Identify the new location of each
asymptote.
x
1
f(x) 
a. g(x) =
To graph g(x) translate the parent
graph 2 units to the right. The new
vertical asymptote is x = 2. The
horizontal asymptote, y = 0, remains
unchanged.
2-x
1

11. b. h(x) = 3x
1

To graph h(x) , reflect the parent graph over the
x-axis, and compress the result horizontally by a
factor of 3. This does not affect the vertical
asymptote at x = 0. The horizontal asymptote,
y = 0, is also unchanged.

12. To graph m(x) , stretch the parent function
vertically by a factor of 3, and translate the
result 1 unit to the right and 2 units down. The
new vertical asymptote is x = 1. The horizontal
asymptote changes from y = 0 to
y = -2.
2
1x
3
m(x) 

c.

13. A slant asymptote occurs when the
degree of the numerator of a rational
function is exactly one degree greater
then the degree of a denominator.

14. Example 3
Determine the slant asymptote for
 
1x
42x3x
xf
2




15. a slant asymptote
a vertical asymptote
x = 1