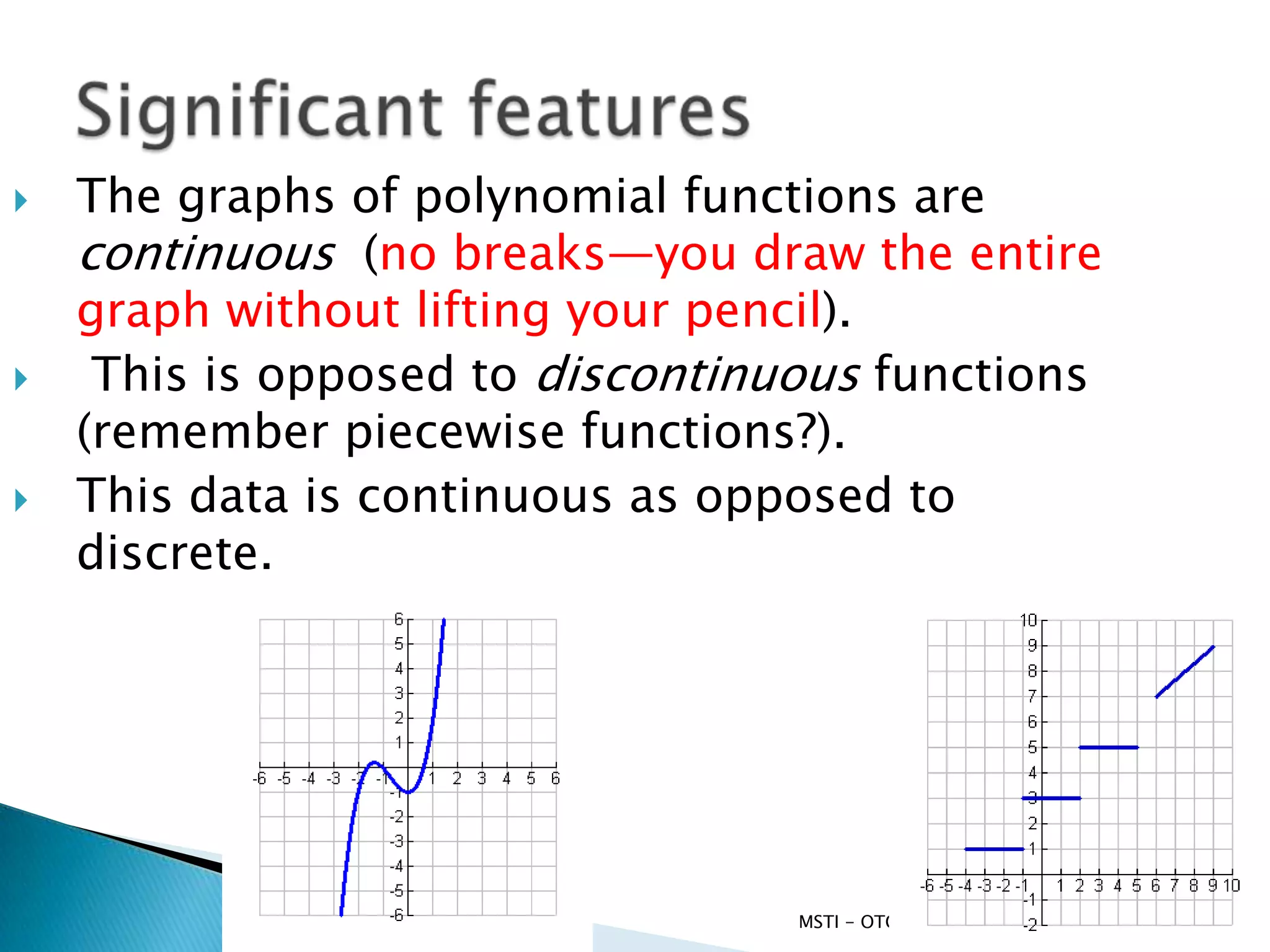
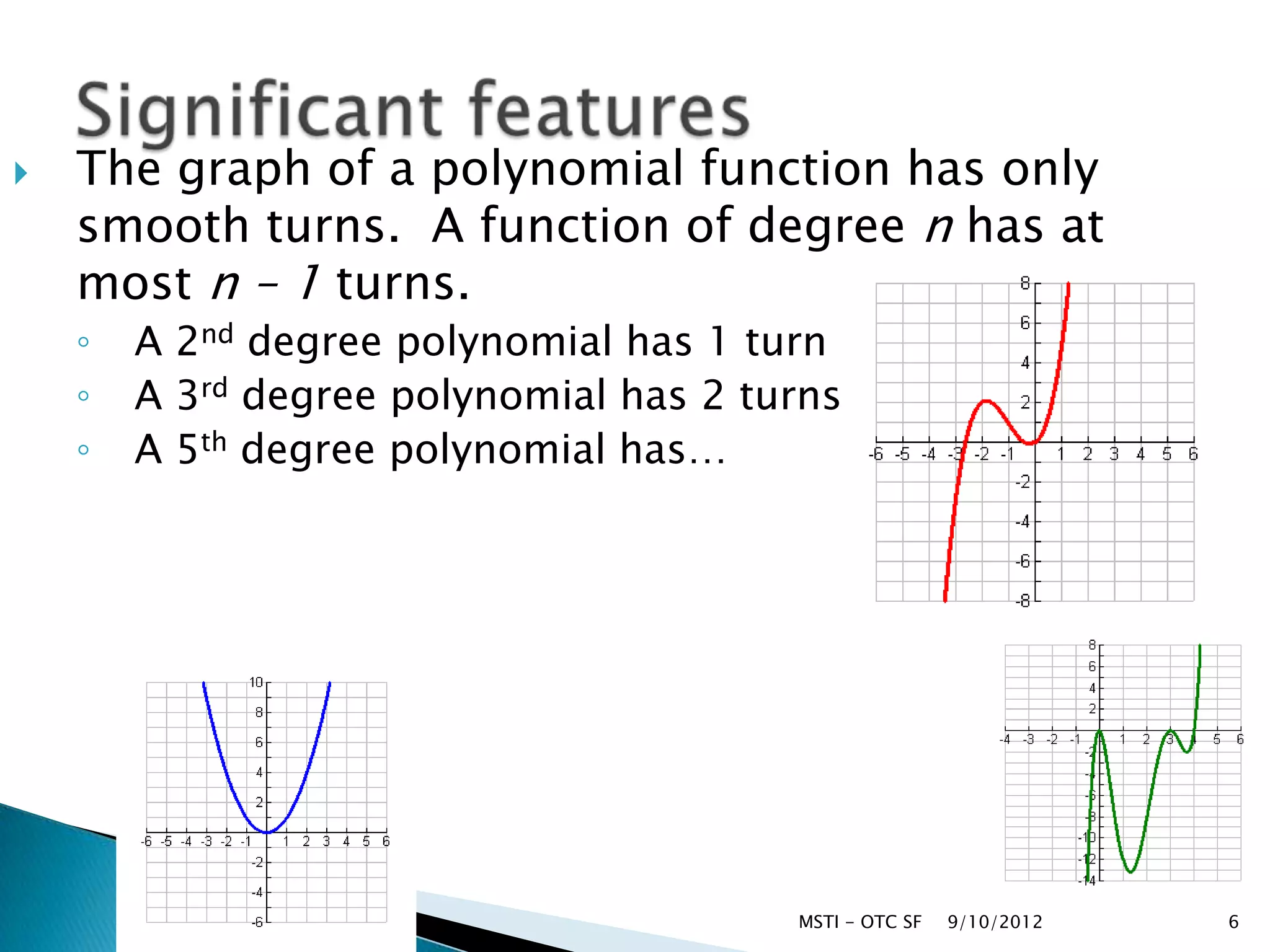
Here are the remainders when dividing the given polynomials by the specified polynomials:
1. The remainder is 0. Therefore, x-1 is a factor of x3+3x2-4x+2.
2. The remainder is 5.
3. The remainder is 0. Therefore, x+2 is a factor of 2x3+5x2+3x+11.
4. The remainder is 4.
5. The remainder is 7.
6. The remainder is 2.