Downloaded 11 times
Uploaded bySt.John's College
Microwave spectra
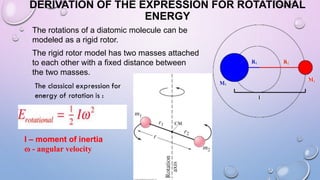
This document discusses microwave spectroscopy and its application to determining properties of gas phase molecules. It can be summarized as follows: 1) Microwave spectroscopy utilizes photons in the microwave range to cause rotational energy level transitions in gas molecules. It is applicable to molecules with a permanent dipole moment in the gas phase. 2) The rotational energy levels of diatomic molecules can be modeled using a rigid rotor approximation. This allows derivation of an expression for rotational energy levels in terms of the rotational constant B, which depends on the molecule's moment of inertia. 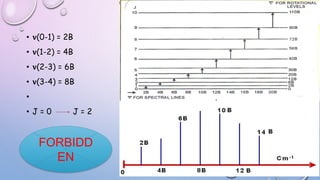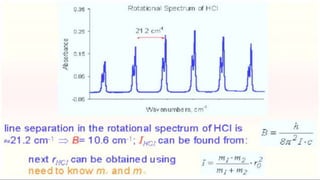3) Measurement of transition frequencies between rotational energy levels allows determination of the rotational constant B. This can then be used to calculate bond distances in diatomic molecules.
More Related Content
Microwave spectra
- 1. D. JIM LIVINGSTON FACULTYOF CHEMISTRY ST. JOHN’S COLLEGE
- 2. MICROWAVE SPECTRA • THISSPECTROSCOPY UTILIZES PHOTONS IN THE MICROWAVE RANGE TO CAUSE TRANSITIONS BETWEEN THE QUANTUM ROTATIONAL ENERGY LEVELS OF A GAS MOLECULE. • MICROWAVE REGION – 10-3 to 10-1m •Why Gas Phase? • INTERMOLECULAR INTERACTIONS HINDERING ROTATIONS IN THE LIQUID AND SOLID PHASES OF THE MOLECULE. •Condition • Molecule must posses a permanent dipole moment.
- 3. DIPOLE MOMENT • ADIPOLE MOMENT IS A QUANTITY THAT DESCRIBES TWO OPPOSITE CHARGES SEPARATED BY A DISTANCE • BY DEFINITION THE DIPOLE MOMENT, Μ, IS THE PRODUCT OF THE MAGNITUDE OF THE SEPARATED CHARGE AND THE DISTANCE OF THE SEPARATION When atoms in a molecule share electrons unequally, they create what is called a dipole moment.
- 4. WHICH MOLECULES EXHIBITMICROWAVE SPECTRA? • HOMONUCLEAR DIATOMIC MOLECULES: MICROWAVE INACTIVE • H2,O2, Cl2, CO2,C6H6 – ZERO DIPOLE MOMENT ( NO CHARGE SEPARATION) • HETERONUCLEAR DIATOMIC MOLECULES: MICROWAVE ACTIVE • HCl, HBr, CO, NO – PERMANENT DIPOLE MOMENT (CHARGE SEPARATION) • SELECTION RULE: • A SELECTION RULE, OR TRANSITION RULE, FORMALLY CONSTRAINS THE POSSIBLE TRANSITIONS OF A SYSTEM FROM ONE QUANTUM STATE TO ANOTHER. • SELECTION RULES HAVE BEEN DERIVED FOR ELECTROMAGNETIC TRANSITIONS IN MOLECULES, IN ATOMS, IN ATOMIC NUCLEI, AND SO ON. • FOR ROTATIONAL SPECTRA ΔJ = ±1.
- 5. DERIVATION OF THEEXPRESSION FOR ROTATIONAL ENERGY The rotations of a diatomic molecule can be modeled as a rigid rotor. The rigid rotor model has two masses attached to each other with a fixed distance between the two masses. I – moment of inertia ɷ - angular velocity
- 6. Assume a rigid(not elastic) bond r0 = r1 + r2 Center of gravity, C : m1r1 = m2r2 m1r1 = m2 (r0 - r1) = m2r0 - m2r1 m2r0 = m1r1 + m2r1 m2r0 = (m1 + m2) r1 21 01 2 mm rm r
- 7. • THE MOMENTOF INERTIA • I = Σ miri 2 ( ri - distance ith of particle of mass mi from cg) • For diatomic particle , I = m1r1 2 + m2r2 2 • Substituting the values of r1 and r2, • 𝑰 = 𝒎 𝟏 𝒎 𝟐 𝟐 𝒎 𝟏 +𝒎 𝟐 𝟐 𝒓 𝟐 + 𝒎 𝟏 𝟐 𝒎 𝟐 𝒎 𝟏 +𝒎 𝟐 𝟐 𝒓 𝟐 • I= 𝒎 𝟏 𝒎 𝟐 𝒎 𝟏 +𝒎 𝟐 𝒓 𝟐 • µ - reduced mass. I = µr2
- 8. • ANGULAR MOMENTUML = IW (W – ANGULAR VELOCITY) • THE QUANTIZED ANGULAR VELOCITY IS GIVEN BY • L = 𝐽 𝐽 + 1 h/2Π ( J= 0,1,2,3… ROTATIONAL Q. NO) • ENERGY OF ROTATION • Multiply and divide by I, • E = (IW)2/2I • E = L2 / 2I • Sub. Value of L, • E = ℎ 2 8π 2 𝐼 𝐽 (𝐽+1)
- 9. • To expressenergy in cm-1, • F(J) = E/ hc = ℎ 8π2 𝐼𝑐 𝐽 (𝐽+1) cm-1 • F(J) – total rotational energy (rotational term) • B – rotational constant F(J) = BJ (J+1) B = h/8π2Ic
- 10. SELECTION RULE • Transitionsin which rot. Q.No increase or decrease by unity are allowed. Transition from J to J+1, Energy difference 𝚫E = EJ+1 – EJ 𝛎J J+1 = B(J+1)(J+2) – BJ(J+1) = B(J2+3J+2) – B(J2+J) = 2B(J+1)cm-1 J = 𝚫 ± 1 F(J) = BJ (J+1)
- 11. • 𝛎(0-1) =2B • 𝛎(1-2) = 4B • 𝛎(2-3) = 6B • 𝛎(3-4) = 8B • • J = 0 J = 2 FORBIDD EN
- 13. DETERMINATION OF BONDDISTANCE