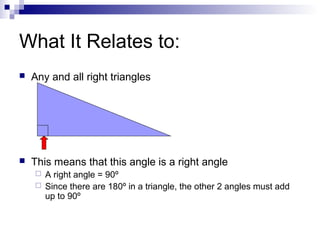
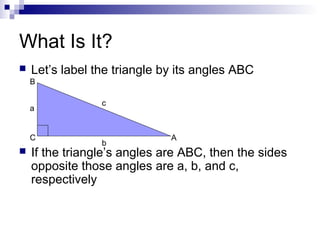
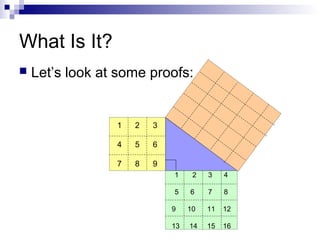
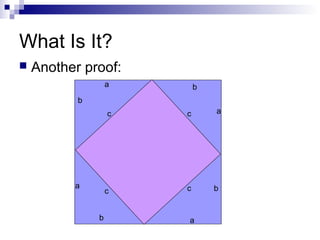
Pythagoras was an ancient Greek thinker, but he was not the founder of the Pythagorean theorem. That honor goes to his followers, known as the Pythagorean Brotherhood, who established the theorem over 100 years after Pythagoras' death. The Pythagorean theorem states that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. This relationship has many practical applications in fields like engineering, construction, physics, and astronomy that involve calculating distances.

1. The Pythagorean
Theorem
By Kaamil Ali

2. Who was Pythagoras?
 An ancient Greek thinker who was fond of poetry
and literature
 He himself was not a geometer
 His followers, dubbed the Pythagorean
Brotherhood, were a religious cult
 Contrary to popular belief, Pythagoras was NOT
the founder of the Pythagorean Theorem
 The Pythagorean Brotherhood founded the theorem
over 100 years after Pythagoras had died

3. What It Relates to:
 Any and all right triangles
 This means that this angle is a right angle
 A right angle = 90º
 Since there are 180º in a triangle, the other 2 angles must add
up to 90º

4. What Is It?
 Let’s label the triangle by its angles ABC
 If the triangle’s angles are ABC, then the sides
opposite those angles are a, b, and c,
respectively
AC
B
b
a
c

5. What Is It?
 a and b are the sides, or legs, of the right
triangle
 c is the hypotenuse, or the side opposite the
right angle, which is always the longest side of
the right triangle
 In any triangle, the sums of any 2 sides is
greater than the length of the 3rd
side, so:
 a + b > c
 a + c > b
 b + c > a

6. What Is It?
 However, sometimes when we square the sides,
the sum of the squares is equal to the square of
the hypotenuse
 a2
+ b2
= c2
 This is the Pythagorean Theorem
 The Pythagorean Theorem states:
 In any right triangle, the sum of the squares of the 2 sides is
equal to the square of the hypotenuse.
 Conversely, if the sum of the squares of the 2 sides is equal
to the square of the hypotenuse, then you have a right
triangle.

7. What Is It?
 What does this mean?
It means that, if you have a right triangle, you
know that the squares of the 2 sides will
always add up to the square of the
hypotenuse.
It means that if you have a triangle in which
the squares of the 2 sides add up to the
square of the hypotenuse, you know you have
a right triangle.

8. What Is It?
 Let’s look at some proofs:
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
1 2 3
4 5 6
7 8 9

9. What Is It?
 If you add up all of the little squares, i.e. 9
+ 16, you get 25. This is in accord with 32
+ 42
= 52
 Here, we see that the lengths of the sides
are 3 and 4, and the length of the
hypotenuse is 5.
 Using the Pythagorean Theorem, we get
32
+ 42
= 52
, or 9 + 16 = 25.

10. What Is It?
 Another proof:
cc
c c
b
b
b
b
a
a
a
a

11. What Is It?
 What is the area of the large blue square?
 By multiplying the length by the width, we get (a + b)2
 Simplify to a2
+ 2ab + b2
 By adding up the areas of 4 small blue triangles and
the 1 small purple square, we get, 4(1/2)ab + c2
 Simplify to 2ab + c2
 If we set the areas equal to each other, we get a2
+
2ab + b2
= 2ab + c2
 The 2ab’s cancel out, so we get a2
+ b2
= c2
 Thus, the Pythagorean Theorem has been once
again proven.

12. What Is It?
 The Pythagorean Theorem specifically refers to
squares of the sides, however any 2-
dimensional relation between the 2 sides and
the hypotenuse would work
 If we drew circles on each side and the hypotenuse,
with the sides as the diameter of each respective
circle, then the areas of the circles on the 2 sides will
sum up to the area of the circle on the hypotenuse
 Algebraically, this is seen as ka2
+ kb2
= kc2
since k
can be factored out, where k is some constant

13. Practice
 Find the missing lengths:
 a = 3, b = 4, c = ?
 a = 7, b = ?, c = 25
 a = ?, b = 12, c = 13
 Are triangles with the following lengths right
triangles?
 a = 7, b = 8, c = 9
 a = 12, b = 16, c = 20
 a = 11, b = 58, c = 61

14. Practice
 To get from point A to point B you must avoid
walking through a pond. To avoid the pond, you
must walk 34 meters south and 41 meters east.
To the nearest meter, how many meters would
be saved if it were possible to walk through the
pond?
 A baseball diamond is a square with sides of 90
feet. What is the shortest distance, to
thenearest tenth of a foot, between first base
and third base?

15. Practice
 In a computer catalog, a computer monitor is
listed as being 19 inches. This distance is the
diagonal distance across the screen. If the
screen measures 10 inches in height, what is the
actual width of the screen to the nearest inch?
 Oscar's dog house is shaped like a tent. The
slanted sides are both 5 feet long and the
bottom of the house is 6 feet across. What is
the height of his dog house, in feet, at its tallest
point?

16. Why Does It Matter?
 The Pythagorean Theorem allows us to do many
things in real-life situations.
 The professional fields in which it is useful are:
 Civil Engineering
 Construction
 Astronomy
 Physics
 Particle Physics
 Advanced Mathematics
 Ancient Warfare

17. Why Does It Matter?
 Civil Engineering:
Building bridges
Measuring distances across rivers in order to
determine the lengths of proposed bridges
Building foundations of skyscrapers
 Construction
Measuring angles
Ensuring solid and level foundations

18. Why Does It Matter?
 Astronomy
Measuring distances in a 3-dimensional
space
Calculating shadows cast by astronomical
bodies
 Physics
Determining pressure in bridge construction
Understanding ramps, levers, and screws

19. Why Does It Matter?
 Particle Physics
 Calculating distances of particles in 3-dimensional space
 Advanced Mathematics
 Pythagorean Triples
 Trigonometry and the Unit Circle
 Vectors
 Calculating distances between points on a Cartesian Plane
 Ancient Warfare
 The Ancient Romans used it to measure the distance that
catapults had to be from their target

20. Food for Thought
 The distance formula for 2 points on a Cartesian Plane is derived
from the Pythagorean Theorem
 The distance formula is d = √[(x2 – x1)2
+ (y2 – y1)2
]
 This is simply a variation on c = √(a2
+ b2
), which is the Pythagorean
Theorem if you solve for c2
 Pythagorean Triples are sets of 3 numbers that fit the criteria of a2
+
b2
= c2
 Since any set of Pythagorean Triples can be multiplied by an infinite
amount of constants, there are an infinite amount of Pythagorean
Triples
 If triangles with side lengths that corresponded to every Primitive
Pythagorean Triple (reduced by greatest common factor) were drawn on
a Cartesian Plane, we would end up with a unit circle, which is where
our Trigonometric functions come from