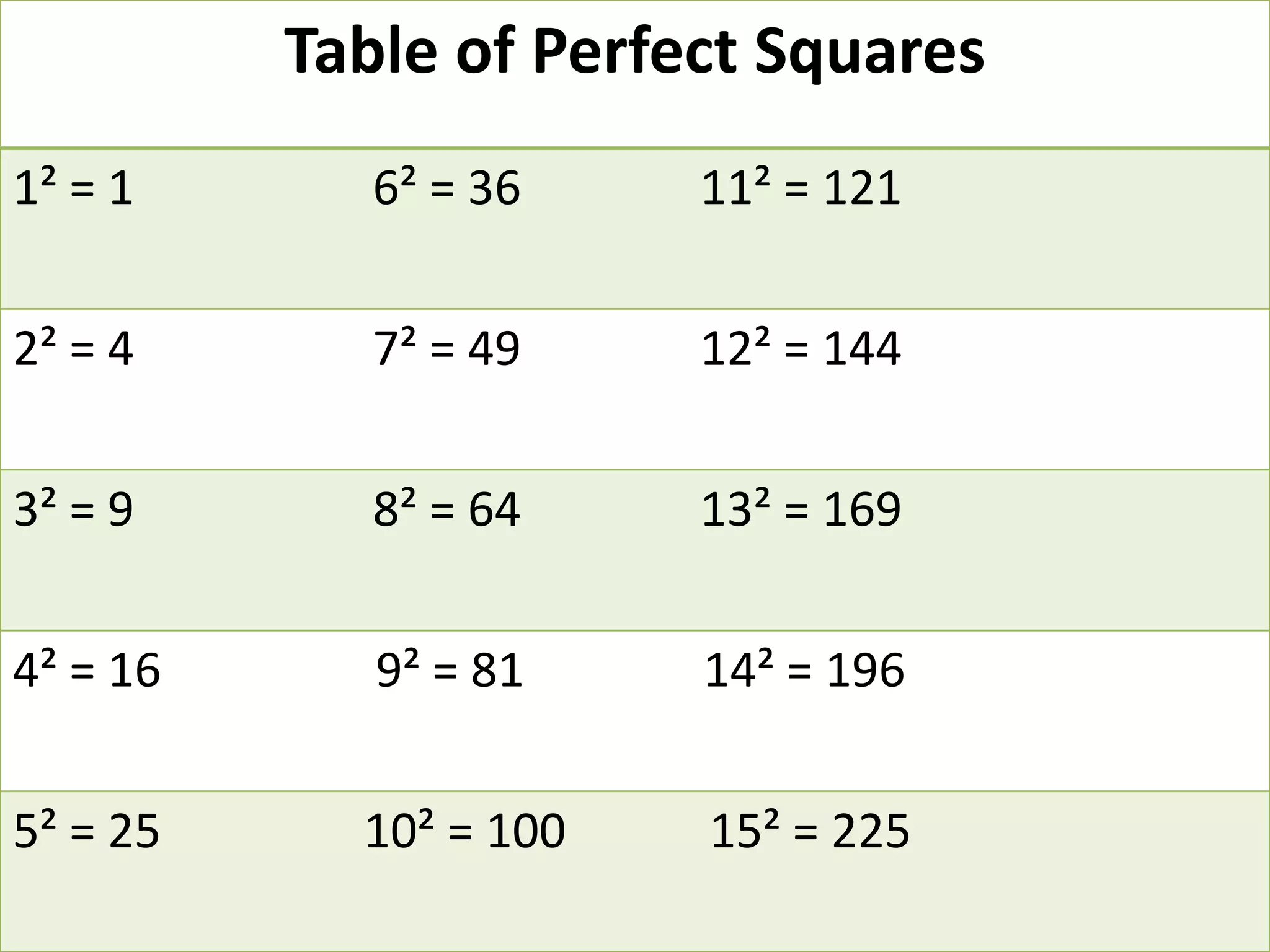
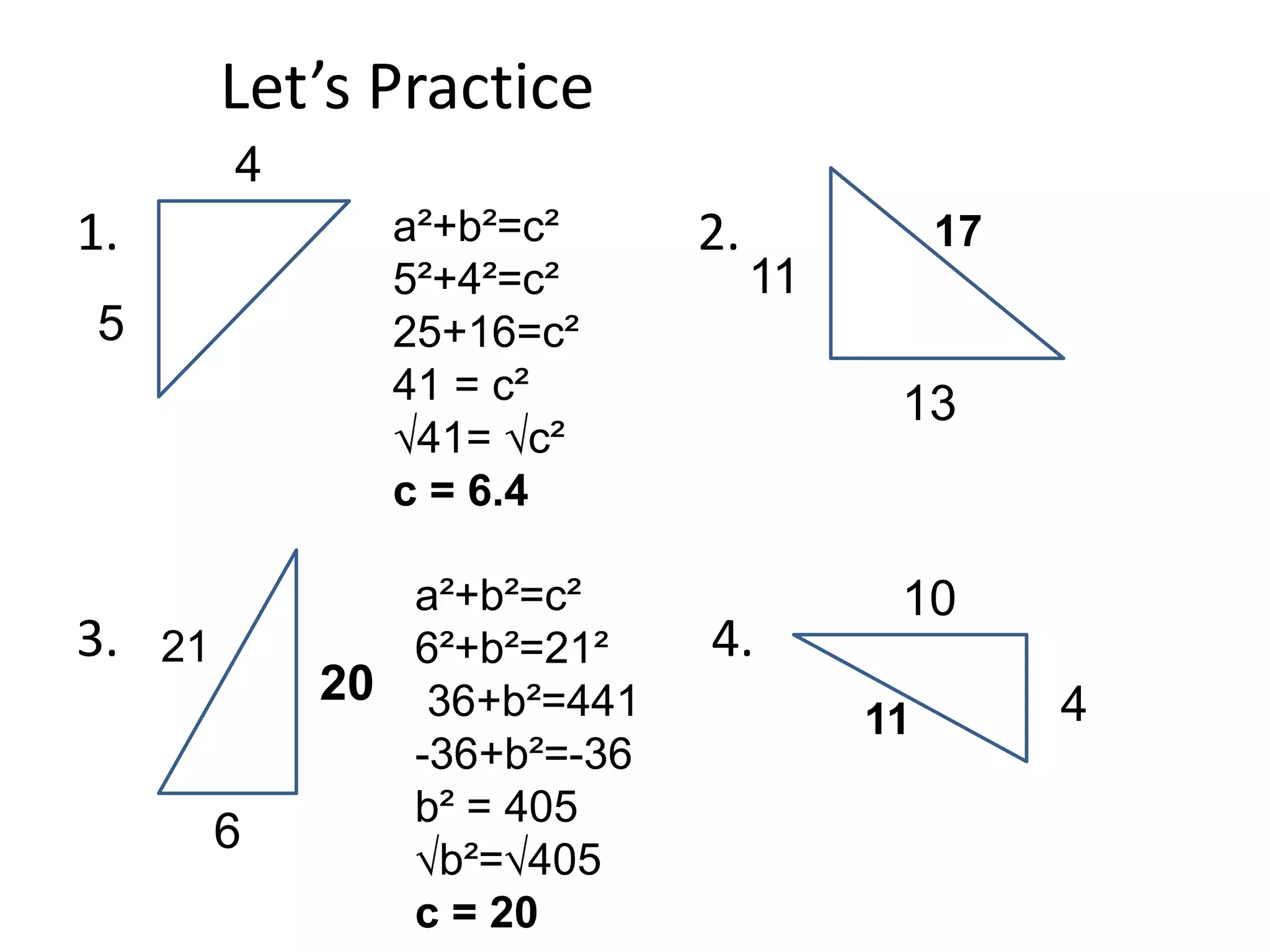
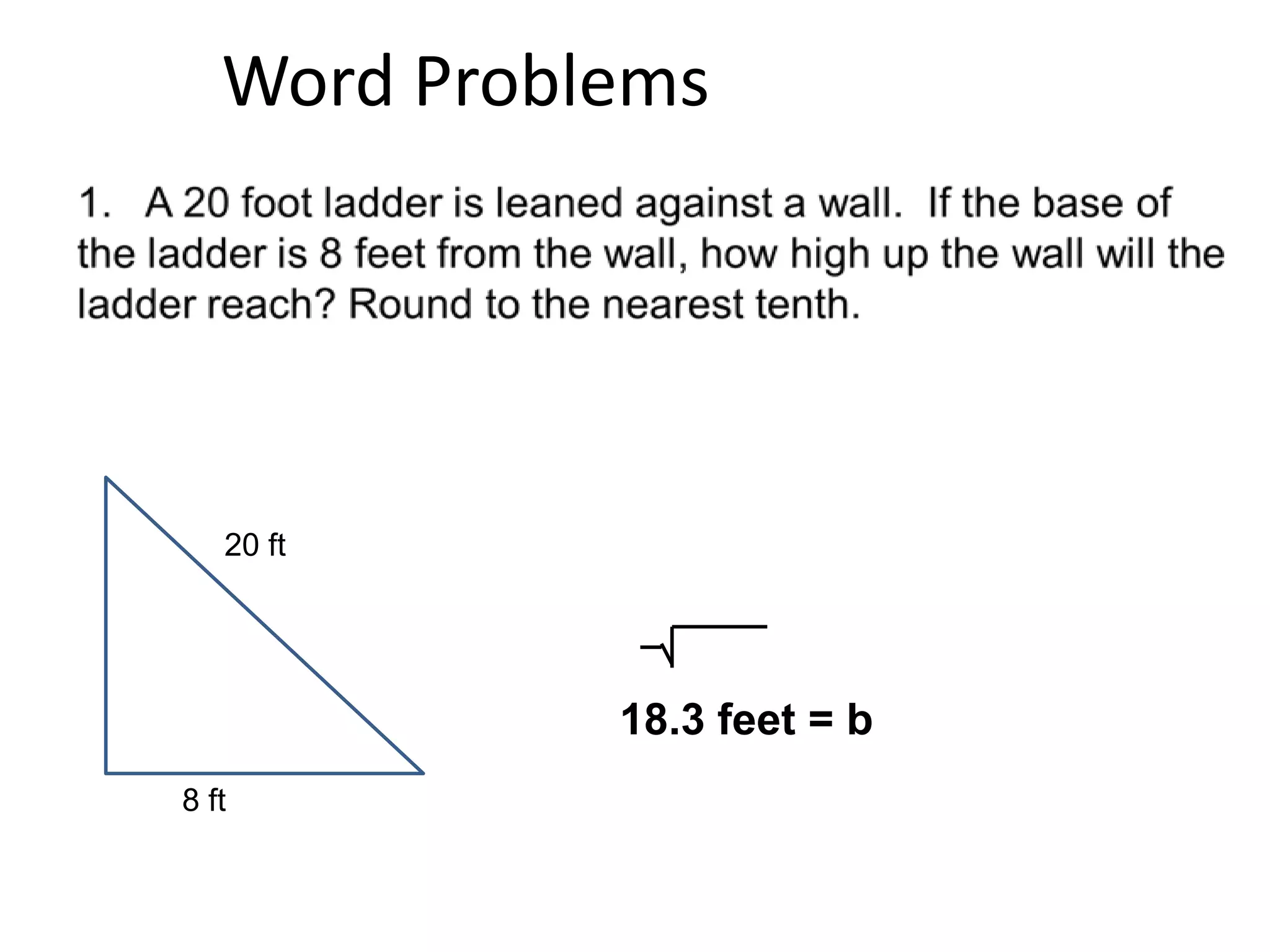
The document provides instruction on the Pythagorean theorem. It defines squares and square roots, provides examples of perfect squares, and explains how to find the square root of a number. It then introduces the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. The document provides examples of when the theorem can be used and how to set up and solve Pythagorean theorem problems and word problems. Finally, it provides examples of solving word problems using the Pythagorean theorem.

1. Pythagorean Theorem
Lesson 5
Tennessee
Adult Education
This curriculum was written with funding of the Tennessee Department of Labor and Workforce Development and may not be reproduced in any way without written permission. ©

2. Squares
•Before solving Pythagorean Theorem
problems, a student must understand the
concept of squares and square roots.
•The square of a number is that number
multiplied by itself. For example, the square of 5
is 5 x 5 =25.
•In symbols, you write the square of a number
as a base and an exponent.
5² exponent
5 x 5 is written 5²
base

3. Table of Perfect Squares
1² = 1 6² = 36 11² = 121
2² = 4 7² = 49 12² = 144
3² = 9 8² = 64 13² = 169
4² = 16 9² = 81 14² = 196
5² = 25 10² = 100 15² = 225

4. Square root - The square root of a number is a number
that is multiplied by itself to get a number. √ is the
symbol for finding the square root.
Example: √25 = 5 ; in other words 5 x 5 = 25
√36 = 6 ; in other words 6 x 6 = 36
The square root of a number is found by asking, “What
number times itself equals this?”
For example: What number times itself equals 4?

5. Guided Practice
Directions: What is the value of each
squared number or letter below?
1. 3² = ____
9 2. 8² = ____
64 3. 12² = ____
144
4. 10² = ____
100 5. a² if a = 4 _____
16
6. x² if x = 13 _____ 7. b² if b = 18 _____
169 324

6. Pythagorean Theorem
•Is used to find the third side of a right triangle when the
other two sides are known.
•Key Terms: c
•a & b are known as the legs. a
• c is known as the hypotenuse.
b
•The hypotenuse will always be the opposite side of the
right angle.
•The formula for solving Pythagorean problems is:
a² + b² = c²

7. Pythagorean Theorem
•All word problems that create a right triangle are
considered a Pythagorean problem. You will have to
recognize the triangle. The test will NOT tell you that
it is a Pythagorean problem. Here are some
examples of when to use the formula a² + b² = c²:
• Building a ramp
• Crossing a field
• Pouring a sidewalk
• Installing a temporary pole, etc.
• Leaning a ladder up against a wall/tree.

8. Pythagorean Theorem
•When you are solving pythagorean word
problems you will need to identify what sides you
are looking for. The following words be used to
refer to the hypotenuse, side c:
• diagonal
• direct distance
• directly
• any intermediary directions (NW,NE,SW,SE)

9. Let’s Practice
4
1. a²+b²=c² 2. 17
5²+4²=c² 11
5 25+16=c²
41 = c² 13
41= c²
c = 6.4
a²+b²=c² 10
3. 21 6²+b²=21² 4.
20 36+b²=441 4
11
-36+b²=-36
b² = 405
6
b²= 405
c = 20

10. Word Problems
20 ft
18.3 feet = b
8 ft

11. 2. George rides a bike 9 km south and then 12 km east. How far
is he from his starting point?
9 km
15 km
12 km

12. 3. Find the length of a rectangle that has a diagonal of 25 feet
and a width of 15 feet.
c² - a² = b²
25 ft
15 ft 25² - 15² = b²
625 – 225 = b²
400 = b²
20 = b