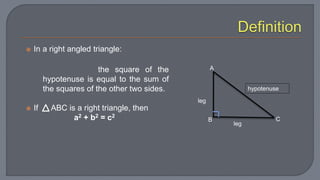
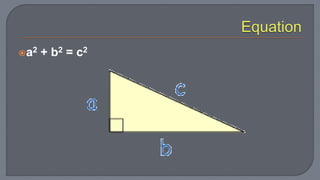
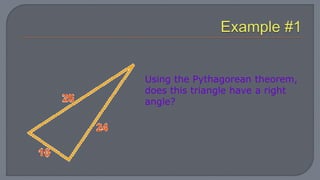
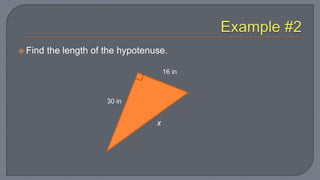
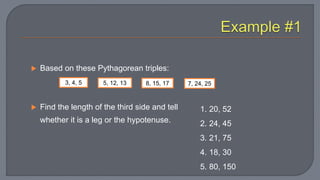
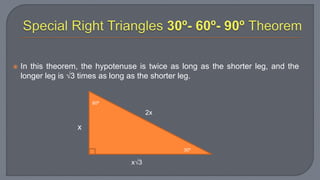
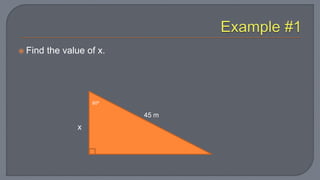
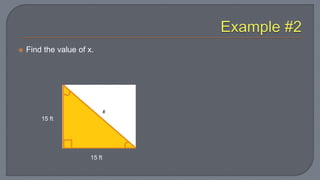
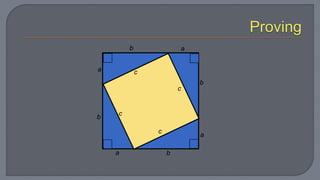
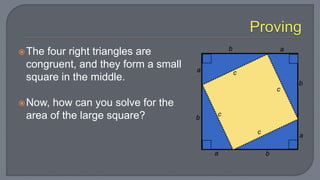
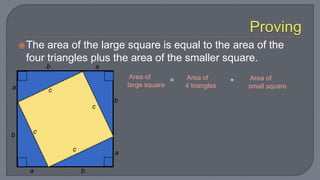
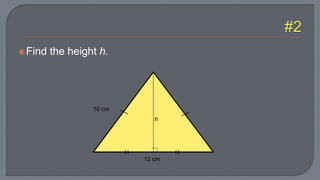
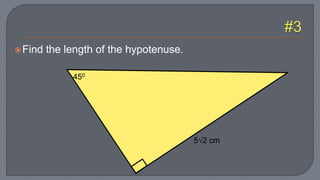
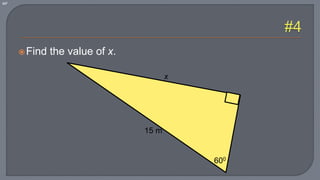
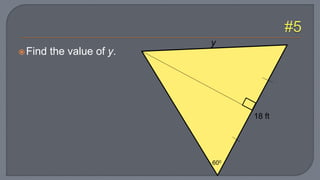
The document discusses the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. It provides examples of using the theorem to determine whether a triangle is right, acute, or obtuse based on the side lengths. It also discusses classifying triangles, finding missing side lengths, and explores Pythagorean triples.

1. Gallego
Garridos
Lopoz
Radjac
Tejano

3.  In a right angled triangle:
the square of the
hypotenuse is equal to the sum of
the squares of the other two sides.
 If ABC is a right triangle, then
a2 + b2 = c2
hypotenuse
leg
leg
A
CB

4.  If we know the lengths of two sides of a right angled triangle, we can find the
length of the third side.
 (But remember it only works on right angled triangles!)

5. a2 + b2 = c2

6. Using the Pythagorean theorem,
does this triangle have a right
angle?

7.  a2 + b2 = c2 ?
 c2 = a2 + b2
 c2 = 102 + 242
 c2 = 100 + 576
 c2 = 676
 c2 = 262 = 676
 They are equal, so ...
 Yes, it does have a right angle!

8.  Find the length of the hypotenuse.
16 in
30 in
x

9.  Pythagorean Theorem; a2 + b2 = x2 ?
 x2 = a2 + b2
 x2 = 302 in + 162 in
 x2 = 900 in2 + 256 in2
 x2 =1156 in2
 x=34 in
16 in
30 in
x

10. A Pythagorean triple is a set of three positive
integers a, b, and c that satisfy the equation a2 +
b2 = c2 .
Common Pythagorean Triples and Some of their Multiples
3, 4, 5 5, 12, 13 8, 15, 17 7, 24, 25
6, 8, 10 10, 24, 26 16, 30, 34 14, 48, 50
30, 40, 50 50, 120, 130 80, 150, 170 70, 240, 250
3x, 4x, 5x 5x, 12x, 13x 8x, 15x, 17x 7x, 24x, 25x
The most common Pythagorean triples are in bold. The other triples are the result
of multiplying each integer in a bold face triple by the same factor.

11.  Based on these Pythagorean triples:
 Find the length of the third side and tell
whether it is a leg or the hypotenuse.
3, 4, 5 5, 12, 13 8, 15, 17 7, 24, 25
1. 20, 52
2. 24, 45
3. 21, 75
4. 18, 30
5. 80, 150

12. 1. 20, 48
2. 24, 45 4. 18, 30
3. 21, 75 5. 80, 150
A common Pythagorean triple is 5,12,13. Notice that if you multiply the lengths of the
legs of the Pythagorean triple by 4, you get the lengths of the legs of the triangle:
5(4) = 20 and 12(4) = 48 and the hypotenuse is 13(4) = 52.
To complete the Pythagorean triple, the third side is 52 and is the hypotenuse.
(The same method for the rest)
Third side : 51
Hypotenuse
Third side : 72
Leg
Third side : 170
Hypotenuse
Third side : 24
Leg

13.  The "special" nature of these triangles is their
ability to yield exact answers instead of decimal
approximations when dealing with trigonometric
functions.

14.  In this theorem, the hypotenuse is twice as long as the shorter leg, and the
longer leg is 3 times as long as the shorter leg.
60º
30º
2x
x3
x

15.  In this theorem , the hypotenuse is 2 times as long as each leg.
45º
45º
x2
x
x

16.  Find the value of x.
60º
45 m
x

17.  Find the value of x.
15 ft
15 ft
xx

18. There are many proofs of the Pythagorean Theorem. An informal/direct proof will be shown.

19. c
c
c
a
a
a
a
b
b
b
b

20. The four right triangles are
congruent, and they form a small
square in the middle.
Now, how can you solve for the
area of the large square?
c
c
c
a
a
a
a
b
b
b
b

21. The area of the large square is equal to the area of the
four triangles plus the area of the smaller square.
c
c
c
a
a
a
a
b
b
b
b
Area of
large square
= +Area of
4 triangles
Area of
small square

22. (a + b) 2 = 4(1/2) (ab) + c2
(a + b) 2 = 4(ab/2) + c2
(a + b) 2 = 2ab + c2
a2 + 2ab + b2 = 2ab + c2
a2 + b2 = c2
c2 = a2 + b2
Area of
large square
= +Area of
4 triangles
Area of
small square
 by area formulas
Division
Multiplication
Subtract 2ab on both sides
Reflexive Property

23. How can you classify a triangle according to its side length when using pythagorean
theorem and its given lengths?

24. If the square of the length of the longest side of a triangle
is equal to the sum of the squares of the lengts of the
other two sides, then the triangle is a right triangle.
If a2 + b2 = c2 , then
ABC is right triangle.
longestside 2
side1
A
CB

25. If the square of the length of the longest side of a triangle
is less than the sum of the squares of the lengths of the
other two sides, then the triangle is an ACUTE
TRIANGLE.
If c2 < a2 + b2 , then
ABC is obtuse triangle.
A
C
B

26. If the square of the length of the longest side of a triangle
is greater than the sum of the squares of the lengths of
the other two sides, then the triangle is an OBTUSE
TRIANGLE.
If c2 > a2 + b2 , then
ABC is obtuse triangle.
A
CB

27. Classify if its acute, obtuse, or right triangle with the given
side length measurements.
1. 1, 12, 1
2. 6,9,10
3. 3,7,4
4. 13,6,12
5. 2,4,5
Right
Acute
Obtuse
Acute
Obtuse

28. https://www.mathsisfun.com/pythagoras.html
http://www.regentsprep.org/regents/math/algtrig/att2/ltri30.
htm
http://www.regentsprep.org/regents/math/algtrig/att2/ltri45.
htm

29. Answer on a ½ crosswise sheet of paper

30. Derive the value of x using the given measurements and
Pythagorean Theorem.
x
3f
2d

31. Find the height h.
10 cm
12 cm
h

32. Find the length of the hypotenuse.
450
52 cm

33. Find the value of x.
600600600
600
15 m
x

34. Find the value of y.
600
18 ft
y