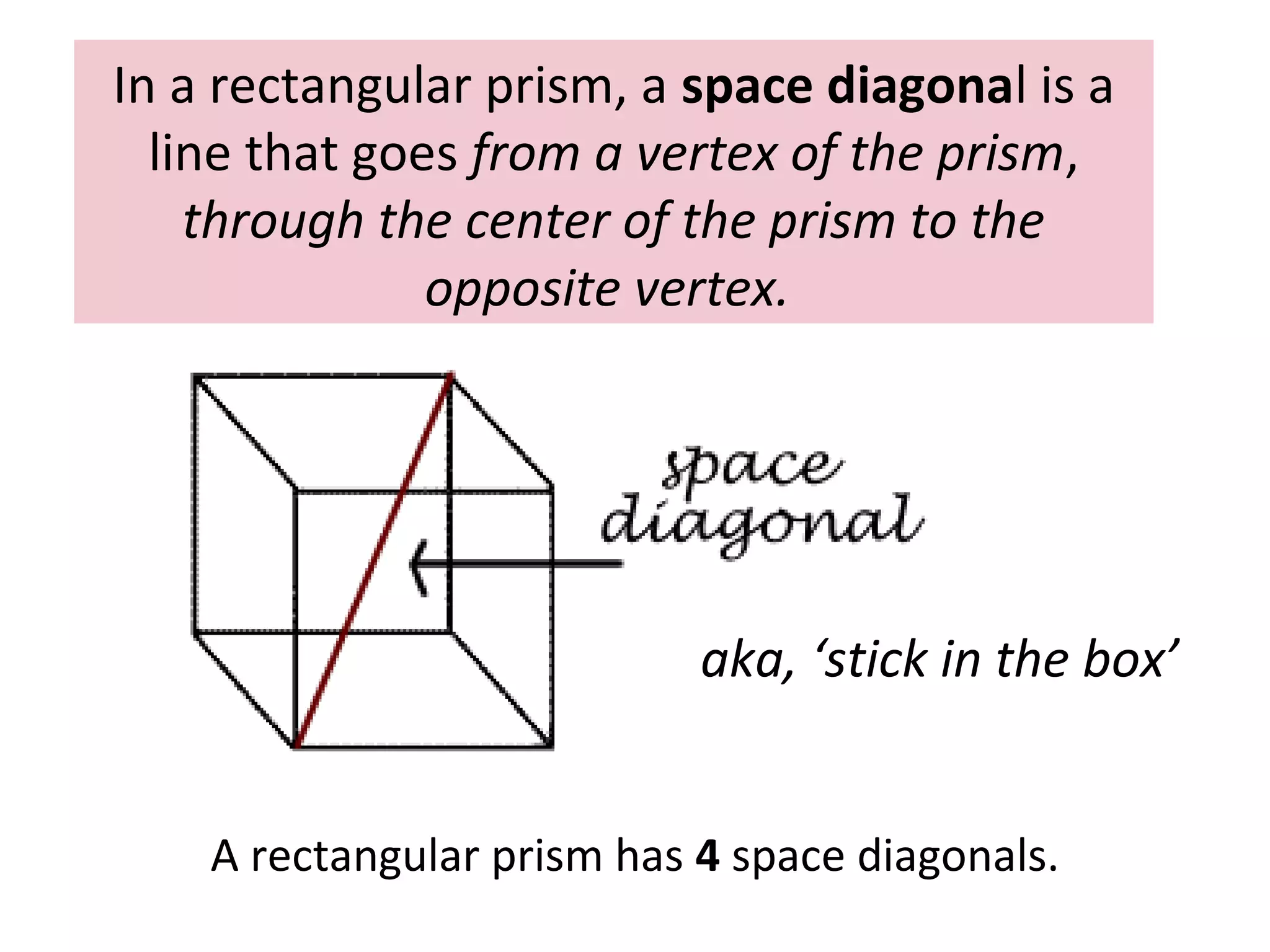
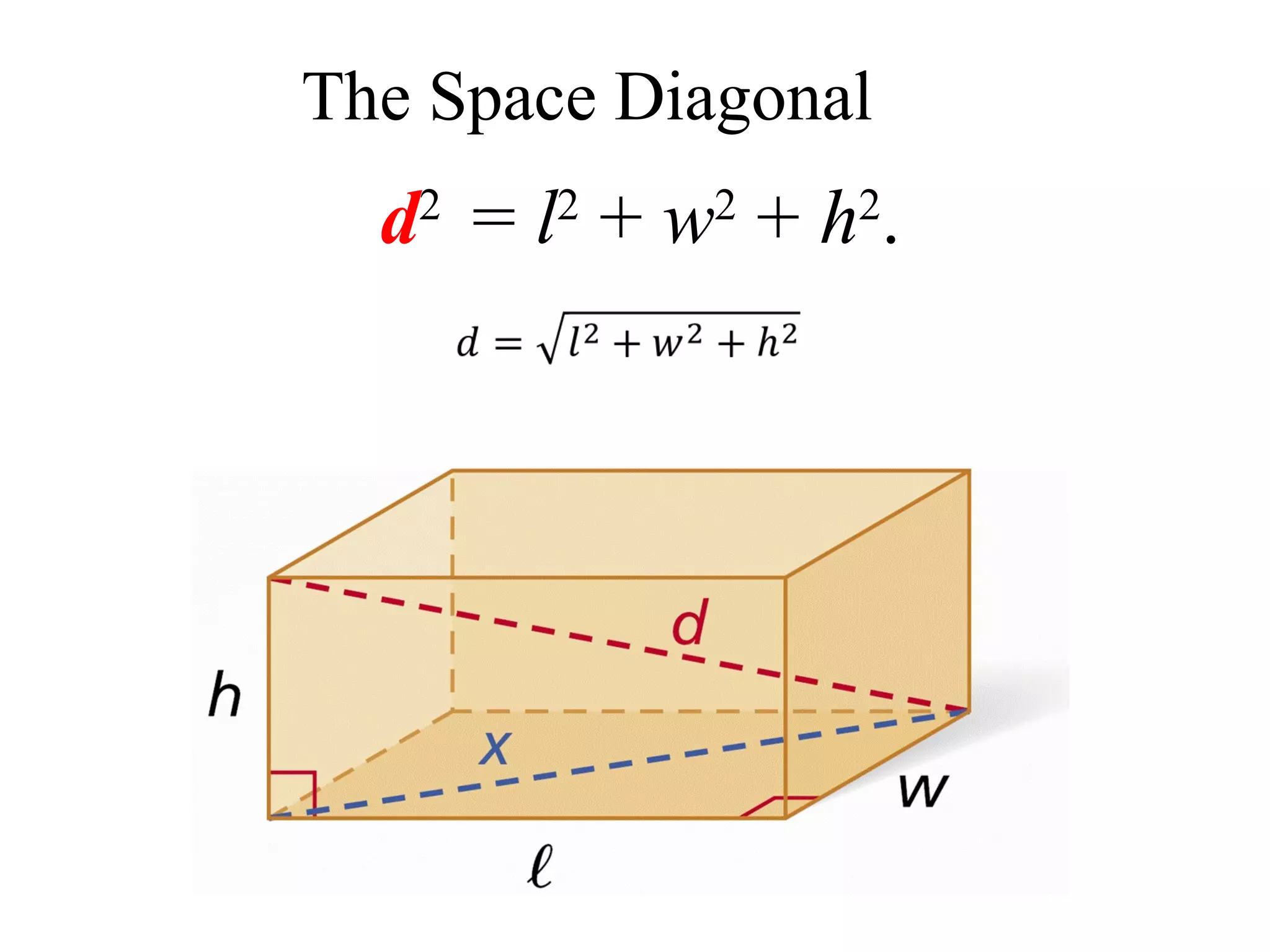
(1) A space diagonal is a line that connects opposite vertices through the center of a rectangular prism. (2) The Pythagorean theorem can be used to calculate the length of a space diagonal by treating it as the hypotenuse of a right triangle formed by the dimensions of the prism. (3) For example, in a prism measuring 28cm by 12cm by 16cm, the space diagonal AG is calculated to be 34.4cm using the Pythagorean theorem and considering triangles ABC and ACG.

1. Space Diagonal
The Pythagorean Theorem in 3D

2. In a rectangular prism, a space diagonal is a
line that goes from a vertex of the prism,
through the center of the prism to the
opposite vertex.
A rectangular prism has 4 space diagonals.
aka, ‘stick in the box’

3. The Pythagorean Theorem is useful when
we need to find the length of a space
diagonal in a rectangular prism.
Side c is the space diagonal.
Space Diagonal

4. F
28cm
12cm
16cm
A B
C
D
E
GH
Finding The Length Of A Space Diagonal.
Look at the rectangular prism below:
It is our task to calculate the length of the space diagonal AG
which runs through the space inside the rectangular prism.
(1) Start by considering
the triangle ABC.
(2) Calculate the length
of AC.
AC ≈ 30.5cm
A
C
28
12
B22
1228 +=AC

5. Now look at the box again.
F
28cm
12cm
16cm
A B
C
D
E
GH
30.5cm
(3) Now consider triangle
ACG.
(4) Calculate the length of
AG.
A
G
30.5
16
AG =
AG = 34.4cm
( ) ( )22
165.30 +
C

6. OR
OR
OR
OR
OR
OR
OROR
OR

7. A diagonal of a three-dimensional figure connects
two vertices of two different faces.
Diagonal d of a rectangular prism is shown in the diagram.
Using substitution, d2
=l2
+ w2
+ h2
.
By the Pythagorean Theorem,
l2
+ w2
= x2
and x2
+ h2
= d2
.

8. Pythagorean Theorem
2D vs 3D
c
b
d
22
cbd +=
222
cbah ++=

9. d2
= l2
+ w2
+ h2
.
The Space Diagonal

10. Space Diagonal
Pythagoras In 3D Shapes.
F
28cm
12cm
16cm
A B
C
D
E
GH
222
161228 ++=AG
41.341184 ≈=AG
222
CGBCABAG ++=

11. What Goes In The Box ?
Calculate the lengths of the space diagonals in
the rectangular prisms below:
(1)
4m
3m
12m
(2)
26cm
17cm
23cm
222
1234 ++=d
md 13169 ==
222
231726 ++=d
cmd 65.381494 ≈=

12. Using the Pythagorean Theorem in Three Dimensions
Find the length of the space diagonal of a
6 cm by 8 cm by 10 cm rectangular prism
Substitute
Simplify

13. Using the Pythagorean Theorem in Three Dimensions
Find the height of a rectangular prism with a 12 in. by 7 in.
base and a space diagonal of 15 in.
225 = 144 + 49 + h2
h2
= 32
Substitute
Square both sides of the equation.
Simplify.
Solve for h2
.
Take the square root of both sides.