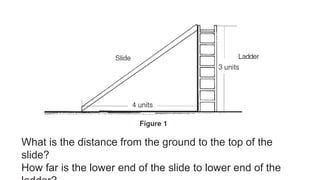
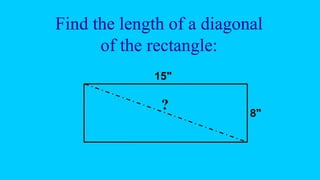
The document explains how to use the Pythagorean theorem to solve problems involving right triangles. It provides examples of using the theorem to calculate the length of a ladder/slide, the distance a diver must swim, the length of a kite string, and the distance traveled from driving directions. The theorem states that for any right triangle, the square of the hypotenuse (the side opposite the right angle) equals the sum of the squares of the other two sides. The document walks through setting up and solving examples using the formula a2 + b2 = c2, where a and b are the legs and c is the hypotenuse.

2. a
b
c
2
2
2
c
b
a 


3. What angle is formed by the ladder and the
ground?

4. What is the distance from the ground to the top of the
slide?
How far is the lower end of the slide to lower end of the

5. But how can we compute the length of the
slide?
We can do this by using the Pythagorean theorem given
the length of the ladder and the distance from the lower
end of the slide to the lower end of the ladder.

6. This is a right triangle:

7. We call it a right triangle
because it contains a
right angle.

8. The measure of a right
angle is 90o
90o

9. The little square
90o
in the
angle tells you it is a
right angle.

10. About 2,500 years ago, a
Greek mathematician named
Pythagorus discovered a
special relationship between
the sides of right triangles.

11. Pythagorus realized that if
you have a right triangle,
3
4
5

12. and you square the lengths
of the two sides that make
up the right angle,
2
4
2
3
3
4
5

13. and add them together,
3
4
5
2
4
2
3 2
2
4
3 

14. 2
2
4
3 
you get the same number
you would get by squaring
the other side.
2
2
2
5
4
3 

3
4
5

15. Is that correct?
2
2
2
5
4
3 

?
25
16
9 

?

16. It is. And it is true for any
right triangle.
8
6
10
2
2
2
10
8
6 

100
64
36 


17. The two sides which
come together in a right
angle are called

18. The two sides which
come together in a right
angle are called

19. The two sides which
come together in a right
angle are called

20. The lengths of the legs are
usually called a and b.
a
b

21. The side across from the
right angle
a
b
is called the

22. And the length of the
hypotenuse
is usually labeled c.
a
b
c

23. The relationship Pythagorus
discovered is now called
The Pythagorean Theorem:
a
b
c

24. The Pythagorean Theorem
says, given the right triangle
with legs a and b and
hypotenuse c,
a
b
c

25. then
a
b
c
.
2
2
2
c
b
a 


26. LETS
WATCH
THIS
VIDEOS

27. STEP 1
Identify the hypotenuse and the legs of the triangle.
The hypotenuse c is the side opposite to the right
angle. Therefore, c = length of the slide.
The two legs of the triangle are represented by the
ladder and the ground. Therefore, a = length of the
ladder and b = distance between the lower end of the
slide and the lower end of the ladder.

28. STEP 2
Use the formula derived from the
Pythagorean theorem. If c is the hypotenuse
of the right triangle and a and b are its legs,
we will then
have:
𝑐2 = 𝑎2 + 𝑏2

29. STEP 3
Substitute the given values to the variables (a, b and c) in the
formula and solve for the unknown. Recall that:
a = length of the ladder = 3 units
b = distance from the bottom of the ladder to the bottom of the
slide = 4 units
c = length of the slide
𝑐2
= 𝑎2
+ 𝑏2
𝑐² = 42
+ 32
𝑐² = 16 + 9
𝑐² = 25

30. STEP 4 To get the final answer, we need to remove
the exponent of the term on the right. We do this by
getting the square roots of both terms on the right and
left as in:
𝑐2 = 25
c = 5 units
So, the lenght of the slide or the hypotenuse of the
right triangle is 5 units long.

31. How far must a diver swim to be 12 meters below
sea level (as shown in the figure below)?

32. STEP 1
Identify the hypotenuse and the legs of the
triangle.
The distance that the diver must travel is the
side opposite the right angle. This means
that the said distance represents the
hypotenuse of the triangle.
Therefore c = distance that the diver must
travel.
The two legs of the triangle are represented
by the distance below sea level and the
distance between the diver at Point C and
Point B below sea level. Therefore, a =
distance below sea level, and b = distance
between the diver at Point C and Point B.

33. STEP 2
Use the formula derived from the
Pythagorean theorem.
𝑐2
= 𝑎2
+ 𝑏2

34. STEP 3
Substitute the given values to the variables in the formula and solve
for the unknown.
Recall that:
a = distance below sea level = 12 meters
b = distance between the diver at Point C to Point B = 5 meters
c = distance that the diver must travel
𝑐2
= 𝑎2
+ 𝑏2
𝑐² = 122
+ 52
𝑐² = 144 + 25
𝑐² = 169

35. STEP 4 Get the final answer by:
𝑐2 = 169
𝑐 = 13 𝑢𝑛𝑖𝑡𝑠
The diver must therefore travel or the hypotenuse of
the right triangle = 13 meters.

36. A boy is flying a kite at a
height of 17 meters from
the ground. The boy is
holding the string of the
kite 12 meters away from
the point directly below the
kite. If the height of the boy
is 1 meter, how long is the
string of the kite?

37. STEP 1
Identify the hypotenuse and the legs of the triangle.
The length of the string of the kite to the boy is the side opposite the
right angle or the hypotenuse of the triangle.
The two legs of the triangle are represented by the height of the kite
from the ground minus the height of the boy and the distance of the
boy from Point B.
Therefore a = distance of the boy from Point B and b = height of the
kite minus the height of the boy.

38. STEP 2
Use the formula derived from the
Pythagorean theorem.
𝑐2
= 𝑎2
+ 𝑏2

39. STEP 3
Substitute the given values to the variables in the formula and solve
for the unknown.
Recall that:
a = distance of the boy from Point B: ____ m
b = height of the kite minus the height of the boy:
____ to ____ = ____ m
c = length of the string
If we substitute the values in the formula, we then have:
𝑐2
= 𝑎2
+ 𝑏2
= ____________
= ____________
= ____________
17 1 16
12
𝒄𝟐
= 𝟏𝟐𝟐
+ 𝟏𝟔𝟐
𝒄𝟐
= 𝟏𝟒𝟒 + 𝟐𝟓𝟔
𝒄𝟐
= 𝟒𝟎𝟎

40. STEP 4
Get the final answer by:
𝑐2 =
𝑐 = _____
The length of the string is ______ m.
400
20
20

41. You can use The Pythagorean
Theorem to solve many kinds
of problems.
Suppose you drive directly
west for 48 miles,
48

42. Then turn south and drive for
36 miles.
48
36

43. How far are you from where
you started?
48
36
?

44. 482
Using The Pythagorean
Theorem,
48
36
c
362
+ = c2

45. Why?
Can you see that we have a
right triangle?
48
36
c
482
362
+ = c2

46. Which side is the hypotenuse?
Which sides are the legs?
48
36
c
482
362
+ = c2

47. 
 2
2
36
48
Then all we need to do is
calculate:

1296
2304

3600 2
c

48. And you end up 60 miles from
where you started.
48
36
60
So, since c2
is 3600, c is 60.
So, since c2
is 3600, c is

49. Find the length of a diagonal
of the rectangle:
15"
8"
?

50. Find the length of a diagonal
of the rectangle:
15"
8"
?
b = 8
a = 15
c

51. 2
2
2
c
b
a 
 2
2
2
8
15 c

 2
64
225 c

 289
2

c 17

c
b = 8
a = 15
c

52. Find the length of a diagonal
of the rectangle:
15"
8"
17

53. Practice using
The Pythagorean Theorem
to solve these right triangles:

54. 5
12
c = 13

55. 10
b
26

56. 10
b
26
= 24
(a)
(c)
2
2
2
c
b
a 

2
2
2
26
10 
 b
676
100 2

 b
100
676
2


b
576
2

b
24

b

57. 12
b
15
= 9