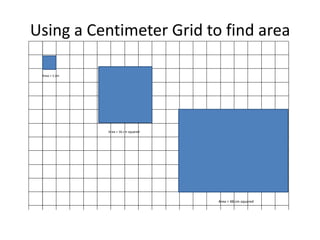
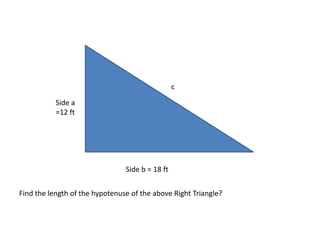
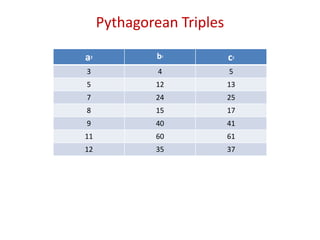
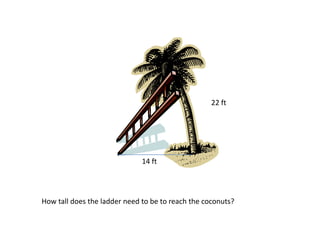
This document provides instruction on using the Pythagorean theorem to solve for unknown sides of right triangles. It defines key terms like hypotenuse and legs, shows the Pythagorean theorem formula, and provides examples of using it to find the length of unknown sides. Historical context is given about Pythagoras and that other ancient cultures also understood this relationship between triangle sides. Word problems are worked through as practice applications of the theorem.

1. CSO: M.O.8.4.3Objective:Students will solve right triangle problems where the existence of triangles is not obvious using the Pythagorean Theorem.

2. Legs – The sides that form the Right (90⁰) angle.Hypotenuse – The side opposite the right angle, it is the longest side of the triangle.Converse – reversing the parts.Helpful Vocabulary

3. Pythagorean TheoremDescribes the relationship between the lengths of the legs and the hypotenuse for any right triangleHypotenuseLeg 1Leg 2

4. IN WORDS AND SYMBOLSIn a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the length c2 = a2 + b2

5. Who is Pythagoras?

6. Born in Samos (Island in Aegean Sea)Around 570 - 495 BC

7. Greek Philosopher, mathematician, and Mystic

9. ProofsFirst Video ProofSecond Video ProofThird Video Proof

10. Historical NoteWhile we call it Pythagoras‘ Theorem, it was alsoknown by Indian, Greek, Chinese and babylonian mathematicians well before he lived !

11. Using a Centimeter Grid to find areaArea = 1 cmArea = 16 cm squaredArea = 48 cm squared

12. 3-4-5 RuleThis rule is used to check for the existence of a Right corner.Simply Stated:The measure of any side of 3 units, plus the next side of 4 units has to have a diagonal side of 5 units.

13. 3-4-5 Rule ExpandedThis is the 3-4-5 Rule3 squared is 94 squared is 169+16 = 25Square Root of 25 is 5Make a ConjectureIf the length of one side is 6 andLength of the next side is 8,What would be the length of the longest side if this was a Right Triangle and 6 and 8 were the two shorter sides?10

14. The answer is 15 since we will not have a negative side to the triangle

15. Now let’s try a problem together

16. cSide a =12 ftSide b = 18 ftFind the length of the hypotenuse of the above Right Triangle?

17. Start withc2 = a2 + b2

18. Fill in with knownsc2 = a2 + b2c2 = (12)2 + (18)2

19. Square the sidesc2 = 144 + 324Addc2 = 468

20. Find the Square Root of Both Sides√c2 = √468Round c = 21.63

21. If you reverse the parts of the pythagorean theorem, you have formed itsConverse, and it is also true

22. Funny Break

23. Pythagorean Triples

24. Irrational numbers and PythagorasAn irrational number is a number that cannot be expressed as the quotient a/b where a and b are integers and b ≠ 0Every square root of an imperfect square is an irrational number.Example:√10 = 3.1622776……..This number continues indefinitely with no repetition

25. Problems to tryc2= a2 + b2c2 = 24yds2 + 18yds2c2 = 576 + 324c2 = 900c = 30b2 = c2 - a2b2 = 82 - 32b2 = 64 – 9b2 = 55b= 7.42a2 = c2- b2a2 = 20cm2 - 17cm2a2 = 400 - 289a2 = 111a = 10.54

26. Answer to this problem using Pythagoras is 8ft

27. 22 ft14 ftHow tall does the ladder need to be to reach the coconuts?

28. Hope you learned something about Pythagoras and his theorem.

29. ReferencesWho2 Biography. Copyright © 1998-2010 by Who2, LLC. All rights reserved. See the Pythagoras biography from Who2. Pierce, Rod. "Math is Fun - Maths Resources" Math Is Fun. Ed. Rod Pierce. 19 Apr 2010. 1 Oct 2010 http://www.mathsisfun.com/ http://www.glencoe.com/ose/showbook.php