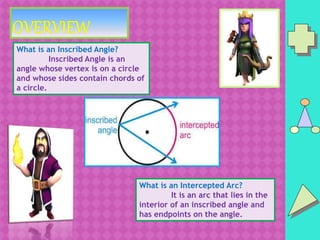
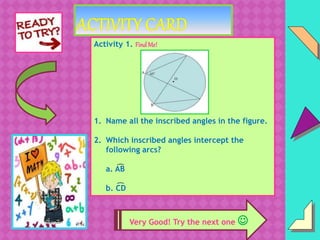
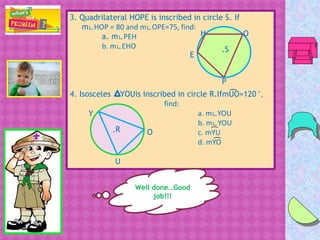
The document discusses inscribed angles and intercepted arcs, explaining that the measure of an inscribed angle is equal to half the measure of its intercepted arc. It provides examples of applying this concept to find unknown angle measures. Several activities are included for students to practice identifying, measuring, and applying properties of inscribed angles and intercepted arcs.

1. by: Hilda D.
Baquilan Resettlement High School

2. LEAST MASTERED SKILLS:
Inscribed Angles and Intercepted Arcs
SUB TASKS:
1. Identify inscribed angles and their
intercepted arcs
2. Apply the key concept of inscribed
angles and intercepted arc
3. Solve real-life problems involving
inscribed angles and intercepted
arcs

3. What is an Inscribed Angle?
Inscribed Angle is an
angle whose vertex is on a circle
and whose sides contain chords of
a circle.
What is an Intercepted Arc?
It is an arc that lies in the
interior of an inscribed angle and
has endpoints on the angle.

4. I
If an angle is inscribed in a
circle, then the measure of
the angle equals one-half
the measure of its
intercepted arc.
C
To check, m∟ABC=½ mAC
=½ (86 ̊)
=43 ̊
A
B
86 ̊43 ̊
͡

5. If two inscribed angles of a
circle intercept congruent
arcs or the same arc, then
the angles are congruent.
C
D
In the figure ∟CAD and ∟CBD
intercept CD.
Therefore, m∟CAD=m∟CBD.
If m∟CAD=45 ̊then m∟CBD=45 ̊.
͡

6. If an inscribed angle
of a circle intercepts
a semicircle, then
the angle is a right
angle.
Then m∟ABC=90 ̊. Let’s try apply it to find x ̊. The
triangle angle sum theorem explains that………….
m∟A +m∟B +m∟C = 180 ̊
Substituting the value, 50 ̊+ 90 ̊ + x ̊ = 180 ̊
140 ̊ + x ̊ = 180 ̊
x ̊= 180 ̊-140 ̊
x ̊ = 40 ̊

7. If a quadrilateral is inscribed in a
circle, then its opposite angles are
supplementary.
Using the figure, to find the m∟F it will
be:
m∟D = m∟F
85 ̊= m∟F

8. Activity 1. FindMe!
1. Name all the inscribed angles in the figure.
2. Which inscribed angles intercept the
following arcs?
a. AB
b. CD
C
D
Very Good! Try the next one 
͡
͡

9. Activity 2. Let’sPractice!
1. Given Circle with circle indicated. Find x.
Choose:
____ 36
____ 54
____ 90
____ 108

10. 2. Given the diameter. Find x.
Choose:
_____ 45
_____ 60
_____ 90
_____ 180

11. 3. Given the diameter. Find x.
Choose:
____ 28
____ 56
____ 62
____ 124

12. Activity 3. MeasureMe!
1. If m∟A = 45 ̊, find:
a. m∟B, why?
b. mCD, why?
2. If m AB = 30 ̊, find:
a. m∟1, why?
b. m∟2, why?
͡
1
2
͡
C
D
Wow, good job……try the next 

13. Y
You can do
this 
Activity 4. Half, Equalor Twice As?
1. Which inscribed angles are congruent?
Why?
2. If m∟CBD=54, what is the measure of CD?
3. If m∟ABD=5x+3 and m∟DCA=4x+10, find
a. the value of x c. m∟DCA
b. m∟ABD d. mAD
4. If m∟BDC=6x-4 and mBC=10x+2, find:
a. the value of x c.mBC
b. m∟BDC d. m∟BAC
E
D
C
B
A
͡
͡
͡
͡
Very good! Now you’re ready 

14. I believe I
can do
this…
Direction: Use the given figures to answer the
following.
1. CAR is inscribed in circle E. If m∟C=80 and
mRC= 150, find:
a. mAR b. mAC c. m∟A d. m∟R
2. HD is a diameter of circle O.
If mRD = 70 ̊, find:
a. m∟H c. m∟R
b. m∟D d. mRH
e. mHD
.E
C
A
R
͡
͡ ͡
͞
.O
R
D
H
͡
͡

15. 3. Quadrilateral HOPE is inscribed in circle S. If
m∟HOP = 80 and m∟OPE=75, find:
a. m∟PEH
b. m∟EHO
4. Isosceles YOUis inscribed in circle R.IfmUO=120 ̊,
find:
a. m∟YOU
b. m∟YOU
c. mYU
d. mYO
H
.S
E
P
O
͡
Y
O
U
.R ͡
͡
Well done…Good
job!!!

16. Activity : Take Me To Your RealWorld!
Answer the following questions.
1. What kind of parallelogram can be inscribed in a circle?
Explain.
2. There are circular garden having paths in the shape of an
inscribed square like one shown below.
a. Determine the measure of an arc
intercepted by an inscribed angle
formed by the square in the garden.
b. What is the measure of an inscribed
angle in a garden in a garden with a square?
Explain.

17. Learner’s Module , First Edition 2015 pp. 165-175
Callanta, Melvin. et al.
Geometry, Third Year pp. 205-207
Bernabe, Julieta. et al
http://www.iq.poquoson.org/math.htm
http://www.math-worksheets.org/inscribed -angles
http://www.onlinemathlearning.com/circle-theorems.html