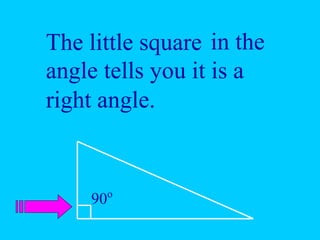
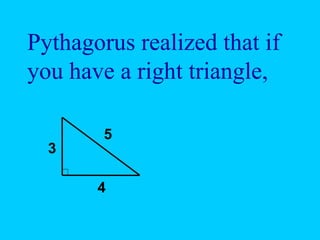
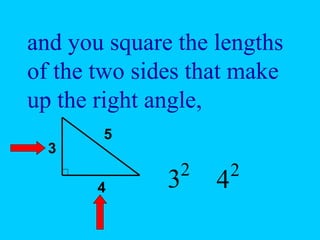
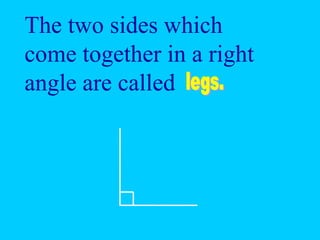
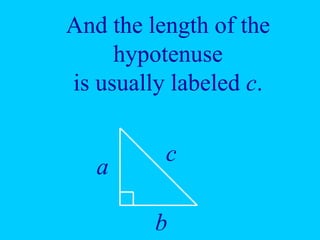
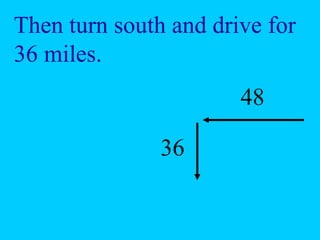
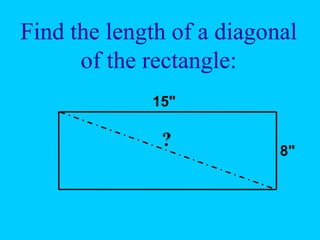
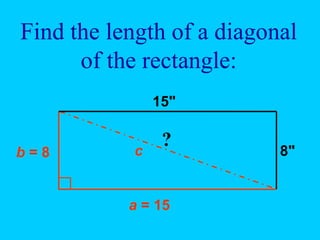
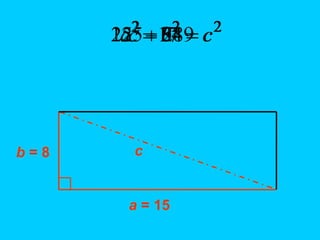
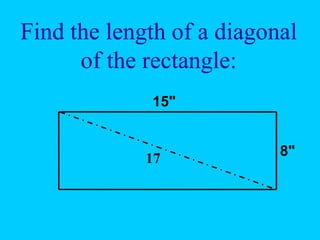
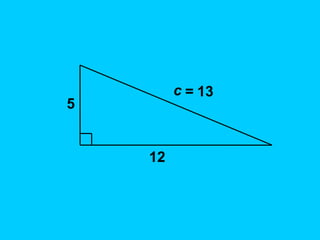
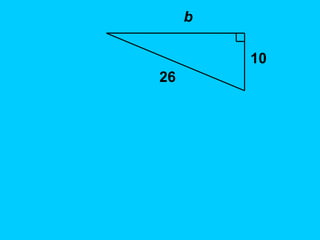
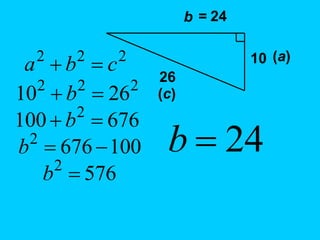
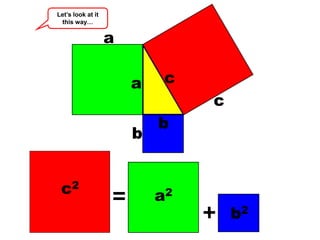
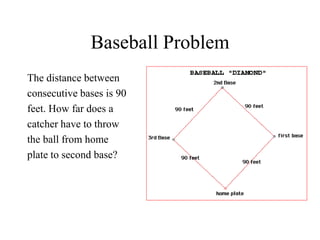
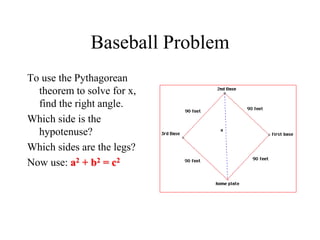
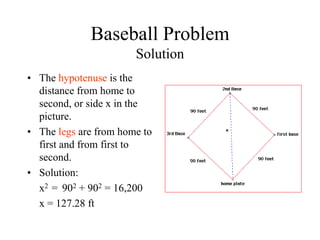
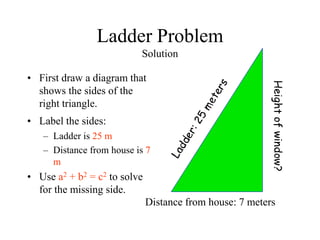
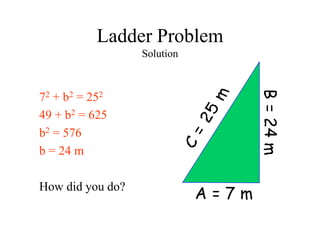
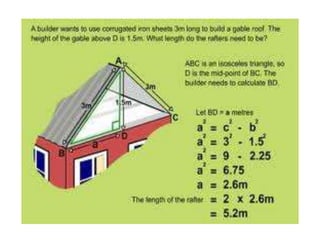
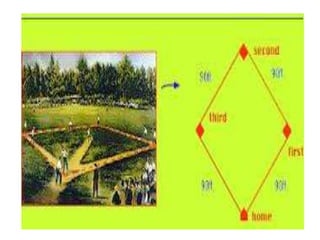
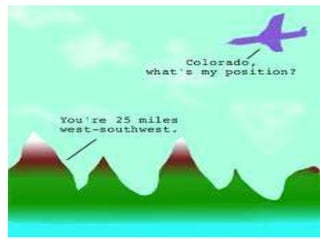
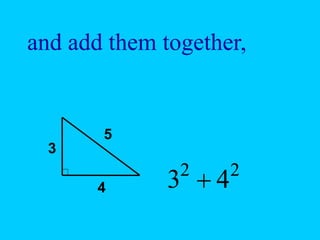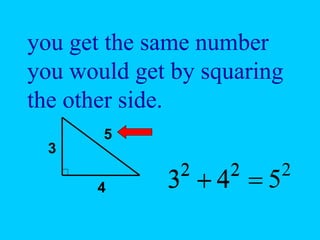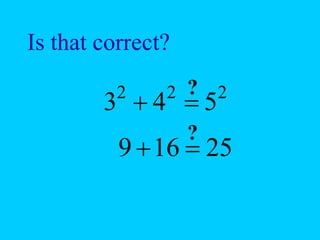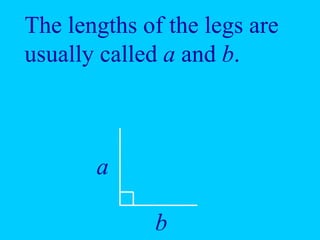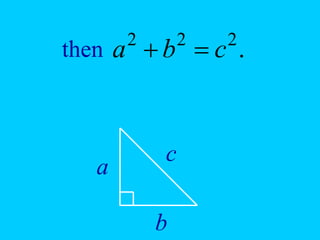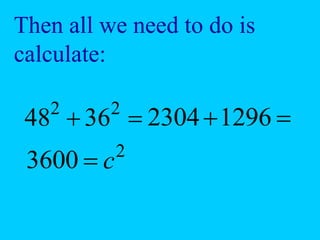The document discusses the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides (a^2 + b^2 = c^2). It provides historical context, examples of Pythagorean triplets, and practical applications through problem-solving scenarios including distances and geometry. Additionally, it covers how to use the theorem in real-life situations such as calculating lengths and measurements in right triangles.

1. Pythagorean Theorem
S. Anbalagan,
Assistant Professor of Mathematics
Thiagarajar College of Preceptors,
Madurai

2. Pythagorean Theorem

3. a
b
c
2
2
2
c
b
a 


4. Pythagoras Theorem: In a right triangle, the area of the
square on the hypotenuse is equal to the sum of the areas
of the squares of its remaining two sides.
(Hypotenuse)2=(Perpendicular)2+(Base)2
(AC)2=(CB)2+(BA)2
For Pythagorean triplets:
a2+b2=c2
a=6
b=8
c=10
∴62+82=36+64=100=102
That is a2+b2=c2
Hence 6,8,10 are Pythagorean triplets.

5. Pythagorean Theorem Essential
Questions
How is the Pythagorean Theorem used to
identify side lengths?
When can the Pythagorean Theorem be
used to solve real life patterns?

6. This is a right triangle:

7. We call it a right triangle
because it contains a
right angle.

8. The measure of a right
angle is 90o
90o

9. The little square
90o
in the
angle tells you it is a
right angle.

10. About 2,500 years ago, a
Greek mathematician named
Pythagorus discovered a
special relationship between
the sides of right triangles.

11. Pythagorus realized that if
you have a right triangle,
3
4
5

12. and you square the lengths
of the two sides that make
up the right angle,
2
4
2
3
3
4
5

13. and add them together,
3
4
5
2
4
2
3 2
2
4
3 

14. 2
2
4
3 
you get the same number
you would get by squaring
the other side.
2
2
2
5
4
3 

3
4
5

15. Is that correct?
2
2
2
5
4
3 

?
25
16
9 

?

16. It is. And it is true for any
right triangle.
8
6
10
2
2
2
10
8
6 

100
64
36 


17. The two sides which
come together in a right
angle are called

18. The two sides which
come together in a right
angle are called

19. The two sides which
come together in a right
angle are called

20. The lengths of the legs are
usually called a and b.
a
b

21. The side across from the
right angle
a
b
is called the

22. And the length of the
hypotenuse
is usually labeled c.
a
b
c

23. The relationship Pythagorus
discovered is now called
The Pythagorean Theorem:
a
b
c

24. The Pythagorean Theorem
says, given the right triangle
with legs a and b and
hypotenuse c,
a
b
c

25. then
a
b
c
.
2
2
2
c
b
a 


26. You can use The Pythagorean
Theorem to solve many kinds
of problems.
Suppose you drive directly
west for 48 miles,
48

27. Then turn south and drive for
36 miles.
48
36

28. How far are you from where
you started?
48
36
?

29. 482
Using The Pythagorean
Theorem,
48
36
c
362
+ = c2

30. Why?
Can you see that we have a
right triangle?
48
36
c
482
362
+ = c2

31. Which side is the hypotenuse?
Which sides are the legs?
48
36
c
482
362
+ = c2

32. 
 2
2
36
48
Then all we need to do is
calculate:

1296
2304

3600 2
c

33. And you end up 60 miles from
where you started.
48
36
60
So, since c2
is 3600, c is 60.
So, since c2
is 3600, c is

34. Find the length of a diagonal
of the rectangle:
15"
8"
?

35. Find the length of a diagonal
of the rectangle:
15"
8"
?
b = 8
a = 15
c

36. 2
2
2
c
b
a 
 2
2
2
8
15 c

 2
64
225 c

 289
2

c 17

c
b = 8
a = 15
c

37. Find the length of a diagonal
of the rectangle:
15"
8"
17

38. Practice using
The Pythagorean Theorem
to solve these right triangles:

39. 5
12
c = 13

40. 10
b
26

41. 10
b
26
= 24
(a)
(c)
2
2
2
c
b
a 

2
2
2
26
10 
 b
676
100 2

 b
100
676
2


b
576
2

b
24

b

42. Check It Out! Example 2
A rectangular field has a length of 100 yards and a
width of 33 yards. About how far is it from one corner
of the field to the opposite corner of the field? Round
your answer to the nearest tenth.

43. Check It Out! Example 2 Continued
1 Understand the Problem
Rewrite the question as a statement.
• Find the distance from one corner of the field to the
opposite corner of the field.
• The segment between the two corners is
the hypotenuse.
• The sides of the fields are legs, and they are 33 yards long
and 100 yards long.
List the important information:
• Drawing a segment from one corner of the field to the
opposite corner of the field divides the field into two
right triangles.

44. Check It Out! Example 2 Continued
2 Make a Plan
You can use the Pythagorean Theorem to
write an equation.

45. Check It Out! Example 2 Continued
Solve
3
a2 + b2 = c2
332 + 1002 = c2
1089 + 10,000 = c2
11,089 = c2
105.304  c
The distance from one corner of the field to the
opposite corner is about 105.3 yards.
Use the Pythagorean Theorem.
Substitute for the known variables.
Evaluate the powers.
Add.
Take the square roots of both sides.
105.3  c Round.

46. The Pythagorean Theorem
“For any right triangle,
the sum of the areas of
the two small squares is
equal to the area of the
larger.”
a2 + b2 = c2

47. "The area of the square built
upon the hypotenuse of a right
triangle is equal to the sum of the
areas of the squares upon the
remaining sides."

48. Proof

49. a
a
a2
b
b
c
c
b2
c2
Let’s look at it
this way…

50. Baseball Problem
A baseball “diamond” is really a square.
You can use the Pythagorean theorem to find
distances around a baseball diamond.

51. Baseball Problem
The distance between
consecutive bases is 90
feet. How far does a
catcher have to throw
the ball from home
plate to second base?

52. Baseball Problem
To use the Pythagorean
theorem to solve for x,
find the right angle.
Which side is the
hypotenuse?
Which sides are the legs?
Now use: a2 + b2 = c2

53. Baseball Problem
Solution
• The hypotenuse is the
distance from home to
second, or side x in the
picture.
• The legs are from home to
first and from first to
second.
• Solution:
x2 = 902 + 902 = 16,200
x = 127.28 ft

54. Ladder Problem
A ladder leans against a
second-story window of a
house.
If the ladder is 25 meters
long,
and the base of the ladder
is 7 meters from the
house,
how high is the window?

55. Ladder Problem
Solution
• First draw a diagram that
shows the sides of the
right triangle.
• Label the sides:
– Ladder is 25 m
– Distance from house is 7
m
• Use a2 + b2 = c2 to solve
for the missing side.
Distance from house: 7 meters

56. Ladder Problem
Solution
72 + b2 = 252
49 + b2 = 625
b2 = 576
b = 24 m
How did you do?
A = 7 m