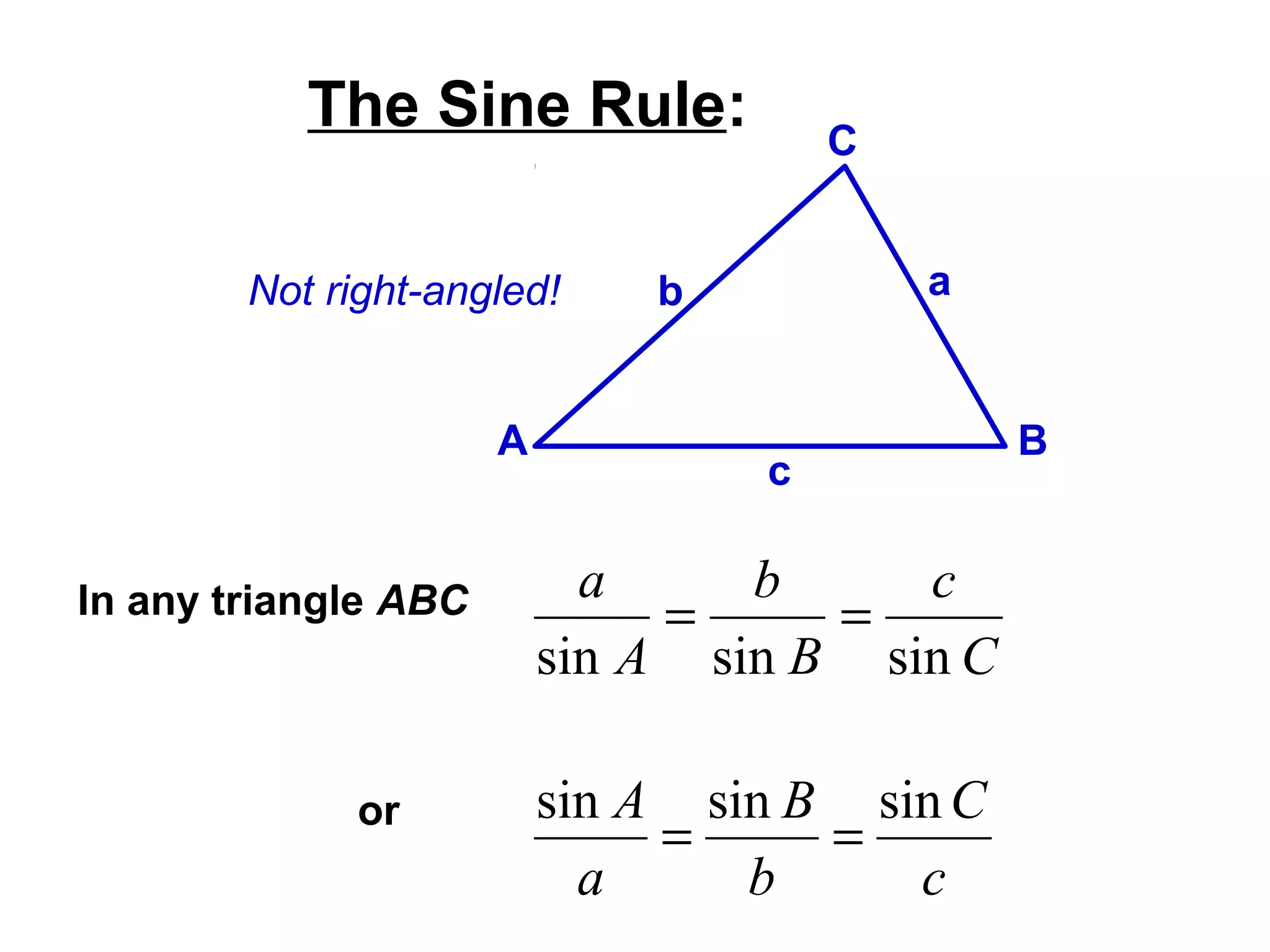
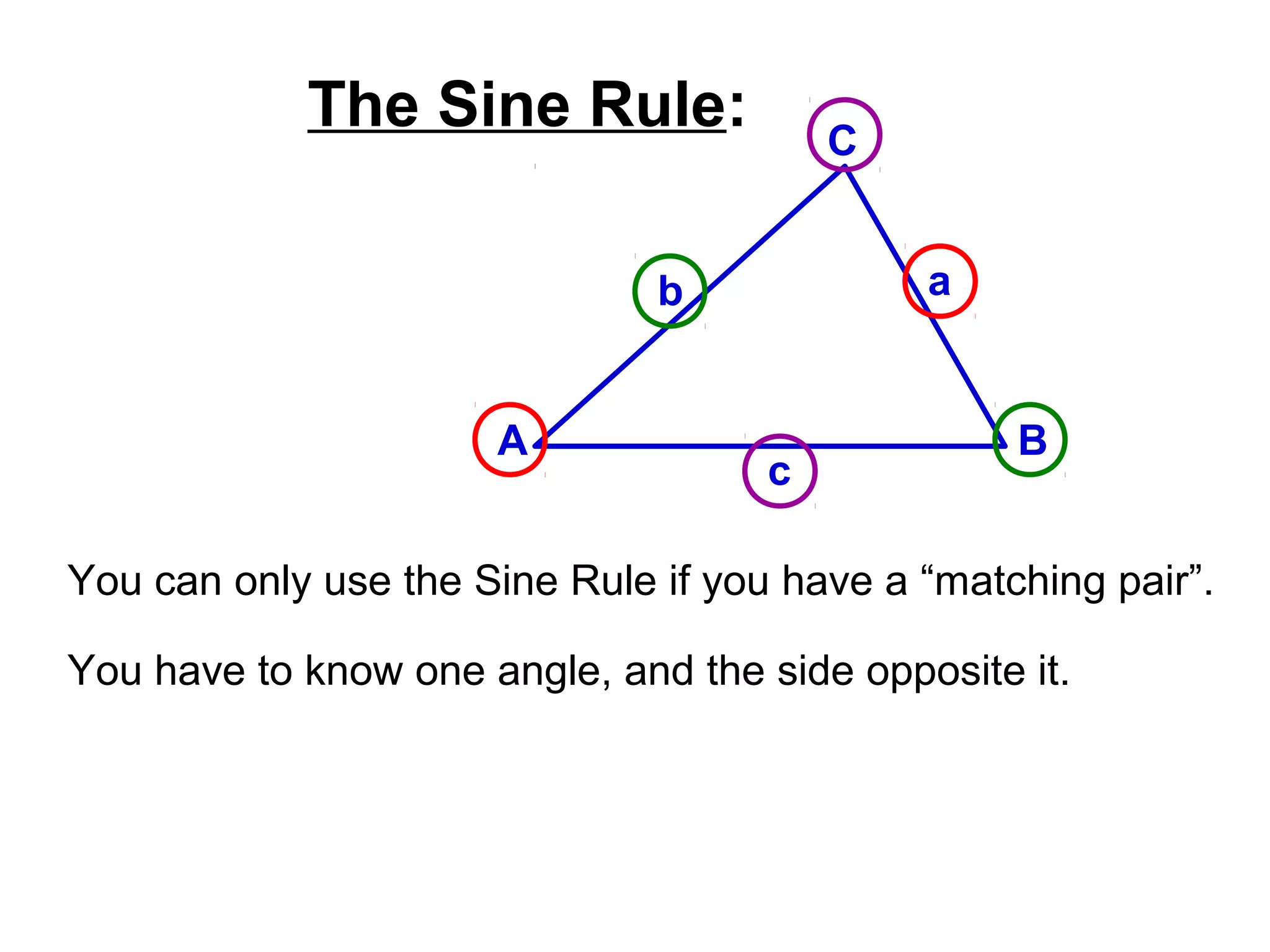
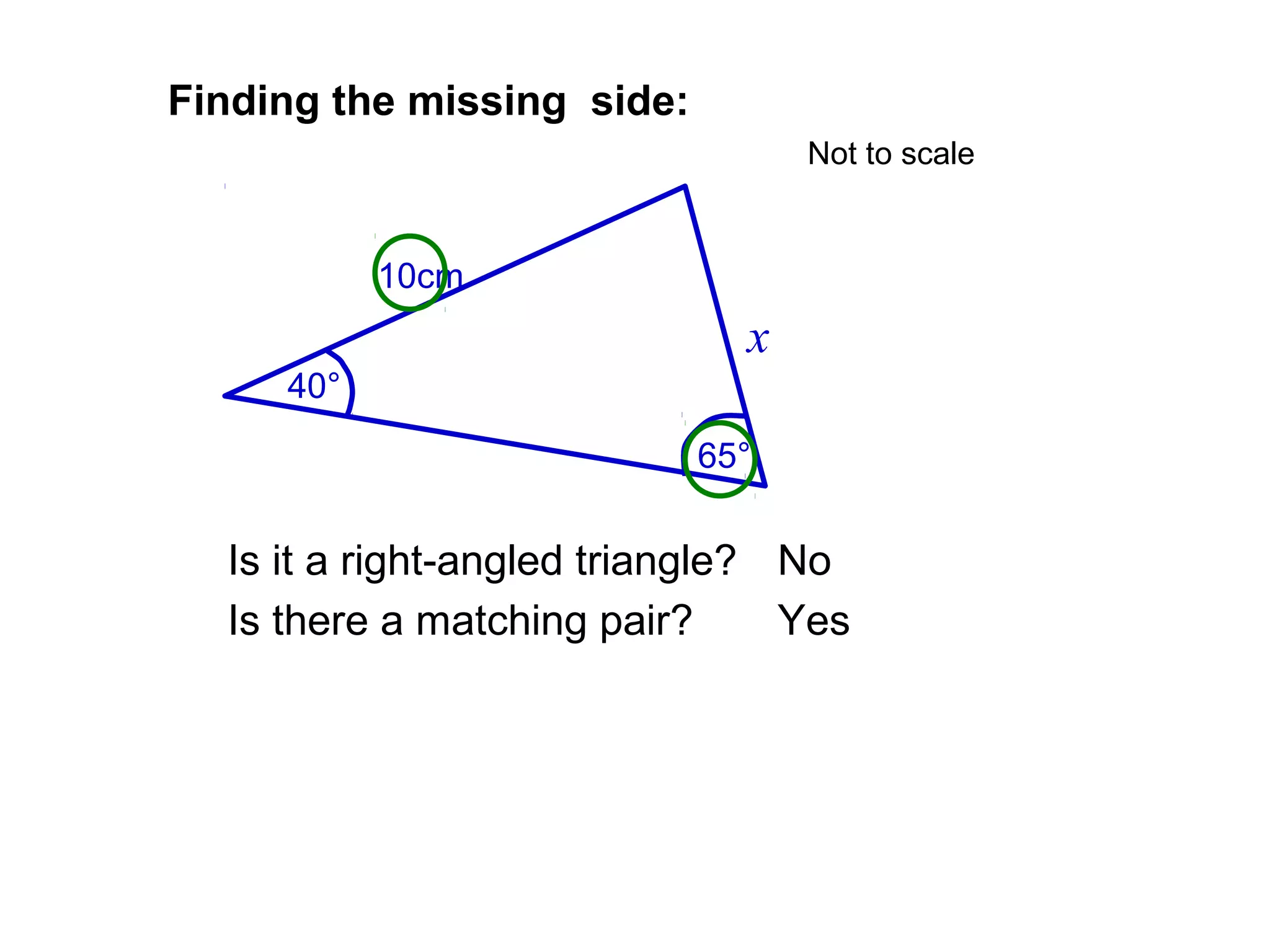
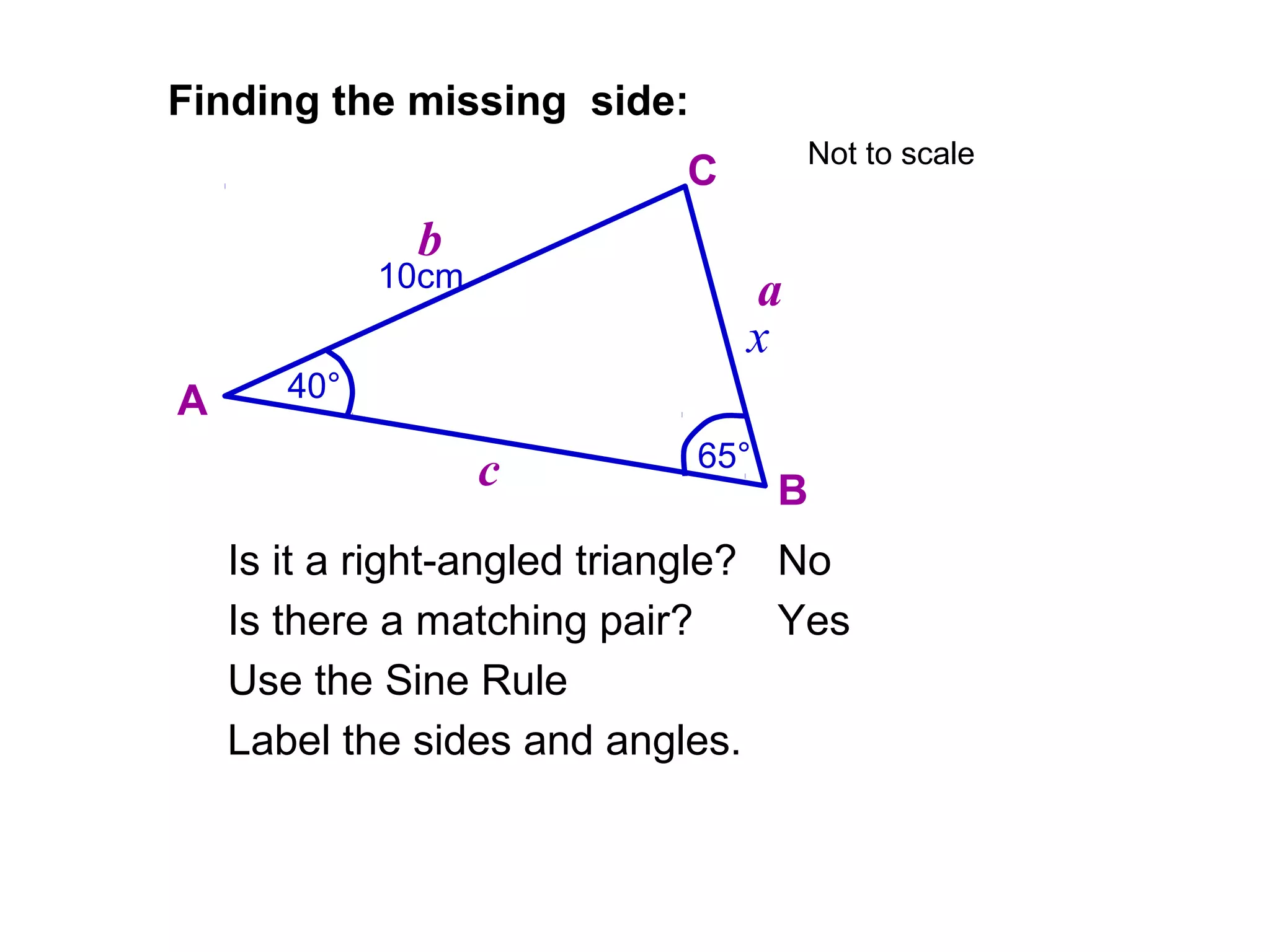
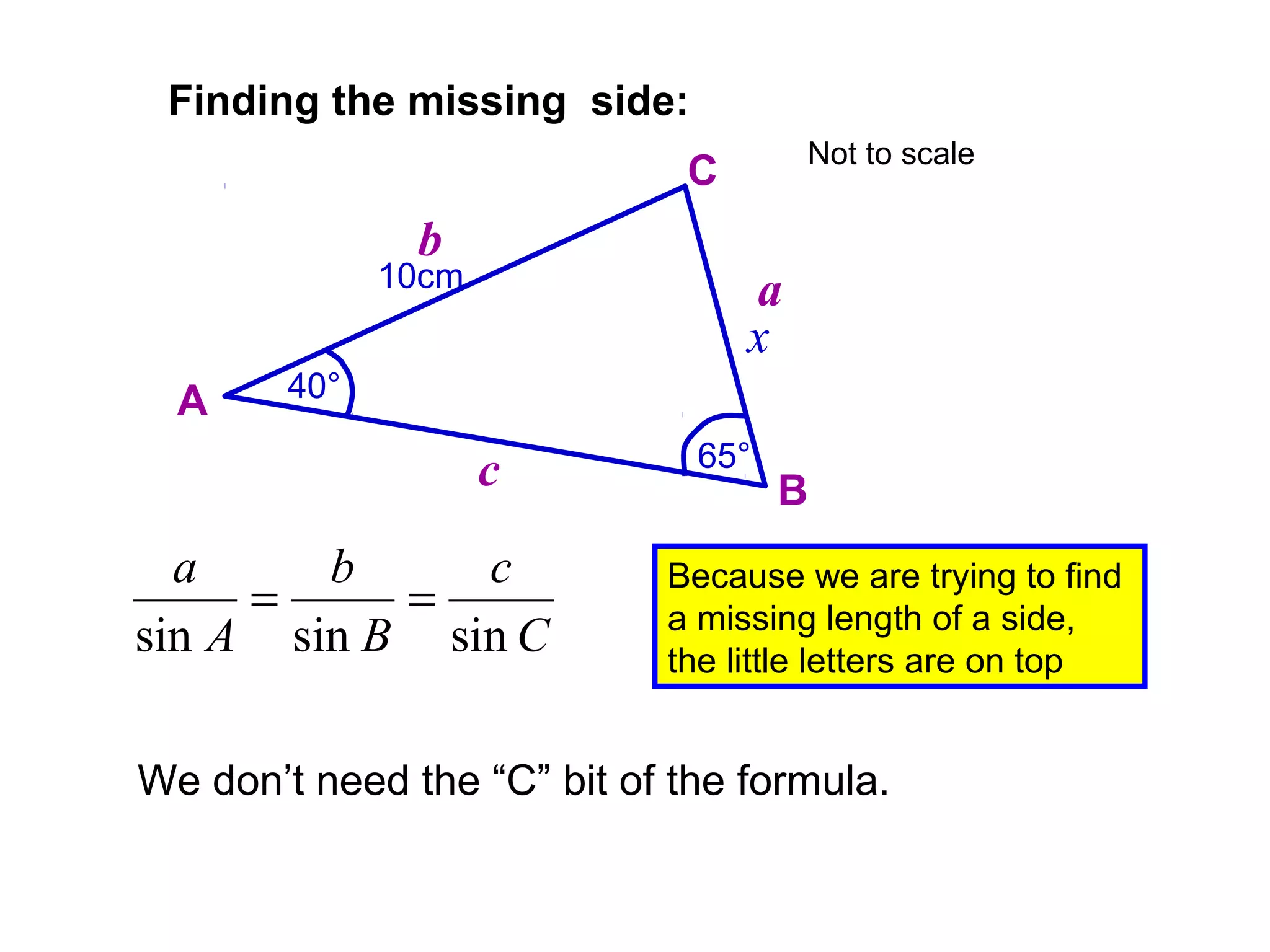
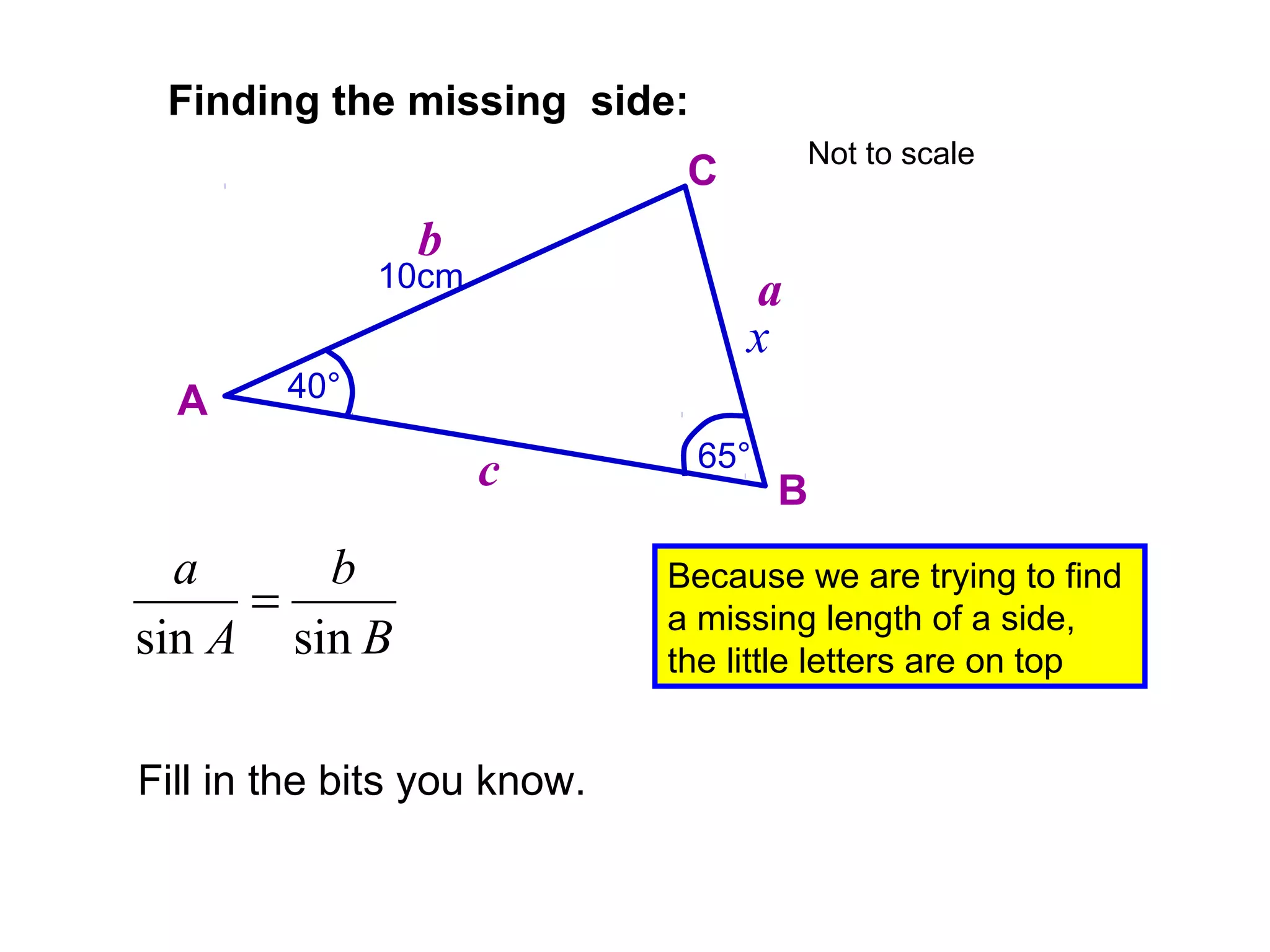
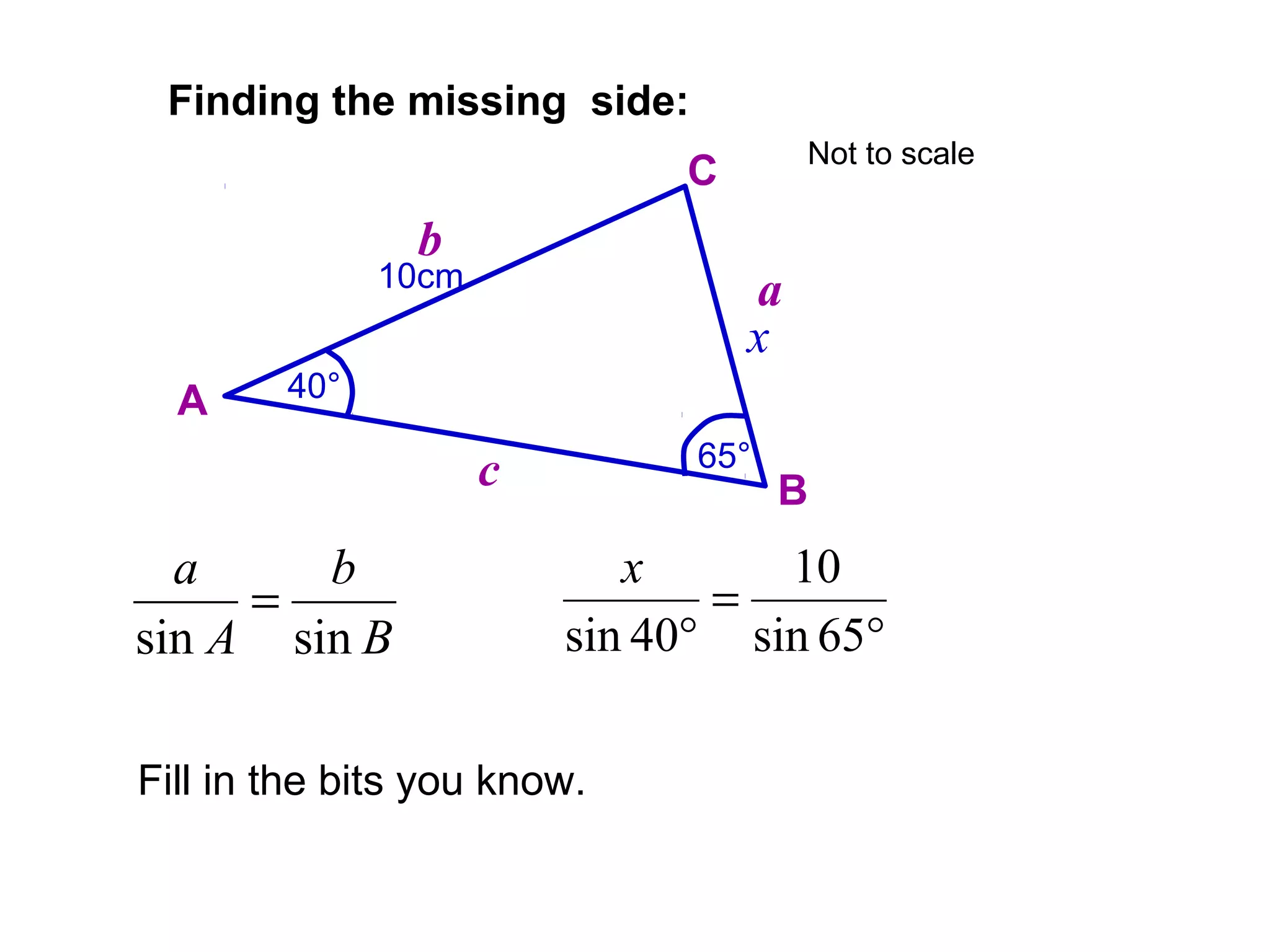
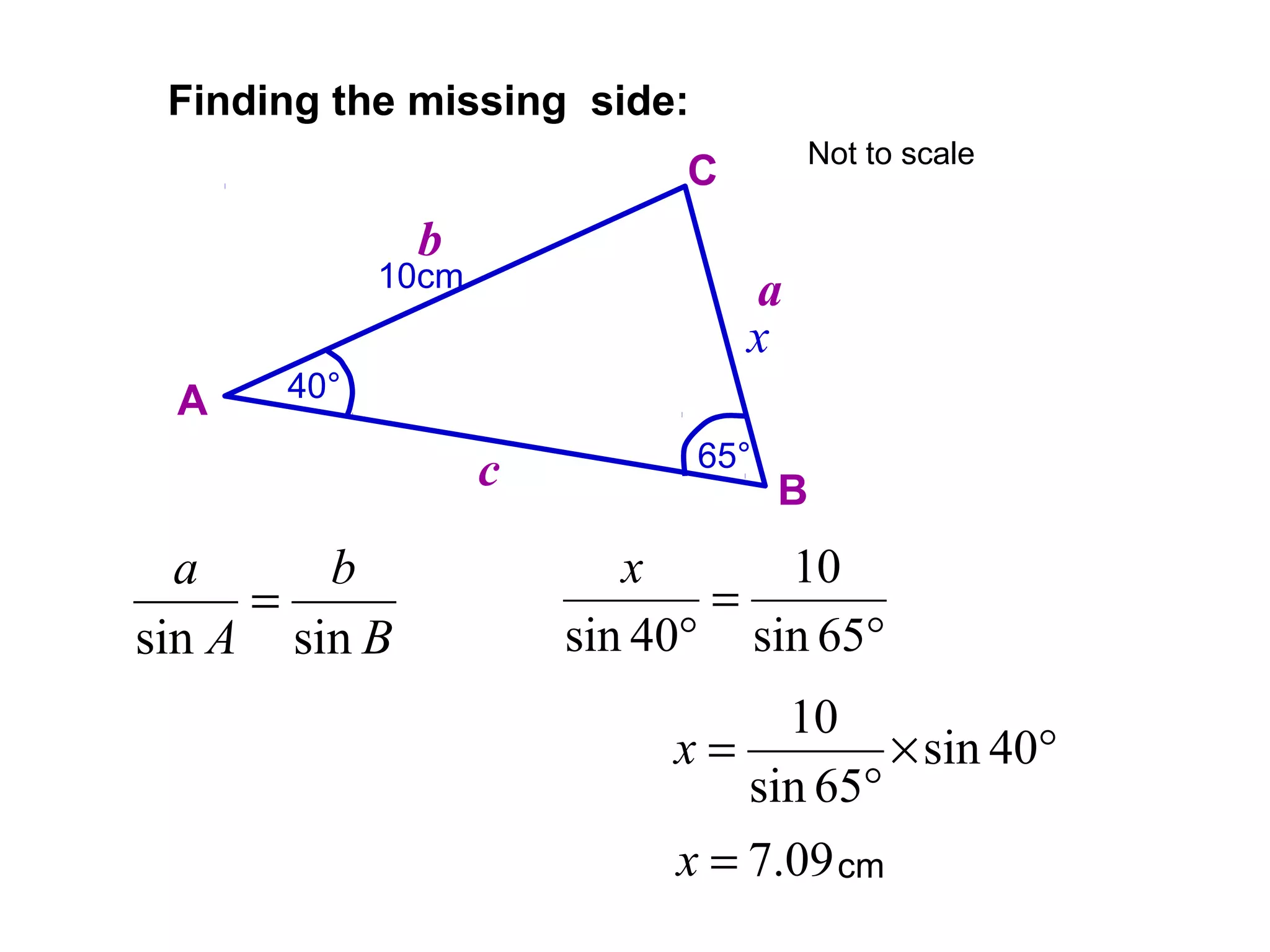
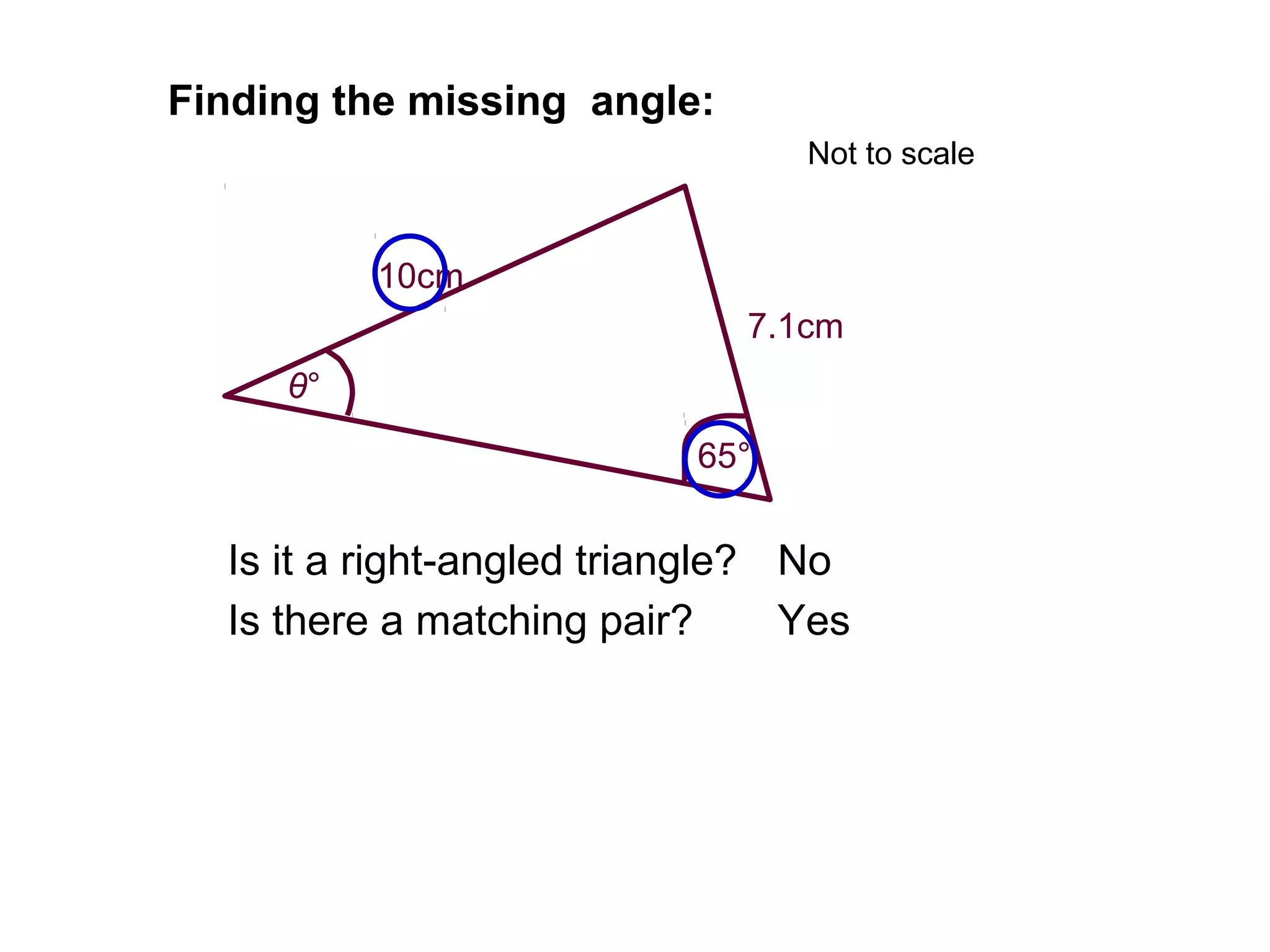
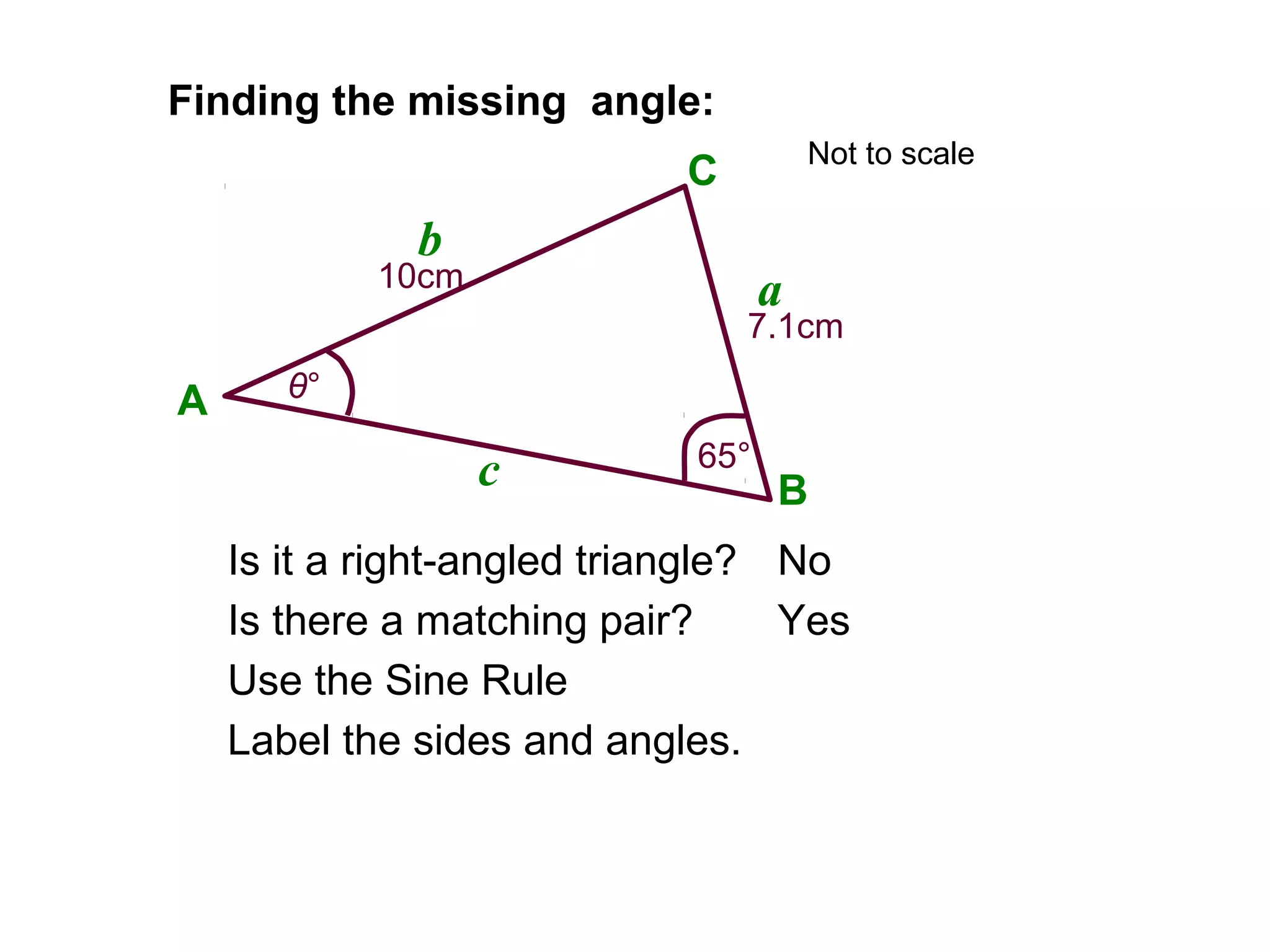
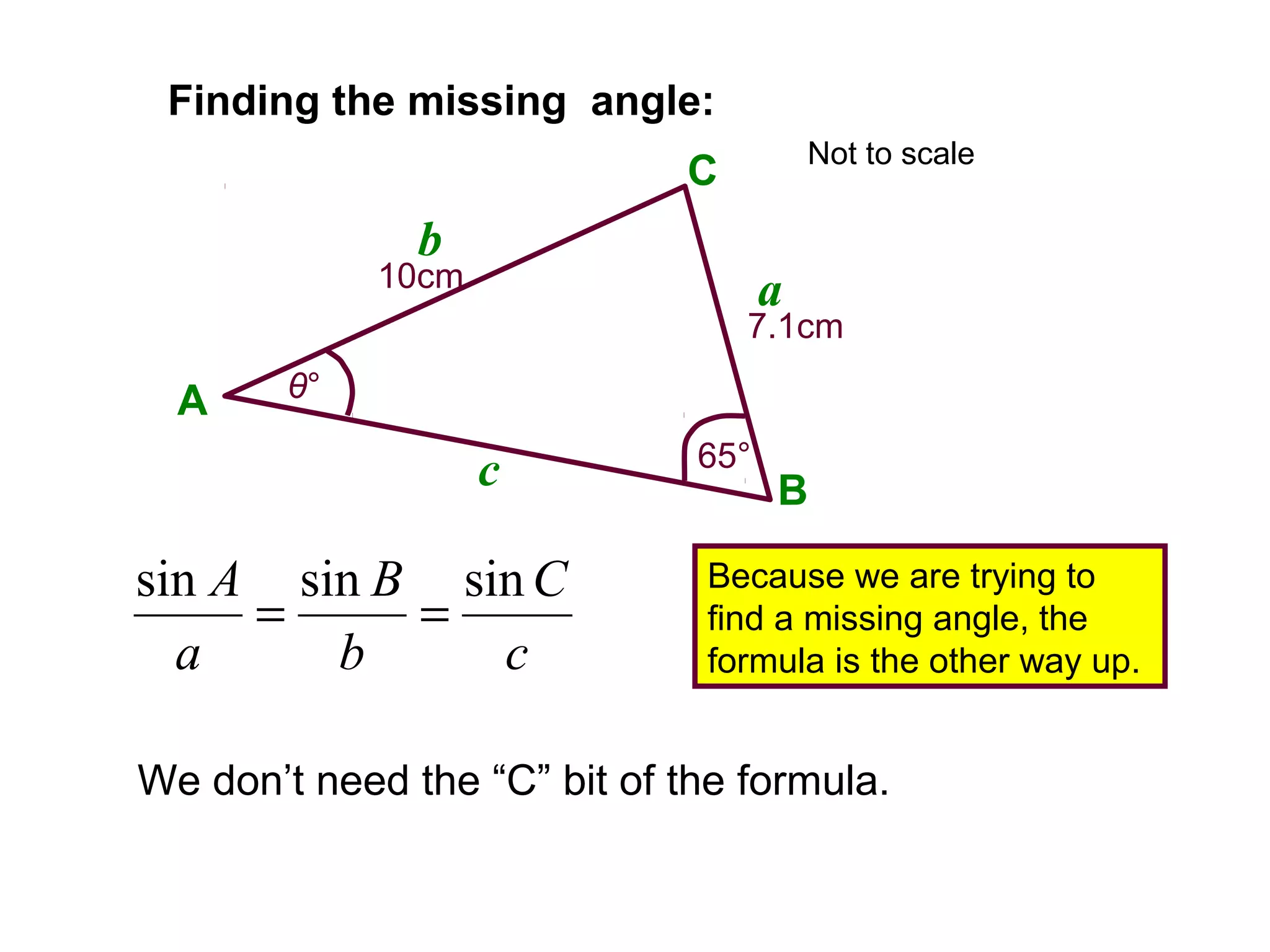
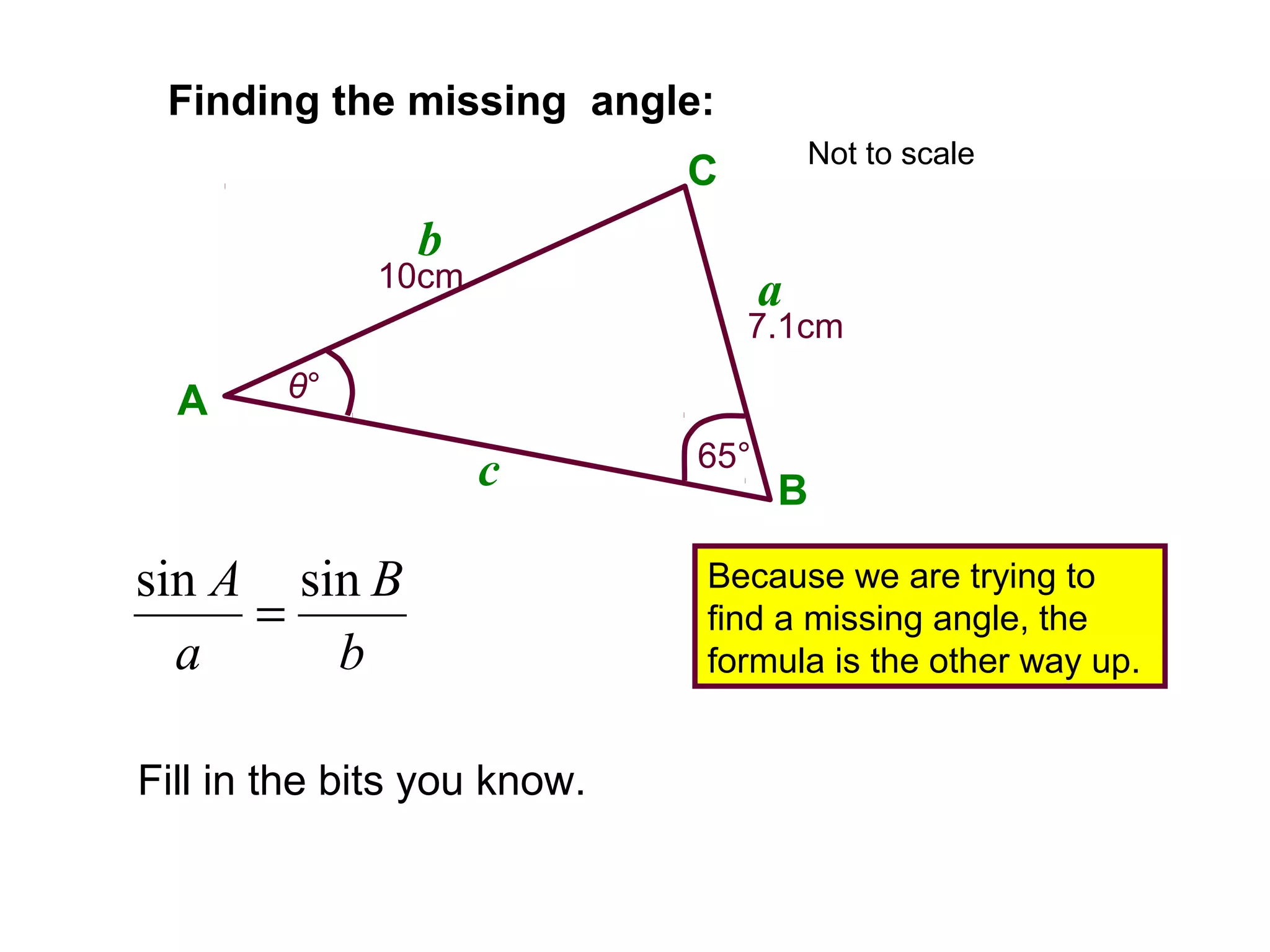
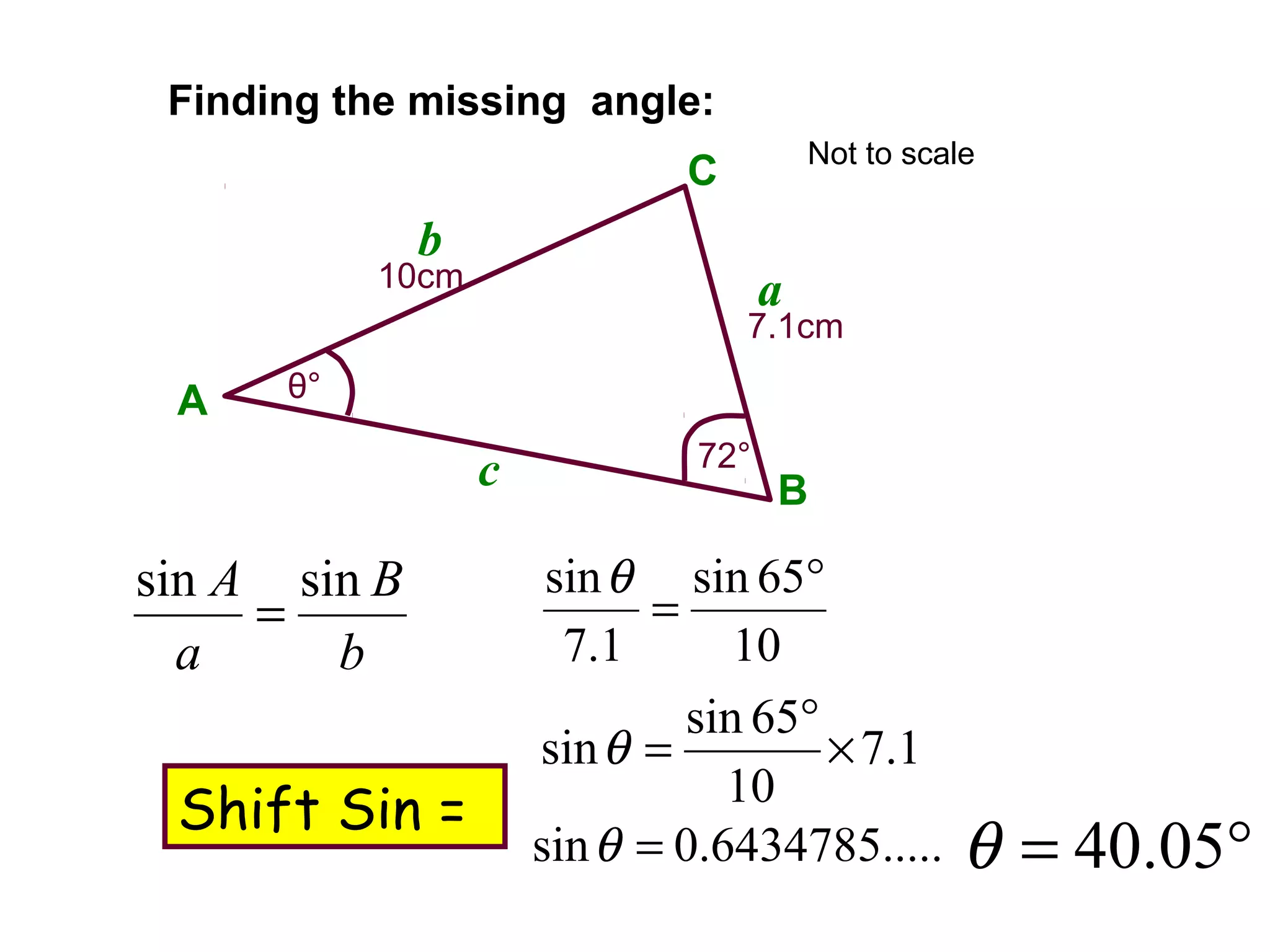
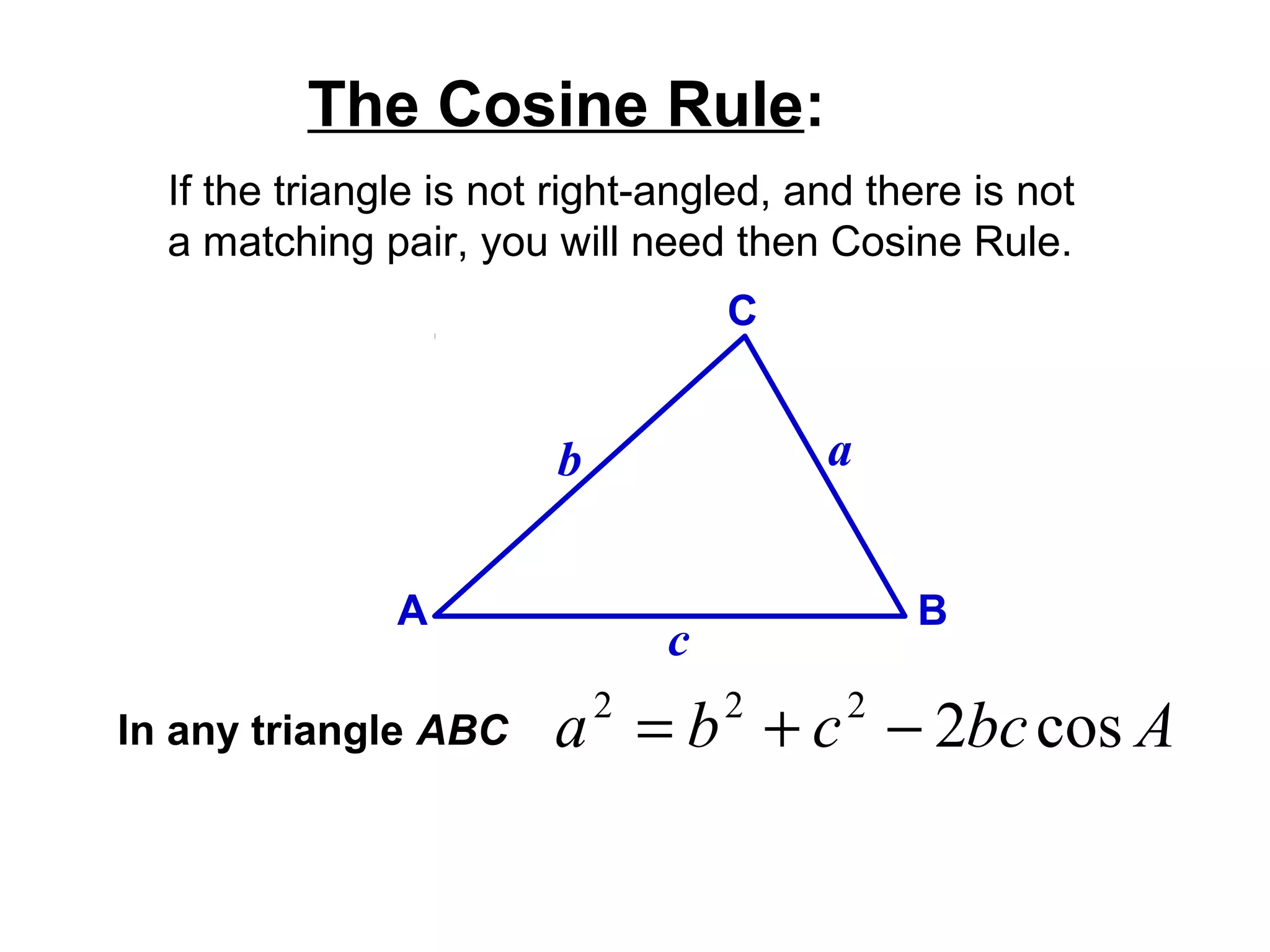
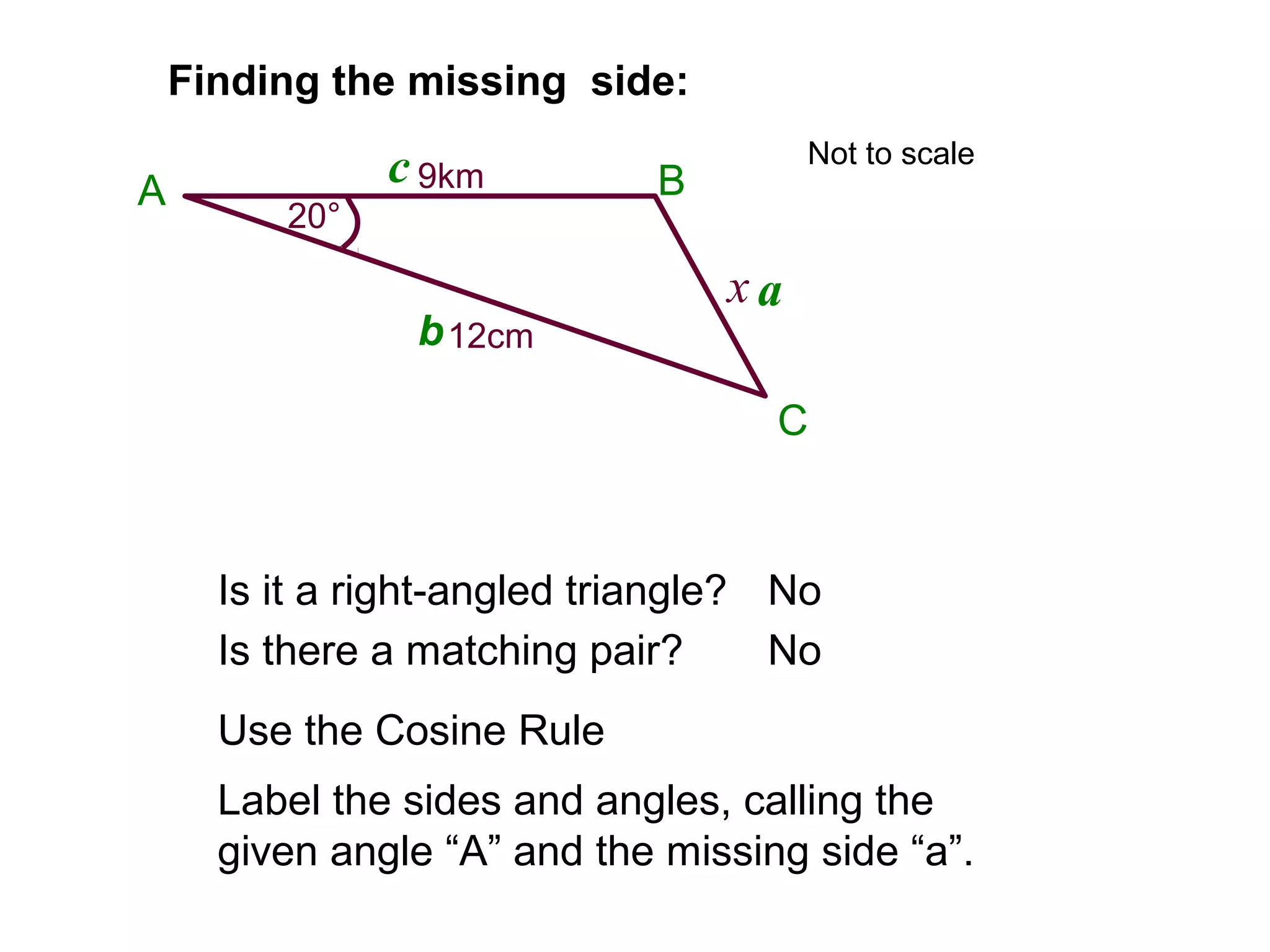
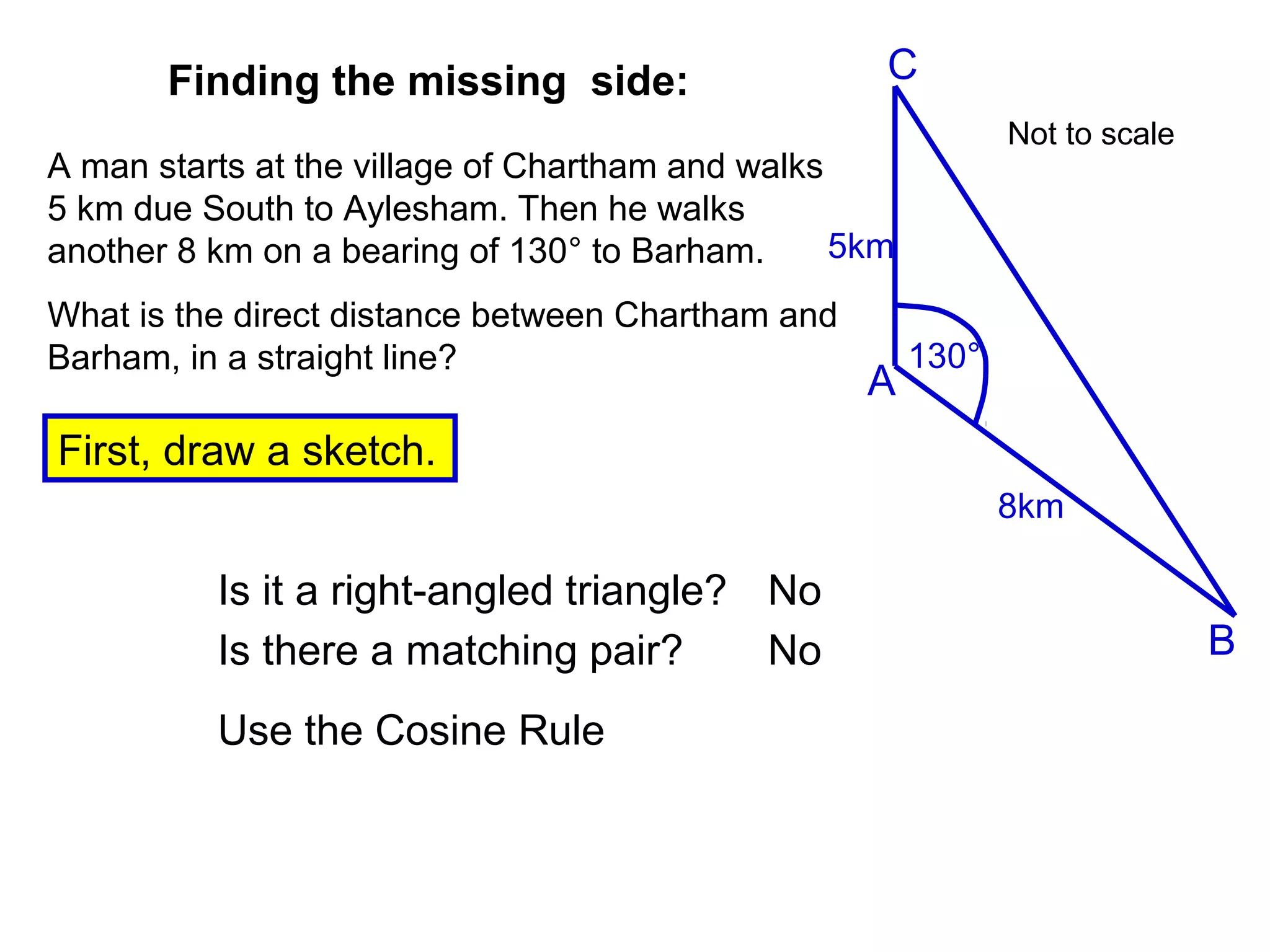
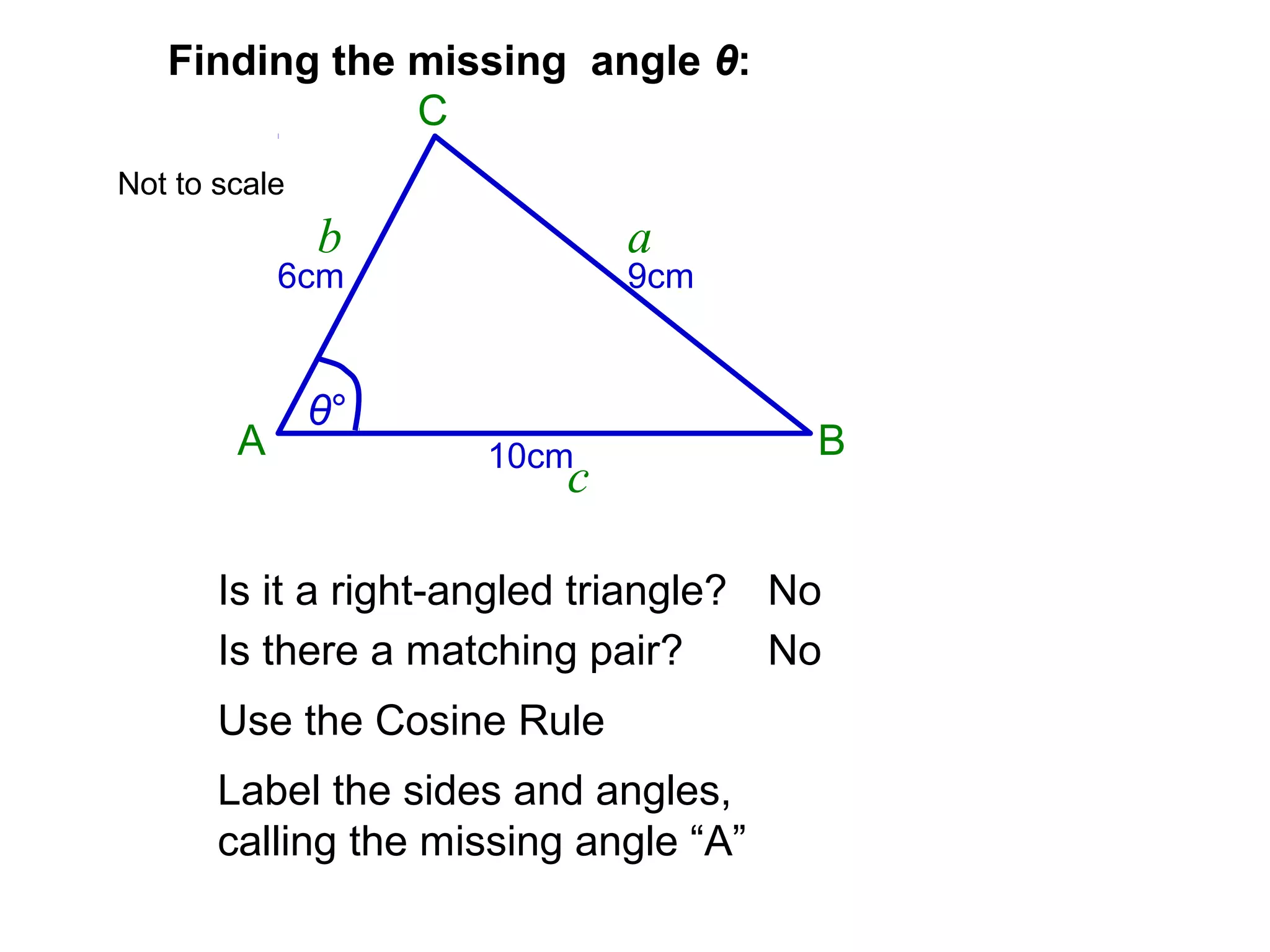
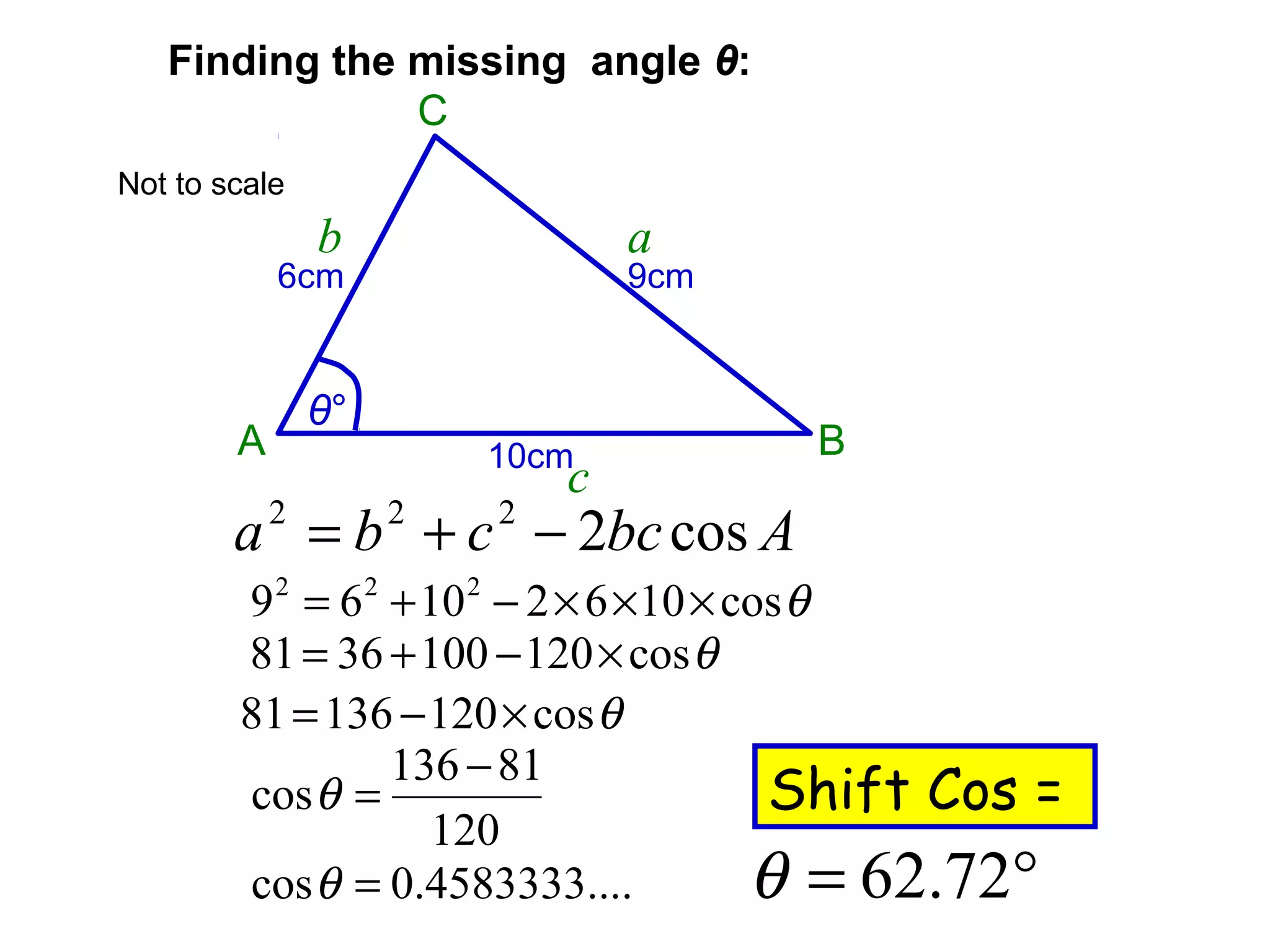
The document provides guidance on using trigonometric rules to solve problems involving sides and angles of triangles. It explains that the Sine Rule is used when there is a "matching pair" of a known side and its corresponding angle. The Cosine Rule is used when there is no right angle or matching pair. Examples are given of using both rules to calculate missing sides or angles of triangles.

2. If the question concerns lengths or angles in a triangle,
you may need the sine rule or the cosine rule.
First, decide if the triangle is right-angled.
Then, decide whether an angle is involved at all.
If it is a right-angled triangle, and there are angles
involved, you will need straightforward Trigonometry,
using Sin, Cos and Tan.
If the triangle is not right-angled, you may need the
Sine Rule or the Cosine Rule
If it is a right-angled triangle, and there are no angles
involved, you will need Pythagoras’ Theorem

3. In any triangle ABC
The Sine Rule:
A B
C
ab
c
C
c
B
b
A
a
sinsinsin
==
or
c
C
b
B
a
A sinsinsin
==
Not right-angled!

4. You do not have to learn the Sine Rule or the Cosine Rule!
They are always given to you at the front of the Exam Paper.
You just have to know when and how to use them!

5. The Sine Rule:
A B
C
ab
c
You can only use the Sine Rule if you have a “matching pair”.
You have to know one angle, and the side opposite it.

6. The Sine Rule:
A B
C
ab
c
You can only use the Sine Rule if you have a “matching pair”.
You have to know one angle, and the side opposite it.
Then if you have just one other side or angle, you can use
the Sine Rule to find any of the other angles or sides.

7. 10cm
x
65°
Finding the missing side:
Is it a right-angled triangle?
Is there a matching pair?
No
Yes
40°
Not to scale

8. 10cm
65°
Finding the missing side:
Is it a right-angled triangle?
Is there a matching pair?
No
Yes
Label the sides and angles.
A
B
C
a
b
c
40°
x
Use the Sine Rule
Not to scale

9. 10cm
65°
Finding the missing side:
A
B
C
a
b
c
40°
x
C
c
B
b
A
a
sinsinsin
==
We don’t need the “C” bit of the formula.
Because we are trying to find
a missing length of a side,
the little letters are on top
Not to scale

10. 10cm
65°
Finding the missing side:
A
B
C
a
b
c
40°
x
B
b
A
a
sinsin
=
Fill in the bits you know.
Because we are trying to find
a missing length of a side,
the little letters are on top
Not to scale

11. 10cm
65°
Finding the missing side:
A
B
C
a
b
c
40°
x
B
b
A
a
sinsin
=
Fill in the bits you know.
°
=
° 65sin
10
40sin
x
Not to scale

12. 10cm
65°
Finding the missing side:
A
B
C
a
b
c
40°
x
B
b
A
a
sinsin
=
°
=
° 65sin
10
40sin
x
°×
°
= 40sin
65sin
10
x
09.7=x cm
Not to scale

13. 10cm
7.1cm
65°
Finding the missing angle:
Is it a right-angled triangle?
Is there a matching pair?
No
Yes
θ°
Not to scale

14. Finding the missing angle:
Is it a right-angled triangle?
Is there a matching pair?
No
Yes
Label the sides and angles.
A
B
C
a
b
c
Use the Sine Rule
10cm
7.1cm
65°
θ°
Not to scale

15. Finding the missing angle:
We don’t need the “C” bit of the formula.
A
B
C
a
b
c
10cm
7.1cm
65°
θ°
Because we are trying to
find a missing angle, the
formula is the other way up.c
C
b
B
a
A sinsinsin
==
Not to scale

16. Finding the missing angle:
Fill in the bits you know.
Because we are trying to
find a missing angle, the
formula is the other way up.
A
B
C
a
b
c
10cm
7.1cm
65°
θ°
b
B
a
A sinsin
=
Not to scale

17. Finding the missing angle:
Fill in the bits you know.
10
65sin
1.7
sin °
=
θ
A
B
C
a
b
c
10cm
7.1cm
65°
θ°
b
B
a
A sinsin
=
Not to scale

18. Finding the missing angle:
1.7
10
65sin
sin ×
°
=θ
.....6434785.0sin =θ
A
B
C
a
b
c
10cm
7.1cm
72°
θ°
10
65sin
1.7
sin °
=
θ
°= 05.40θ
Shift Sin =
b
B
a
A sinsin
=
Not to scale

19. If the triangle is not right-angled, and there is not
a matching pair, you will need then Cosine Rule.
The Cosine Rule:
A B
C
ab
c
In any triangle ABC Abccba cos2222
−+=

20. Finding the missing side:
Is it a right-angled triangle?
Is there a matching pair?
No
No
9km
12cm
20°
A
C
B
x
Use the Cosine Rule
Label the sides and angles, calling the
given angle “A” and the missing side “a”.
a
b
c Not to scale

21. Finding the missing side:
9km
12cm
20°
A
C
B
x a
b
c
Fill in the bits you know.
Abccba cos2222
−+=
x = 4.69cm
°×××−+= 20cos9122912 222
a
)20cos9122(912 222
°×××−+=a
........026.22=a
69.4=a
Not to scale

22. Finding the missing side:
Is it a right-angled triangle?
Is there a matching pair?
No
No
8km
5km
130°
A man starts at the village of Chartham and walks
5 km due South to Aylesham. Then he walks
another 8 km on a bearing of 130° to Barham.
What is the direct distance between Chartham and
Barham, in a straight line?
A
C
B
First, draw a sketch.
Use the Cosine Rule
Not to scale

23. Finding the missing side:
a
8km
5km
130°
A man starts at the village of Chartham and walks
5 km due South to Aylesham. Then he walks
another 8 km to on a bearing of 130° to Barham.
What is the direct distance between Chartham and
Barham, in a straight line?
A
C
B
Abccba cos2222
−+=
Call the missing length you want to find “a”Label the other sides
b
c
a² = 5² + 8² - 2 x 5 x 8 x cos130°
a² = 25 + 64 - 80cos130°
a² = 140.42
a = 11.85 11.85km
Not to scale

24. Is it a right-angled triangle?
Is there a matching pair?
No
No
Use the Cosine Rule
a
9cm6cm
A
C
B
b
c10cm
θ°
Label the sides and angles,
calling the missing angle “A”
Finding the missing angle θ:
Not to scale

25. Finding the missing angle θ:
a
9cm6cm
A
C
B
b
c10cm
θ°
Abccba cos2222
−+=
θcos12013681 ×−=
θcos1201003681 ×−+=
θcos10621069 222
×××−+=
120
81136
cos
−
=θ
....4583333.0cos =θ
Shift Cos =
°= 72.62θ
Not to scale