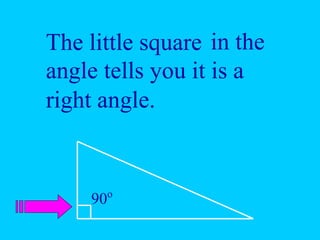
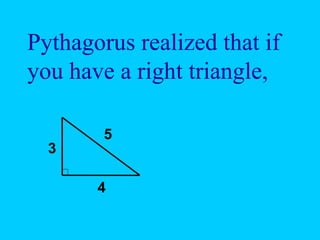
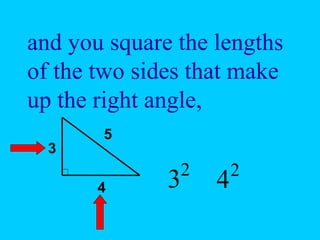
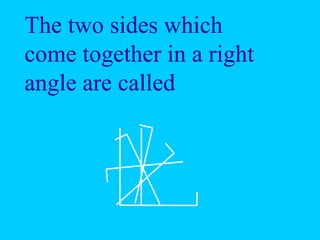
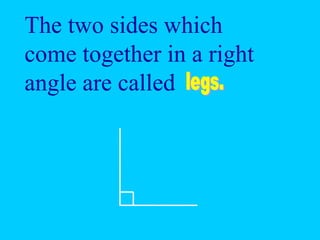
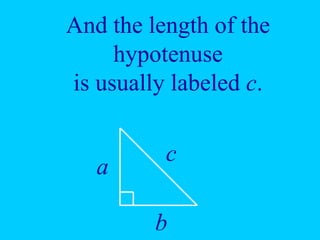
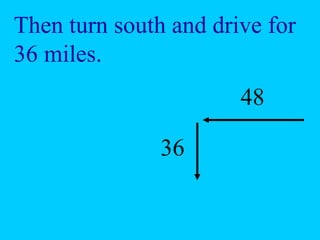
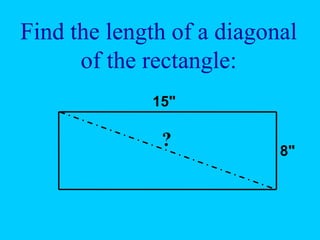
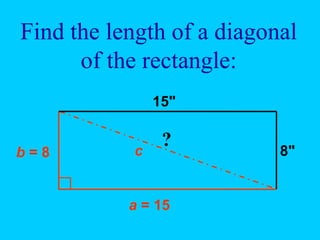
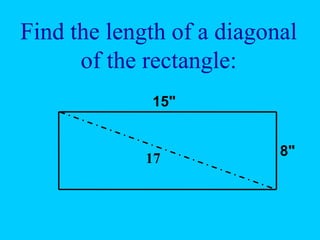
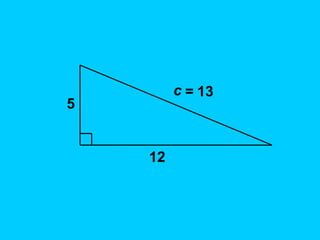
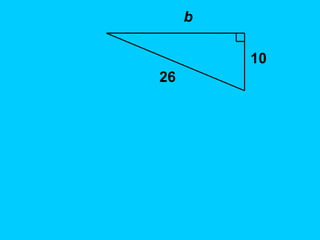
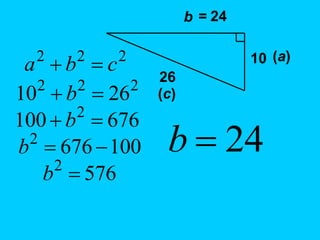
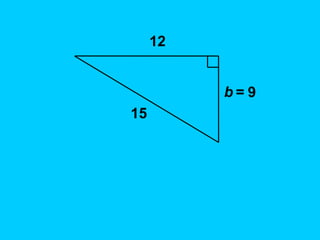
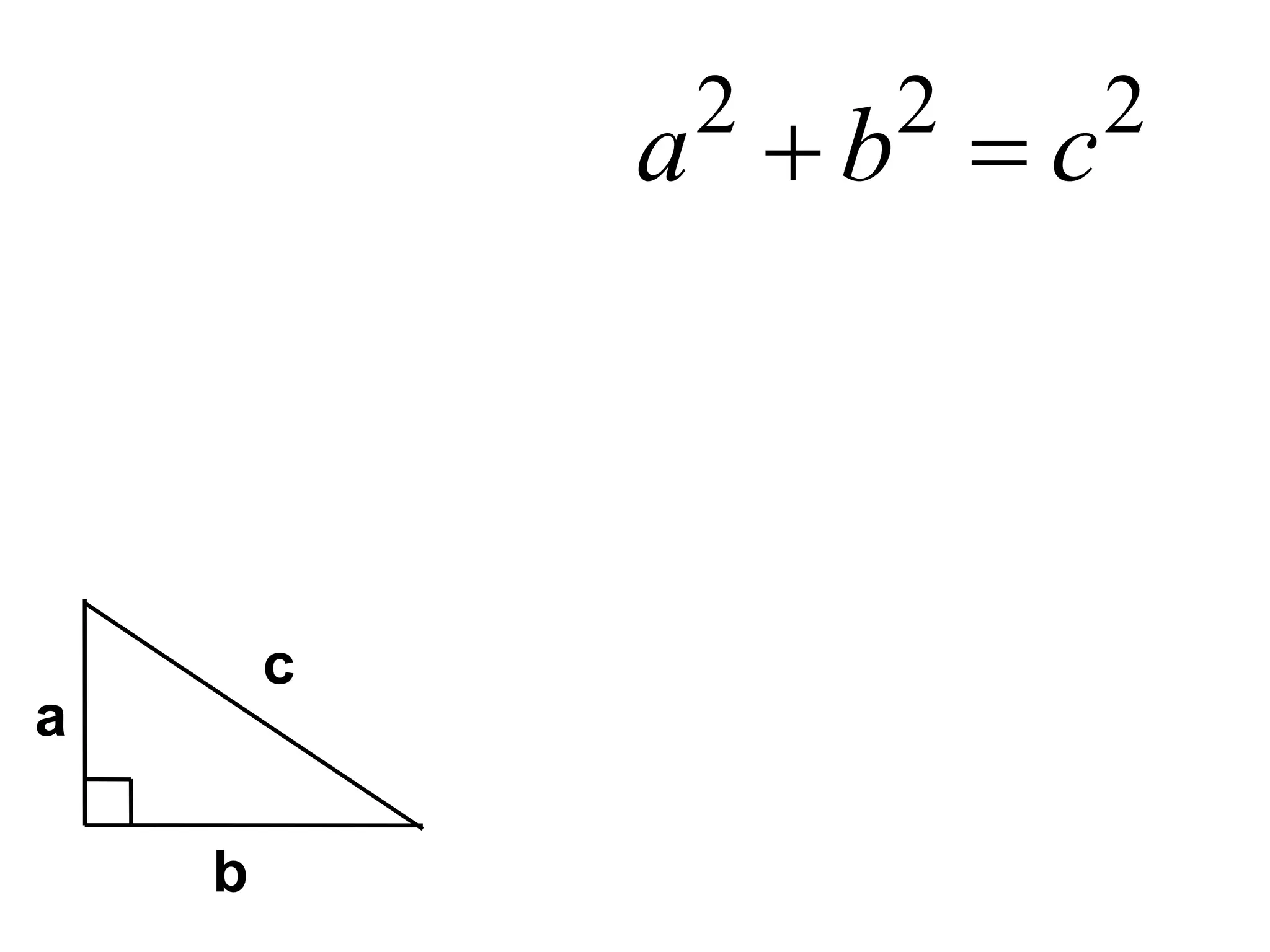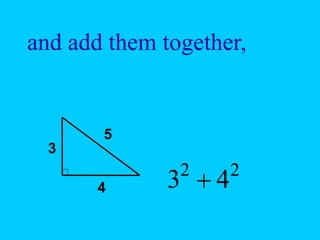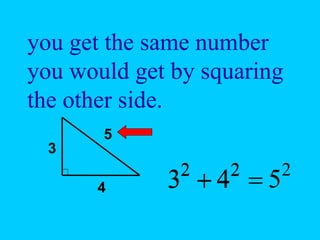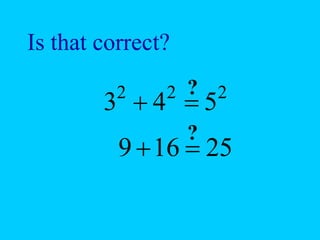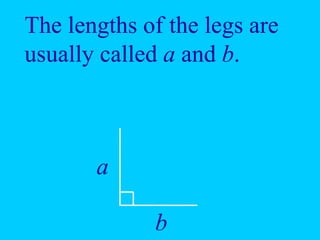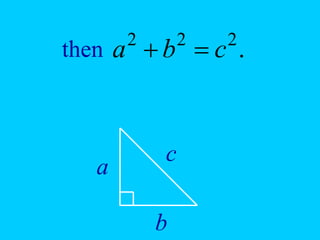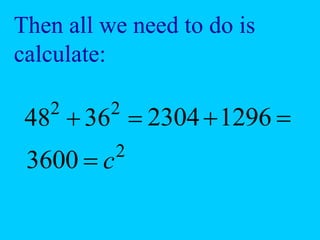The document explains the concept of right triangles and the Pythagorean theorem, which states that in a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. It provides examples of how to apply this theorem to find distances and includes informal proofs and practice problems related to right triangles. The document also discusses finding the height and area of an isosceles triangle using the Pythagorean theorem.

1. a
b
c
2
2
2
c
b
a 


2. This is a right triangle:

3. We call it a right triangle
because it contains a
right angle.

4. The measure of a right
angle is 90o
90o

5. The little square
90o
in the
angle tells you it is a
right angle.

6. About 2,500 years ago, a
Greek mathematician named
Pythagorus discovered a
special relationship between
the sides of right triangles.

7. Pythagorus realized that if
you have a right triangle,
3
4
5

8. and you square the lengths
of the two sides that make
up the right angle,
2
4
2
3
3
4
5

9. and add them together,
3
4
5
2
4
2
3 2
2
4
3 

10. 2
2
4
3 
you get the same number
you would get by squaring
the other side.
2
2
2
5
4
3 

3
4
5

11. Is that correct?
2
2
2
5
4
3 

?
25
16
9 

?

12. It is. And it is true for any
right triangle.
8
6
10
2
2
2
10
8
6 

100
64
36 


13. The two sides which
come together in a right
angle are called

14. The two sides which
come together in a right
angle are called

15. The two sides which
come together in a right
angle are called

16. The lengths of the legs are
usually called a and b.
a
b

17. The side across from the
right angle
a
b
is called the

18. And the length of the
hypotenuse
is usually labeled c.
a
b
c

19. The relationship Pythagorus
discovered is now called
The Pythagorean Theorem:
a
b
c

20. The Pythagorean Theorem
says, given the right triangle
with legs a and b and
hypotenuse c,
a
b
c

21. then
a
b
c
.
2
2
2
c
b
a 


22. You can use The Pythagorean
Theorem to solve many kinds
of problems.
Suppose you drive directly
west for 48 miles,
48

23. Then turn south and drive for
36 miles.
48
36

24. How far are you from where
you started?
48
36
?

25. 482
Using The Pythagorean
Theorem,
48
36
c
362
+ = c2

26. Why?
Can you see that we have a
right triangle?
48
36
c
482
362
+ = c2

27. Which side is the hypotenuse?
Which sides are the legs?
48
36
c
482
362
+ = c2

28. 
 2
2
36
48
Then all we need to do is
calculate:

1296
2304

3600 2
c

29. And you end up 60 miles from
where you started.
48
36
60
So, since c2
is 3600, c is 60.

30. PROVING THE PYTHAGOREAN THEOREM
• There are many proofs of the Pythagorean Theorem. An informal
proof is shown below. In the figure at the right, the four right
triangles are congruent, and they form a small square in the middle.
The area of the large square is equal to the area of the four triangles
plus the area of the smaller square.

31. Find the length of a diagonal
of the rectangle:
15"
8"
?

32. Find the length of a diagonal
of the rectangle:
15"
8"
?
b = 8
a = 15
c

33. 2
2
2
c
b
a 
 2
2
2
8
15 c


2
64
225 c

 289
2

c
17

c
b = 8
a = 15
c

34. Find the length of a diagonal
of the rectangle:
15"
8"
17

35. Practice using
The Pythagorean Theorem
to solve these right triangles:

36. 5
12
c = 13

37. 10
b
26

38. 10
b
26
= 24
(a)
(c)
2
2
2
c
b
a 

2
2
2
26
10 
 b
676
100 2

 b
100
676
2


b
576
2

b
24

b

39. 12
b
15
= 9

40. Find the area of the isosceles triangle with
side lengths 10 meters, 13 meters, and 13
meters.
• Solution
• STEP 1: Draw a sketch. The length of an altitude is the height of a
triangle. In an isosceles triangle, the altitude to the base is also a
perpendicular bisector. So, the altitude divides the triangle into two
right triangles with the dimensions shown.
• STEP 2: Use the Pythagorean Theorem to find the height of the
triangle.

41. Find the area of the isosceles triangle with
side lengths 10 meters, 13 meters, and 13
meters.
• Solution
•

42. Find the length of a hypotenuse using two
methods
• Solution
• Method 1: Use a Pythagorean triple. A common Pythagorean triple is
5, 12, 13. Notice that if you multiply the lengths of the legs of the
Pythagorean triple by 2, you get the lengths of the legs of this
triangle: 5* 2 = 10 and 12 *2 = 24. So, the length of the hypotenuse is
13 * 2 = 26.
• Method 2: Use the Pythagorean Theorem.